基于无源性的无刷直流电动机速度控制

谭传接，杨向宇，赵世伟

(华南理工大学，广州 510640)



基于无源性的无刷直流电动机速度控制

谭传接，杨向宇，赵世伟

(华南理工大学，广州 510640)

采用一种基于无源性控制算法对无刷直流电动机进行速度控制。利用电机的电压方程、电磁转矩方程和运动方程，推导出基于电机状态误差变量的能量函数，并针对实际运行过程中电机存在负载扰动问题，引入负载扰动观测器，通过设计合适的控制律，使得电机状态误差变量的能量函数能收敛于期望值。仿真与实验结果表明，该控制算法对无刷直流电动机速度控制具有控制简单、鲁棒性较好和稳态性能良好等优点。

无刷直流电动机；无源性控制；速度控制；负载观测器

0 引 言

无刷直流电动机(以下简称BLDCM)是从传统的有刷直流电动机发展而来的。它既保留了直流电机的机械特性，又通过安装电子换相装置取代直流电机的电刷和换向器，解决了直流电机换相火花的问题，提高了电机运行可靠性。BLDCM具有本体结构简单、体积小、功率密度大、噪声小、运行可靠等一系列优点，适用于航空航天、电动车、电脑外设和家用电器等领域[1]。

BLDCM是一个多变量、非线性的控制系统，采用传统的PID调节器虽然能达到较好的控制效果，但PID调节器对电机运行工况适应性差，控制效果难以保证[2]。文献[3]采用模糊遗传算法优化对BLDCM进行控制，虽然系统很好地对预设速度参考模型的跟踪，具有较好的鲁棒性，但算法比较复杂。无源性控制是一种非线性控制方法，它通过寻找与被控对象状态相关的能量函数，设计无源性控制律，使得系统状态变量能渐进收敛至期望值，从而达到控制的目的[4]。文献[5-7]分别研究了无源性控制算法在直线开关磁阻电机、鼠笼式感应电机和无刷双馈电机的应用，控制算法具有全局稳定性，实现了电机的转速控制。

本文在分析BLDCM数学模型的基础上，将无源性控制算法应用于BLDCM速度控制系统，并通过设计负载观测器来抑制电机负载扰动对电机速度的影响，以提高系统的速度控制效果与鲁棒性。最后在MATLAB/Simulink环境进行BLDCM速度控制系统仿真，并通过实验验证无源性控制算法对电机速度的控制效果。

1 BLDCM数学模型

为得到BLDCM的电压方程，电磁转矩方程和运动方程。根据BLDCM的结构原理，进行以下假设：电机具有三相完全对称，空间上互差120°的定子绕组；电机具有梯形波的三相绕组反电动势；电机三相绕组的电感、电阻参数一致；电机具有均匀的气隙磁导，磁路不饱和 。

BLDCM的电压方程可表示：

(1)

式中:ua,ub,uc为电机的对参考地电压；ia,ib,ic为电机的相电流；Ra,Rb,Rc为相电阻；Laa,Lbb,Lcc为相自感；Lab,Lac,Lba,Lbc,Lca,Lcb为相互感；ea,eb,ec为相电动势；un为电机三相绕组中点对参考地电压；p为微分算子。

由于电机定子绕组采用三相星形接法，并采用两两导通的控制方式，则有ia+ib+ic=0，由电机建模的假设条件，有Ra=Rb=Rc=R，Laa=Lbb=Lcc=L1，Lab=Lac=Lba=Lbc=Lca=Lcb=M，记电机三相绕组中点电压为参考地电压，反电动势大小为e，正常换相导通时，有:

(2)

式中:Cj(j=a，b，c)为电机相反电动势系数。将式(2)代入式(1)可得电压方程：

(3)

式中:L为等效相电感，L=L1-M。

BLDCM的等效电路图如图1所示。

图1 BLDCM的等效电路

BLDCM的电磁转矩方程：

(4)

式中:Te为电机的电磁转矩。

将式(2)代入式(4)可得电机转矩方程如下：

(5)

BLDCM的运动方程：

(6)

式中:B为摩擦系数;J为电机的转动惯量;ω为电机角速度;TL为负载转矩。

2 无源性控制器设计

选择BLDCM的三相电流和角速度作为状态变量，则电机状态变量表示为XT=[iaibicω]，结合式(3)、式(5)、式(6)，可得电机状态方程：

(7)

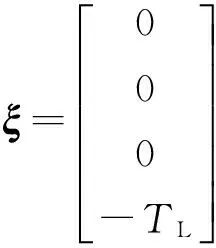
定义状态误差向量为E=X-Xd，其中Xd为系统状态变量参考值。将状态误差代入式(7)中，可以得到电机状态变量误差方程：

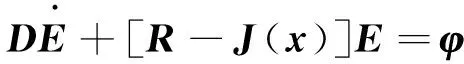
(8)

其中:

(9)

取电机状态误差的能量函数:

(10)

状态变量误差函数对时间的导数可以表示为下式：

(11)

由式(8)和式(11)可得：

(12)

由于J(x)是一个反对称矩阵，所以ETJ(x)E=0；由式(12)可表示：

(13)

根据Lyapunov稳定性判别定理，如果可以保证H(·)(E)在其平衡点处取得零值和在状态域的其他点上具有负值，那么状态误差函数H(E)将会耗散到零，而状态变量将趋近期望值。通过设定合适的控制律，使等式(14)成立:

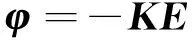
(14)

其中，K=diag(k1,k2,k3,k4)，K为正定的四阶对角矩阵，代入式(13)可得：

(15)

由式(9)和式(14)可以得到：

(16)

式(16)就是控制器所要求解的控制律。它具有全局稳定性，在负载扰动已知的情况下，能保证系统状态变量达到期望值。

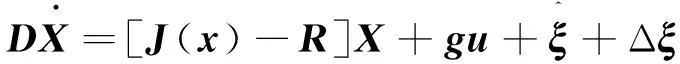
(17)

ξ(＾)为系统观测到的扰动向量，Δξ为系统实际扰动与观测扰动之差。

其误差状态方程可表示如下：

(18)

记:

(19)

将其代入式(18)可得：

(20)

那么构造关于负载扰动未知的系统状态误差能量函数如下：

(21)

式中：k为一个正数。

此时系统状态误差函数对时间的导数表示：

(22)

为保证在电机参数摄动和负载扰动下保持稳定，可以将控制器设计:

(23)

(24)

将状态误差向量E和扰动偏差向量Δξ代入式(24)可得:

(25)

(26)

为计算方便，对控制参数进行简化，可以记k1=k2=k3=ki，k4=kw，结合式(19)，式(23)，式(26)可得：

(27)

由于电机采用两两导通方式，电机处于两相导通，第三相悬空的状态，导通两相电流大小相等，方向相反，悬空相电流为零，所以只需要观测到电机的速度和导通相的电流就可以对电机进行控制。

此时，记电机电流参考值为id，实际电流大小为i，那么导通的两相电流参考值电流应取id与-id，实际电流为i和-i，相反电势系数分别为Ce和-Ce；悬空相电流参考值为零，电流实际值也为零，其反电势系数是一个与转子位置相关的量。设电机端电压为u，那么根据式(27)无源性控制律可表示如下：

(28)

3 电机仿真与实验结果

为验证文中的无源性控制算法的控制效果，在MATLAB/Simulink平台上搭建BLDCM的仿真模型。BLDCM的参数如下：极对数为4，等效电感L=2.565 mH，等效电阻R=0.5 Ω，转动惯量为J=0.000 25 kg·m2，阻尼系数B=0.000 03 N·rad·s-1。其额定电压为24 V，额定转速为3 000 r/min。仿真过程中，设定的转速n=2 000 r/min，在0到0.3 s时，电机空载运行，在0.3 s时对电机施加一个负载转矩TL=0.1 N·m，可以得到电机的转速变化曲线如图2所示。图3为电机0.3 s时的转速仿真局部放大图。

由图2可以看出，无源性控制和PID控制都可以准确地跟踪电机的转速指令，但无源性控制在电机启动时，能较快地达到设定转速，没有超调量，而PID控制会有较大的超调量；并且在0.3 s时刻电机受到突加负载转矩的作用，电机转速出现下降，从图3电机转速局部仿真图中，可以明显看到电机在无源性控制算法下，转速下降较小，并能较快地恢复到设定转速，而在PID控制算法下，转速下降较大，对负载扰动较为敏感。仿真结果表明，无源性控制能保证系统的稳定运行，较好地跟踪电机的转速，实现对电机的转速控制。

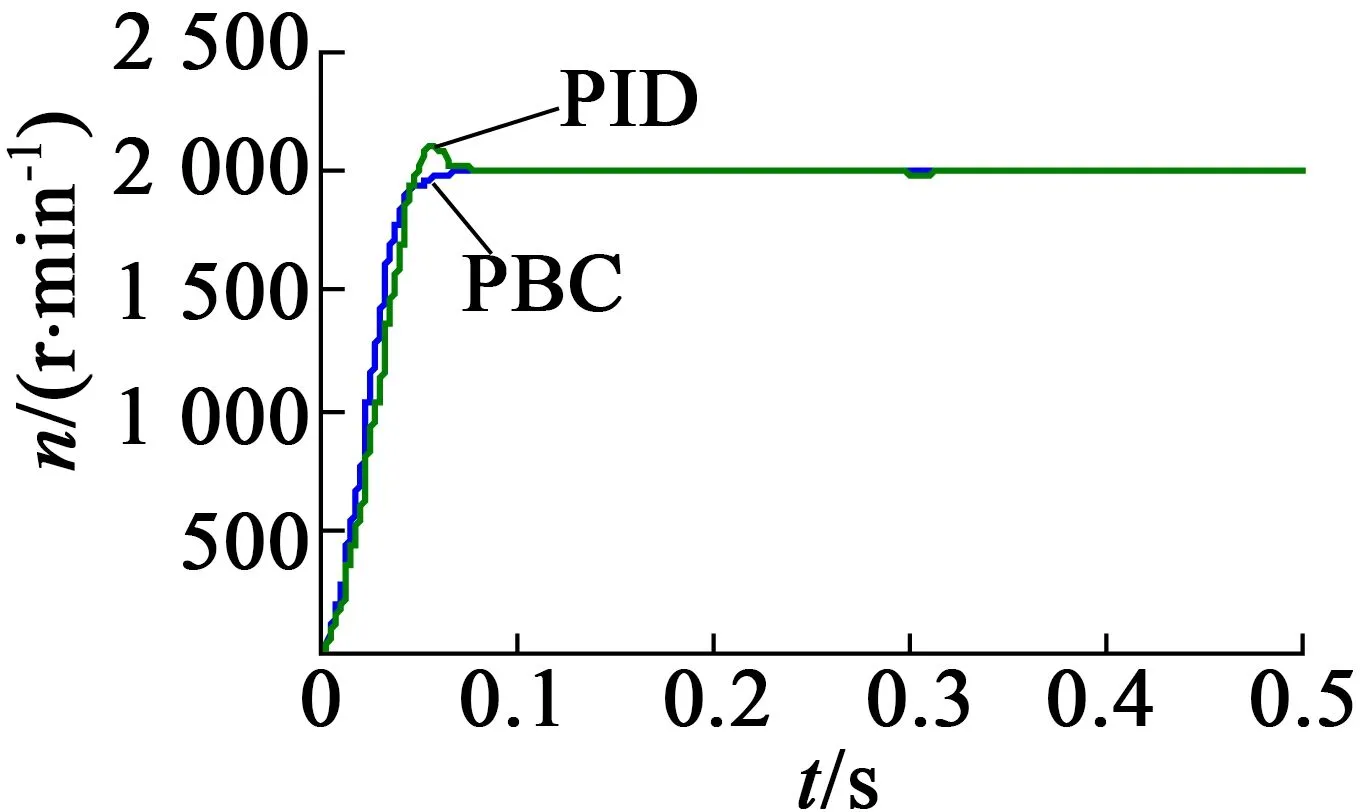
图2 电机转速仿真

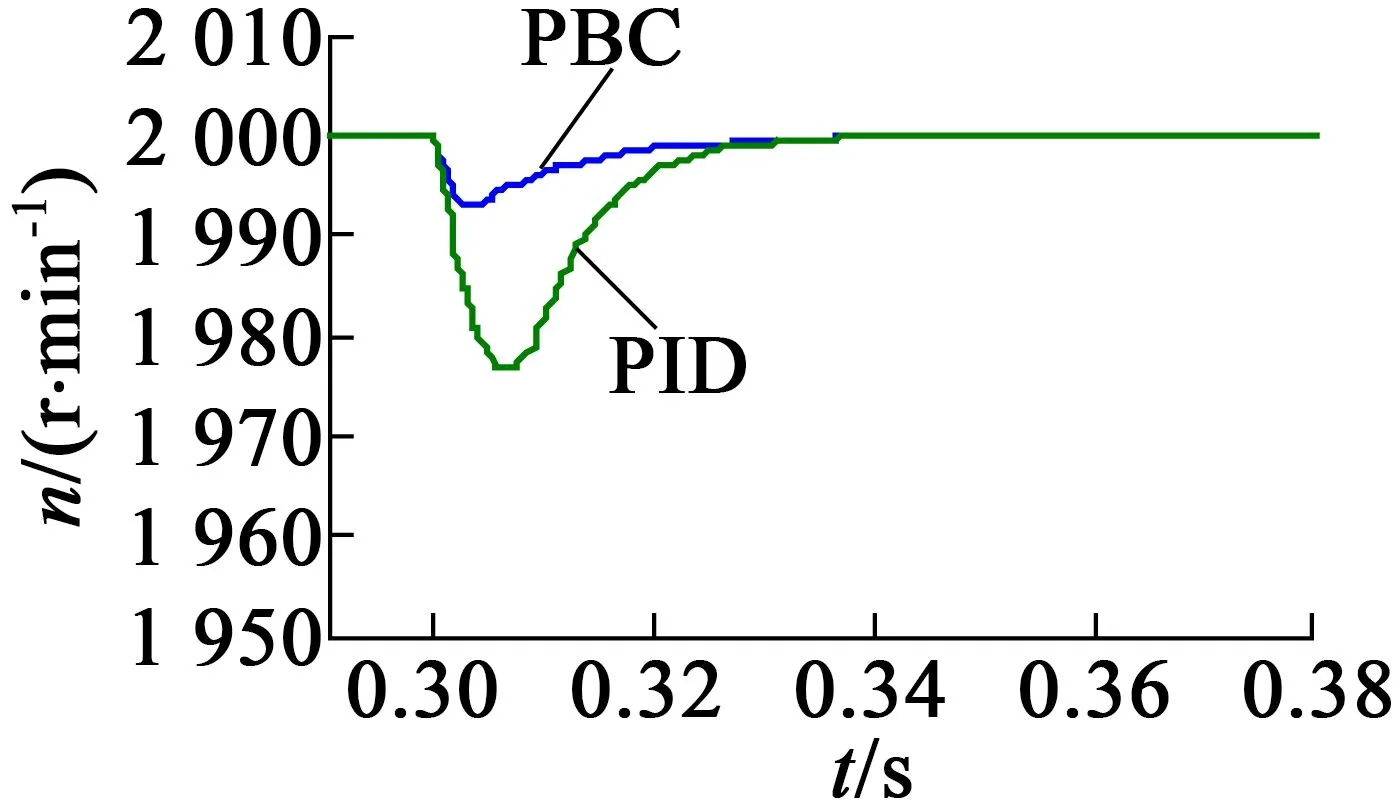
图3 电机转速仿真(局部)

本文通过dsPIC33芯片搭建的BLDCM控制系统对无源性控制算法进行验证。电机控制系统由dsPIC控制器，三相驱动电路，检测电路和BLDCM四部分构成。其结构如图4所示。

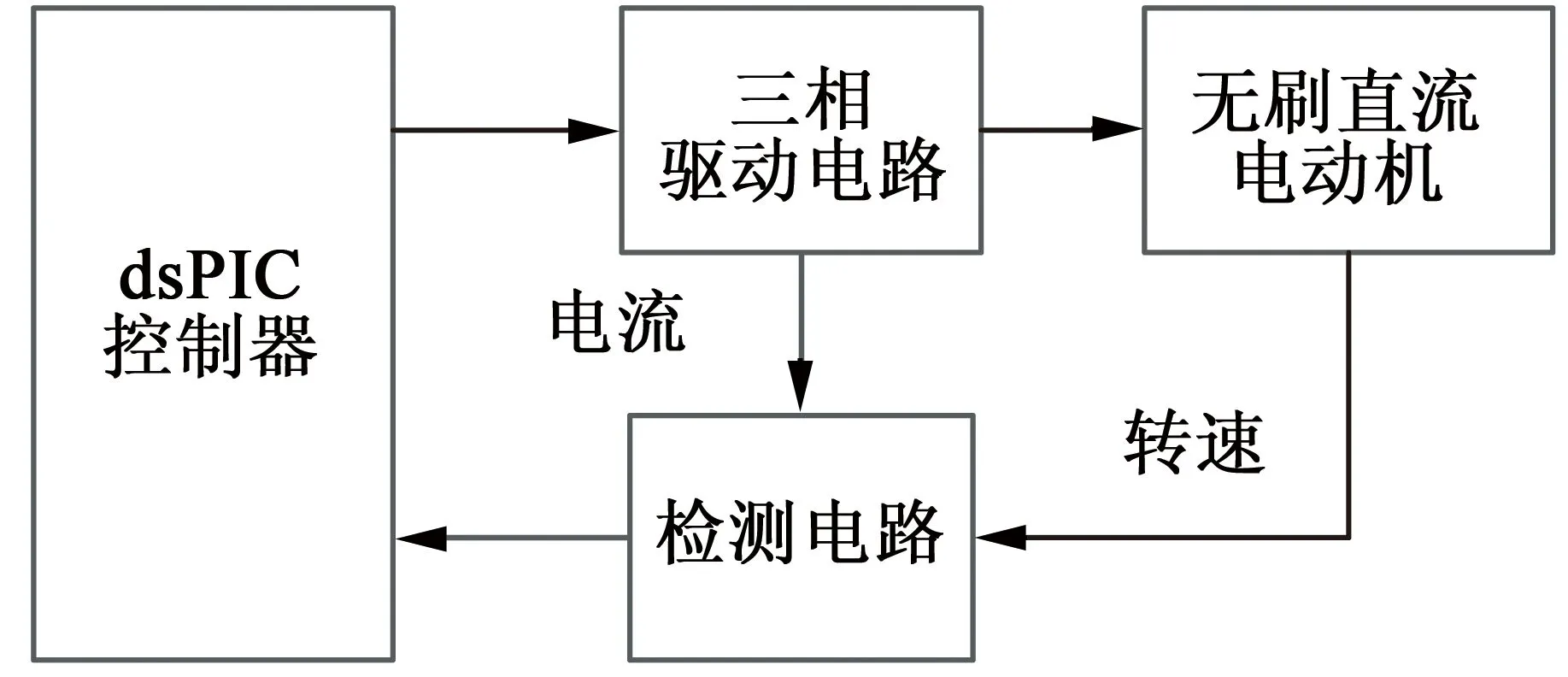
图4 电机控制系统结构图

在给定转速n=2 000 r/min的条件下，分别得到BLDCM PID控制和无源性控制的转速响应，如图5和图6所示。从两者的转速响应图可以看出，无源性控制和PID控制都能稳定跟踪系统设定的转速，基本实现无稳态误差。同时，无源性控制比PID控制有较短的响应时间，且电机转速没有超调。

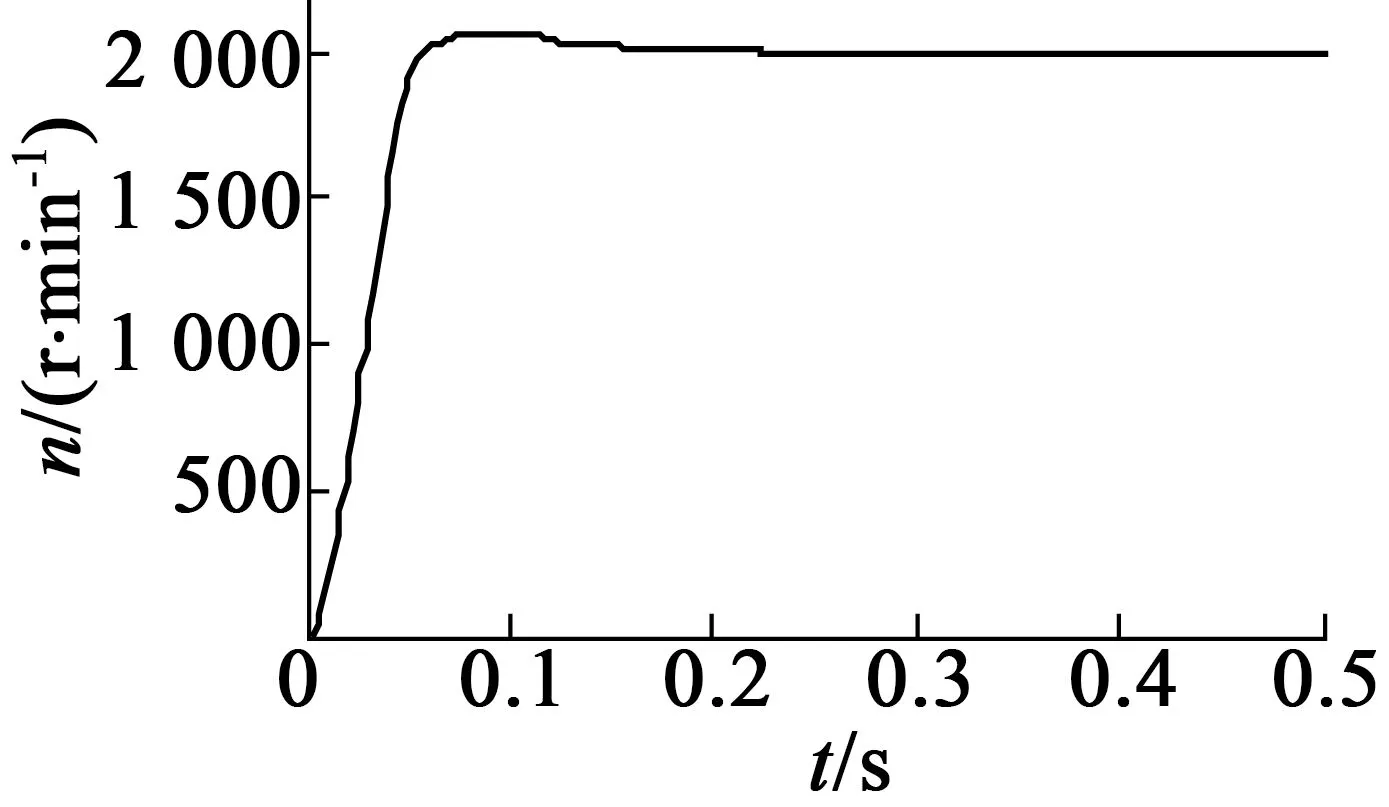
图5 PID控制的电机转速响应

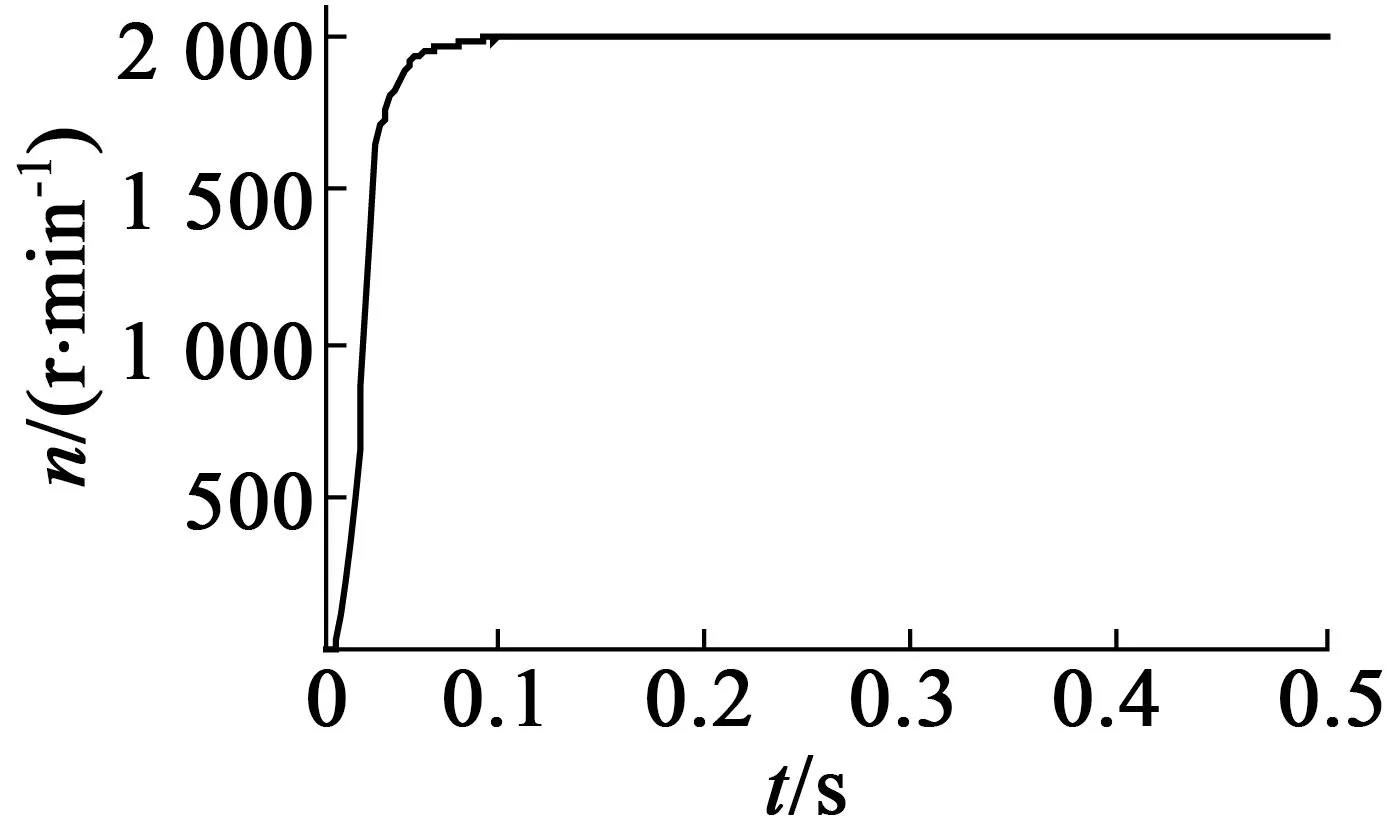
图6 无源性控制的电机转速响应

实验结果表明，无源性控制算法能很好地跟踪电机的转速指令，其响应速度快，稳态误差小。

4 结 语

无源性算法是一种非线性控制算法，它从系统状态误差的能量耗散去分析系统的稳定性，保证系统有全局稳定性。本文通过设计BLDCM进行无源性控制算法，并针对电机在实际运行过程中存在外加负载扰动的情况进行分析，采用负载扰动观测器来提高控制系统的鲁棒性。仿真与实验证明，无源性控制器能很好地跟踪电机设定转速和较快的动态响应性能，对电机的负载扰动具有较强的鲁棒性。

[1] 刘刚,王志强,房建成.永磁无刷直流电机控制技术与应用[M].北京:机械工业出版社,2008.

[2] 刘海珊,陈宇晨.无刷直流电动机PID控制系统仿真及实验研究[J].系统仿真学报,2009,21(16):5157-5160.

[3] 夏长亮,郭培建,史婷娜,等.基于模糊遗传算法的无刷直流电机自适应控制[J].中国电机工程学报,2005,25(11):129-133.

[4]NICKLASSONPJ,ORTEGAR,ESPINOSAPG,etal.Passivity-basedcontrolofaclassofBlondel-Parktransformableelectricmachines[J].IEEETransactionsonAutomaticControl,1997,42(5):629-647.

[5]ZHAOSW,CHEUNGNC,GANWC,etal.Passivity-basedcontroloflinearswitchedreluctancemotorswithrobustnessconsideration[J].ElectricPowerApplications,IET,2008,2(3):164-171.

[6] 廖冬初,陈力.鼠笼式感应电动机无源性转速控制系统[J].微特电机,2013,41(5):1-3,8.

[7] 韩力,潘红广.无刷双馈电机转矩和转速的无源性控制[J].电机与控制学报,2011,15(11):1-6.

Passive Based Speed Control for Brushless DC Motor

TANChuan-jie，YANGXiang-yu，ZHAOShi-wei

(South China University of Technology,Guangzhou 510640,China)

To improve the speed control performance of brushless DC motor, a speed control algorithm based on passivity theory was applied. The passivity of the control system of Brushless DC motor was analyzed, with the voltage equation, torque equation and motion equation of brushless DC motor. In order to improve the performance of the controller, a load disturbance observer was designed for compensating unknown load disturbances. A suitable control law can make the variables of the motor state error energy function converge to the desired value. Simulation and experiment show that the passive control has the advantages of simple control, good robustness and good performance for brushless DC motor.

brushless DC motor； passive based control； speed control； load observer

2016-03-02

TM33

A

1004-7018(2016)08-0122-04

谭传接(1990-)，男，硕士研究生，研究方向为电气传动及其智能控制。