双相励磁8/6极开关磁阻电动机转矩数学模型
李 波,肖林京,孙传余,文艺成,肖 楠,陈忠霞
(山东科技大学,青岛 266590)
双相励磁8/6极开关磁阻电动机转矩数学模型
李 波,肖林京,孙传余,文艺成,肖 楠,陈忠霞
(山东科技大学,青岛 266590)
为研究双相励磁8/6极开关磁阻电动机转矩特性,文章根据电机原理和等效磁路法,给出了双绕组间自感、互感公式;利用开关磁阻电动机磁路分割法,求解了8/6极开关磁阻电动机的气隙磁导,进而推导出电机的转矩模型公式。最后,通过有限元仿真结果,证明了转矩数学模型的正确性。研究表明:该转矩数学模型能正确描述8/6极开关磁阻电动机无位置偏移时的转矩输出特性。
开关磁阻电动机;双相励磁;数学模型;有限元分析
0 引 言
开关磁阻电动机[1-2](以下简称SRM),作为一种新型电机,因结构简单、工作可靠、维护量小、启动性能及调速性能优越等优点,受到了研究学者的广泛关注。
8/6极SRM从励磁方式可分为单相励磁和双相励磁,文献[3-4]针对上述两种不同的励磁方式,对其自感、互感及转矩输出特性进行了理论及实验分析,研究表明双相励磁模式较单相励磁模式,具有平均转矩高、输出平稳性好的优点。
转矩性能是SRM领域的研究重点,对SRM调节转速、稳定旋转等具有重要意义,文献[5]针对8/6极SRM,在建立样机仿真模型,获取并分析仿真数据的基础上,给出了自互感模型、磁链模型以及转矩模型,但上述模型为基于该样机仿真数据的拟合模型,并未给出关于电机具体参数的数学公式。文献[6]针对8/6极单绕组磁悬浮SRM,借鉴文献[7-10]的磁路分割法,通过建立等效磁路模型、求解气隙磁导,推导出了电机转矩模型。由于8/6极磁悬浮SRM和8/6极SRM具有相同的定转子齿极结构,即而借鉴8/6极磁悬浮SRM的气隙磁导求解方法,并应用到8/6极SRM气隙磁导的计算研究中。
文章针对双相励磁8/6极SRM,在Maxwell 2D仿真分析的基础上,建立了等效磁路模型,并推导出自互感表达式;再利用磁路分割法给出了齿间气隙磁导求解方法及磁导公式,藉此推导出双相励磁8/6极SRM的转矩数学模型;最后通过有限元仿真对比,验证了该数学模型的正确性。
1 SRM原理
双相励磁8/6极SRM,包括电机定子、电机转子和励磁绕组,且两相绕组共同通电,为电机转子提供电磁吸引力。如图1所示,AB相励磁绕组通电后,在定转子齿间形成电磁通路,产生电磁吸引力,驱动电机转子逆时针转动。
定义逆时针旋转方向为正,定转子齿极正对时,转子位置角为0,则AB相导通时,A相转子位置角θa∈[-π/12,0],B相转子位置角θb∈[-π/6,-π/12],D相转子位置角θd∈[0,π/12],且有关系θb=θa-π/12,θd=θa+π/12,图1中所示为θa=-π/24的位置。

图1 双相励磁8/6极SRM原理图
2 SRM有限元分析
本文采用Maxwell 2D有限元仿真软件,建立双相励磁8/6极SRM的二维模型,选择材料,定义边界条件,添加绕组激励,设置运动参量,最后完成瞬态磁场的仿真分析。其中,二维电机模型参数设置如下:定子铁心外半径30 mm,内半径19.1 mm,定子轭环厚度4.9 mm,定子齿极高6 mm,定子齿极宽7.45 mm;转子铁心外半径19 mm,内半径5.36 mm,转子轭环厚度5 mm,转子齿极高8.64 mm,转子齿极宽7.41 mm;轴向长度1 000 mm,各相绕组匝数50。
Maxwell 2D针对双相励磁8/6极SRM,进行磁路仿真分析,当AB相绕组导通且 时,其磁路与磁密分布分别如图2、图3所示。

图2 电机磁路分布图图3 电机磁密分布图
由图2知,AB相绕组磁力线主要经由AB相相邻定转子齿极及AD相相邻定转子齿极,形成闭合磁路,少量磁力线经由AB相相对定转子齿极和AC相定转子齿极,形成闭合磁路。
由图3知,AB相磁力线主要集中于A相、B相、D相定转子齿极处,极少量分布在C相定转子齿极处。且仿真发现,随着θa减小,C相定转子齿极处磁密会有所增加,但相较于A相、B相、D相仍可忽略不计。
3 SRM转矩数学模型
为简化双相励磁8/6极SRM转矩求解,忽略漏磁通、定子交链转子轭部磁通、磁钢磁导和磁路饱和现象,并假设SRM电机转子处于平衡位置。
以8/6极SRM的AB相绕组励磁为例,认为AB相通电过程中,磁力线仅经由A、B、D三相支路导通,即忽略C相定转子齿间气隙磁导,并绘制其等效磁路图,如图4所示:Na为A相绕组匝数;ia为A相绕组电流;Nb为B相绕组匝数;ib为B相绕组电流;Pa1,Pa2和φa1,φa2分别为A相上、下两个气隙处的气隙磁导和气隙磁通量;Pb1,Pb2和φb1,φb2分别为B相上、下两个气隙处的气隙磁导和气隙磁通量;Pd1,Pd2与φd1,φd2分别为D相上、下两个气隙处的气隙磁导和气隙磁通量。
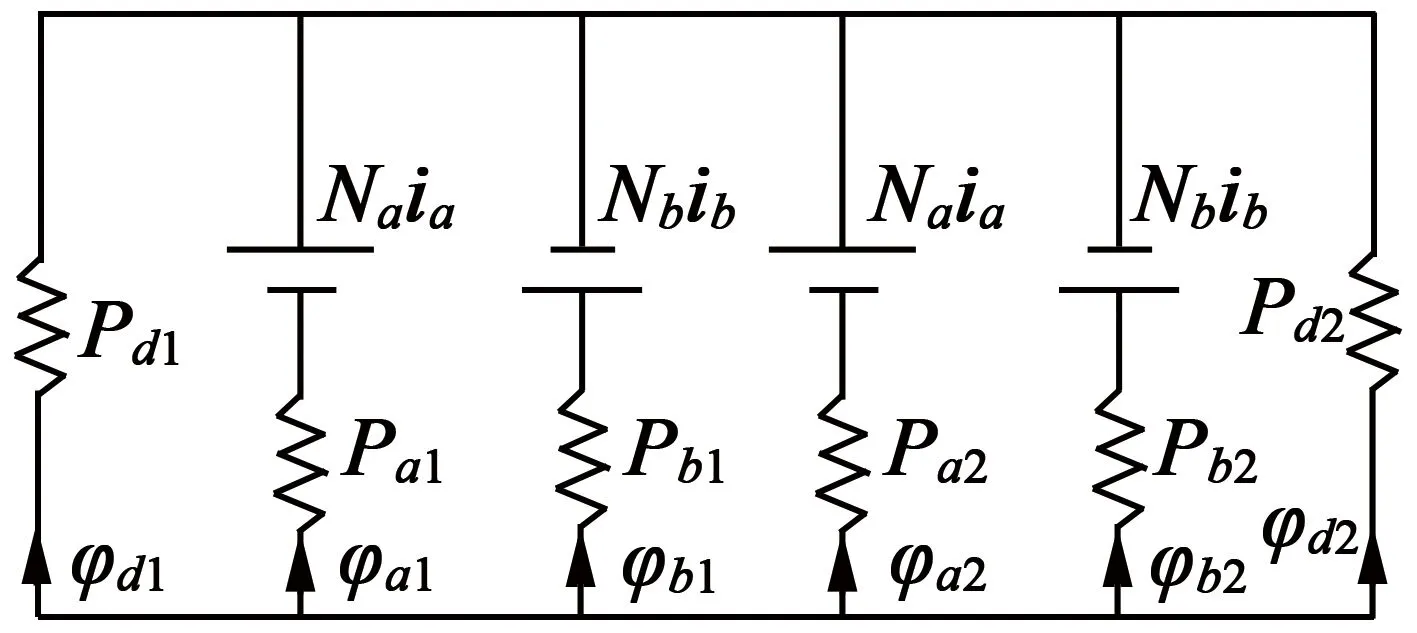
图4 AB相等效磁路图
由电机齿极结构的对称性,可知Pa1=Pa2,Pb1=Pb2,Pd1=Pd2,且φa1=φa2,φb1=φb2,φd1=φd2,根据AB相等效磁路图,可得AB相绕组自感、互感表达式:
(1)
式中:La为A相绕组自感;Lb为B相绕组自感;Mab为AB相绕组互感;P0=Pa+Pb+Pd;Pa=Pa1=Pa2;Pb=Pb1=Pb2;Pd=Pd1=Pd2。
根据文献[6-10],求解气隙磁导时,利用磁路分割法,将齿间磁路分割为正对部分的直线磁路和非正对部分的椭圆磁路。

图5 磁路分割图
当SRM转子无位置偏移时,其气隙磁导[6]:
(2)
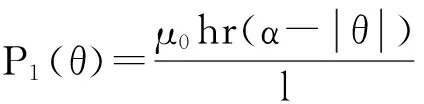
根据双相励磁8/6极SRM原理可知,A相转子位置角θa∈[-π/12,0],带入式(2),得A相齿间气隙磁导Pa:
(3)
同理可知,D相转子位置角θd∈[0,π/12],且有θd=θa+π/12,则D相齿间气隙磁导Pd:
(4)
对于B相齿间气隙磁导 ,已知其转子位置角θb∈[-π/6,-π/12],且θb=θa-π/12。如图1所示,当θb∈[-π/8,-π/12](即θa∈[-π/24,0])时,B相定转子齿极既有正对部分,又有非正对部分,与A、B相同理求解,即有:
(5)
当θb∈[-π/6,-π/8](即θa∈[-π/12,-π/24])时,B相转子齿与B相定子齿完全偏离,仅有非正对部分气隙磁导,如图6所示,此时气隙磁导式(2)不再适用,Pb求解方式如下。
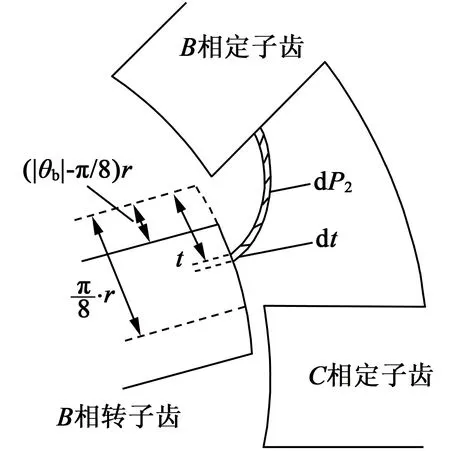
图6 B相气隙磁路示意图
根据文献[7],非正对部分微元磁导公式:
(6)
式中:dP2为非正对部分微元磁导;dt为非正对部分微元长度。
首先假设:(1) B相转子齿与B相定子齿完全偏离时,非正对部分微元磁导仍符合式(6);(2) 忽略B相转子齿与C相定子齿间的气隙磁导。根据图6可知,非正对部分微元磁导dP2的积分长度t∈[(|θb|-π/8)r,π/8·r]。
将积分长度上下限,带入式(6),并化简得:
(7)
整合式(5)和式(7),得:
(8)
已知双相励磁8/6极SRM,AB相绕组储能式Wab:
(9)
得双相励磁8/6极SRM转矩公式T(θa):
(10)
联立式(1)、式(3)、式(4)、式(8)、式(10),并化简,得电机转矩数学模型:
(11)
式中:
f0=fa+fb+fd。
4 仿 真
以双相励磁8/6极SRM为仿真对象,利用Maxwell2D有限元仿真软件,得到θa∈[-15°,0°]过程中,电机转矩与θa间的仿真输出转矩曲线。另,依据转矩数学模型式(11),利用MATLAB软件,绘制转矩T(θa)与θa间的模型计算转矩曲线。通过对比仿真输出转矩与模型计算转矩的拟合效果,验证转矩数学模型的正确性。
双相励磁8/6极SRM仿真模型,分别设定AB相励磁绕组电流ia=ib=2A,ia=ib=3A,进行瞬态仿真,则仿真输出转矩与模型计算转矩的对比情况如图7所示。由图7对比可知,仿真输出转矩与模型计算转矩拟合效果良好,即转矩数学模型式(11)能较准确地描述双相励磁8/6极SRM导通周期内的转矩输出情况。

图7 仿真输出转矩与模型计算转矩对比图
但曲线绘制过程中发现,模型计算转矩曲线为非连续曲线,间断点为[-7.5°,T(-7.5°)],原因在于:气隙磁导Pb在θa=-7.5°处,连续不可导,而转矩T(θa)求解时,需对Pb求导,继而导致了转矩T(θa)在该点处不连续。由图7中亦可看出,由间断采样数据绘制出的模型计算转矩曲线在[-7.5°,T(-7.5°)]点处并不圆滑。
5 结 语
文章通过研究双相励磁8/6极SRM转矩数学模型,得出如下结论:
(1) 转矩数学模型式(11)能较准确地描述双相励磁8/6极开关磁阻电机的转矩输出情况;(2) 式(11)为非连续函数,间断点为[-7.5°,T(-7.5°)],由此导致,当转子位置角θa趋近于-7.5°时,实际输出转矩与公式计算可能存在一定偏差。
[1] 吴建华.开关磁阻电机设计与应用[M].北京:机械工业出版社,2000.
[2] 甘醇,吴建华,王宁,等.一种零电压保持开通的开关磁阻电机再生制动控制策略[J].电机与控制学报,2015,19(9):8-15.
[3] 高洁,张鹤旭,米彦青.计及互感的开关磁阻电机单双相励磁静态性能分析[J].电机与控制学报,2012,16(11):45-51.
[4] 弓锵,曲尔光,刘艳芳.8/6极开关磁阻电机两相励磁电磁转矩分析[J].现代电子技术,2012,35(12):176-178.
[5] 林委.计及互感的8/6极开关磁阻电机转矩估算模型研究[D].重庆:重庆大学,2014.
[6] 嵇小辅,马滔,项倩雯.8/6极单绕组磁悬浮开关磁阻电机建模与分析[J].微电机,2014,47(6):9-14.
[7] TAKEMOTO M,SUZUKI H,CHIBA A,et al.Improved analysis of a bearingless switched reluctance motor[J].IEEE Transactions on Industry Applications,2001,37(1):26-34.
[8] 张京军,龙荣,张海军,等.开关磁阻电机径向电磁力解析建模及有限元分析[J].煤炭学报,2012,37(4):700-704.
[9] 孙玉坤,吴建兵,项倩雯.基于有限元法的磁悬浮开关磁阻电机数学模型[J].中国电机工程学报,2007,27(12):33-40.
[10] 杨艳,邓智泉,曹鑫,等.无轴承开关磁阻电机径向电磁力模型[J].电机与控制学报,2009,13(3):377-382.
Torque Mathematic Model of 8/6 Switched Reluctance Motor with Two-Winding Excitation
LIBo,XIAOLin-jing,SUNChuan-yu,WENYi-cheng,XIAONan,CHENZhong-xia
(Shandong University of Science and Technology,Qingdao 266590,China)
In view of the torque of 8/6 switched reluctance motor (SRM) with two-winding excitation, the stator winding's self and mutual inductance were deduced based on the principle of 8/6 SRM and the method of magnetic equivalent circuit. Utilizing the method of magnetic field division, the gap permeance of 8/6 SRM was solved, and then the mathematic model of torque was derived. Finally, based on the results of finite-element analysis, the validity of the mathematic model was verified. The studies show that the mathematic model of torque can describe the output characteristics of 8/6 SRM correctly when the motor stays balanced.
switched reluctance motor; two-phase excitation; mathematic model; finite-element analysis
2016-01-13
山东省优秀中青年科学家科研奖励基金(BS2013NJ015);青岛市博士后研究人员应用研究项目(01020120521);青岛市应用基础研究计划项目(15-9-1-66-jch)
TM352
A
1004-7018(2016)08-0019-03
李波(1991-),男,硕士研究生,研究方向为磁悬浮技术。

