行波超声波电动机“跑道”形压电振子的模态分析

王笑竹，张 健

(营口理工学院，营口 115014)



行波超声波电动机“跑道”形压电振子的模态分析

王笑竹，张 健

(营口理工学院，营口 115014)

研究超声物料输送装置的压电振子，其工作模态为面内弯曲振动。通过动态设计找出两个频率相等波长相差45°的弯曲振型，实现跑道形振子面内弯曲行波，使上下横梁产生微观运动，通过物料与振子间的摩擦力完成物料输送。

超声波电动机;动态设计；行波；“跑道”形振子

0 引 言

超声物料输送装置是超声振动技术的实际应用。它利用超声振动技术进行物料的输送[1-2]。超声物料输送装置除具有超声波电动机的特点外，与传统输送装置相比，有以下优点[3]：无驱动装置，结构简单，易于加工制作；输送控制精度高；可控性好；无人体可感受的噪声和振动；不产生干扰电磁场，也不受电磁干扰信号的影响。在微量或少量物料输送领域有广阔的应用前景。

1 压电振子结构

本文设计的压电振子采用“跑道”形状，如图1所示，上下直梁段对称布置驱动齿(可以双面利用[4])。设计该压电振子的重点是寻找频率相等、波长相差45°的两个同阶弯曲振动模态[5]。

图1 振子结构

2 压电振子的数值分析及有限元分析

“跑道”形结构是由圆环演变而来的，根据等式r=(2πR0-2l)/2π[6](式中：R0代表圆环中心线半径，l表示“跑道”形结构直梁段长度，r表示“跑道”形结构的圆环半径),保持圆环轴线长度为一固定值，取R0=80 mm，“跑道”形梁的厚度h=4 mm，宽度b=6 mm，l/r=10，材料为黄铜，弹性模量E=110 GN/m2，密度ρ=8 400 kg/m3，分析当l与r成一定比例时，“跑道”形梁在相同阶次下两模态固有频率的变化规律。对B18阶模态的振型及固有频率进行分析，结果显示如图2所示。从图2中可以看出，同阶两个振型的固有频率一般不等，而且当保持l/r在一定数值范围内时，通过优化梁的几何结构尺寸，一般可以找到频率差几乎为零的振型，但当l/r继续增大时，将很难找到频率相近的两弯曲振型。

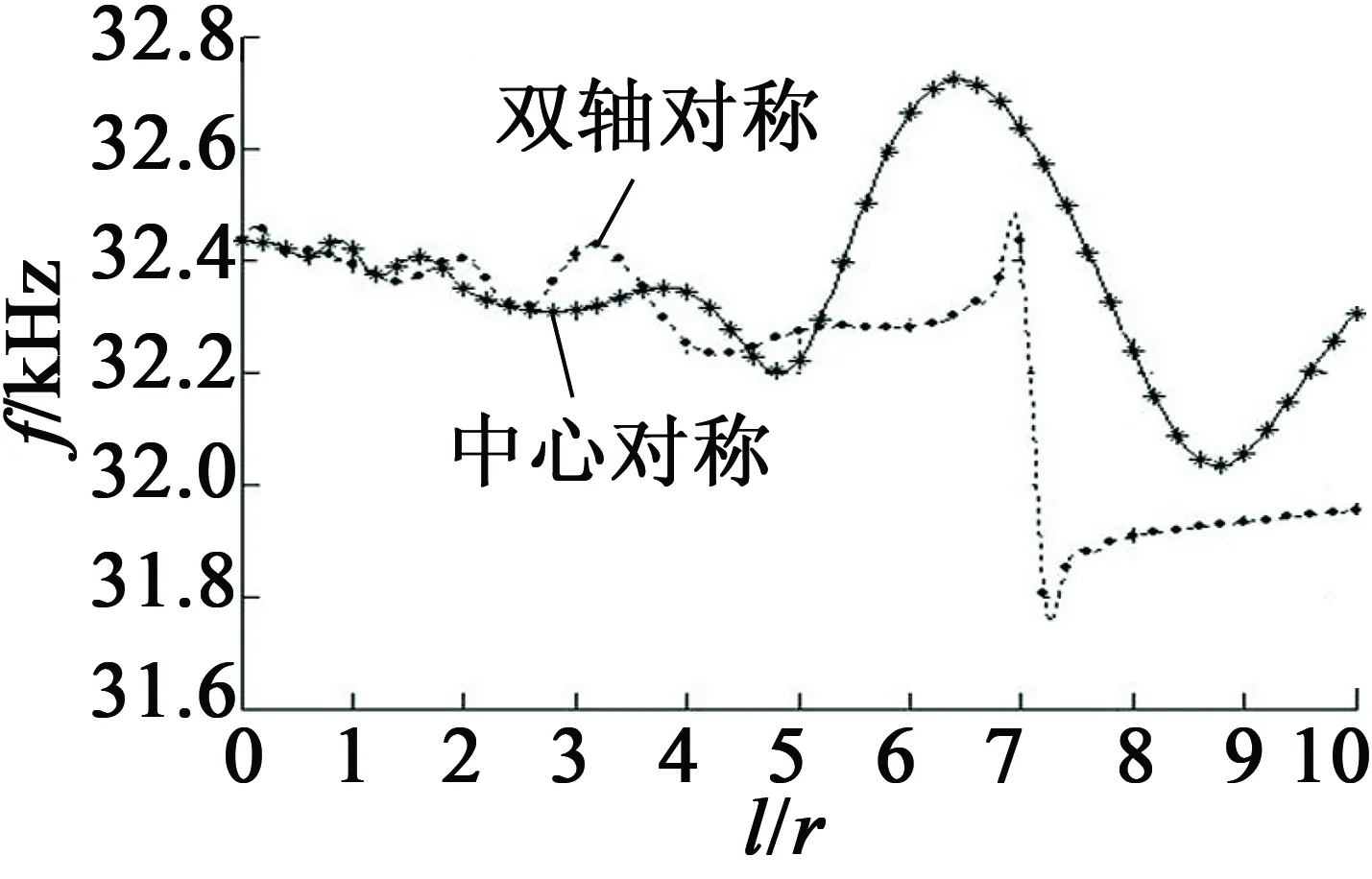
图2 B18阶两模态固有频率随l与r的变化

保持l与r的比值n不变，将l与r值同时扩大2倍，“跑道”形梁的厚度h也扩大2倍，宽度b保持不变，以R0=160 mm的圆环起始，仍然对B18阶模态的振型及固有频率进行分析，结果如图3所示。很明显，图3中的曲线与图2中对应的曲线形状基本一致，只是在相同n值下，同阶振型对应的两固有频率值几乎下降为原有尺寸下的1/2，由此推断，“跑道”形梁结构在保持几何学上相似的同时也保持了动力学上的相似。经过数值分析以及实际应用的需要，选18阶弯曲振型作为工作模态，该模态共振频率达到20 kHz以上，上下横梁长在210 mm附近。

图3 B18阶两模态固有频率随2l与2r的变化

运用ANSYS软件对振子的面内弯曲模态进行优化，最终获得输送振子的结构参数，如表1所示。有限元分析的两弯曲振动模态如图4所示，两固有频率分别为20 326 Hz和20 327 Hz，频率差为1 Hz。

表1 “跑道”形振子的结构参数

(a)f1=20326Hz(b)f2=20327Hz

图4 输送振子B18阶模态图

3 振子结构对模态的影响

振动模态与输送振子的设计密切相关，为了了解振子几何尺寸变化趋势对振动模态的影响，以下将就几何尺寸对振子B18阶模态的影响加以分析。对应图1，分析的主要对象：振子基体厚h1、齿高h2、凸台高h3、两端圆弧内半径r、齿缝隙l2以及压电陶瓷厚度ht。分析时，保证振子的其它尺寸不变，改变分析对象其一的尺寸，观察该尺寸对模态的影响，调整步长为0.1 mm，分析结果显示如图5所示。

(a)振子基体厚h1对固有频率的影响(b)振子齿高h2对固有频率的影响

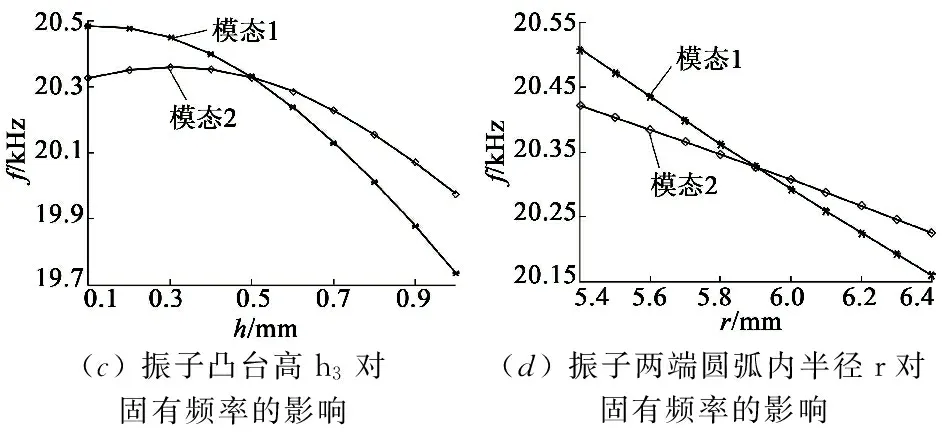
(c)振子凸台高h3对固有频率的影响(d)振子两端圆弧内半径r对固有频率的影响

(e)振子齿缝隙l2对固有频率的影响(f)压电陶瓷厚度ht对固有频率的影响

图5 振子尺寸对模态的影响

从图5中的各个图可以看出，在分析对象-振子基体厚h1、齿高h2、齿缝隙l2以及压电陶瓷厚度ht下的每两条曲线的重合度均比较好，说明这些参数的改变对两模态固有频率差值的影响不是很大，考虑加工精度时可适当放宽松些。但是从图5(c)、图5(d)看出，振子凸台高h3及两端圆弧内半径r这两个参数的变化对两模态固有频率差值的影响较大，故加工时要严格控制其尺寸精度。以上的分析结果不仅能够了解振子几何尺寸对模态影响的灵敏度，而且可以为今后该种类型输送振子的设计提供一定的理论依据。

4 实验研究

4.1 压电输送振子样机

输送振子的谐振频率最初是通过有限元进行数值分析得到的，与实际值往往有一定偏差，为了准确确定振子的工作频率，需对振子的谐振频率进行实验测定。

图6 实物照片

测试前需对振子的各部分进行标定：红、黄引线所在面为Ⅰ面，并定义为上直梁段，蓝、绿引线所在面为Ⅱ面，相应定义为下直梁段；与红、黄引线相焊接的陶瓷片记为Ⅰ组，相应与蓝、绿引线相焊接的陶瓷片记为Ⅱ组，具体标定如图7所示。

图7 振子引线分组示意图

4.2 模态测试及分析

激励电压设定为36V，分别激励Ⅰ组、Ⅱ组陶瓷片，测出B18阶两相工作频率分别为18 330Hz和18 420Hz，与模态分析的结果20 326Hz、20 327Hz

存在偏差，相差90 Hz，原因可能是建模时未考虑胶层对模态的影响，材料理论参数与实际参数的差异，以及振子在加工过程中产生的误差等。

如图8所示，实际的工作模态与有限元分析出的模态基本一致。由图9可见，B面也达到了良好的模态控制。

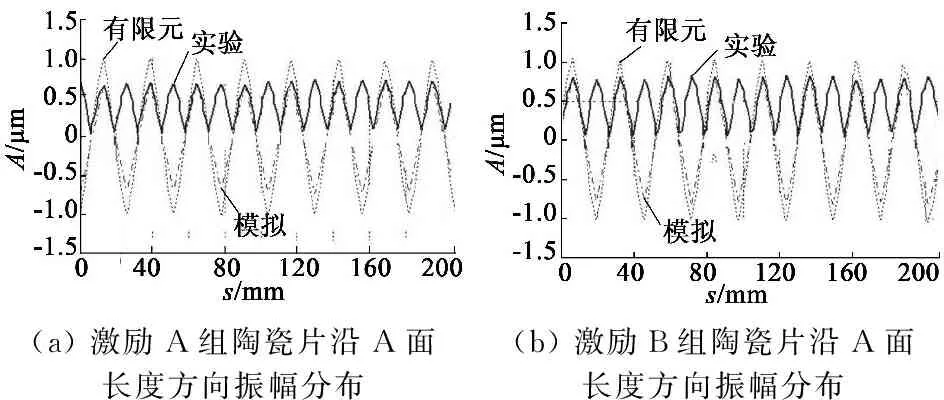
(a)激励A组陶瓷片沿A面长度方向振幅分布(b)激励B组陶瓷片沿A面长度方向振幅分布

图8 沿A面长度方向振幅分布

图9 沿B面长度方向振幅分布

5 结 语

利用有限元软件的模态分析找到了振子的两个B18阶面内弯曲振动模态，固有频率分别为20 326 Hz和20 327 Hz，频率差仅为1 Hz，满足工程要求。分析了振子主要几何尺寸对B18阶弯曲模态影响的灵敏度，分析表明振子的基体厚、齿高、齿缝隙以及压电陶瓷厚度的变化对两模态固有频率差值的影响不是很大，振子凸台高及两端圆弧内半径的改变对两模态固有频率差值的影响较大。

对振子进行了实验测试，测试出振子B18阶两相工作频率分别为18 330 Hz和18 420 Hz，频率相差90 Hz，对比理论分析的频率值有一定偏差，但A、B实际的工作模态与有限元分析出的模态基本一致，从行波合成角度出发，验证了理论分析中正交性的存在性。

[1] 李红双.驻波型超声物料输送装置理论与实验研究[D].锦州：辽宁工学院，2007.

[2] 张爱云.超声物料输送装置的驱动系统研究[D].锦州：辽宁工学院，2007.

[3] 何勍,李红双.压电振子弹性支撑的数值与实验研究[J].压电与声光,2007,29(5):619-621.

[4] 何勍,关亮,王宏祥.方环形直线驻波超声波电动机振子的动态设计[J].微特电机,2008,36(6):11-12.

[5] 王宏祥，何勍，关亮，等.方环形驻波直线超声电动机设计[J].微电机,2008,41(9):23-25.

[6] 何勍,王宏祥,于威.一种新型高频低幅振动给料装置的研究[J].机械科学与技术,2007,26(6):758-760.

Modal Analysis of a "Runway" Type Piezoelectric Vibrator of Traveling Wave Ultrasonic Motor

WANGXiao-zhu,ZHANGJian

(Yingkou Institute of Technology， Yingkou 115014，China)

The piezoelectric vibrator of ultrasonic feeding device was studied, which operation modes are in-plane bending, Two bending vibrations with same frequency and wavelength difference of 45° were found out by dynamic design to realize in-plane bending traveling wave of the vibrator. The micro elliptic motion was produced between up and down beams. The material transport was achieved through the friction between the material and the vibrator.

ultrasonic motor; dynamic design; traveling wave; “runway” vibrator

2015-04-20

营口理工学院院级科研项目(QNL201509，QNL-201514)

TM359.9

A

1004-7018(2016)04-0021-02