直线电动机伺服系统精确自动建模方法研究

柳 瑞，张 驰，沈林勇，赵 飞，董 良，李 荣

(1.上海大学，上海 200072；2.中国科学院 宁波工业技术研究院，宁波 315201)



直线电动机伺服系统精确自动建模方法研究

柳 瑞1,2，张 驰2，沈林勇1，赵 飞2，董 良1,2，李 荣2

(1.上海大学，上海 200072；2.中国科学院 宁波工业技术研究院，宁波 315201)

永磁同步直线电动机伺服系统具有复杂耦合性、部件参数测量难度大、不确定等特点，使理论与真实模型存在差异。频域特性直观反映系统的响应和运动性能，快速自动频域模型辨识具有重要意义。在dSPACE/MATLAB实验平台上产生正弦扫频信号，简便灵活。对比对数扫频实验与稳态步进逐点扫描实验曲线，结果表明对数扫频可以快速精确地获得频域特性。采用最小二乘综合零极点自动优化配置的方法拟合模型，实现快速准确建模。

永磁同步直线电动机；正弦扫频；频域特性；自动建模

0 引 言

目前，永磁同步直线电动机伺服系统在精密机床、电子制造等领域得到了广泛应用。伺服系统的控制性能决定着系统加工性能和效率[1]，为提高伺服系统控制性能就需要明确被控对象精确模型。磁场矢量控制实现电流稳态解耦，基于矢量控制建立永磁同步直线电动机模型是常用建模方法[2]，然而永磁同步直线电动机伺服系统具有复杂耦合性和各部件参数测量难度大、不精确等特点，基于理论模型与真实模型具有一定差异[3]。因此，通过系统响应辨识方法，获得实际系统模型具有现实意义，是进行控制器设计实现良好控制性能的基础[4-8]。

在工业应用领域中(如振动分析和伺服系统辨识)常采用频率辨识的方法，直接辨识系统的传递函数。实验室中常用正弦激励、随机激励和锤击法测量系统频响函数，正弦激励常用于航天航空模型的测试，具有相当可靠性[9]。

正弦扫频试验有正弦逐点扫描试验和瞬时频率变化扫频试验。前者是一种稳态正弦扫频，需满足系统在每一个频率点处都进入稳定状态，充分暴露系统特性，得到非常高精度的频响函数，但每次改变频率后需等待系统瞬态响应结束，比较耗时，并且较长时间的振动对系统容易造成损坏。

近几年随硬件发展，瞬时频率变化扫频试验得以发展，如Chirp信号扫频[10]和正弦扫频，缩短了扫频试验时间，并可以更加真实地模拟产品的工作环境[11]。Gloth[12]对逐点正弦激励、多点组合正弦激励、随机激励和扫频激励进行研究，使用慢扫频信号作为激励，既提供较大的推动力，又节省测试时间。文献[13]中通过设计正弦扫频的产生和综合分析，解决扫频信号的非稳态问题。针对直线电动机伺服系统非线性、小阻尼特性，合理选择扫频激励信号可提高系统辨识精度和节约测试时间[14]。

本文首先分析正弦扫频频域特性的测试原理，基于dSPACE/MATLAB半实物仿真实验平台实现扫频信号的生成和数据采样、处理，可替代价格昂贵的传统的频率特性测试仪和信号发生器，具有简便灵活、节约成本的优点。对于高速电机轻阻尼结构，研究扫频速率对系统的影响，用来选择最佳扫频速率；并进行正弦步进逐点扫频实验，对比验证正弦扫频测试系统频域特性的可靠性和快速性。采用最小二乘及零极点自动优化配置的模型拟合方法，实现快速准确建模。

1 正弦扫频激励频域特性测试原理

永磁同步直线电动机伺服驱动系统由运动控制器、驱动器、直线电动机、线性导轨、直线光栅、工作台等部件组成。基于dSPACE/MATLAB控制实验平台产生测试信号，编程方便，实时采集数据，可替代价格昂贵的传统的频率特性测试仪和信号发生器，便捷灵活，节约成本[15-17]。该系统模型辨识原理框图如图1所示，DS1103单板I/O模块DAC端口输出扫频激励信号，编码器端口连接电机位置光栅端口。ControlDesk实现实时测试界面，进行数据的采集和记录，将数据导入MATLAB中进行处理、分析和自动模型拟合，快速得到系统较精确数学模型。实际的辨识对象包括直线电动机、驱动器(电流环控制、滤波等)等，驱动器内部采用PI控制。

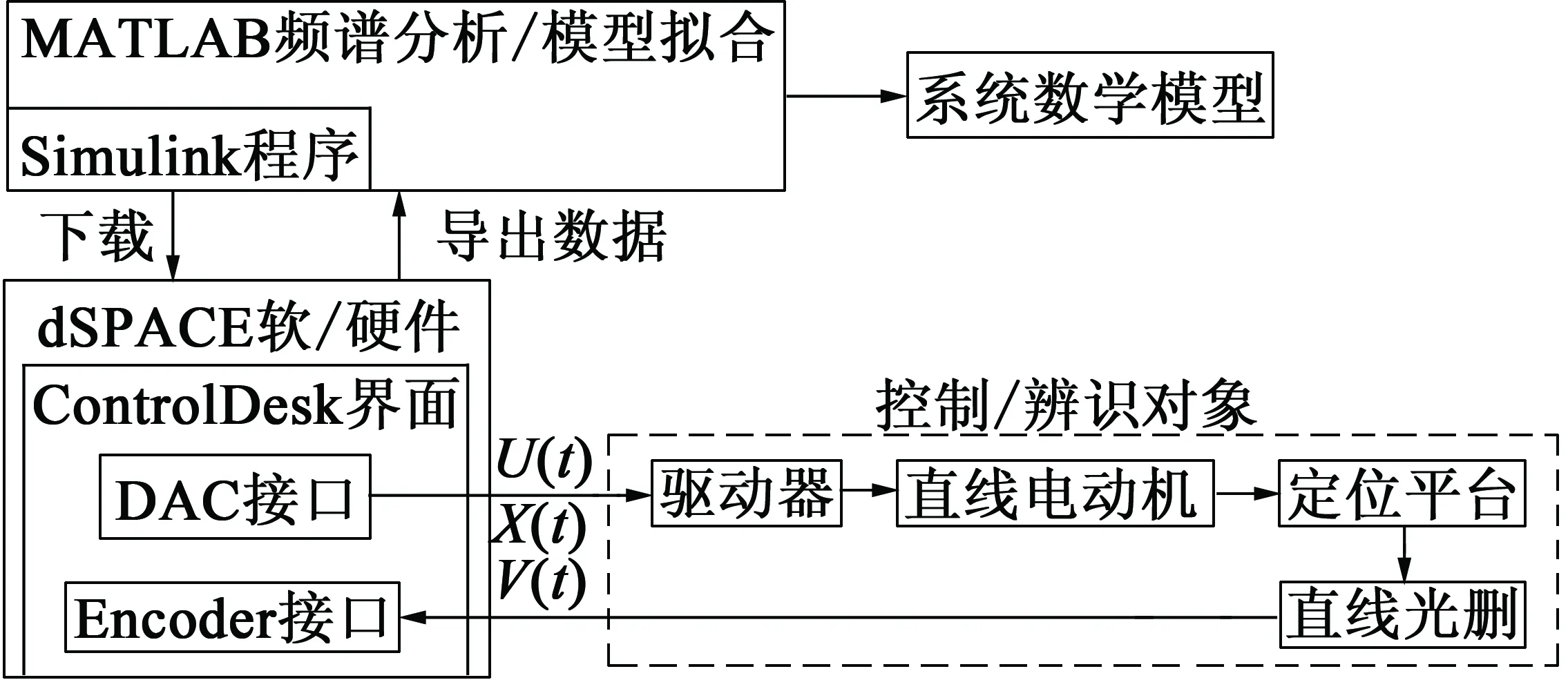
图1 永磁同步直线电动机系统模型辨识原理框图

1.1 正弦扫频信号

正弦扫频函数精确表达式：

(1)

式中：A(t)为幅值，一般为常数；φ0为初相位。根据频率的变化规律，可分为线性扫频和对数扫频。对比对数扫频与线性扫频频率变化特性，在低频时对数扫频频率变化较慢，频率间隔较小，更适合扫频实验。对数扫频频率表达式:

(2)

式中：f0为起始频率；r为扫频速率,表示每分钟r个倍频程(oct/min)。 c和φ0组成新相位值，对数扫频函数精确表达式：

(3)

基于以上推导，该信号在dSPACE/MATLAB控制实验平台上通过编辑Simulink程序实现。对数频率变化在扫频速率较低时，一个周期内频谱可认为单一谱线。针对实验选用的扫频速率，对数扫频信号25Hz处相邻两周期频率分别为25.368Hz和25.381Hz，前后周期频率相差甚小，可认为频率连续变化。

1.2 数据相关分析

实验采集得到的数据是时域数据，需将数据变换为频域数据。由于FFT分析整周期信号无泄漏，针对慢扫频信号频率连续变化，计算方便[18]。相关分析抑制噪声效果很好，步进逐点扫频用相关分析法可提高辨识精度[19]。

首先需要对时域测试数据进行预处理，数据预处理主要包括对高频噪声的滤波、粗大误差的剔除和稳态截取。由于速度信号是由位置值微分得到，慢扫频信号中主要存在差分时的高频噪声，对时域数据进行滑动平均滤波效果较好，计算简便。步进逐点扫频需得到系统稳态响应，当存在某些异常和响应非稳定时的数据需要剔除。对预处理后数据进行FFT谱分析和相关分析，FFT谱分析利用MATLAB计算简单方便；相关分析在实验平台实现原理如下。

设频率为f0的单位输入信号xi(t)，采集信号长度为N，采样间隔为Δt，待辨识系统响应：

(4)

式中：Af0为待识别信号幅值，φf0表示相位。分别计算yi(t)与单位信号sin(2πf0·iΔt)和cos(2πf0·iΔt)的相关函数：

(5)

由此得到正弦函数稳态响应的幅值和相位，即待辨识系统的幅相特性分别：

(6)

2 快速自动建模方法

由于该测试系统采用速度环开环系统，在低频段呈近似线性特性，利用最小二乘方法拟合模型，计算简便可靠。随着ω的增大，使得最小二乘拟合B(jω)增大，拟合误差增加[20]，故在中高频段通过获取频率曲线零极点并调整模态参数进行曲线拟合，即在频率特性曲线峰值处设置阻尼合适的极点，在波谷处设置相应零点，分别进行配置。对于更高频段，受各种不确定性影响较大，采用适当增益覆盖曲线，便可得到整个频段精确模型，同时含有未建模动态不确定性的模型，便于鲁棒控制设计，提高系统鲁棒性。

2.1自动查找系统零极点

由于在不同频段采用不同的建模方法，因此，需要合理划分低高频率段，并确定系统的零极点。在频率特性中含频率、增益和相位信息，通过对增益数据列的迭代比较找出曲线的转折点，即曲线极值点，同时也可能是系统零极点。考虑模态组合及测试误差，曲线不是严格意义上的单调光滑曲线，存在许多毛刺，增加了查找正确零极点的难度。

图2 确定曲线极大点原理框图

设置增益分辨率ΔMag已消除曲线毛刺的影响，其中以极大值点为例，自动查找程序原理如图2所示。为得到系统主要零极点，设频率分辨率ΔFreq范围内含有两个或多个相邻极大(或极小)点时，取极值最大(或最小)的一个作为系统零极点记录保存。该系统零极点如图 3所示，最终取频率最小的极点(或零点)的频率作为低频率段临界频率。

图3 自动查找系统零极点

2.2 低频段最小二乘拟合

最小二乘计算简便可靠，设系统传递函数：

(7)

在任意某个频率点处，极小化误差目标函数：

(8)

可得到拟合参数：

(9)

图4为对频率特性低频段拟合。可见低频段拟合精度较高。

图4 低频段模型

2.3 中高频段零极点配置自动建模

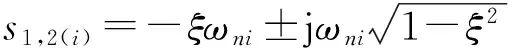
快速自动拟合曲线实现原理图如图5所示，通过自动求取合适的阻尼比ξ，使该频率段曲线的拟合误差小于很小的正常数，即确保拟合误差在一定范围内。

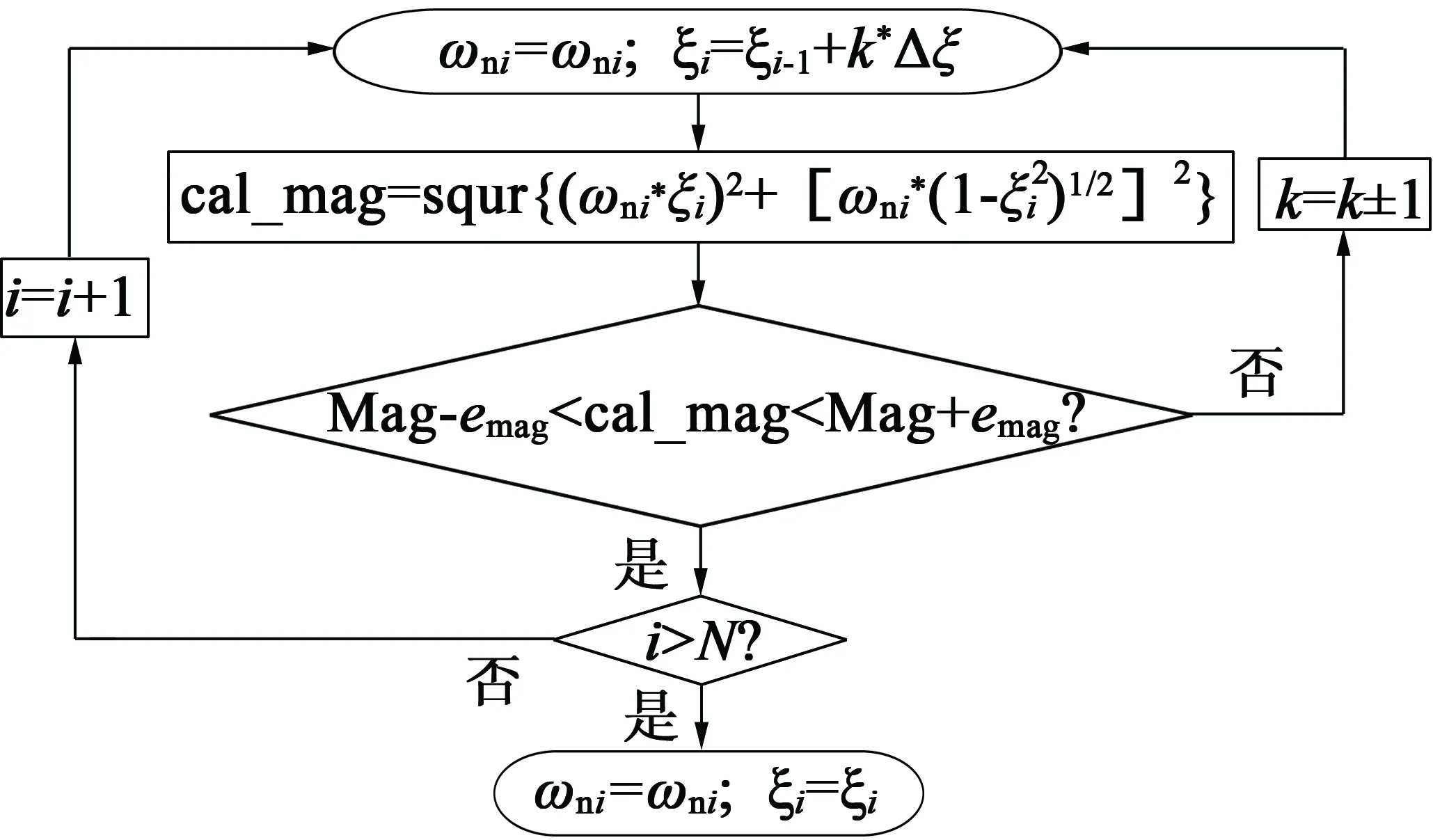
图5 配置零极点的自动拟合原理图

当ωn确定时，阻尼比ξ的大小决定着幅值增益，ξ越大幅值增益越小。依据此规律，以Δξ为其分辨率来改变ξ的大小，直到拟合误差满足要求。实验中各零极点频率值和阻尼比值如表1所示。频率值为图3中得到的各个零极点的频率，阻尼比为自动拟合值。

表1 系统调整后各点的阻尼比

3 实 验

实验选用辨识对象为自主研发的XY平台的X轴永磁同步直线电动机和CopleyXenus型驱动器，Copley驱动器设置为电流环差分模拟输入模式，设计电机参数和驱动器参数设置如表2所示，位置传感器为美国MicroE的MercuryⅡ型直线光栅尺。整体实验装置如图 6所示。

系统频率特性直观反映系统的响应速度、精度和运动平稳性。为直观显示系统理论模型与实际模型的差异，建立经典控制方法的理论模型。根据矢量控制的基本原理，对永磁同步直线电动机的电压方程、电磁推力方程和机械运动方程简化得到理论数学模型，仿真其频域特性如图7虚线所示。图7实线为实验得到系统频域特性，存在振动模态，经分析，中频段主要振动是有机械支撑结构引起；中高频段引起振动原因较为复杂。可见，理论模型不能反映实际驱动器部件特性和动子(或工作台)支撑结构的机械特性，故实际系统辨识很有必要，具有现实意义，是控制器设计的基础。

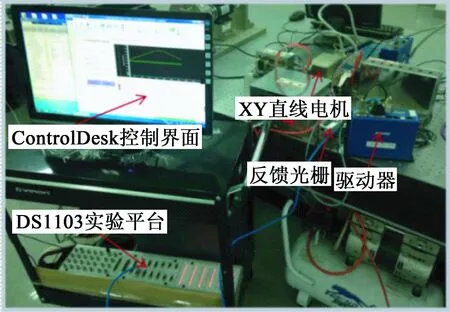
图6 基于ds1103的参数辨识实验台

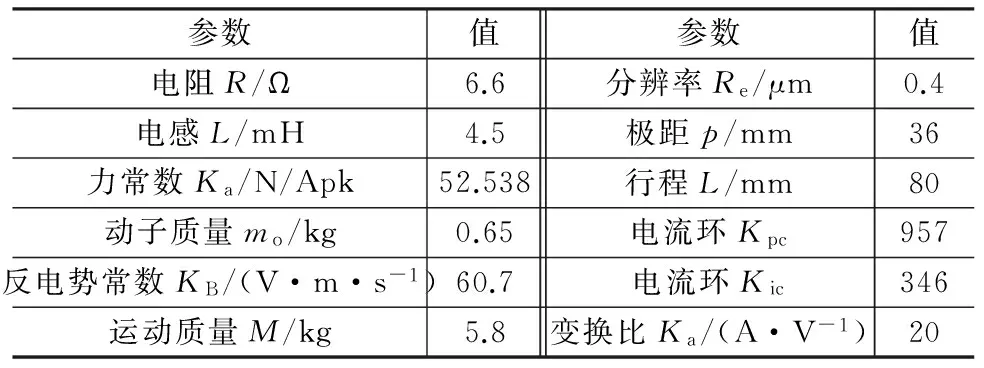
参数值参数值电阻R/Ω6.6分辨率Re/μm0.4电感L/mH4.5极距p/mm36力常数Ka/N/Apk52.538行程L/mm80动子质量mo/kg0.65电流环Kpc957反电势常数KB/(V·m·s-1)60.7电流环Kic346运动质量M/kg5.8变换比Ka/(A·V-1)20

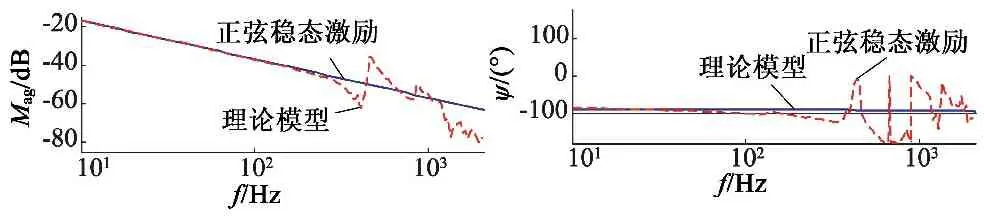
图7 系统理论模型和实际模型频域特性

在对数扫频试验中，扫频速率过大使得系统响应幅频特性峰值降低；速率过小时，由于速度信号是通过位置差分得到，使得测量噪声较大，会降低系统信噪比。选用不同的频率变化速率进行测试，综合评比峰值幅值和高频噪声影响，最终确定合适激励信号频率变化速率为1.32 oct/min，分别对实际系统进行正弦扫频和步进稳态扫频实验。系统实验结果如图 8所示，虚线是正弦稳态激励下的测试结果，由于系统响应在稳定条件下测得，可作为实际系统理想频率曲线；实线是对数扫频激励下测得的频域特性。对比实验结果，永磁同步直线电动机伺服系统正弦扫频激励方法具有相当可靠性和高效性。该伺服系统一阶共振频率在465 Hz附近。

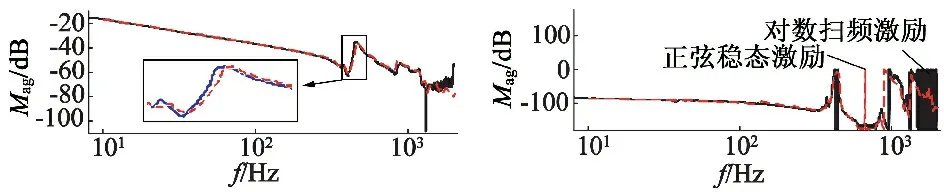
图8 实际系统扫频激励和步进稳态激励下频率特性

对扫频激励频率特性曲线使用最小二乘综合自动零极点配置进行拟合，拟合结果如图 9所示，低频段幅频特性尽量贴近实际曲线，绝对误差<0.5 dB，中高频段拟合模型的幅值频率特性曲线高于实际曲线，这样控制器设计时，就会加强对该频率振动的抑制，提高系统的鲁棒性；零极点处拟合绝对误差在3 dB左右，保证足够的幅值裕量的同时减小模型的相位损失。拟合模型与实际模型的误差符合建模要求。由于实际系统具有一定延时，为方便控制器设计，综合低频段与中高频段模型，得到8阶的系统模型传递函数表达式如式(9)，实现快速建模。

Gsys=(-13s7+1.202×105s6-4.077×108s5+

4.847×1012s4-2.542×1015s3+

4.542×1019s2-3.27×1021s+

1.227×1026)/(s8+1.122×104s7+

5.834×107s6+4.867×1011s5+

7.516×1014s4+5.104×1018s3+

2.764×1021s2+1.525×1025s+

该模型包含实际系统的未建模动态的不确定模型，为更好地实现系统的鲁棒控制提高鲁棒性提供了模型基础。

图9 频域特性系统模型拟合曲线

4 结 语

该辨识系统实验平台在dSPACE/MATLAB控制实验平台上实现，方便实现激励信号和响应数据的采样和处理，可替代传统的频率特性测试仪和信号发生器，便捷灵活，节约成本。推导对数扫频函数的精确描述，为准确快速获得实际伺服系统频率特性提供理论依据，减小较长时间的振动对系统的损坏。对实际系统最小二乘综合零极点自动优化配置拟合模型，快速实现准确建模，得到系统未建模不确定性模型，弥补理论模型的不足，并且自动保存零极点有利于控制器设计。

[1] 曹宇.伺服系统特性测试平台设计[D].武汉：华中科技大学,2013.

[2] 田艳丰.永磁直线同步电动机鲁棒控制策略研究[D].沈阳：沈阳工业大学,2010.

[3] 陈昊,王永,周建亮,凌杰.永磁同步电动机系统模型辨识[J].微特电机,2013,41(1):7-10.

[4] 张刚,刘品宽,张波,等.直线电机精密运动平台轨迹跟踪控制器设计[J].光学精密工程,2013,21(2):371-379.

[5] 陈正.基于非线性和柔性特性分析及补偿的直线电机精密运动控制[D].杭州：浙江大学,2012.

[6] CHEN Z,YAO B,WANG Q.Adaptive robust precision motion control of linear motors with high frequency flexible modes[C]//the IEEE 12th Int.Workshop Adv.Motion Control,Sarajevo,Bosnia and Herzegovina,2012.[7] CHEN Z,YAO B,WANG Q.Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect[J].IEEE/ASME Trans.Mechatron.,2013,18(3):1122-1129.

[8] CHEN Z,YAO B,WANG Q.Adaptive robust precision motion control of linear motors with integrated compensation of nonlinearities and bearing flexible modes[J].IEEE Trans.Ind.Informat.,2013,9(2):965-973.

[9] 谭志红.伺服控制系统的频域辨识及激励信号的研究[D].哈尔滨:哈尔滨工业大学,2010.

[10] 汪首坤,王军政.基于调频脉冲扫频的导弹舵机频率特性测试方法[J].北京理工大学学报,2006,26(8):697-699,703.

[11] 王帅,陈涛,李洪文,王建立. 光电跟踪伺服系统的频率特性测试与模型辨识[J]. 光学精密工程,2009,17(1):78-84.

[12] GLOTH G,SINAPIUS M.Analysis of swept-sine runs during modal identification[J].Mechanical Systems and Signal Processing,2004,18(6):1421-1441.

[13] 杨志东,丛大成,韩俊伟,等.正弦扫频振动控制中的信号综合与信号分析[J].振动工程学报,2008,21(3):309-313.

[14] GLOTH G,SINAPIUS M.Influence and characterization of weak non-linearities in swept-sine modal testing[J].Aerospace Science and Technology,2004,8(2):111-120.

[15] 张桅,赵剡,张寅.基于dSPACE的频率特性测试与模型辨识研究[J].宇航计测技术,2010,30(1):57-60.

[16] 郎宝华,杨建华,李榕.基于dSPACE的电机控制系统实验平台研究[J].现代电子技术，2010,33(17):130-132.

[17] 陈鹏展,唐小琦,李银刚.基于dSPACE的伺服控制模型实时仿真研究[J].微特电机，2008,36(9):25-27.

[18] 严侠,李晓琳,胡勇.运用正弦扫频实现电动振动台模型的频域辨识[J].装备环境工程,2015,(2):44-48.

[19] 陈连华,赵娜,王奕博,等.一种快速单步的频率特性测试方法[J].电子测量技术,2011,(2):77-79，101.

[20] ABDULLAH A，MAMUN T H,LEE T S.Low frequency domain identification of transfer function model of a disk drive actuator[J].Mechatronics,2002,12(4):563-574.

Linear Motor Servo System Precision Automatically Model Methed Research

LIURui1,2,ZHANGChi2,SHENLin-yong1,ZHAOFei2,DONGLiang1,2,LIRong2

(1.Shanghai University, Shanghai 200072, China;2.Ningbo Institute of Industrial Technology, CAS, Ningbo 315201, China)

Some characteristics of permanent magnet synchronous linear motor (PMSLM) like complex coupling, difficult measurement of parameter and uncertain parameters have resulted in the difference between the theoretical model and the actual one. Automatic and rapid model identification is of great significance as its frequency domain characteristics directly reflect the response and performance of the system. Different types of sine-sweep signals based on dSPACE/MATLAB platform were generated and tested. The frequency response curves generated by logarithmic sweep and stepped sweep were compared. The experimental results show that logarithmic sweep is a better option for acquiring frequency response quickly and accurately. Curve fitting with least squares method in low frequency range and automatic zero-pole optimized configuration in middle and high frequency range were implemented to fit the frequency response curve and tune the model. The results validate that the proposed modeling approach is a fast and accurate way.

PMSLM; sine frequency sweep; frequency domain characteristics; automatically model

2015-11-17

国家自然科学基金项目(51207158)；宁波市重大攻关项目(2013B10045)；国家科技支撑计划项目(2014BAF10B00)；中国科学院百人计划项目(Y30901W407)

TM359.4

A

1004-7018(2016)04-0009-04

柳瑞(1989-)，女，硕士研究生，研究方向为伺服驱动系统控制及振动抑制研究。