数学公式定理推导方法的“抉择”——以“余弦定理”为例

☉山东省高青县第一中学　王　晓　东李军

数学公式定理推导方法的“抉择”——以“余弦定理”为例

☉山东省高青县第一中学王晓东李军

众所周知，数学公式定理通常有多种推导方法，有的甚至多达十几种、数十种，乃至上百种.对于数学教学来说，并不是所有的方法都值得推崇.一方面，有些方法超出了学生的理解水平，即使讲了，学生未必能接受；另一方面，过度地追求推导方法不仅会耗费大量的课堂教学时间，而且容易偏离教学的主题.于是，我们不得不思考：如何选择合适的推导方法，既能使学生的数学思维得到充分的拓展，又能使课堂教学紧扣目标，自然生成.作为高中数学的经典定理——“余弦定理”，推导的方法至少有几十种.下面笔者就以“余弦定理”为例谈谈对此的看法.

一、关注前后联系，体现思维的连续性

数学是一门逻辑性很强、前后知识联系很紧密的学科，联系旧知识、学习新知识是学习数学的重要方法.乌申斯基有句名言：“智慧不是别的，而是组织得很好的知识体系.”数学知识的教学不是不加组织地向学生传授孤立的知识，教师要引导学生对知识间的联系加以组织和提炼.郑毓信教授也多次强调“数学教学不应求全，而要求联”.对于数学公式定理的推导来说，关注知识的前后联系，在已有的基础上学习新知，可以降低思维的难度，从而使推导过程自然流畅.

在余弦定理之前学生已经学习了正弦定理，经历了正弦的推导过程.那么在推导余弦定理时，能否沿袭正弦定理的证明思路推导余弦定理呢？正弦定理与余弦定理存在着天然的联系，它们不仅可以相互转换，而且推导方法也存在着相通之处.

教材（人教A版）中是通过在三角形中作高线构造直角三角形来推导正弦定理的，其实余弦定理也可以这样推导.

如图1，在锐角三角形ABC中，作CD⊥AB于D，则BC2=CD2+BD2=CD2+（AB-AD）2.而CD=bsinA，AD=bcosA，所以，a2=CD2+（AB-AD）2=b2sin2A+c2+b2cosA-2bccosA=b2+ c2-2bccosA，即a2=b2+c2-2bccosA.

图1

正弦定理还有一种常用的推导方法，那就是在构造三角形的外接圆，利用外接圆的几何性质已知把三角形转化为直角三角形来推导.余弦定理也可以采用类似的方法，只不过构造圆的方式有所差异.具体如下：

如图2，在△ABC中，以C为圆心，较短边CB为半径作圆，交AC及其延长线于F，E，交AB于G，作CD⊥AB于

因为AD-DB=c-2acosB，故b2=a2+c2-2accosB.

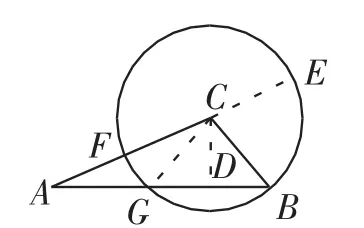
图2

图3

若以较长边CA为半径作圆，交BC的延长线于E，F，交BA的延长线于G，CD⊥AB于D，如图3所示.同理FB· BE=GB·AB⇒（AC-CB）·（BC+AC）=AB·（AD-DB），即b2-a2=c（AD-DB）.因为AD-DB=AB-2DB=c-2acosB，也可得到b2=a2+c2-2accosB.

以△ABC另外两个顶点为圆心，同样也可以得到余弦定理的另外两种形式.

教材（人教A版）余弦定理的推导采用的是构造向量法，方法虽然简单，但推导方法上的“另起炉灶”无形中隔断了两大定理的天然联系.

让学生把新知识转化为旧知识去认识和理解，实际就是促使学生调动已有的知识经验解决新问题，使新学习的材料与原有的知识建立联系，通过这个过程，学生对数学知识自然就融会贯通了.这样不仅有利于学生对知识形成规律性认识，而且有利于体现思维的连续性.

二、再现历史轨迹，锤炼思维的综合性

数学公式定理的起源、发展一般都有着丰富的历史背景.实践证明再现数学知识的历史演进过程不仅可以使学生获得了一种历史感，而且可以从新的角度审视数学，冲破思维的局限，对数学产生更敏锐的理解力和鉴赏力.

余弦定理是勾股定理的推广，其“雏形”最早出现在欧几里得的《几何原本》的第2卷中.勾股定理作为一个既古老又经典的数学定理，它的证明方法不下百种.既然余弦定理与勾股定理存在着密切的联系，那么它们之间的推导方法是不是也存在着共通之处.我们能不能从勾股定理的历史证明上找到推导余弦定理的线索.我们不妨回顾一下欧几里得是如何证明勾股定理的.

如图4所示，分别在直角△ABC的三边上作正方形ACDE、ABFG和BCHI，作CL⊥GF于L.连接BE和CG，则由AE和BC的平行关系，可得正方形ACDE的面积等于△AEB的两倍（同底等高）；由AG和CM的平行关系，可得长方形AMLG的面积等于△ACG的两倍.而△AEB≌△ACG，故知正方形ACDE和长方形AMLG的面积相等.同理，可得正方形BCHI与长方形BMLF的面积相等.于是就得到勾股定理：c2=a2+b2.

梳理勾股定理的证明思路，我们发现证明的关键是把代数式“c2=a2+b2”几何化，转化为正方形的面积.因此，余弦定理的证明也可以仿照勾股定理的证明，具体如下所示：

如图5所示，△ABC为锐角三角形，仿照欧几里得的做法，在其三边外侧分别作正方形ACDE、ABFG和BCHI；分别从三个顶点向对边作垂线，垂足分别为K、M和N，与正方形另一边的交点分别为L、P和Q.于是，SAMPE= SAKLG，SBNQI=SBKLF，因此，c2=SAMPE+SBNQI=a2+b2-（SMCDP+SNCHQ）.而又有SMCDP=b（acosC）=abcosC，SNCHQ=a（bcosC）=abcosC，故c2=a2+b2-2abcosC.

图4

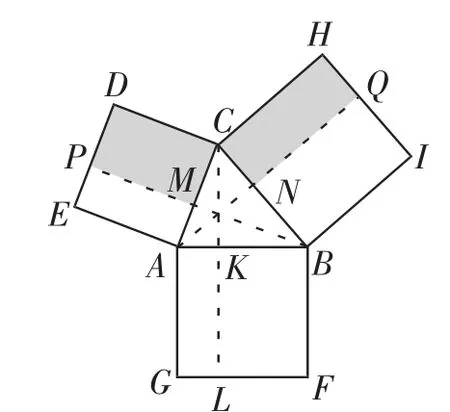
图5

图6

当△ABC为钝角三角形，构造如图6所示的图形，同理可以得到余弦定理.

以勾股定理为起点，用的几何方法来推导余弦定理，不仅可以弥补教材中证明方法的不足，而且可以使学生亲历数学发展的历史足迹，感悟数学思想方法的魅力，锤炼了思维的综合性.

三、把握知识整体，发展思维的创新性

系统论告诉我们，任何系统的整体功能等于各个部分功能之和加上各个部分相互联系而形成的结构功能.在部分功能不变的情况下，整体功能的大小取决于各个部分的联系.因此，在掌握部分知识之后，要把各个部分的知识联系起来，形成一个类别清楚、联系紧密的网络结构.对于数学公式定理而言，运用整体化思想来开展教学可以起到事半功倍的效果.

正弦定理、余弦定理本质上就是三角形边角关系的定量反应.从数学本质上看，它们原本就是一个整体.既然如此，能不能找到一种推导方法，同时得到这两个定理呢？

如图7，在△ABC中，三内角A、B、C所对的边分别是a、b、c，以A为原点，AC所在的直线为x轴建立直角坐标系，于是C点坐标是（b，0），由三角函数的定义得B点坐标是（ccos∠BAC，csin∠BAC），则b，csin∠BAC）.现将平移到，则∠DAC=π-∠BCA，所以=（acos（π-∠BCA），asin（π-∠BCA））=（-acos∠BCA，asin∠BCA）.因为，则有

图7

由②得acosC=b-ccosA，平方得a2cos2C=b2-2bccosA+ c2cos2A，即a2-a2sin2C=b2-2bccosA+c2-c2sin2A.而由①可得a2sin2C=c2sin2A，故a2=b2+c2-2bccosA.同理可证b2=a2+c2-2accosB，c2=a2+b2-2abcosC，这样也得到了余弦定理.

在同一证明过程中，同时得到两个定理，可谓“一箭双雕”.除了体现向量法在数学证明中的价值外，同时还进一步说明了正弦定理和余弦定理原本是“一对同胞兄弟”，它们本身就是一个整体.这样就可以把正弦定理与余弦定理合并成一节课，这对发展学生的创造性思维是有极大的作用.

综上，数学公式定理的推导与证明不在于方法的多少，而是能否找到条主线把这些“零碎”的方法串联起来，形成完整的体系，从而使学生在教师精心设计的问题探究中不断地发展数学思维能力.Z