基于EEMD奇异熵的高速道岔裂纹伤损检测

陈虹屹， 王小敏， 郭 进， 杨 扬

(西南交通大学信息科学与技术学院 成都，610031)



基于EEMD奇异熵的高速道岔裂纹伤损检测

陈虹屹， 王小敏， 郭 进， 杨 扬

(西南交通大学信息科学与技术学院 成都，610031)

针对高速道岔裂纹伤损特征提取及状态监测问题，提出一种基于集合经验模态分解(ensemble empirical mode decomposition，简称EEMD)奇异熵和最小二乘支持向量机(least square support vector machine，简称LSSVM)的高速道岔裂纹伤损检测方法。首先，通过EEMD方法将非平稳的道岔振动信号自适应地分解为有限个基本模态分量(intrinsic mode function，简称IMF)，每个IMF包含了原信号不同的特征尺度；然后,利用相关性分析筛选出与原始信号相关性最大的若干个IMF，计算所筛选IMF分量的奇异熵构成特征向量；最后,将多测点数据融合后的奇异熵特征向量输入LSSVM进行训练与测试，从而判断道岔的工作状态和伤损类型。模拟道岔裂纹伤损实验平台的振动信号分析及实验结果表明，在信噪比高于20 dB时，该方法受噪声影响小，算法稳定性好，能有效地用于道岔裂纹伤损检测。

裂纹检测； 高速道岔； 振动信号； 集合经验模态分解； 奇异熵； 最小二乘支持向量机

引 言

高速道岔是高速铁路线路中的重要组成部件，在轮轨相互作用及温度载荷等因素的作用下，道岔易发生折断、裂纹和剥落掉块等伤损形式，其中裂纹是导致道岔发生断裂、剥落掉块伤损的成因之一，具有危害大且检测困难的特点[1-3]。传统的以大型探伤车和小型探伤仪相结合的探伤机制虽然一定程度上可以检测出裂纹伤损，但存在检测效率低、占道检查影响行车效率等问题，难以满足我国高速铁路发展的需求。因此，研究道岔的裂纹伤损识别对保障列车高效、安全运行具有重要意义[3]。

振动信号为机械故障信息的载体，对其进行分析是故障诊断的常用手段[4]。对振动信号的处理包含2个重要过程：信号特征提取和故障状态识别，传统的信号特征提取方法以信号的平稳性为前提，无法对非平稳信号进行有效分析处理[5]。由于高速列车的轮轨相互作用是一个复杂的耦合动力学问题，所检测到的振动信号表现出非平稳特征，传统的信号特征提取方法具有一定的局限性。近年来，小波变换和经验模态分解(empirical mode decomposition， 简称EMD)[6]等非平稳信号分析方法在故障诊断领域得到了广泛应用。文献[7-8]将小波变换和奇异熵相结合应用于电力系统中，并结合支持向量机实现了对电力系统的故障诊断。但小波分析效果很大程度取决于小波基函数的选取，不具有自适应性。文献[9]利用EMD对轴承振动信号分解，根据奇异值差分谱理论对IMF分量进行消噪与重构，提取轴承故障频率。文献[10]针对钢轨振动信号，提出一种基于EMD和PSD(power spectral density,简称PSD)的钢轨伤损识别方法，并取得较好的效果。EMD克服了小波变换中小波基选择的困难，但存在模态混叠问题，影响信号局部特征的分析与提取。信号的间歇性是导致模态混叠的主要原因，而道岔属于铁路轨道中的活动部件，在列车的振动、重压和冲击作用下，其产生的振动信号包含有较多的冲击成分，利用EMD分解容易产生模态混叠，不利于道岔裂纹伤损特征的提取。

针对道岔裂纹伤损的自动检测问题，笔者提出一种基于EEMD奇异熵和LSSVM的道岔裂纹伤损检测方法。该方法采用EEMD分解出道岔振动信号的各个IMF分量，再将各分量的奇异熵经过多测点数据融合后作为特征向量，输入到LSSVM分类器判断道岔的工作状态及伤损类型。实验结果表明，EEMD奇异熵能够较好地反映道岔的裂纹伤损特征，多测点数据融合使不同传感器的信息相互补充，减小了伤损信息的不确定性，有效提高了裂纹伤损识别率。此外，在信噪比高于20 dB时，本方法受噪声影响小，算法稳定性好。

1 基于EEMD奇异熵的特征向量提取

EEMD是由Huang等[11-13]提出的一种噪声辅助数据分析方法。该方法通过在信号中添加均匀分布且幅值有限的高斯白噪声来减轻模态混叠，其本质是叠加白噪声的多次EMD分解[14]，适合于非线性、非平稳信号处理。同时，奇异熵具有奇异值分解挖掘数据基本模态特征的特性以及信息熵对信号复杂程度的度量功能，在机械信号信息量评估、信息成分分析等方面具有独特性能[15]。以奇异熵量化道岔振动信号，借助其包含的复杂度信息，可达到特征量提取的目的。将EEMD和奇异熵相结合来提取道岔的裂纹伤损特征，信号特征得到强化，伤损特征更加明显。

1.1 EEMD奇异熵计算过程

1) 向待分解的道岔振动信号x(k)中加入一个随机高斯白噪声序列n(k)，表示y(k)=x(k)+n(k)，其中y(k)为混有噪声后待分解的信号。

2) 对y(k)进行EMD分解得到q个IMF分量cj,m(j=1,2,…,q)，cj,m表示第m次试验分解出的第j个IMF。

3) 重复执行步骤1)和2)，共进行M次。利用不相关随机序列的统计均值为0的原理，将上述对应的IMF进行集总平均，消除多次加入白噪声对真实IMF的影响[16]，得到

(1)

4) 对IMF分量进行相空间重构。设第j个IMF分量cj={cj(k)}，将其元素cj(k)嵌入到(N-n+1)×n维相空间内，得到重构吸引子轨道矩阵

Xj=

(2)

其中：n为嵌入维数;N为信号采样点数[17]。

5) 对Xj进行奇异值分解，得到

(3)

其中：Λl×l为对角矩阵。

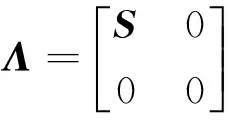
(4)

其中：S=diag (λj,1,λj,2,…,λj,l)，λj,b(b=1,2,…,l)为矩阵Xj的奇异值。

定义第j个IMF的奇异熵为

(5)

1.2 维数n对奇异熵的影响

由式(2)可知，奇异熵的计算结果与嵌入维数n有关。因此，本研究针对道岔振动信号对n的取值进行了分析。图1为维数n对道岔不同工况(正常、 裂纹深度1.5 cm、裂纹深度0.5 cm)下不同测点振动信号奇异熵的影响，可以看出，当时，3种工况的奇异熵不稳定，受n的影响较大；当时，奇异熵趋于稳定，且不同工况的奇异熵值区分度较大。考虑到n取值过大会增加矩阵分解的时间，因此在本研究中取n=400。

图1 维数n对奇异熵的影响Fig.1 The influence of dimension n on singular entropy

1.3 特征向量的提取步骤

1) 利用EEMD将信号x(k)分解为q个包含不同频率成分的IMF分量，根据式(2)求取每个分量的重构矩Xj(j=1,2,…,q)。

3) 根据式(5)计算第i个测点各IMF分量的奇异熵，构建特征向量

(6)

4) 针对单一传感器反映裂纹伤损信息的模糊性和不确定性，将不同测点的特征向量Hi依次首尾相连，得到最终的15维特征向量

(7)

2 基于LSSVM的裂纹伤损分类器

LSSVM是由Suykens等[18]提出的一种支持向量机(support vector machine，简称SVM)改进学习方法，该方法采用二次损失函数将SVM中的二次规划问题转化为求解线性方程组，在保证精度的同时大大降低了计算复杂性，加快了求解速度[19]。

LSSVM 是一种两类分类器，针对多分类问题，需要采用多类支持向量机处理方法。本研究利用性能较好的一对一方法[20]构建道岔裂纹伤损识别模型。该方法是在每两类之间建立一个分类器，对于r类问题，需要构建r(r-1)/2个分类器，文中对道岔的3种工况进行识别，因此需3个支持向量机分类器，其网络结构如图2所示。其中：输入E11,E12,…,E35为奇异熵特征向量；输出y为道岔的3种工况。

图2 道岔裂纹伤损识别网络结构图Fig.2 Structure of turnout flaw detection network

3 实验仿真及结果分析

3.1 实验数据采集

由于实际列车过岔时不易采集到有裂纹伤损的道岔振动信号，因此本实验所用数据来源于图3(a)所示的9号道岔裂纹伤损实验平台。该平台模拟了正常、裂纹深度0.5 cm和裂纹深度1.5 cm 3种道岔工况类型，裂纹伤损模拟如图3(b)所示。实验采用力锤激励方式拾取道岔振动信号，力锤的型号为L1301B，灵敏度为0.097 mV/g，量程为50 g。传感器为LT0102的压电加速度传感器，安装位置如图4所示。其中：测点1位于道岔尖端；测点2位于道岔中部；测点3位于道岔尾端。实验数据采样频率为51.2 kHz，分析数据长度为1 280点。

图3 高速道岔裂纹伤损模拟实验平台Fig.3 High-speed rail flaw simulation platform

图4 传感器安装示意图Fig.4 The installation diagram of the transducer

3.2 道岔裂纹伤损特征向量提取

图5为不同工况下道岔测点1的振动信号时域波形，采用EEMD方法将各原始信号分解为频率由高到低的IMF分量，其中白噪声标准差取0.2，集合次数M取100。

图5 道岔3种工况的振动信号Fig.5 Turnout vibration signals of three conditions

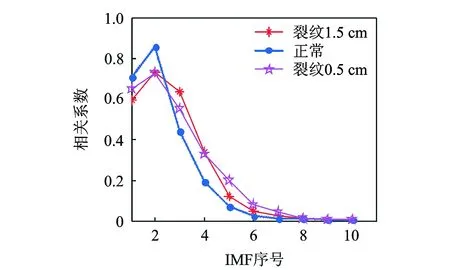
图6 IMF分量与原始信号的相关系数Fig.6 The correlation coefficient of IMFs with the original signals

图7 测点1处不同工况下奇异熵分布Fig.7 The singular entropy distribution under different working conditions of position 1

图8 裂纹0.5 cm不同测点的奇异熵分布Fig.8 Singular entropy distribution of different positions crack of 0.5 cm

图9 EEMD奇异熵的3维空间分布图Fig.9 Three-dimensional space distribution of EEMD singular entropy

因为EEMD方法是一种主成分分析方法[16]，主要的裂纹伤损信息集中在前几个IMF分量中。为了找出能够反映原始信号特征的有效分量，计算各IMF分量与原始信号的相关系数，如图6所示。由图可知，前5个IMF分量与原信号的相关性较大，包含原信号的主要信息，而其他高阶IMF与原始信号的相关系数均在0.1以下，可视之为噪声分量和虚假分量。因此，选取前5个IMF分量作为奇异熵的数据源。对每个测点3种状态信号进行EEMD分解并计算前5个IMF分量的奇异熵，形成特征向量矩阵，部分奇异熵分布如图7,8所示。从图中可以看出，正常和裂纹伤损两种工况在同一测点其奇异熵分布不同，不同裂纹损伤程度的奇异熵分布相似，但大小存在差异。另外，道岔不同位置由于振动传导路径及对裂纹伤损的敏感程度不同， 同一工况在不同测点其奇异熵分布也不相同。因此，笔者在EEMD特征提取的基础上采用多传感器数据融合处理，按照式(7)将不同测点的奇异熵组合，得到道岔各工作状态下的特征向量。图9为道岔不同工况下奇异熵E15，E25和E35的3维空间分布图，可以看出，正常和裂纹伤损两种工况表现出了较好的的聚类特征，但不同裂纹损伤程度的数据间存在交叉混叠现象，不易区分。因此，为了更准确可靠地识别道岔不同工作状态，可将奇异熵特征向量输入LSSVM进行分类识别。

3.3 实验结果分析

为验证方法的有效性，分别采集道岔不同工况下每个测点的振动信号(正常工况60组，裂纹0.5 cm和裂纹1.5 cm各56组)，共172组样本数据，随机选取其中112组(正常工况40组，裂纹0.5 cm和裂纹1.5 cm各36组)用于样本训练，其余用于测试。考虑到实验选取样本的随机性，本研究取20次实验结果的平均值作为最终测试结果。

3.3.1 算法比较

分别计算单个测点和3个测点融合后的裂纹伤损识别结果，得到测点1为72.20%，测点2为68.75%，测点3为76.26%，本方法为88.19%。可以看出，基于多测点振动信号的综合分析，具有充分利用多传感器信息冗余性和互补性的优点，单个测点的特征向量经过3点融合处理后，测试样本的裂纹伤损识别率达到88.19%。为了进一步验证笔者 方法的有效性，数据实验还采用了其他4种方法进行对比，每种方法均取不同测点融合后的奇异熵作为特征向量，结果如表1所示。可以看出，基于EEMD奇异熵和LSSVM的裂纹伤损检测方法充分利用了EEMD分析非平稳信号的优势和LSSVM处理小样本问题的良好性能，分类效果优于其他4种方法，且实时性强，为快速实现道岔故障诊断提供了一条新途径。

3.3.2 噪声的影响

由于实测道岔振动信号在采集过程中不可避免会受到不同程度的污染，因此，本研究在原始振动信号的基础上分别添加不同信噪比的高斯白噪声、高斯色噪声及冲击噪声，并对其进行仿真分析。其中高斯色噪声由方差为1的高斯白噪声通过一个4阶带通滤波器产生[21]。冲击噪声由公式n′(k)=B(k)G(k)产生，其中：G(k)为均值为0，方差为1的高斯白噪声；B(k)为伯努利过程。

图10为不同信噪比下本方法的测试结果，可以看出，在信噪比高于20 dB时，该方法受3种噪声影 响小，稳定性好；当信噪比低于20 dB时，识别率逐渐下降。主要是因为较低信噪比下噪声会淹没道岔工作状态的特征信息，从而影响裂纹伤损类型的准确辨识。因此在对实测振动信号分析过程中，为获取更好的裂纹伤损识别效果，有必要对信号进行去噪处理来突出其特征。

图10 不同信噪比的测试结果Fig.10 The test results of different signal-to-noise ratio

表1 不同伤损识别方法的测试结果

4 结束语

笔者提出了一种基于EEMD奇异熵和LSSVM的高速道岔裂纹伤损检测方法，该方法首先对道岔不同测点振动信号进行EEMD分解，获得若干个包含有主要裂纹伤损信息的IMF，然后将各IMF奇异熵经过多测点数据融合后作为裂纹伤损特征向量，输入到最小二乘支持向量机中进行分类，可以有效识别出道岔的工作状态。信号经EEMD 分解后其伤损特征更加明显，受噪声干扰小。多测点数据融合又使不同测点的伤损信息相互补充，减小了单一测点伤损特征信息的模糊性和不确定性，从而提高了裂纹伤损的识别率。通过对模拟伤损实验平台的振动信号分析及对比实验，验证了本方法的有效性，为道岔进一步故障诊断提供了一定的参考价值。

[1] 陈丹丹, 王小敏, 王平, 等. 基于顺序统计滤波的高速道岔振动信号端点检测[J]. 铁道学报, 2013, 35(11): 60-65.

Chen Dandan, Wang Xiaomin, Wang Ping, et al. High-speed turnout vibration signal endpoint detection based on order statistic filtering[J]. Journal of the China Railway Society, 2013, 35(11): 60-65. (in Chinese)

[2] 谢云叶, 周素霞, 谢基龙, 等. 表面裂纹连续扩展规律的仿真试验研究[J]. 工程力学, 2009, 26(5): 31-36.

Xie Yunye, Zhou Suxia, Xie Jilong, et al. Simulation and experiment research on continual extension rule of 3d surface crack[J]. Engineering Mechanics, 2009, 26(5): 31-36. (in Chinese)

[3] 王平. 高速铁路道岔监测技术研究报告[R]. 成都：西南交通大学, 2013.

[4] 张淑清, 孙国秀, 李亮, 等. 基于LMD近似熵和FCM聚类的机械故障诊断研究[J]. 仪器仪表学报, 2013, 34(3): 714-720.

Zhang Shuqing, Sun Guoxiu, Li Liang, et al. Study on mechanical fault diagnosis method based on LMD approximate entropy and fuzzy C-means clustering[J]. Chinese Journal of Scientific Instrument, 2013, 34(3): 714-720. (in Chinese)

[5] 许小刚, 王松岭, 刘锦廉. 基于小波包能量分析及改进支持向量机的风机机械故障诊断[J]. 动力工程学报, 2013, 33(8): 606-612.

Xu Xiaogang, Wang Songling, Liu Jinlian. Mechanical fault diagnosis of fan based on wavelet packet energy analysis and improved support vector machine[J]. Journal of Chinese Society of Power Engineering, 2013, 33(8): 606-612.(in Chinese)

[6] Huang Norden E, Shen Zhang, Long Steven R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society, 1998, 454(1971): 903-995.

[7] 朱艳伟, 石新春, 李鹏. 多分辨率奇异谱熵和支持向量机在孤岛与扰动识别中的应用[J]. 中国电机工程学报, 2011, 31(7): 64-70.

Zhu Yanwei, Shi Xinchun, Li Peng. Classification of islanding and grid disturbance based on multi-resolution singular spectrum entropy and SVM[J]. Proceedings of the Chinese for Electrical Engineering, 2011, 31(7):64-70. (in Chinese)

[8] He Zhengyou, Fu Ling, Lin Sheng, et al. Fault detection and classification in EHV transmission line based on wavelet singular entropy [J]. IEEE Transtractions on Power Delivery, 2010, 25(4): 2156-2163.

[9] 张超, 陈建军, 徐亚兰. 基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J]. 振动工程学报, 2011, 24(5): 539-545.

Zhang Chao, Chen Jianjun, Xu Yalan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J]. Jounal of Vibration Engineering, 2011, 24(5): 539-545. (in Chinese)

[10]Zhang Xin, Wang Yan, Feng Naizhang, et al. Flaw detection in high speed train′s rail based on EMD and PSD [C]∥Instrumentation and Measurement Technology Conference (I2MTC). Hangzhou: IEEE, 2011: 1-5.

[11]Wu Zhaohua, Huang Norden E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[12]Jiang Fan, Zhu Zhencai, Li Wei, et al.Fault identification of rotor bearing system based on ensemble empirical mode decomposition and self-zero space projection analysis[J]. Journal of Sound and Vibration, 2014, 333(14): 3321-3331.

[13]Lei Yaguo, He Zhengjia, Zi Yanyang. Application of the EEMD method to rotor fault diagnosis of rotating machinery [J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1327-1338.

[14]陈仁祥, 汤宝平, 吕中亮. 基于相关系数的EEMD转子振动信号降噪方法[J]. 振动、测试与诊断, 2012, 32(4): 542-546.

Chen Renxiang, Tang Baoping, Lü Zhongliang. Enesemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 542-546. (in Chinese)

[15]杨文献, 任兴民, 姜节胜. 基于奇异熵的信号降噪技术研究[J]. 西北工业大学学报, 2001, 19(3) : 368-371.

Yang Wenxian, Ren Xingmin, Jiang Jiesheng. On improving the effectiveness of the new noise reduction technique based on singularity spectrum[J]. Journal of Northwestern Polytechnical University, 2001, 19(3): 368-371. (in Chinese)

[16]张超, 陈建军, 杨立东, 等. 奇异值熵和支持向量机的齿轮故障诊断[J]. 振动、测试与诊断, 2011, 31(5): 600-604.

Zhang Chao, Chen Jianjun, Yang Lidong, et al. Fault diagnosis of gear based on EEMD entropy of singular values and support vector machine[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 600-604. (in Chinese)

[17]王林鸿, 吴波, 杜润生, 等. 用奇异谱和奇异熵研究数控工作台动态特征[J]. 振动、测试与诊断, 2012, 32(1): 116-119.

Wang Linhong, Wu Bo, Du Runsheng, et al. Dynamic characteristic of numerical control table with singular spectrum and singular entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(1): 116-119. (in Chinese)

[18]Suykens J A K, Vandewalle J. Least squares support vector machine classifies[J]. Neural Processing Letters, 1999, 9(3):293-300.

[19]万书亭, 佟海侠, 董炳辉. 基于最小二乘支持向量机的滚动轴承故障诊断[J]. 振动、测试与诊断, 2010, 30(2): 149-152.

Wan Shuting, Tong Haixia, Dong Binghui. Bearing fault diagnosis using wavelet packet transform and least square support vector machines[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2): 149-152. (in Chinese)

[20]Hsu C W, Lin C J. A comparison of methods for multiclass support vector machines [J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425.

[21]李月, 杨宝俊, 石要武. 色噪声背景下微弱正弦信号的混沌检测[J]. 物理学报, 2003, 52(3): 2-5.

Li Yue, Yang Baojun, Shi Yaowu. Chaos-based weak sinusoidal signal detection approach under colored noise background[J]. Acta Physica Sinica, 2003, 52(3): 2-5.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.05.005

*中国铁路总公司科技研究开发计划资助项目(2014X008-A，2013X012-A-1,2013X012-A-2)；国家自然科学基金资助项目(61371098)；四川省应用基础研究资助项目(2015JY0182)

2014-07-31；

2014-11-24

TH17； TN911.7

陈虹屹,男,1989年8月生,硕士生。主要研究方向为道岔振动信号处理。

E-mail:18280245736@163.com

简介：王小敏,男,1974年4月生，博士、教授、博士生导师。主要研究方向为轨道交通大数据与信息安全。

E-mail:xmwang@swjtu.edu.cn