弹性边界条件下圆板横向自由振动特性分析

石先杰, 李春丽, 蒋华兵, 康 甜

(中国工程物理研究院总体工程研究所 绵阳, 621900)



弹性边界条件下圆板横向自由振动特性分析

石先杰, 李春丽, 蒋华兵, 康 甜

(中国工程物理研究院总体工程研究所 绵阳, 621900)

采用谱几何法(spectro-geometric method, 简称SGM)分析了弹性边界条件下圆板横向自由振动特性。首先,将圆板的振动位移容许函数描述为一种谱形式的改进三角级数，并采用沿边界均匀分布的约束弹簧来模拟弹性边界条件；然后，将未知级数展开系数看作广义变量，应用瑞利-里兹法从能量的角度推导弹性边界条件下圆板结构横向自由振动系统特征矩阵方程;最后，设计搭建了相关实验台架，对圆板结构横向自由振动模态参数进行测试。将文中方法计算结果与文献解、有限元计算结果和实验结果进行对比，验证了谱几何法求解圆板横向自由振动问题的正确性和计算精度。

圆板； 横向自由振动； 谱几何法； 弹性边界条件

引 言

圆板作为结构基础部件，广泛应用于航空航天、船舶工程、石化容器及铁路交通等工程领域。板结构在外界激励载荷作用下产生的剧烈振动常常会造成结构的疲劳破坏、机械故障、能量损耗，并降低结构的可靠性等性能。此外,结构还将通过振动向周围环境辐射噪声。因而，圆板结构的振动特性受到相关专家学者的广泛关注。

几十年来，学者们围绕圆板结构振动问题做了大量的研究。有限元法[1]，能量法[2]和微分求积法等[3]各种解析或数值分析方法被相继提出并用于求解圆板结构的动力学问题。Leissa[4]对板结构振动研究成果进行了较为全面系统的总结。Wu等[5]采用广义微分求积法对径向变厚度圆板自由振动问题开展了相关研究。Chen等[6]采用基于径向基函数的无网格法求解了固支圆板和矩形板的自由振动问题。Yalcin等[7]采用微分变换法(differential transformation method，简称DTM)分析了简支、固支和自由边界条件下圆板的自由振动特性。Bauer等[8]研究了混合边界条件(固支、简支和自由边界条件的任意组合)下圆板的固有振动频率。

从上述研究情况来看，现有的研究方法大多限于特定的经典边界条件，且为了适用于各种不同的边界条件，大多需要不断修改位移容许函数、相关的算法及相应的求解过程。而在实际工程应用中，圆板结构往往具有更加复杂的边界条件，不仅包括固支、简支和自由这三种经典边界条件的任意组合，还包含弹性边界约束条件[9]。此外，还存在局部约束的情况。

针对上述技术局限性和实际的工程需求，采用谱几何法[10-11]建立弹性边界条件下圆板结构横向自由振动分析模型。通过将文中方法求解结果与相应文献解和有限元法结果进行对比，验证文中方法的正确性和有效性。随后，搭建相关实验台架，开展圆板横向自由振动实验测量研究。

1 理论推导

1.1 圆板模型描述

为了克服圆板圆心处易出现的奇异现象，拟建立如图1所示的环板模型，通过将内外半径比设置为极小的数(b/a=10-5)来模拟圆板[12]。在板结构r=a的边界上布置两类连续的边界约束弹簧，分别为线性位移弹簧(kt)和旋转约束弹簧(Kr)。通过改变约束弹簧的刚度值大小来模拟不同边界条件。当约束弹簧刚度值均设置为无穷大或零时，分别模拟固支和自由边界条件。当线性位移弹簧刚度为无穷大，而旋转约束弹簧刚度为零时，则为简支边界条件。

1.2 振动位移容许函数的级数表述

为了构建满足弹性边界条件的振动位移容许函数，并确保位移容许函数及其任意场点处空间坐标微分的连续性，采用谱几何法将圆板结构的振动位移容许函数描述[13-14]为

(1)

其中

(2)

其中:Amn和Bmn分别为位移函数的未知级数展开系数。

此处，在标准傅里叶余弦级数基础上，径向(s)上引入四项正弦函数的目的在于消除振动位移容许函数及其相应空间导数在结构边界上潜在的不连续性(或跳跃)现象，并去除Gibbs效应，以提高改进三角级数在整个求解域(包含边界)内的收敛速度与求解精度。

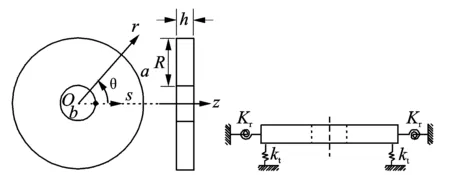
图1 弹性边界圆板横向振动模型Fig.1 Transverse vibration model of circular plate with elastic boundary condition

为了阐明这点，假设一个函数f(x)在[0, π]区间上Cn-1连续，并且第n阶导数绝对可积(第n阶导数可能在某些点不存在)。三角级数的部分和表示为

(3)

从数学意义上可以证明级数展开系数满足

(4)

如果系数am(m<0)可以表达为

(5)

更明确地预测收敛速度，式(5)可以描述为

(6)

这意味着

(7)

由此可以看出,收敛性在没有额外代价的基础上大幅提高了。值得指出的是，级数式(3)的收敛性可以通过设置合适的P值来控制。然而，对于一个给定边值问题的解的光滑性在数学上是由在控制微分方程中出现的最高次微分来决定的。以文中研究的圆板横向振动问题为例，其控制微分方程要求三阶导数连续且四阶导数在整个求解区域存在。因此，需要设定P=2来求取C3的强解，或者设定P=1来获得弱解。由于当前级数的光滑性在整个求解区域是可控的，则未知级数展开系数可以通过强解形式或弱解形式来求解。

由于构建的位移场函数在整个求解域是足够光滑的，则弱解和强解在数学意义上是等效的。文中将级数展开系数看作广义坐标，并采用瑞利-里兹法来求解,这样的解决方案更适合后续组合结构的振动建模。

1.3 求解方案

弹性圆板结构横向自由振动的系统拉格朗日函数为

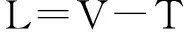
(8)

其中：V和T分别为结构系统的总势能和总动能。

总势能V包含板结构应变能和边界约束弹簧储存的弹性势能两部分，可以描述为

(9)

其中：D=Eh3/(12(1-μ2))为弯曲刚度；E为材料弹性模量；μ为泊松比；θ0和θ1分别代表边界约束弧长的起始角度(0≤θ0≤θ1≤2π，通过调整θ0和θ1可以方便地求解任意局部边界支撑下圆板振动问题)。

圆板结构横向振动引起的总动能T为

(10)

其中：ρ为材料密度；ω为圆频率。

将式(1)代入式(8)，采用瑞利-里兹法对位移场函数中的各个未知系数Amn和Bmn分别取极值，在实际计算过程中，改进三角级数进行有限截断m=M，n=N，从而可以获得关于未知级数展开系数的系统方程

(11)

其中：K和M分别为圆板结构的刚度矩阵和质量矩阵，其元素仅仅与板结构的材料特性、几何参数和边界条件相关，并直接决定了板结构系统的固有振动特性，即固有频率及其对应的模态振型；X为一个包含所有未知级数展开系数的向量。

显然，板结构的固有频率及其特征向量可以通过式(11)而获得。在求解框架中，通过将所得到的相应特征向量系数代入至振动位移场函数式(1)，即可获得该阶模态频率所对应的物理模态振型。如需对某种外界载荷作用下的结构响应进行求解，仅需在系统的拉格朗日函数中增加外界载荷的做功项即可，最终在结构系统方程，式(11)右侧出现外力激励向量。一旦板结构的位移确定后，其他感兴趣变量(如功率流、导纳等)可以通过对位移函数直接进行相关数学操作而得到。

2 数值算例与实验结果分析

2.1 数值算例分析

采用第1节的理论模型，对不同边界条件下圆板结构的自由振动特性进行计算分析，将文中方法的计算结果与文献解和有限元法结果进行比较，验证文中方法和编写程序的有效性与可靠性。在仿真模型中，圆板结构材料特性为：E=2.1×1011Pa，μ=0.3，ρ=7 850 kg/m3。由文中的物理模型描述可知，弹性边界条件可以通过改变边界约束弹簧刚度值而简单获得。对固支边界条件，可以将所有约束弹簧刚度值设置为无穷大(在数值计算中，取为1013)即可，而振动位移场容许函数的级数截断均取为M=N=12。

自由边界条件代表了模型验证的一种经典，但极具挑战性的边界条件。表1给出了自由边界条件下圆板前6阶最小无量纲频率参数(Ω=ωa2(ρh/D)1/2。作为参考数据，文献[15]和[16]的计算结果也列在表1中。从表中的数据对比分析可知，文中方法计算结果与文献[15]和[16]方法求解结果吻合良好。

表1 自由边界条件圆板前6阶最小频率参数Ω

Tab.1 The lowest six natural frequency parametersΩfor circular plate with free boundary condition

模态阶次文中方法文献[15]文献[16]15.3565.3575.35828.9989.0029.003312.43512.43312.439420.47520.46620.475521.81321.82021.835633.49133.46333.495

表2列出了不同旋转约束刚度Kr下简支圆板前6阶最小无量纲频率参数Ω。Kr=0和1013时，边界条件分别为简支和固支。通过表2的对比分析可知，文中方法计算结果与文献结果吻合程度较高。图2绘制了Kr=105时圆板前4阶模态振型情况。

表2 不同旋转约束刚度Kr下简支圆板前6阶最小频率参数Ω

Tab.2 The lowest six natural frequency parametersΩfor simply supported circular plate with variousKr

Kr模态阶次12345604.93213.89625.61229.70939.95648.478(4.935)(13.898)(25.613)(29.719)(39.957)(48.479)104.93613.89825.61329.72139.95848.4791035.01113.96325.67429.77940.01748.5371057.98517.35829.33533.56043.86452.531101110.21621.25934.87339.75951.02960.827101310.21621.25934.87339.75951.02960.827(10.216)(21.260)(34.877)(39.771)(51.031)(60.829)()括号内的结果引自文献[16]。

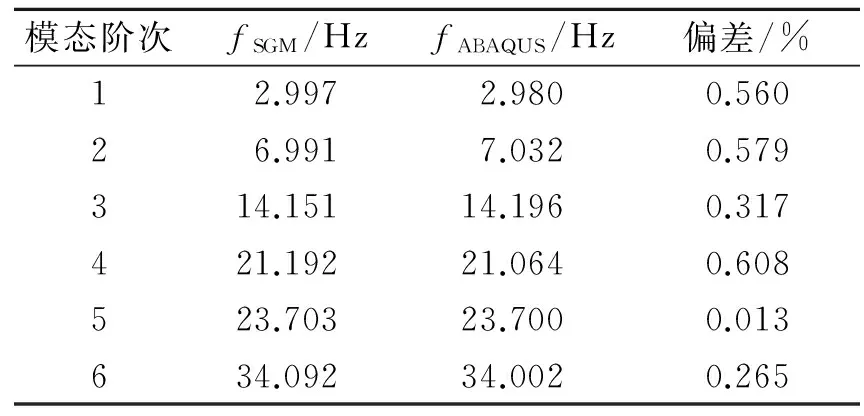
由第1节理论模型分析可知，文中构建的分析模型不仅可以适用于匀质边界条件和弹性边界，还可用于局部约束情况。因此，最后给出一个局部弹性边界约束条件的算例，在r=a边界存在局部匀质弹性约束，约束区间为(π/3, π)，而弹簧刚度值为Kr=kt=106。表3给出了局部弹性约束下圆板结构前6阶固有频率，ABAQUS的计算结果也列在表3中作为参考数据。

从表3的对比分析可以发现，两组计算结果之间吻合程度良好，最大相对偏差仅为0.608%，满足相关工程实际应用的需求。图3为圆板结构前4阶模态振型图，同时也列出了ABAQUS分析获得的模态振型图，从而验证了文中方法对局部弹性约束结构振型求解的准确性。

图2 Kr=105时简支圆板前4阶模态振型Fig.2 The first fourth mode shapes for simply supported circular plate with Kr=105

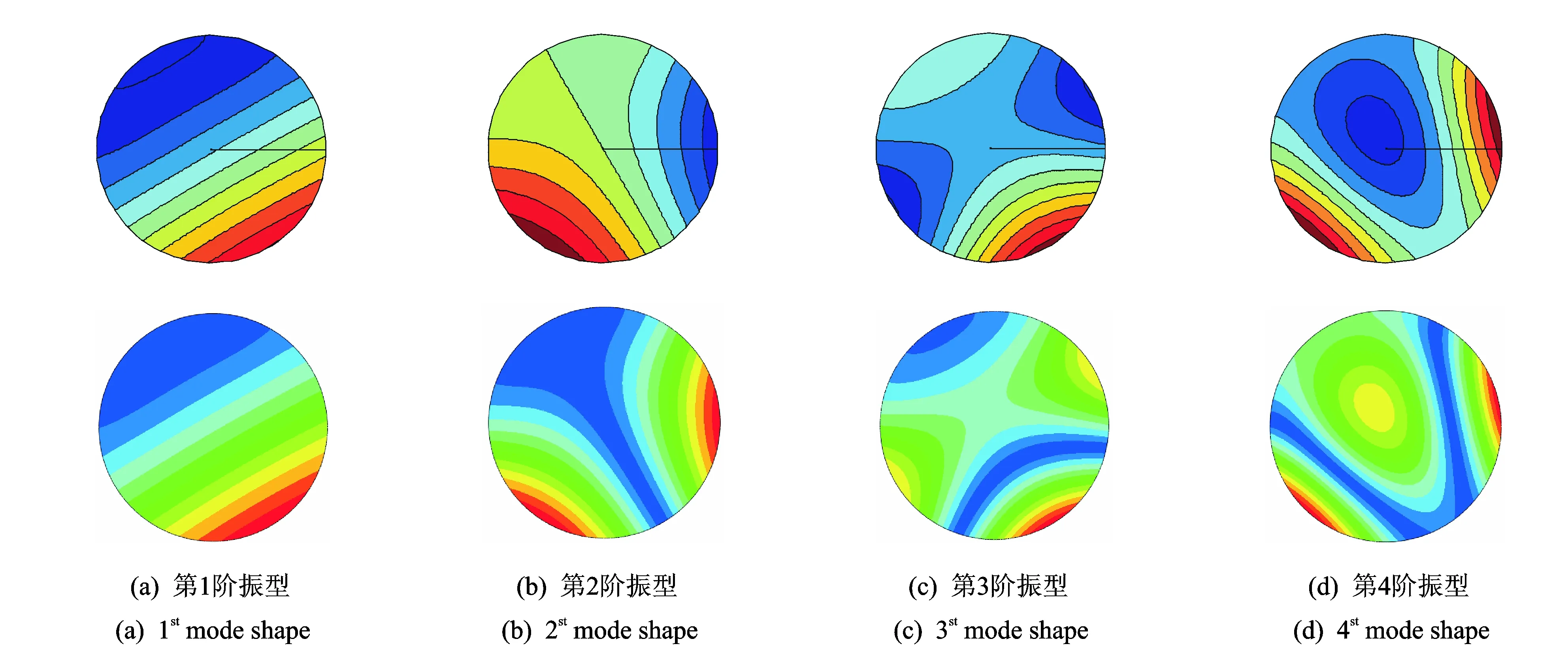
图3 (π/3, π)弧弹性约束(Kr=kt=106)圆板前4阶模态振型(第1行为文中方法结果，第2行为ABAQUS分析结果)Fig.3 The first fourth mode shapes of circular plate (with the arc (π/3,π) elastic restraint, Kr=kt=106): the first row is calculated by present method; the second row is calculated by ABAQUS

表3 (π/3, π)弧弹性支撑圆板前6阶固有频率(Kr=kt=106)

Tab.3 The first six natural frequencies for circular plate with the arc (π/3, π) elastic restraintKr=kt=106

模态阶次fSGM/HzfABAQUS/Hz偏差/%12.9972.9800.56026.9917.0320.579314.15114.1960.317421.19221.0640.608523.70323.7000.013634.09234.0020.265

2.2 圆板横向自由振动实验

图4 圆板振动实验装置Fig.4 Vibration experiment setup of circular plate

为了从实验角度对圆板横向振动进行研究，搭建如图4所示的实验台架。将半径为126.95 mm、厚度为5.68 mm的圆板，通过边缘位置的两个细小吊孔，采用橡皮绳连接后吊挂于支架上来实现横向振动的自由边界条件。在实验过程中，采用力锤在圆板表面沿垂直于圆板平面方向进行敲击，以激起圆板横向振动的弯曲波分量。圆板表面径向和周向分别划分为4和16等份，加上圆心处的1个测点，共计65个测点。依次在每一位置点处采用压电式加速度传感器DH131拾取力锤敲击所激起的弯曲振动响应信号，力锤和加速度计的输出信号则用多通道数据采集分析仪DH5922来采集，最后通过模态分析计算，获得圆板结构的模态参数。模态测试结果如表4所示。模态振型分布测量与仿真结果部分对比情况如图5所示。

表4 自由圆板前6固有频率预测与实验结果对比

Tab.4 Comparisons of the first six natural frequencies of circular plate with free boundary conditions between the predicted and test results

模态阶次fSGM/Hzfexperiment/Hz偏差/%1481.97482.340.082809.69793.132.0931119.181072.124.3741841.921809.031.8251964.151992.291.41

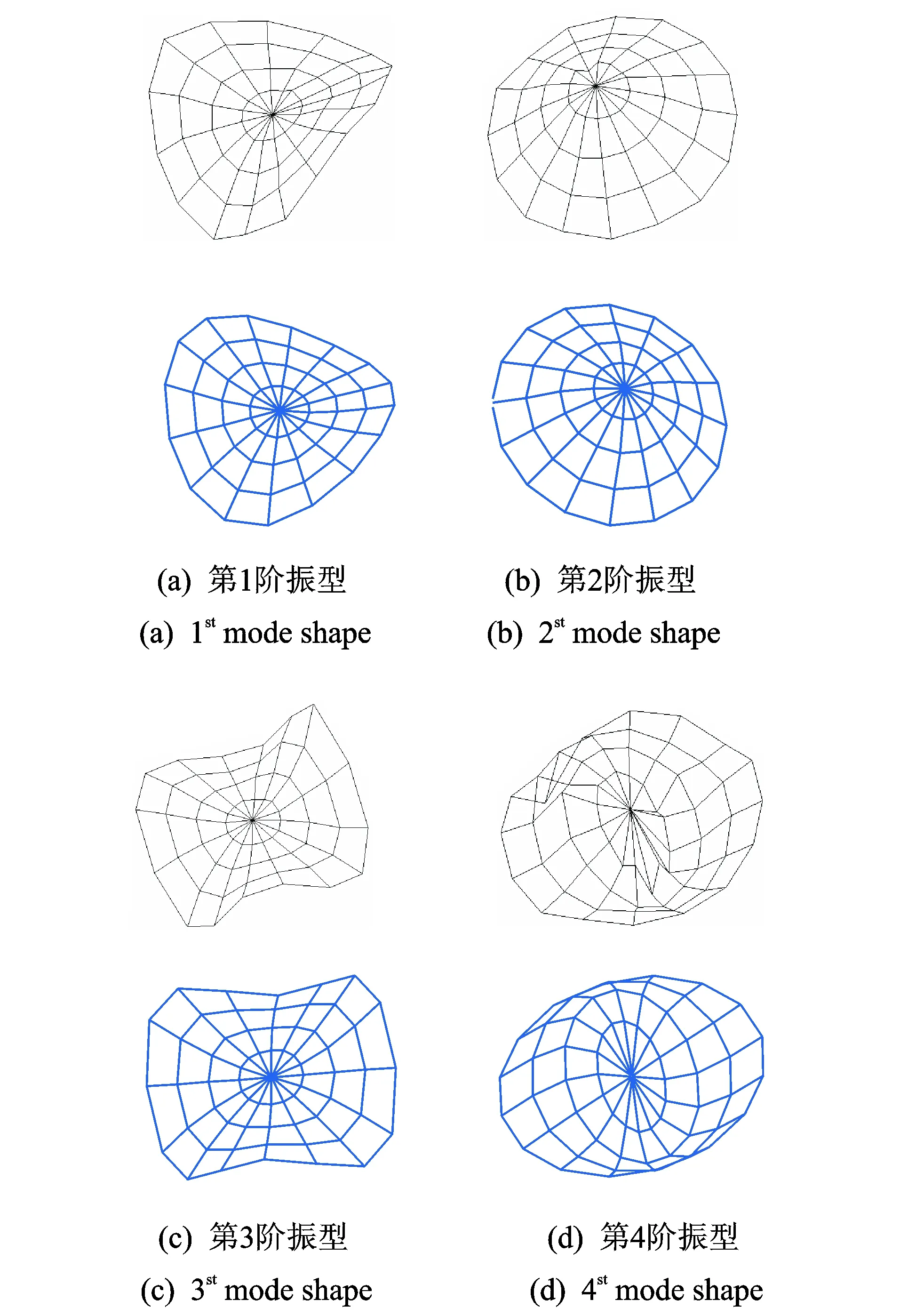
图5 圆板横向振动模态振型实验与预测结果对比(第1行为测试结果，第2行为预测结果)Fig.5 Comparisons of vibration mode shapes of the circular plate between measured and predicted results (The first row is the measured results, the second row is obtained by the present method)

从表4的对比情况可知，两种结果的吻合程度良好，再次验证了文中构建的分析模型的正确性。从振型对比图可以看出，除了个别测点的振动幅值过大或过小外，两种振型的形状和变化趋势基本保持一致。由于在模态实验过程中敲击的轻重、偏离节点位置和敲击过程中导致加速度传感器的微幅移动均会使获得的测量数据与实际振动情况之间存在着一定的数据偏差，且实验结果没有数值仿真结果那样光滑均匀。

3 结 论

1) 弹性边界支撑条件下圆板结构横向自由振动位移场容许函数可表示为一种通用的改进三角级数形式。

2) 对级数进行相应截断后，随着级数截断项数的增加，计算结果快速收敛，并且具有良好的数值稳定性。

3) 当改变边界条件时，文中方法不需重新推导及编程，只需改变边界约束弹簧刚度即可快速求解圆板横向自由振动特性。

[1] Liu C F, Lee Y T. Finite element analysis of three-dimensional vibrations of thick circular and annular plates[J]. Journal of Sound and Vibration, 2000, 233(1): 63-80.

[2] Rajalingham C, Bhat R B. Axisymmetric vibration of circular plates and its analog in elliptical plates using characteristic orthogonal polynomials[J]. Journal of Sound and Vibration, 1993, 161(1): 109-118.

[3] Gupta U S, Lal R, Sharma S. Vibration analysis of non-homogeneous circular plate of nonlinear thickness vibration by differential quadrature method[J]. Journal of Sound and Vibration, 2006, 298(4): 892-906.

[4] Leissa A W. Vibration of plates[M]. Washington DC: US Government Printing Office, 1969: 1-32.

[5] Wu T Y, Liu G R. Free vibration analysis of circular plates with variable thickness by the generalized differential quadrature rule[J]. International Journal of Solids and Structures, 2001, 38(44): 7967-7980.

[6] Chen J T, Chen I L, Chen K H, et al. A meshless method for free vibration analysis of circular and rec-

tangular clamped plates using radial basis function[J]. Engineering Analysis with Boundary Elements, 2004, 28(5): 535-545.

[7] Yalcin H S, Arikoglu A, Ozkol I. Free vibration analysis of circular plates by differential transformation method[J]. Applied Mathematics and Computation, 2009, 212(2): 377-386.

[8] Bauer H F, Eidel W. Determination of the lower natural frequencies of circular plates with mixed boundary conditions[J]. Journal of Sound and Vibration, 2006, 292(3): 742-764.

[9] 史冬岩，孔令成，石先杰，等.弹性边界板结构拓扑优化声辐射[J].振动、测试与诊断，2014，34(1)：179-184，197.

Shi Dongyan, Kong Lingcheng, Shi Xianjie, et al. Topology optimization and sound radiation research of plates with elastic boundary[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 179-184，197. (in Chinese)

[10]Li W L. Free vibrations of beams with general boundary conditions[J]. Journal of Sound and Vibration, 2000, 237(4): 709-725.

[11]Li W L, Zhang Xuefeng, Du Jingtao, et al. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J]. Journal of Sound and Vibration, 2009, 321(1-2): 254-259.

[12]Mirtalaie S H, Hajabasi M A. Free vibration analysis of functionally graded thin annular sector plates using the differential quadrature method[J]. Proceedings of

the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2011, 225(3): 568-583.

[13]Shi Dongyan, Shi Xianjie, Li W L, et al. Free transverse vibrations of orthotropic thin rectangular plates with arbitrary elastic edge supports[J]. Journal of Vibroengineering, 2014, 16(1): 389-398.

[14]Shi Xianjie, Shi Dongyan, Li Wen L, et al. A unified method for free vibration analysis of circular, annular and sector plates with arbitrary boundary conditions[J]. Journal of Vibration and Control, 2016, 22(2): 442-456.

[15]Liu K M, Yang B. Three-dimensional elasticity solutions for free vibrations of circular plates: a polynomials-Ritz analysis[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 175(1-2): 189-201.

[16]Zhou Zhenhuan, Wong K W, Xu Xinsheng, et al. Natural vibration of circular and annular thin plates by Hamiltonian approach[J]. Journal of Sound and Vibration, 2011, 330(5): 1005-1017.

10.16450/j.cnki.issn.1004-6801.2016.05.026

国家自然科学基金资助项目(51505445);中国工程物理研究院重点学科资助项目(计算固体力学)

2015-08-10；

2015-10-30

TH113; TB53

石先杰，男，1985年7月生，博士、工程师。主要研究方向为结构振动与噪声控制等。曾发表《任意边界条件下环扇形板面内振动特性分析》(《振动工程学报》2014年第27卷第1期)等论文。

E-mail: 411shixj@caep.cn