数学情境教学中启“知”策略探讨
李 三 平,郭 梦 敏
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
数学情境教学中启“知”策略探讨
李 三 平,郭 梦 敏
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
在以“以境启知,以知怡情”为主要特点的数学情境教学中,数学“知”识的形成过程是连接“境”与“情”的关键环节。而有效地启“知”(即从情境化的问题到问题的知识化过程)策略主要为以下三个方面:启“知”前,创设情境立足教学任务;启“知”中,去情境化时渗透数学化思想;启“知”后,再情境化时注重数学应用。
知;数学情境教学;去情境化;数学化
一、引言
由于数学内容、方法与呈现形式的高度抽象性,以及中小学学生认知发展遵循从具体到抽象、直观到严谨等规律,更由于情境教学不仅较好地将现实生活情境与抽象知识的学习联系起来了,而且还顺从了学生的认知发展规律,因而情境教学在中小学课堂中得到了一线教师的广泛认可和使用。
与此同时,21世纪初期的新一轮基础教育课程改革突出强调了数学教学要“从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成为数学模型并进行解释与应用的过程,进而使学生对数学理解的同时,在思维能力、情感态度与价值观等多方面得到进步与发展”,[1]这更进一步使情境教学在中小学数学课堂教学中得到了重视。由于对抽象知识的教授与讲解历来是大多数教师的强项,从而在数学情境教学中对情境创设的若干问题在近十几年的课堂教学研究中的比重逐年上升。然而一项关于中小学学生解决数学真实性问题的调查表明,虽然当下的课堂教学重视数学情境的创设,但是学生应用数学的意识与能力却未发生人们期望中的变化。[2]究其原因,可能主要在于部分教师在情境教学中扭曲了情境创设对具体问题“数学化”活动的催化作用,忽视了在具体情境中引导学生发现问题、探究问题并数学化地解决问题的“去情境化”这一理论抽象环节。
数学情境教学的主要特点是“以境启知,以知怡情”,[3]设“境”主要为了启 “知”,通“知” 才能逐渐怡 “情”,而启“知”的过程则是一个从情境的问题化到问题的知识化过程。因此在从“境”到“情”的情境教学中,“知”的形成过程是连接“境”与“情”的关键环节。
那么在数学情境教学中,如何更好地启“知”呢?本文试着从“去情境化”与“数学化”整合的角度,进行初步的探讨。
二、概念辨析
1. “去情境化”
人们较早的“去情境化”的观念是传统教学对教学所持的基本看法,认为知识一旦从具体情境中抽象出来,便成为具有与情境相一致的概括性知识;由于这些概括性的知识反映了具体情境的“本质”,因而对它们的学习便可以独立于现场情境进行,并且学习的结果可以自然地迁移到各种真实情境中。[4]显然,这种以概念表征为教学中心[5]的教学观点,不仅割裂了抽象学科知识与具体生活情境之间的联系,也忽视了具体情境的灵活变化性以及学生的认知发展规律,从而导致大多学习者尽管在学校收获了较多的理论知识,但其中的多数却是较难运用到现实生活中的“惰性”知识。
对于这种去情境化的教学弊端,教育家杜威辩证地指出了具体情境与抽象知识间的关系,即:概念、技能和信念需要在一种情境中才能体现出它们的意义并显得有用。同样,情境需要靠概念、技能和信念去将经验变得被理解,并促进知识的建构[6],并主张学生从真实的活动中通过意义建构获得知识,即“做中学”。在知识迅猛增长的当代信息化社会,尽管“做中学”“似乎”较为低效,“好像”难以使学生在较短时间内掌握大量的人类知识的精华,但其所倡导的在课堂教学中创设生活情境的做法是值得肯定的。因此,情境教学论者强调学习要在“真实”情境中进行,当然,这里的真实情境并不一定是真正的物理情境,但应该能够使学生在其中经历与真实世界相类似的认知挑战。
那么,如果单靠课堂上的情境化设置与学生的意义建构,缺乏教师深邃数学知识的指导,则容易走向情境教学的绝对化。这也就是为什么数学情境的设置虽然能够激发学生上课的积极性、调动学生已有的知识与经验,但仍会出现无法提高学生运用课堂所学数学知识解决各种问题的能力的情形。这时候,我们就必须清楚地看到数学情境教学必定包括“去情境化”的过程,此时的“去情境化”指的是帮助学生超越特定情境以实现必要的数学抽象[7],这实际上也是学校数学教学所要完成的重要任务——培养学生严谨、抽象等的数学思维。而数学抽象是一个去生活、去情境的过程,是把现实问题转化为数学问题过程中的思维活动。[8]也就是说,“去情境化”是在情境教学中引导学生从具体情境中抽象出数学问题,并通过数学问题的解决让学生逐渐建构知识的过程。更一般地说,“去情境化”也就是通常所说的“数学化”的一个基本涵义。[7]
2. “数学化”
既然“去情境化”是“数学化”的一个基本涵义,那么对“数学化”的了解将有助于“去情境化”的操作。
“数学化”是弗赖登塔尔数学教育研究所提出的真实数学教育(Realistic Mathematics Education,简称RME)理论的一个核心概念,而弗赖登塔尔(H. Freudenthal)本人也特别强调数学化是数学教育的主题。[9]
所谓的“数学化”就是指人们用数学的方法观察世界,分析研究具体现象并加以组织整理,以发现其中规律的过程;简单地说,数学地组织现实世界的过程就是数学化。[10]更一般地说,数学化是一种由现实问题到数学问题,由具体问题到抽象概念的认知转化活动,是人类发现活动在数学领域的具体表现。[11]在特莱弗斯(Treffers)研究的基础上,弗赖登塔尔将数学化进一步细分为水平数学化与垂直数学化的过程,水平数学化过程是将情境问题表述为具体的数学问题,实现由现实问题向数学问题的转化,是从生活实际走向数学符号世界的过程;垂直数学化过程是将具体问题转化为抽象概念,完成数学问题与数学系统之间关系的建立,是从符号世界过渡到抽象系统的过程。而这两个方向的数学化过程在四个层次[12]中由浅至深地逐渐进行,首先是情境层次(Situation Level),在具体问题情境中促使知识系统化及策略能够得以运用;其次是指涉层次(Referential Level),利用指涉问题所衍生情境的具体数学模型代表特定的数学对象;再次是普遍层次(General Level),使用去脉络化的、具有普遍性的数学模型分析问题程序蕴含的关系;最后是形式层次(Formal Level),在数学范畴内完成对数学对象规范化的步骤和符号进行表述和操作,从而允许学习者进行纯粹思维、反思与欣赏活动。这四个不同的数学化层次的发展,本质上就是从寻求非正式的、与问题情境相关联的结论到一定程度的系统化,再到对隐藏在问题情境背后的一般性原理的深层次理解的过程。[13]
三、启“知”策略探讨
1. 启“知”前,创设情境立足教学任务
数学情境的创设虽是为了引起学生的注意力与学习兴趣、激发学生的学习动机,并在熟悉的、不陌生的情境中产生认知冲突、激起求知欲望,但其主要目的是使学生们在情境中积极主动地发现或提出数学问题,在分析和探究数学问题中建构数学知识。因此,创设的数学情境首先应立足于教学任务,明确教学目标与有序化梳理教材内容,分析学生本阶段的学习特征(如学生的知识经验、学习水平、思维特点与兴趣爱好等),围绕数学核心知识本质,创设利于去情境化的、蕴含数学核心知识概念的、有助于学生习得知识技能与感悟思想方法的、符合学生认知经验的富有趣味性的数学教学情境(如图1所示)。这也就是数学化的第一个层次,创设能够有助于知识系统化及策略能够得以运用的具体问题情境。而精心创设的数学情境问题能够为学生形成非正式的、具有高度特定情境的问题解决策略提供机会;这些非正式的求解过程可能会成为形式化与概括化创造的立足点。[14]
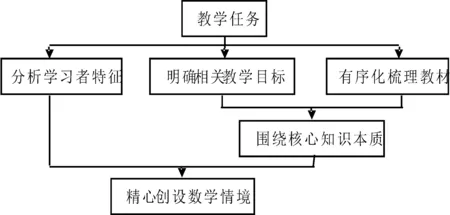
图1 数学情境创设的主要思路
2. 启“知”中,去情境化时渗透数学化思想
数学情境创设之后,要在恰当的时机开始“去情境化”。提出数学问题是去情境化的开始,也是去情境化过程中的一种重要结点。[15]教师需要根据教学任务,高效地引导学生在具体数学情境中形成相关的数学问题意识,再将其表述成文字语言或符号语言,并利用具体的数学模型或适当的图示代表特定的对象,完成从生活实际向数学符号世界转化的水平数学化过程。而提出数学问题时机可以选择在理解的关键处,以促进学生把握知识的重难点、加深理解新知识的本质;也可以选择在认知的冲突处,在学生已有经验的基础上促进学生对知识的迁移及掌握;等等。
接着还要考虑在解决数学问题的过程中实现从符号世界向抽象系统的过渡。所谓的解决数学问题是指学生在新的情境状态下,运用所掌握的数学知识、思想和方法对面临的数学问题采用新的策略和方法以寻求问题答案的一种心理活动过程。[15]这个过程涉及数学化的普遍层次与形式层次,教师需要引导学生要对符号世界中的数学问题模型蕴含的条件与关系进行分析,从非正规的数学解答过渡到在数学范畴内的正规数学解答,完成对数学对象规范化的步骤和符号的表述与操作,从而促使学生上升到对一般性原理深层次理解的过程。
在去情境化中渗透的数学化过程,实际上也是一个逐渐模型化、符号化、概括化、形式化与抽象化的过程,而这几个方面并非孤立地存在着,只有这些方面的整合才能充分发挥数学化思想的价值。[16]特别地,在解决数学问题的过程中,还需进一步揭示问题所涉及的数学思想方法,使学生在启“知”的过程中逐渐怡“情”。
3. 启“知”后,再情境化时注重数学应用
在去情境化中引导学生逐渐加深理解并掌握课堂教学核心知识内容之后,还需通过展示适当的、与教学内容相适应的新情境或新问题,使学生在其中加以巩固与应用所学的新知识与新的思想方法,这是巩固拓展的教学环节,也是再情境化过程。在这个过程中,不仅有助于加深学生对新知的理解与思想方法的感悟,也有助于提高学生应用新知解决数学问题的能力,是从抽象系统返回指导问题解决的过程。
在整合了“数学化”思想在数学问题解决教学中的应用图[13]与情境教学主要流程的基础上,得到了渗透数学化思想的情境教学中各个环节的流程关系(图2)。从中可以看到,启“知”的前、中、后三个环节在情境教学中的环环相扣、地位相当,围绕教学内容的情境化创设能够高效地实施去情境化,渗透数学化思想的去情境化过程能够有助于学生对新知的理解、对数学思想方法的感悟,从而利于再情境化时增强学生应用数学知识与思想方法解决实际生活具体问题的能力。
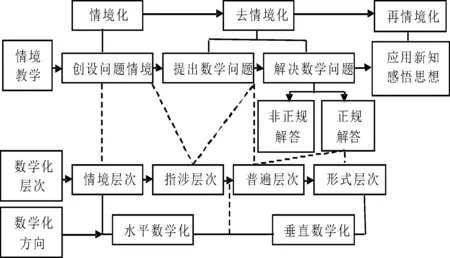
图2 渗透数学化思想的情境教学各个环节的流程关系
四、结语
数学情境教学在实施过程中出现的主要矛盾为情境化与数学化的矛盾,[3]也可以视为情境化与去情境化之间的矛盾。在情境教学过程中,过于偏重情境化的热热闹闹则可能导致数学教学没有了数学味,过于偏重去情境化的理论抽象则可能引起数学教学僵化无趣。我们不应片面地去提倡“数学教学的生活化”,但同时也不应唯一地强调“数学教学的形式化”,也就是说,正确处理“生活数学”与“学校数学”的关系应被看成搞好数学教学的关键所在。[17]经过深思熟虑的情境化与数学化有助于教师确保学生带有真切目标地解决丰富的数学问题;在有意义的情境中引导学生逐渐建构数学工具与原则[18];唯有把握好情境化与去情境化(也即“生活数学”与“学校数学”)之间的平衡,在具体情境中数学化地突出抽象知识,在抽象世界里生活化地理解真实情境,才可能更好地促进学生对抽象知识与思想方法的理解与应用,实现由“境”启“知”到以“知”怡“情”的数学情境教学的目的。
[1] 中华人民共和国教育部.全日制义务教育数学课程标准[M].北京:北京师范大学出版社,2001:1.
[2] 曹新,纪雪颖,张永雪.对数学情境及其性质、作用的探讨[J].课程·教材·教法,2011(1):89-94.
[3] 李三平,朱瑶.简论数学情境教学的认识论基础[J].当代教师教育,2015(4):72-75.
[4] 张玉民.有效教学 聚焦课堂:有效教学情境创设方法.第六卷[M].天津:天津教育出版社,2008:2.
[5] BROWN J. S,COLLINS A , DUGUID P .Situated cognition and the culture of learning[J]. Educational researcher, 1989, 18(1): 32-42.
[6] [美]恰瑞罗特.情境中的课程[M].杨明全,译.北京:中国轻工业出版社,2007,Ⅳ.
[7] 郑毓信.数学教育哲学与课程改革(上)[J].湖南教育(下),2012(2):27-30.
[8] 孙晓天.关于数学基本思想的若干思考[J].江苏教育,2012(34):7-9.
[9] FREUDENTHAL, H . Why to teach mathematics so as to be useful[J]. Educational studies in mathematics, 1968, 1(1): 3-8.
[10] 唐瑞芬,朱成杰.数学教学理论选讲[M].上海:华东师范大学出版社,2000:22.
[11] 孙晓天.现实数学教育的思想基础及其基本概念[J].学科教育,1995(5):16-19.
[12] 张国祥.数学化与数学现实思想[J].数学教育学报,2005(1):35-37.
[13] 孙雪梅,朱维宗.数学化思想及其在数学问题解决教学中的应用分析[J].2010(1):20-22.
[14] DOORMAN M . How to guide students? A reinvention course on modeling motion[J]. Common Sense in Mathematics Education. Proceedings of 2001 The Netherlands and Taiwan Conference on Mathematics Education. Taipei, Taiwan: National Taiwan Normal University, 2002: 97-114.
[15] 潘胜洪.数学情境教学中的去情境化问题初探[J].扬州教育学院学报,2008(3):72-75.
[16] KEIJZER R.Teaching formal mathematics in primary education. Fraction learning as mathematising process[D]. The Netherlands: Utrecht University/Freudenthal Institute, 2003: 16.
[17] 郑毓信.学校数学:必要的抽象[J].人民教育,2006(Z1):43-44.
[18] VAN DEN HEUVEL-PANHUIZEN, M . The didactical use of models in Realistic Mathematics Education: An example from a longitudinal trajectory on percentage[J]. Educational Studies in Mathematics, 2003, 54(1): 9-53.
[责任编辑 张淑霞]
A Discussion about the Strategies of Enlightening Students in Situational Teaching of Mathematics
LI San-ping, GUO Meng-min
(SchoolofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an710119,Shaanxi)
The process of knowledge acquiring is a key link of connecting context and affection in situational teaching of mathematics with the feature of “using context to enlighten students to acquire knowledge, and using knowledge to enlighten students’ affection”,i.e. from the situational questions to the knowledge of questions. The strategies of acquiring effective knowledge include three aspects creating mathematical situations based on teaching tasks, permeating the thinking of mathematization in de-contextualization, and lying emphasis on mathematical applications in re-contextualization.
learning; situational teaching of mathematics; de-contextualization; the thinking of mathematization
2016-08-11
陕西师范大学研究生教育教学改革研究项目(GERP-14-11);陕西师范大学研究生教育教学改革研究项目(GERP-15-40);陕西师范大学第三批信息化课程建设项目
李三平,男,陕西周至人,陕西师范大学数学与信息科学学院副教授;郭梦敏,女,广西南宁人,陕西师范大学数学与信息科学学院硕士研究生。
G642.0
A
1674-2087(2016)03-0056-04

