实对称矩阵的合同
程生敏
(郑州工业应用技术学院基础教学部 河南郑州 451100)
实对称矩阵的合同
程生敏
(郑州工业应用技术学院基础教学部 河南郑州 451100)
关于实对称矩阵的研究有极其广泛的内容,本文主要探讨了实对称矩阵的合同标准形、规范标准形和实对称矩阵的应用等。
实对称矩阵 合同变换 合同标准形
一、预备知识
定义:在数域P中,n n×矩阵A,B称为合同的,若有可逆的n n×矩阵C,使'BC AC=。
二、实对称矩阵的合同标准形、规范标准形等问题
定理1 在数域P上,任意一个实对称矩阵都合同于一对角矩阵,且任一实对称矩阵都合同于一个右边形式的对角矩阵:
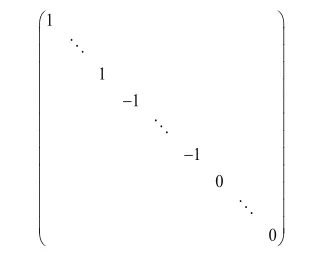
其中对角线上1的个数p及-1的个数rp-(r是A的秩)都是唯一确定的,分别称为A的正、负惯性指数.它们的差2pr-称为A的符号差。
证明:我们对变量的个数n作归纳法。
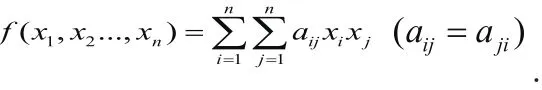
分四种情形来讨论:
(1) aii( i=1,2,...,n)中至少有一个不为零,例如a11≠0.取替换


于是A和C1可写成分块矩阵,
这里'α为α的转置,1nE-为1n-级单位矩阵.这样

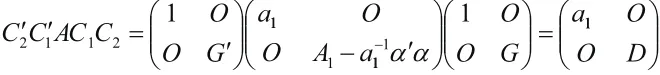
这是一个对角矩阵.我们所要的可逆矩阵就是C=C1C2.
(2) a11=0但有一个aii≠0.
这时只要把A的第一行与第i行互换,再把第一列与i列互换,就归结成上面的情形,根据初等矩阵与初等变换的关系,取

显然P(1,i)'=P(1,i),矩阵就是把A的第一行与第i行互换,再把第一列与第i列互换的结果,因此,C1'AC左上角第一个元素就是aii,这样就归结到第一种情形。
(3) aii=0,i=1,…,n ,但有一a1j≠0,j≠0.
与上一种情形类似,作合同变换P(2,j)'AP(2,j),可以把a1j搬到第一行第二列的位置,这样就变成了配方法中的第二种情况.与那里的变数替换相对应,取C1=,于是的左上角就是
实数域P上,任意实对称矩阵都可以变成规范形,且规范形是唯一的[1]
定理2 实对称阵的特征多项式的根都是实数[1].
定理3 设A是一个实对称矩阵,则属于A的不同特征值的特征向量一定正交[1].
定理4 设是一个n阶实对称阵,总能找到一个n阶正交矩阵P,使P-1AP
为对角阵[1].
由定理4说明,对任何一个实对称阵总有正交矩阵存在,使它化为对角阵,具体如何找到这样的正交矩阵,可按照以下步骤进行:
(2) 对每个λi(i=1,2,…,s).解特征方程组(λiE-A) X=0,找出它们的一个基础解系Xi1,Xi2,…,Xiri,这就是矩阵A的属于特征值λi的线性无关的特征向量;
(3) 用施密特法,将Xi1,Xi2,…,Xiri正交化、单位化,得到一组正交的单位向量组εi1,εi2,…,εiri,它们是A的属于特征值λi的正交的单位特征向量;
(4) 因为λ1, λ2,…,λs各不相同,ε11,…,ε1r1,ε21,…,ε2r2,…,εs1,…,εsrs它们仍是正交的单位向量组,它们的总数为n个,以这一组向量为列,作一个矩阵P,它就是所要求的正交阵.
三、实对称矩阵的应用
若pn=,则该矩阵为正定矩阵;若0pn<<且0q=,则该矩阵为半正定矩阵;
若0pn<<且0qn<<,则该矩阵为不定矩阵;若qn=,则该矩阵为负定矩阵;
若0p=且0qn<<,则该矩阵为负定矩阵.
合同变换除了保秩性外,还具有保定性,利用后一条性质,可把实对称矩阵进行合同分类,实n阶对称矩阵按合同分类,可以分为种,这也就解决了怎样的矩阵是合同的.下面举例看看实对称矩阵及其标准型的应用.
例1 设f( x, y, z)=2y2-8x2-z2-2xy+6xz-2yz,试讨论:若(x, y, z)看作k3上的向量,问在k3上f( x, y, z)是否有非零零点。
解:
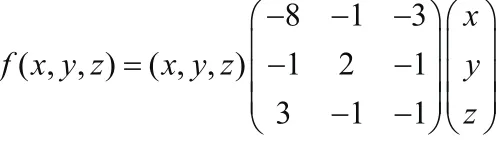
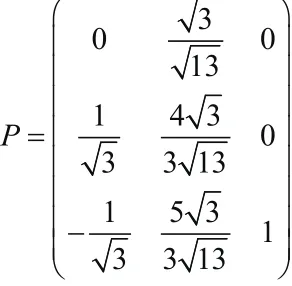
由A是实对称矩阵知A合同于某对角阵,且,
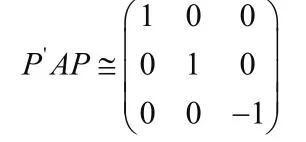
即A为不定阵,由此可得f( x, y, z)在k3上有非零零点.
例2 设A是n阶实对称矩阵,若有n维向量X1,X2,使则必有实n维向量使
证明 因为A为n阶实对称矩阵,所以有n阶可逆矩阵T,使
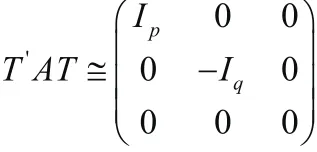
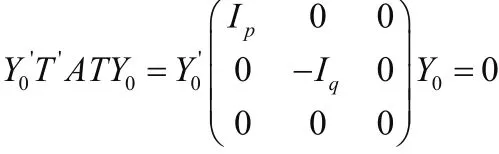
即(TY0)'A( TY0)=0,令X0=TY0,则
例3 设A是一个n阶实对称矩阵,则A是一个秩为r的半正定矩阵⇔存在r个线性无关的实n维列向量αi=(a1i,a2i,...,ani)',i=1,2…,r 使得证明 “⇒”因A是秩为r的半正定矩阵,所以存在n阶实可逆矩阵P,使

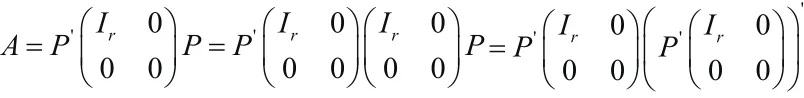
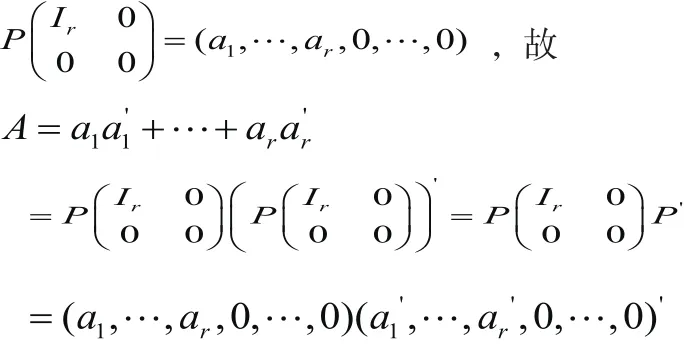
[1] 王萼芳,石生明.高等代数[M].第三版.北京:高等教育出版社,2003.
[2] 陈云龙,钟立敏.线性代数简明方程[M].中国科学技术出版社,1989.
[3] 陈维新.线性代数[M].北京:北京科学出版社,2000.
[4] 孙兰芳,陈一巾.线性代数[M].浙江:浙江大学出版社,1994.
[5] 同济大学应用数学系.高等数学(第五版)[M].北京:高等教育出版社,2001.

