随机环境应力冲击下基于多参数相关退化的导弹部件寿命预测
王浩伟, 滕克难, 李军亮
海军航空工程学院, 烟台 264001
随机环境应力冲击下基于多参数相关退化的导弹部件寿命预测
王浩伟*, 滕克难, 李军亮
海军航空工程学院, 烟台 264001
为了解决某型导弹部件的贮存寿命预测问题,提出了一种随机环境应力冲击下基于多参数相关退化的寿命预测方法。针对产品存在退化失效与突发失效两种失效模式,利用Wiener、Gamma及Inverse Gaussian等随机过程模型拟合各性能参数的退化数据,并采用Copula函数进行相关性退化失效建模;利用随机环境应力冲击解释突发失效的机理,并采用非均匀泊松过程对突发失效建模;进而建立退化失效与突发失效竞争的贮存寿命预测模型。实例应用说明所提方法能够反映出导弹部件的失效规律,比传统预测方法具有更高的预测准确性,具有较好的工程应用价值。
寿命预测; 多参数相关退化; 突发失效; Copula函数; 非均匀泊松过程
准确预测出导弹部件的贮存寿命对有效实施视情维修、提高导弹的作战使用效能具有重要意义。导弹部件失效的根本原因可归结为内部材料性能的下降,例如电阻、电容等老化,电路板焊点发生氧化,机械材料产生腐蚀或裂纹等,如果能掌握导弹部件的性能变化规律,就可预测出其寿命指标[1-4]。
目前,基于性能退化数据的寿命预测方法是一个研究热点[5-6]。文献[7]综述了基于数据驱动的寿命预测方法,文献[8]从基于力学、基于概率统计、基于信息新技术3个方面对机械重大装备的寿命预测方法进行了综述。大多数产品存在多种失效过程,这些失效过程可分为退化失效和突发失效两大类,为了准确预测这些产品的寿命信息,基于竞争失效的寿命预测方法逐渐受到重视。文献[9-12]在处理竞争失效问题时,假定多个失效过程之间不相关,将产品作为一串联系统进行建模。文献[13-14]研究了因为多个参数之间的相关性退化导致产品发生退化失效的情况,采用Copula函数描述了多个参数之间的退化相关性。文献[15]不区分退化失效与突发失效,采用Copula函数描述了多种失效模式之间的相关性。文献[16-20]在考虑退化失效与突发失效相互影响的基础上,研究了竞争失效建模方法。
某导弹部件是典型的机电一体化产品,具有退化失效与突发失效两种失效模式。然而目前对导弹部件寿命预测方法的研究较少,主要难点有两方面。其一,导弹的显著特点为“一次使用,长期贮存”, 一般每半年进行一次定期测试,这有别于其他可以进行实时状态监控的装备,难以获取大量性能退化数据对导弹部件进行寿命预测。其二,导弹部件往往存在多个具有退化趋势的性能参数,合理建立寿命预测模型不但需要考虑多个参数之间的相关性退化问题,而且需要考虑退化失效与突发失效竞争的问题。
为了解决某型导弹部件的贮存寿命预测问题,本文提出了一种随机环境应力冲击下基于多参数相关退化的寿命预测方法。针对产品存在退化失效与突发失效两种失效模式,利用随机过程模型及Copula函数进行相关性退化失效建模,利用随机冲击对突发失效建模,进而建立基于退化失效与突发失效竞争的寿命预测模型,预测出产品的贮存可靠寿命。
1 失效分析与基本假定
导弹部件的退化失效可能由橡胶件老化、润滑剂干涩、结构件疲劳、传动机构磨损、金属件腐蚀、电子件电阻值增大等多种因素造成,导弹是一个由大量部件构成的复杂系统,由于测试时效性要求高,在定期测试时直接测量出每个部件所有的退化量并不现实,可利用获取的测试参数特征电压值表征导弹部件退化程度。当一个或多个测试参数的测量值出现明显的单边或双边变化趋势时,说明导弹部件发生性能退化,当任一个测试参数的测量值达到设定的阈值时,认为导弹部件发生退化失效。
导弹部件的突发失效可认为是由外界应力的随机冲击造成的,例如温度冲击、电应力冲击、振动冲击等。各次随机冲击在时间上是不连续的,如果某次随机冲击达到特定的阈值会造成产品突发失效,称此随机冲击过程称为致命冲击。不造成产品突发失效的随机冲击过程称为非致命冲击,会对导弹部件的多个退化过程产生影响,导致性能退化量发生跃变。
结合以上分析,本文基于以下4点假定建立竞争失效模型:
1) 导弹部件失效是多种退化失效与突发失效竞争的结果。
2) 导弹部件内部的退化相关性表现为多个测试参数的测量值之间具有相关性,并且可以用某种Copula函数表示。
3) 外界应力的非致命随机冲击影响导弹部件的性能退化过程,致命随机冲击造成突发失效。
4) 测试参数的测量值综合表征了此参数正常退化和非致命随机冲击引入的累积退化效果。
2 基于竞争失效的贮存寿命预测模型
对导弹部件的若干次定期测试数据进行分析,设共有m个测试参数的测量值具有单边或双边变化趋势。因为导弹部件所有测试参数的测量时间相对于定期测试间隔期很短,可认为每次定期测试获取的m个测量值在时间上是同步的,t时刻获取的m个测量值可表示为{X1(t),X2(t),…,Xm(t)}。设{D1,D2,…,Dm}为每个测试参数对应的失效阈值,{T1,T2,…,Tm}分别为{X1(t),X2(t),…,Xm(t)}首次到达失效阈值的时刻,则导弹部件在t时刻不发生退化失效的概率为P[X1(t) R(t)=P[T1>t,T2>t,…,Tm>t]× P[N1(t)=0]=P[X1(t) D2,…,Xm(t) (1) 如果{X1(t),X2(t),…,Xm(t)}之间是相互独立的,则式(1)可写为 R(t)=P[X1(t) P[Xm(t) (2) 根据假定2),采用Copula函数描述{X1(t),X2(t),…,Xm(t)}之间的相关性,式(1)可写为 R(t)=C{P[X1(t) P[Xm(t) (3) 利用R(t)可解得可靠寿命、平均寿命等指标。对于此型导弹部件,要求其在贮存期内的可靠度不低于0.9,因此其贮存寿命为可靠度降到0.9的时间点t0.9,即 t0.9=R-1(0.9) (4) 式中:R-1(·)为R(·)的反函数。 由式(3)可知,获得导弹部件的可靠度函数需要分别确定P[X1(t) 由于产品的退化过程具有不确定性和马尔可夫特点,适合利用随机过程进行性能退化建模。Wiener、Gamma和Inverse Gaussian过程是3种典型的连续时间随机过程,其中后两种只能对严格递增或递减退化过程建模。 假定X1(t)服从Wiener退化过程,则可将X1(t)表示为X1(t)=μ·Λ1(t)+σ·B(Λ1(t)),X1(0)=0,Λ1(t)为时间函数并且Λ1(0)=0,μ为漂移参数,σ(σ>0)为扩散参数,B(·)为标准Brown运动函数。平稳独立增量ΔX1(t)服从如下正态分布[21]: ΔX1(t)~N(μΔΛ1(t),σ2ΔΛ1(t)) (5) 式中:ΔX1(t)=X1(t+Δt)-X1(t); ΔΛ1(t)=Λ1(t+Δt)-Λ1(t)。 设性能参数的失效阈值为D1,X1(t)首次到达D1的时间为T1=inf{t|X1(t)≥D1}。根据Wiener过程的统计特性可知T1服从Inverse Gaussian分布,T1的累积分布函数(CDF)为 (6) 假定X2(t)服从Inverse Gaussian过程,则平稳独立增量ΔX2(t)=X2(t+Δt)-X2(t)服从如下形式的Inverse Gaussian分布[22]: ΔX2(t)~IG(δΔΛ2(t),λΔΛ2(t)2) (7) 式中:δ为均值;λ为尺度参数。根据式(7)可推出X2(t)~IG(δΛ2(t),λΛ2(t)2),则X2(t)的概率密度函数(PDF)为 (8) 设D2为失效阈值,则X2(t)首次到达D2的时间为T2={t|X2(t)≥D2},T2的CDF为 FT2(t)=P(T2≤t)=P(X2(t)≥D2)= (9) 假定X3(t)服从Gamma过程,则ΔX3(t)服从如下Gamma分布[23]: ΔX3(t)~Ga(αΔΛ3(t),β) (10) 式中:α为形状参数;β为尺度参数。根据Gamma分布的可加性,得X3(t)~Ga(αΛ3(t),β),X3(t)的CDF表示为 (11) FT3(t)=P(X3(t)≥D3)=1-FX3(D3)= (12) 设总共对导弹部件进行了n次测试,测试时间分别为t1,t2,…,tn,根据式(5)、式(7)和式(10)可分别建立如下极大似然函数,估计出各随机过程的参数值,进而确定出P[X1(t) (13) 式中:Λ1(t)=tr1;Θ1=[μσr1]。 (14) 式中:Λ2(t)=tr2;Θ2=[δλr2]。 exp(-ΔX3(ti)/β) (15) 式中:Λ3(t)=tr3;Θ3=[αβr3]。 利用Copula函数对{X1(t),X2(t),…,Xm(t)}进行相关性建模,为了便于表述,以二元相关退化为例介绍了建模及参数估计方法。表1中以两个相关性变量的情况给出了常用的Copula函数,包括Gaussian、Frank、Gumbel和Clayton 4种类型[13,24]。 设ΔX1(ti)、ΔX2(ti)对应的CDF分别为F1(ΔX1(ti);Θ1)、F2(ΔX2(ti);Θ2),则联合分布函数F(ΔX1(ti),ΔX2(ti);ζ)可写为C(F1(ΔX1(ti);Θ1),F2(ΔX2(ti);Θ2);θ),ζ=[Θ1Θ2θ]。根据Copula函数的性质,联合概率密度函数f(ΔX1(ti),ΔX2(ti);ζ)可表示为 f(Δx1i,Δx2j;ζ)= c[F1(ΔX1(ti);Θ1),F2(ΔX2(ti);Θ2);θ]· f1(ΔX1(ti);Θ1)·f2(ΔX2(ti);Θ2) (16) 式中:c(·)为C(·)对应的概率密度函数。 为了估计出ζ,根据式(16)建立对数似然函数: F2(ΔX2(ti);Θ2);θ)]+ lnf1(ΔX1(ti);Θ1)+lnf2(ΔX2(ti);Θ2)} (17) Copula参数估计方法有全局极大似然 (Full Maximum Likelihood, FML) 法、两步极大似然 (Two-Steps Maximum Likelihood,TSML) 法两类。通过极大化式(17),可以得到全局极大似然估计量为 (18) lnf2(ΔX2(ti);Θ2)] (19) (20) 表1 4种Copula的分布函数和密度函数Table 1 Distribution functions and density functions of 4 kinds of Copula P[X1(t) C{P[X1(t) (21) 设随机冲击服从均匀泊松过程{N(t),t≥0},N(t)代表到t时刻发生随机冲击的次数,发生率记为λ。假定在时刻t1,t2,…,tn发生了随机冲击过程,其随机冲击量分别为{ω(t1),ω(t2),…,ω(tn)},如果随机冲击量ω(ti)达到失效阈值H会造成导弹部件突发失效,则此随机冲击过程为致命冲击。 设在t时刻发生的随机冲击为致命冲击的概率为p(t),则致命冲击服从非均匀泊松过程,发生率记为λp(t)。根据工程经验,在导弹部件的贮存初期发生致命冲击的概率很低,随着贮存时间的增长发生致命冲击的概率变大,因此可设p(t)=1-exp(-γt),γ为参数。综上分析,获得导弹部件在t时刻不发生突发失效的概率为 (22) 因为随机冲击过程发生的时间不连续,目前难以利用现有的技术手段有效检测出其发生时间及随机冲击量,这给参数估计造成了困难。利用同型号导弹部件的历史检测记录可统计出产品的突发失效率随检测时间的变化情况,由式(22)可推导出突发失效率函数为 λ(1-exp(-γt)) (23) 对某导弹每6个月进行一次定期检测,获取了导弹某部件多个测试参数的特征电压值,其中两个测试参数的特征电压值具有退化趋势,分别记为X1(t)和X2(t)。X1(t)的失效阈值为D1=(27±2) V,性能参数X2(t)的失效阈值为D2=(5±0.2) V,X1(t)与X2(t)的总共8组特征电压值如表2所示。 表2 测试参数的特征电压值Table 2 Voltage values of measurement indexes 表3 退化模型参数估计Table 3 Parameter estimates of degradation models 表4 Copula函数参数估计Table 4 Parameter estimates of Copula functions 图1 导弹部件不发生退化失效的概率Fig.1 Non-failure probability of missile component 图2 FX1(D1)和FX2(D2)之间的相关性变化规律Fig.2 Correlative changing rules of FX1(D1) and FX2(D2) 如果只考虑突发失效模式或只考虑退化失效模式,预测出的可靠寿命值如表5所示,可见单纯考虑突发失效或退化失效会造成寿命预测值偏差较大。由于竞争失效模型是突发失效与退化失效的串联关系,在竞争失效情况下所得的寿命预测值比单纯考虑突发失效或退化失效的预测值都要小。 表5 寿命预测结果对比Table 5 Comparison of lifetime prediction results 图3 R1、R2与R3的变化曲线Fig.3 Changing curves of R1,R2 and R3 在考虑竞争失效模式下,设R1为利用本文方法考虑多参数相关退化情况预计的可靠度;R2为利用传统方法假定多参数独立退化预计的可靠度[11];R3为利用同型号导弹部件的真实故障数据评估的可靠度,R1、R2与R3的变化曲线如图3所示。可见R1与R3比较接近,证明本文所提的方法能够较好地预计出产品的寿命指标,而传统方法会造成寿命预测值偏小。 1) 很多部组件级产品发生失效是突发失效和退化失效竞争的结果,只考虑突发失效或退化失效会造成寿命预测值偏大。本文提出的寿命预测方法能够反映出导弹部件的失效规律,比传统预测方法具有更高的预测准确性。 2) 部组件级产品通常具有多个性能退化参数,由于内部结构或功能的相关性,性能参数之间很可能存在退化相关性,假定各退化过程之间相互独立会导致寿命预测值不准确。 3) Copula函数是建立多参数相关退化失效模型的一种有效途径,本文通过测试数据的拟合优劣来确定Copula函数类型,采用二步极大似然法估计未知参数,此多参数相关退化失效建模方法具有较好的工程应用性。 4) 随机环境应力冲击能够较好解释产品突发失效的机理,本文利用非均匀泊松过程描述致命冲击的发生时间从而建立突发失效模型,通过拟合同型号产品历史失效率数据解决了模型参数估计问题。 下一步的理论研究重点是建立数学模型反映出产品退化程度对突发失效概率的影响,工程研究重点是如何有效检测出随机环境应力冲击的时间及冲击量。 [1] 刘震宇, 马小兵, 赵宇. 非恒定温度场合弹上性能退化型部件贮存可靠性评估[J]. 航空学报, 2012, 33(9): 1671-1678. LIU Z Y, MA X B, ZHAO Y. Storage reliability assessment for missile component with degradation failure mode in a temperature varying environment[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1671-1678 (in Chinese). [2] 赵建忠, 叶文, 张磊. 基于数据融合和改进新陈代谢不等间距GM(1,1)模型的导弹装备故障预测[J]. 兵工学报, 2014, 35(10): 1689-1695. ZHAO J Z, YE W, ZHANG L. Failure prediction of missile equipment based on data fusion and AMUGM(1,1) model[J]. Acta Armamentarii, 2014, 35(10): 1689-1695 (in Chinese). [3] 徐廷学. 基于定期检测的导弹贮存可靠性研究[J]. 弹箭与制导学报, 2008, 28(1): 248-250. XU T X. Study on storage reliability based on periodical test for missile[J]. Journal of Projectiles, Rockets, Missile and Guidance, 2008, 28(1): 248-250 (in Chinese). [4] 王浩伟, 徐廷学, 赵建忠. 融合加速退化和现场实测退化数据的剩余寿命预测方法[J]. 航空学报, 2014, 35(12): 3350-3357. WANG H W, XU T X, ZHAO J Z. Residual life prediction method fusing accelerated degradation and field degradation data[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3350-3357 (in Chinese). [5] LOUTAS T H, ROULIAS D, GEORGOULAS G. Remaining useful life estimation in rolling bearings utilizing data-driven probabilistic e-support vectors regression[J]. IEEE Transactions on Reliability, 2013, 62(4): 821-832. [6] LIAO L X. Discovering prognostic features using genetic programming in remaining useful life prediction[J]. IEEE Transactions on Industrial Electrics, 2014, 61(5): 2464-2472. [7] SI X S, WANG W B, HU C H, et al. Remaining useful life estimation—A review on the statistical data driven approaches[J]. European Journal of Operational Research, 2011, 213(1): 1-14. [8] 张小丽, 陈雪峰, 李兵, 等. 机械重大装备寿命预测综述[J]. 机械工程学报, 2011, 47(11): 100-116. ZHANG X L, CHEN X F, LI B, et al. Review of life prediction for mechanical major equipments[J]. Journal of Mechanical Engineering, 2011, 47(11): 100-116 (in Chinese). [9] HUANG W, ASKIN R G. Reliability analysis of electronic devices with multiple competing failure modes involving performance aging degradation[J]. Quality and Reliability Engineering International, 2003, 19(3): 241-254. [10] 张祥坡, 尚建忠, 陈循, 等. 三参数Weibull分布竞争失效场合变应力加速寿命试验统计分析[J]. 兵工学报, 2013, 34(12): 1603-1610. ZHANG X P, SHANG J Z, CHEN X, et al. Statistical inference of varying-stress accelerated life test with competing failures based on three-parameter Weibull distribution[J]. Acta Armamentarii, 2013, 34(12): 1603-1610 (in Chinese). [11] 罗湘勇, 黄小凯. 基于多机理竞争退化的导弹贮存可靠性分析[J]. 北京航空航天大学学报, 2013, 39(5): 701-705. LUO X Y, HUANG X K. Storage reliability analysis of missile based on multi-mechanism competition degradation model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013,39(5): 701-705 (in Chinese). [12] LUO W, ZHANG C H, CHEN X, et al. Accelerated reliability demonstration under competing failure modes[J]. Reliability Engineering and System Safety, 2015, 136: 75-84. [13] PAN Z Q, BALAKRISHNAN N, SUN Q, et al. Bivariate degradation analysis of products based on Wiener processes and copulas[J]. Journal of Statistical Computation and Simulation, 2013, 83(7): 1316-1329. [14] WANG X L, BALAKRISHNAN N, GUO B, et al. Residual life estimation based on bivariate non-stationary gamma degradation process[J]. Journal of Statistical Computation and Simulation, 2015, 85(2): 405-421. [15] YE Z S, TANG L C, XU H Y. A distribution-based systems reliability model under extreme shocks and natural degradation[J]. IEEE Transactions on Reliability, 2011, 60(1): 246-256. [16] ZHANG X P, SHANG J Z, CHEN X, et al. Statistical inference of accelerated life testing with dependent competing failures based on copula theory[J]. IEEE Transactions on Reliability, 2014, 63(3): 764-778. [17] 王华伟, 高军, 吴海桥. 基于竞争失效的航空发动机剩余寿命预测[J]. 机械工程学报, 2014, 50(6): 197-204. WANG H W, GAO J, WU H Q. Residual remaining life prediction based on competing failures for aircraft engines[J]. Journal of Mechanical Engineering, 2014, 50(6): 197-204 (in Chinese). [18] 王浩伟, 奚文骏, 冯玉光. 基于退化失效与突发失效竞争的导弹剩余寿命预测[J]. 航空学报, 2016, 37(4): 1240-1248. WANG H W, XI W J, FENG Y G. Reliability model and evaluation method of products in competing failure modes[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1240-1248 (in Chinese). [19] JIANG L, FENG Q, COIT D W. Reliability and maintenance modeling for dependent competing failure processes with shifting failure thresholds[J]. IEEE Transactions on Reliability, 2012, 61(4): 932-948. [20] WANG Y, PHAM H. Modeling the dependent competing risks with multiple degradation processes and random shock using time-varying copulas[J]. IEEE Transactions on Reliability, 2012, 61(1): 13-22. [21] SI X S, WANG W B, HU C H, et al. A Wiener-process-based degradation model with a recursive filter algorithm for remaining useful life estimation[J]. Mechanical Systems and Signal Processing, 2013, 35(1-2): 219-237. [22] WANG X, XU D. An inverse Gaussian process model for degradation data[J]. Technometrics, 2010, 52(2): 188-197. [23] WANG H W, XU T X, MI Q L. Lifetime prediction based on Gamma processes from accelerated degradation data[J]. Chinese Journal of Aeronautics, 2015, 28(1): 172-179. [24] PAN Z Q, BALAKRISHNAN N. Reliability modeling of degradation of products with multiple performance characteristics based on Gamma processes[J]. Reliability Engineering & System Safety, 2011, 96(8): 949-957. [25] EFRON B. Better bootstrap confidence intervals[J]. Journal of American Statistical Association, 1987, 82(397): 171-185. [26] MARKS C E, GLEN A G, ROBINSON M W, et al. Applying bootstrap methods to system reliability[J]. The American Statistician, 2014, 68(3): 174-180. 王浩伟男, 博士, 讲师。主要研究方向: 装备可靠性评估与寿命预测, 加速试验技术。 Tel: 0535-6635477 E-mail: 13705355730@139.com 滕克难男, 博士, 教授, 博士生导师。主要研究方向: 导弹延寿理论与技术。 E-mail: wyg2010123@126.com *Correspondingauthor.Tel.:0535-6635477E-mail:13705355730@139.com Lifetimepredictionformissilecomponentsbasedonmultipleparameterscorrelativedegradingwithrandomshocksofenvironmentalstresses WANGHaowei*,TENGKe’nan,LIJunliang NavalAeronauticalandAstronauticalUniversity,Yantai264001,China Inordertosolvetheproblemofpredictingthelifetimeofatypeofmissilecomponent,apredictionmethodbasedonmultipleparameterscorrelativedegradingwithrandomshocksisproposed.Theproducthastwofailuremodeswhicharedegradationfailureandtraumaticfailure.Somestochasticprocesses,includingWiener,Gamma,andInverseGaussian,areadoptedtofitthedegradationdataofperformanceindexes,andCopulafunctionsarethenutilizedtomodelthedependentdegradationfailure.Theshocksofrandomenvironmentalstressesareusedtoexplainthemechanismoftraumaticfailure,andanon-homogeneousPoissonprocessisappliedtomodelthetraumaticfailure.Thus,alifetimepredictionmodelissetupbasedoncompetingrisksofdegradationfailureandtraumaticfailure.Anapplicationexamplevalidatesthattheproposedmethod,whichcanmodelthefailuremechanismofthemissilecomponent,possesseshigherpredictionaccuracythantraditionalmethods,andareapplicableinengineering. lifetimeprediction;multipleparameterscorrelativedegrading;traumaticfailure;Copulafunction;non-homogeneousPoissonprocess 2016-01-08;Revised2016-06-01;Accepted2016-06-14;Publishedonline2016-06-201341 URL:www.cnki.net/kcms/detail/11.1929.V.20160620.1341.004.html s:NationalNaturalScienceFoundationofChina(51605487);ChinaPostdoctoralScienceFoundation(2016M592965);ShandongProvinceNaturalScienceFoundation(ZR2016FQ03) 2016-01-08;退修日期2016-06-01;录用日期2016-06-14; < class="emphasis_bold">网络出版时间 时间:2016-06-201341 www.cnki.net/kcms/detail/11.1929.V.20160620.1341.004.html 国家自然科学基金 (51605487); 中国博士后科学基金 (2016M592965); 山东省自然科学基金 (ZR2016FQ03) * .Tel.:0535-6635477E-mail13705355730@139.com 王浩伟, 滕克难, 李军亮. 随机环境应力冲击下基于多参数相关退化的导弹部件寿命预测J. 航空学报,2016,37(11):3404-3412.WANGHW,TENGKN,LIJL.LifetimepredictionformissilecomponentsbasedonmultipleparameterscorrelativedegradingwithrandomshocksofenvironmentalstressesJ.ActaAeronauticaetAstronauticaSinica,2016,37(11):3404-3412. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0192 TJ761.1; TB114.3 A 1000-6893(2016)11-3404-093 退化失效建模
3.1 性能退化建模





3.2 相关性建模





4 突发失效建模


5 案例应用



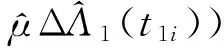






6 结 论

