多指标约束下考虑报废的可修复备件携行方案优化

刘任洋， 李庆民， 李华， 熊宏锦

1. 海军工程大学 兵器工程系， 武汉 4300332. 海军工程大学 科研部， 武汉 4300333. 海军装备部驻重庆地区军事代表局，重庆 400042

多指标约束下考虑报废的可修复备件携行方案优化

刘任洋1， 李庆民2, *， 李华1， 熊宏锦3

1. 海军工程大学 兵器工程系， 武汉 4300332. 海军工程大学 科研部， 武汉 4300333. 海军装备部驻重庆地区军事代表局，重庆 400042

针对任务期间普遍存在的故障件报废和备件多指标约束问题，提出了多层级装备的可用度近似评估方法及携行备件方案优化方法。首先通过忽略维修时间将考虑报废率的多层级可修件转化为单层级消耗件，进而利用伽马分布的可加性建立装备可用度评估模型。在此基础上以装备可用度、备件总质量为约束指标，以备件总体积最低为目标构建多约束备件优化模型。模型求解过程中引入拉格朗日因子，并采用边际算法对约束因子进行动态调整。算例中通过与仿真结果的对比、分析得出：当维修时间取值在部件等效平均寿命的一半以内时，提出的近似方法合理可行，平均误差小于5%。

任务期间； 多指标约束； 报废率； 可用度； 备件方案

装备在执行任务期间，备件方案的优化问题往往受多个指标的制约。例如，飞机在作战准备阶段，飞行基地需要携带配套备件以保证一定周期内的独立作战。由于受携行能力、空间等条件的限制，对配套备件种类和数量的确定不仅要考虑装备可用度等战备完好性指标，还需要综合考虑备件的质量、体积、数量规模等因素。在该情况下，需要在满足装备可用度等各项指标的约束下，寻找最为合适的备件携行方案。因此，在装备使用阶段针对特定应用背景开展多指标约束下的备件优化问题具有现实意义。

国内外学者针对多约束备件优化问题开展了一系列的研究。Bachman和Kline[1]、Robert和Tovey[2-3]在备件质量、体积、期望短缺数等多指标约束下，对航空备件的配置优化问题进行研究；卫忠等[4]建立了多级库存控制下协同供应链的多目标优化模型，并采用遗传算法对模型进行求解。各项指标权重在模型优化迭代计算过程中动态更新，以得到满足各项指标约束的备件优化方案[5-6]；王乃超和康锐[7]建立了单层级装备的多约束库存优化模型，并利用次梯度法更新拉格朗日乘子求得模型最优解；阮旻智等[8]针对各约束指标之间的不同量纲范围，解决了模型中初始约束因子的确定问题。

然而，以上文献的研究对象均针对消耗件或完全可修件，而当飞机在执行具体任务时，受现场维修条件制约，飞行基地不可能对所有故障情况进行修复，必然有一批故障件会因为得不到修复而报废[9]。因此，当故障件存在报废率时，其备件模型如何建立是一个值得研究的问题。

本文针对上述问题，在飞行基地无外界补给的特定保障模式下，结合任务期间修复概率小于1的实际情况，利用近似等效思想建立了装备可用度近似评估模型以及多指标约束下的携行备件方案优化模型。在算例中通过仿真方法验证了本文模型的有效性和适用性，并分析了多约束指标值的设定范围。研究内容可为装备保障人员在任务期间对装备保障效能的评估、多约束指标值的设定以及备件方案的制定提供新思路。

1 模型描述及参数定义

1.1 模型描述与假设

装备一般包含多个结构层次，根据在装备系统所处的不同结构层次，备件分为现场可更换单元(Line Replacable Unit，LRU)、车间更换单元(Shop Replacable Unit，SRU)等，图1为一个典型的多层次结构系统。

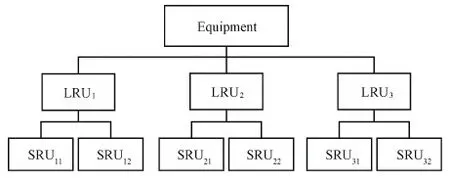
图1 装备层次结构Fig. 1 Hierarchical structure of equipment

下面以装备中包含LRU、SRU为例，描述其维修保障过程。在任务周期内，若装备发生故障，原因是所属的第1层级部件LRU故障导致，采用换件维修的方式将故障LRU拆卸。如果现场有该LRU备件，则立刻进行更换完成装备的修理，如果没有LRU备件，就发生一次LRU备件短缺。受维修条件限制，拆下的故障LRU存在一定的修复概率，如果不能维修则报废。对故障LRU进行维修，故障原因是其所属的SRU故障导致。如果现场有该SRU备件，则将其安装到LRU上从而完成对LRU的修理，如果没有SRU备件，则会造成LRU的修理延误。故障SRU的维修和报废过程与LRU相同。当一件LRU修理成功，备件短缺事件就得以解决[10]。

为了简化建模过程，在上述保障过程描述的基础上做出如下几点假设和说明：

1) 所有备件需求率均服从泊松分布。

2) 故障件的定位以及备件的更换在瞬间完成，时间均忽略不计。

3) 对故障件维修时不考虑故障单元之间的维修优先权，采用先到先维修的策略，不考虑重测完好率、虚警率等维修参数的影响。

4) 现场维修渠道无限，不会因为维修渠道被占满而出现维修等待的现象。

5) LRU的故障只是由于其所属SRU之一故障所致，不考虑多个SRU同时故障的情况。

6) 部件均存在一定的修复概率，无法维修则报废，不考虑外部补给的情况。

7) 部署于飞机上的多台同型装备之间为独立关系，工作时相互不受影响；装备中同一层级部件之间为串联关系。

1.2 重要参数定义及符号说明

i：部件项目编号，i=1,2,…,I，I为部件类型总数。

c：部件层级编号，c=0,1,…,C，c=0表示装备系统，c=1表示第1层级部件LRU，c=C表示处于装备中最底层部件；c=2,3,…,C-1表示处于中间结构层级部件；

Inden(c)：在装备结构中处于第c层次的项目集合。

Sub(i)：部件i所属下一层级的分组件集合。

Aub(i)：部件i上面所有层级的母体集合。

MTBFi：部件i的平均寿命。

ri：部件i的维修概率。

Zi：部件i在其母体中的单机安装数量。

Si：备件i的库存量。

mi：备件i的质量。

vi：备件i的体积。

T：装备在任务周期内的计划工作时间。

N：装备在飞机上的部署数量。

A：装备可用度。

2 考虑报废的多层级可修件近似等效模型

2.1 报废条件下可修件的消耗件近似等效

对于存在一定报废概率的可修件，从其工作到报废的整个寿命周期看，除了中间的若干次维修过程，与消耗件存在相似的寿命过程。两者的本质区别在于前者是间断工作直至报废，而消耗件是连续工作直至报废。间断工作的原因由维修造成，通过分析可知：维修时间对备件模型的本质影响是产生维修延误，而维修延误在很多情况下都会被充足的备件抵消或降低。因此，为了便于建模和工程应用，本节提出忽略维修时间，将间断工作的可修件等效为连续工作的消耗件处理。

对于单项可修件，在任务时间周期内发生故障的平均次数为

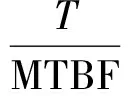
(1)

在不考虑维修时间的条件下，可将该可修件近似等效为平均寿命为MTBFe的消耗件，其中MTBFe即首项为MTBF，公比为r，项数为n(对n取整)的等比数列之和：

MTBFe=MTBF+MTBF·r+

MTBF·r2+···+MTBF·rn-1=

(2)

式(2)描述了任务期间在一定维修概率下，可修件经历若干次故障、维修以及正常工作的寿命周期过程。通过上述寿命等效过程，具有维修概率r，平均故障间隔时间为MTBF的可修件则近似等效为平均寿命为MTBFe的消耗件。而对于忽略维修时间的可行性和误差分析，将在后面的算例中进行讨论。

2.2 多层级备件的单层级等效

由多层级装备的维修过程可知，由于下层级的子备件完全用于维修故障的母体部件，使母体部件产生新的备件，因此若能提前算出所有下层子备件所能维修的对应故障母体部件的总数量，就能将该母体部件的维修总量作为母体备件去代替所有下层级的子备件。即将下层级的子备件数量折算成上层级的母体备件数量，实现装备多层级的扁平化处理。

对于底层部件i(i∈Inden(C))，利用2.1节方法将其等效为消耗件，考虑机装数和上面所有层级母体部件l(l∈Aub(i))维修概率的影响，等效后的平均寿命为

(3)

等效消耗件备件数量为底层部件i的原始备件数量：

Sei=Si

(4)

对于中间层级部件i(i∉Inden(C),i∉Inden(1))，当部件i发生故障，其故障原因是所属的某个子部件z(z∈Sub(i))故障所致的条件概率为

(5)

则对故障部件i维修一次所消耗子备件z的数量为

(6)

将所有子备件消耗量等效折算为部件i的备件增加量，即

(7)

下面给出部件i累积备件增加量的计算流程：

步骤3更新当前各子备件库存量：Sz=Sz-ΔSz,z∈Sub(i)。

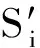
(8)

通过以上折算过程，将部件i等效为消耗件，其平均寿命为

(9)

对于顶层部件LRUi(i∈Inden(1))，其等效备件数量和平均寿命的计算过程与中间层级部件相同，但由于考虑装备部署数量，由式(8)计算得到的等效备件数量还需要在各装备之间平均分配。因此，对式(8)进行修正得到顶层部件LRUi(i∈Inden(1))的等效备件数量为

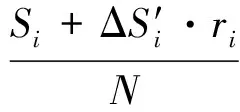
(10)

其等效平均寿命则由式(9)得到。

装备组成中各层级部件的等效备件数量和等效平均寿命均可根据上述步骤进行递推，递推计算由底层部件i(i∈Inden(C))开始，直至顶层部件(第1层级LRU)，从而将复杂的多层级备件问题转换为只需考虑第1层级LRUi(i∈Inden(1))的单层级消耗件问题。

3 可用度评估模型

装备可用度是评价备件方案好坏、评估装备保障效能的常用指标，其定义为装备期望工作时间与总任务时间之比。由第2节方法计算得到的顶层LRUi等效备件数量Sei(i∈Inden(1))通常为非整数，直接利用指数型可用度计算模型将面临备件数量的近似取整问题，从而会导致一定的误差。由伽马分布的性质可知，指数分布是伽马分布的特例，利用这一性质，可将指数型部件转化为伽马型部件处理。

对于服从Ga(a,b)的伽马分布，当a=1时，伽马分布即为指数分布。因此，平均寿命为MTBFei(i∈Inden(1))的指数型LRU部件与参数为(1,MTBFei)的伽马型LRU部件完全等效。根据伽马分布的可加性[11]：服从参数(1,MTBFei)的伽马型LRU部件，忽略备件更换时间，在Sei次换件下的寿命仍服从伽马分布，其参数为(1+Sei,MTBFei)，这里形状参数1+Sei可以取值非整数，很好地避免了指数型备件数量需近似取整的问题。由此得到LRUi在Sei个备件下的可靠度函数为

(11)

由于假设装备各LRU组件为串联的可靠性关系，对于串联系统可用度的求解，大部分参考文献及资料均认为系统(装备)可用度为各LRU可用度之积，如颇具权威性的GJB4355[12]以及METRIC理论的相关经典文献和著作[13-14]，即

(12)

实际上，用式(12)计算串联系统可用度是不准确的。因为对于串联系统而言，只存在系统可靠度为各部件可靠度之积这一性质：

(13)

由于装备可用度为任务时间内的平均可靠度[15]，则有

(14)

对比式(12)、式(14)，显然有A≥A′，因而对于串联系统，用单元可用度之积去计算系统可用度将导致结果偏低，从而得到保守的备件方案。

4 多指标约束下的备件方案优化模型

4.1 优化模型的建立

在规划任务期间空运携行备件方案时，受飞机携行能力及空间的制约，备件方案的制定常常受到多项指标因素的约束，除了装备可用度约束外，还有备件质量、体积等。因此，建立备件优化模型时需要对这些指标进行综合权衡，在满足各项指标的同时使备件方案达到最优。所建优化模型为

(15)

式中：M0为规定的总质量指标；A0为规定的可用度指标。

4.2 模型的求解方法

通过引入拉格朗日乘子处理上述多指标约束问题[3]，将备件的单位质量约束转化为体积约束，得到包含备件质量和体积的资源规模为

di=vi+θmmi

(16)

式中：θm为拉格朗日质量因子。采用边际优化算法[16]对模型进行求解，在确定边际效应值时，用备件资源规模约束di代替只考虑体积约束的vi，具体步骤如下：

步骤1构造备件方案矩阵S=[S1S2…SI]，并初始化令S=0。

步骤2计算第i项备件的边际效应值为

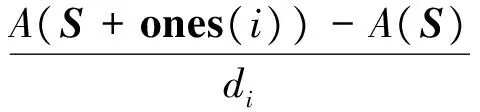
(17)

式中：ones(i)为第i项备件库存量为1，其他全为0的矩阵。

步骤3将δ(i)值最大者所对应的备件i库存量加1，由此得到新的库存量矩阵S。

步骤4计算在新库存方案S下的装备可用度A，并与规定的可用度指标A0比较，如果A≥A0，算法结束，此时的S即为最优备件方案；反之则转入步骤 2进行迭代。

由于拉格朗日因子θm在上述求解过称中为未知参数，因此，在模型优化前首先需要确定θm的值，方法如下：

步骤1令θm=0，通过上述边际优化算法得到只考虑体积约束下的备件方案矩阵S0。

步骤2计算在该方案下的备件总质量M(S0)和总体积V(S0)。

步骤3确定θm的初始值，记为θm0：

θm0=V(S0)/M(S0)

(18)

步骤4计算在θm0下的备件方案矩阵S以及对应的M(S)和V(S)。

步骤5如果满足M(S)≤M0，算法结束，S即为最优方案。如果M(S)>M0，说明备件方案未满足质量指标要求，需要增大θm的值，其增量确定方法为

(19)

得到调整后的θm值后转入步骤 4。

需要指出的是，由于各指标之间的相互制约，可能存在不论怎么调整θm0的值都得不到满足所有约束指标的备件方案，此时则需要考虑适当放宽约束条件。

5 算例分析

5.1 案例想定

假设某飞行装备执行空中侦察任务，任务期间计划总工作时间T=1 500 h。装备的层次结构如图1所示，部署数量N=1。装备所含部件均存在一定修复概率。现要求制定该装备的配套备件携行方案，使装备可用度不低于0.95，备件总质量不高于460 kg。备件的相关输入参数如表1所示(Ti为部件i的维修时间)。

表1 备件输入参数Table 1 Input parameters of spare parts

5.2 携行备件方案优化结果与仿真验证

为了验证本文近似可用度评估方法的正确性，采用MATLAB平台构造仿真模型与近似结果进行对比。仿真次数设为1 000，单次仿真的主要流程如图3所示，分别统计每次仿真的累计停机时间Td，则可用度为1-Td/T，取1 000次仿真所得的可用度均值作为最终输出结果。将表2的备件携行方案输入仿真模型，得到装备可用度评估结果为0.931 9，与仿真结果相比，近似结果的相对误差为2.64%，在合理的误差范围内。

表2 最优备件携行方案Table 2 Optimal carrying project of spare parts

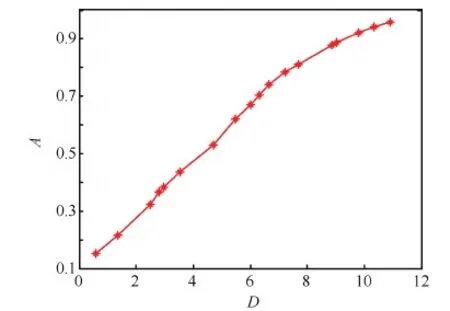
图2 多指标约束下的备件优化曲线 Fig. 2 Optimization curve of spare parts under multi-constraints

图3 单次仿真的主要流程Fig. 3 Main simulation process of single time

5.3 多约束指标值设定分析

在设置多约束指标值时，由于各指标间的相互制约，如果指标值设置不合理，模型则无法求解。实际上，对于本文的多约束问题，当其中一个约束指标值确定后，其他约束指标均存在在该指标约束值下的上限值，只有当其他约束指标设定的规定值不超过它们各自的上限值，才有可能求出满足条件的最优解。因此，通过求解其他指标的上限值可以判断规定的约束指标值是否设置合理，也可以为各指标值的设定提供参考。

以可用度达到0.95为约束指标，计算质量和体积指标的上限值。方法为分别以备件总质量最小、备件总体积最小为优化目标，利用单指标的边际优化算法，得到如图4所示的优化迭代曲线。所得质量指标的上限值为458 kg，体积指标的上限值为3 m3。因此，要使可用度达到0.95，在设置质量或体积的指标值M0、V0时，应尽量满足M0≥458 kg，V0≥3 m3。

图4 不同优化目标下的迭代曲线Fig. 4 Iteration curves under different optimization objective

5.4 近似方法适用性分析

为了探究本文近似方法的适用性以及维修时间Ti对可用度评估的影响。在表2所求最优备件方案S下，令任务周期计划工作时间T以500 h为间隔，在[1 000,10 000] h区间内取值，比较近似方法与仿真方法的可用度评估结果如图5(a)所示，图中两条曲线基本重合，相对误差最大发生在T=3 000 h时，其值为3.12%，在合理范围内。由此可以看出，相对于漫长的任务期，算例中由80 h的维修时间产生的维修延误时间(即由于故障件维修或等待维修造成的装备停机时间)极短甚至可以忽略不计，从而对可用度的影响不大。

图5 不同维修时间下的可用度评估结果对比 Fig. 5 Comparison of availability results at different maintenance time

将所有部件的维修时间进一步延长，分别设为150 h、300 h，得到近似结果和仿真结果如图5(b)和图5(c)所示。同图5(a)进行综合对比可以看出，随着维修时间的增加，近似评估曲线逐渐偏离仿真曲线，近似结果相对误差最大值分别增加至5.86%和8.79%。这是由于维修时间的增加造成维修延误的逐渐累积，当维修延误时间累积增加到一定程度时将对可用度造成较大影响。

通过大量试验表明，当维修时间取值在部件等效平均寿命的一半以内时，本文近似评估方法能保证一定的精度(平均误差5%以内)；当维修时间超过部件等效平均寿命时，近似方法无法实现定量评估，但可以作为定性评估备件方案好坏和可用度高低的有效手段。另外，作为一种工程近似的解析方法，其对可用度的评估耗时仅为仿真方法的十分之一，在面对大批量备件优化问题时具有一定优势。

6 结 论

本文结合任务期间普遍存在的故障件报废问题，研究了多指标约束下携行备件方案的优化方法，并对各约束指标值的设定范围进行了分析。通过与大量仿真结果的对比验证表明：本文近似可用度评估方法能对维修时间不是太长(在部件等效平均寿命的一半以内)的一般情况进行较准确的定量评估，平均误差在5%以内，且维修时间越短，精度越高。

[1] BACHMAN T C, KLINE R C. Model for estimating spare parts requireents for future missions: AIAA-2004-5978[R].Reston: AIAA, 2004.

[2] ROBERT C K, TOVEY C. Estimating spare parts requirements with commonality and redundancy: AIAA-2006-7233 [R]. Reston: AIAA, 2006.

[3] ROBERT C K, TOVEY C. Estimating spare parts requirements with commonality and redundancy[J]. Journal of Spacecraft and Rockets, 2007, 44(4): 977-984.

[4] 卫忠, 徐晓飞, 战德臣, 等. 协同供应链多级库存控制的多目标优化模型及其求解方法[J]. 自动化学报, 2007, 33(2): 181-187.

WEI Z, XU X F, ZHAN D C, et al. Multi objective optimization model for collaborative multi-echelon inventory control in supply chain[J]. Acta Automatica Sinica, 2007, 33(2): 181-187 (in Chinese).

[5] LI Y, YANG B, HU H J. A simulation-optimization approach to spare parts allocation based on decision-maker’s satisfaction[C]//Proceedings of International Conference on Reliability Maintainability and Safety, 2009: 576-581.

[6] IMAN N, SEYED R H. A multi-objective approach to simultaneous determination of spare part numbers and preventive replacement times[J]. Applied Mathematical Modeling, 2011, 35: 1157-1166.

[7] 王乃超, 康锐. 多约束条件下备件库存优化模型及分解算法[J] . 兵工学报, 2009, 30(2): 247-251.

WANG N C, KANG R. An optimization model for inventory spares under multi-constraints and its decomposition algorithm[J]. Acta Armamentarii, 2009, 30(2): 247-251 (in Chinese).

[8] 阮旻智, 李庆民, 张光宇, 等. 多约束下舰船装备携行备件保障方案优化研究[J]. 兵工学报, 2013, 34(9): 1144-1149.

RUAN M Z, LI Q M, ZHANG G Y, et al. Optimization method of carrying spare parts support project for warship equipment under multi-constrants[J]. Acta Armamentarii, 2013, 34(9): 1144-1149 (in Chinese).

[9] RUAN M Z, LUO Y, LI H. Configuration model of partial repairable spares under batching ordering policy on inventory state[J]. Chinese Journal of Aeronautics, 2014, 27(3): 558-567.

[10] FRANCESCO C, GIULIO D G, MASSIMO T. Multi-echelon, multi-indenture spare parts inventory control subject to system availability and budget constraints[J]. Reliability Engineering and System Safety, 2013, 119: 95-101.

[11] 甘茂治, 康建设, 高崎. 军用装备维修工程学[M] .第2版. 北京：国防工业出版社, 2010: 42-46.

GAN M Z, KANG J S, GAO Q. Military equipment maintenance engineering[M].2nd ed. Beijing: National Defense Industry Press, 2010: 42-46(in Chinese).

[12] 中国人民解放军总装备部. GJB4355-2002 备件供应规划要求[S]. 北京： 中国人民解放军总装备部， 2003: 21-22.

The PLA General Armament Department. GJB4355-2002 Spares provisioning requirements[S]. Beijing: The PLA General Armament Department, 2003: 21-22 (in Chinese).

[13] SHERBROOKE C C. VARI-METRIC: Improved approximations for multi-indenture multi-echelon availability models[J]. Operations Research, 1986,34: 311-319.

[14] SHERBROOKE C C. Optimal inventory modeling of system: Multi-Echelon techniques[M]. 2nd ed. Boston: Artech House, 2004: 29-31.

[15] 王慎. 装备使用阶段备件保障策略优化及仿真建模方法研究[D]. 武汉: 海军工程大学, 2014: 30-31.

WANG S. Research on optimization and simulation modeling method for support policies of spare parts in operational phase of equipments[D]. Wuhan: Naval University of Engineering, 2014: 30-31 (in Chinese).

[16] 刘任洋, 李庆民, 李华. 基于横向转运策略的可修件三级库存优化模型[J]. 航空学报, 2014, 35(12): 3341-3349.

LIU R Y, LI Q M, LI H. Optimal model of three-echelon inventory for repairable spare parts with lateral transshipments[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3341-3349 (in Chinese).

刘任洋男，博士研究生。主要研究方向：装备综合保障。

E-mail: 463572090@qq.com

李庆民男，博士，教授，博士生导师。主要研究方向：装备综合保障仿真技术，海军水中兵器对抗仿真与试验等。

Tel: 027-83442947

E-mail: licheng001@hotmail.com

李华男，博士，高级工程师。主要研究方向：装备综合保障仿真技术，海军水中兵器对抗仿真与试验等。

E-mail: akbng094nba@163.com

熊宏锦男，博士。主要研究方向：装备保障和维护。

E-mail: andy_sto@163.com

URL：www.cnki.net/kcms/detail/11.1929.V.20160118.1642.012.html

Optimizationmethodofcarryingprojectforrepairablespareswithscrapundermulti-constraints

LIURenyang1,LIQingmin2,*,LIHua1,XIONGHongjin3

1.DepartmentofWeaponryEngineering,NavalUniversityofEngineering,Wuhan430033,China2.OfficeofResearch&Development,NavalUniversityofEngineering,Wuhan430033,China3.MilitaryRepresentativeOfficeofNavalEquipmentDepartmentinChongqing,Chongqing400042,China

Forthewidelyexistedproblemofthescrapforfaultpartsandsparescarryingundermulti-constraintsduringthemission,approximationmethodofavailabilityevaluationandsparesoptimizationformulti-indentureequipmentareproposed.First,repairablespareswithscrapwhichcontainmulti-indentureareconvertedtonon-repairablespareswhichonlycontainsingle-indenturebyomittingthemaintenancetime.Then,evaluationmodelofavailabilityisobtainedbasedontheadditivepropertyofGammadistribution.Afterwards,theoptimizationmodelofsparesisbuiltwiththelowestvolumeunderconstraintsofavailabilityandmass.Lagrangefactorstowhichdynamicadjustmentismadebymarginalalgorithmareintroducedduringthemodelsolving.Inactualexamplecomparedwithsimulationresults,theapproximationmethodisreasonableandfeasiblewhenmaintenancetimeislessthanhalfoftheequivalentaveragelife,whichmakestheaverageerrorlessthan5%.

duringthemission;multi-constraints;scraprate;availability;sparepartconfiguration

2015-10-29;Revised2015-11-19;Accepted2016-01-04;Publishedonline2016-01-181642

s：NationalDefensePre-researchFoundationofChina(51304010206,51327020105)

.Tel.:027-83442947E-maillicheng001@hotmail.com

2015-10-29;退修日期2015-11-19;录用日期2016-01-04; < class="emphasis_bold">网络出版时间

时间:2016-01-181642

www.cnki.net/kcms/detail/11.1929.V.20160118.1642.012.html

国防预研项目 (51304010206，51327020105)

.Tel.:027-83442947E-maillicheng001@hotmail.com

刘任洋， 李庆民， 李华， 等．多指标约束下考虑报废的可修复备件携行方案优化J. 航空学报,2016,37(10):3131-3139.LIURY,LIQM,LIH,etal.Optimizationmethodofcarryingprojectforrepairablespareswithscrapundermulti-constraintsJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3131-3139.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0018

V125.7 ; E911； TJ761.1

A

1000-6893(2016)10-3131-09