非旋转钝锥高超声速自由飞非线性角运动轨迹重构与分析

蒋增辉， 宋威， 鲁伟， 陈农

中国航天空气动力技术研究院， 北京 100074

非旋转钝锥高超声速自由飞非线性角运动轨迹重构与分析

蒋增辉*， 宋威， 鲁伟， 陈农

中国航天空气动力技术研究院， 北京 100074

采用多阶段曲线拟合技术，对双平面拍摄风洞自由飞试验获得的高超声速下非旋转钝锥角运动观测值作了拟合，获得了与试验观测值重合度较好的拟合曲线，进而实现了对试验模型非线性角运动轨迹的重构，获得了5次试验的复攻角和总攻角曲线，并进而对非旋转钝锥非线性角运动的特点和规律进行了分析。结果分析表明：模型复攻角曲线可能逆时针方向转动也可能顺时针方向转动，甚至可能改变转动方向；复攻角曲线多呈“椭”圆锥运动，且椭圆运动的长轴在大小和方向上均可能发生变化；总攻角幅值呈振荡变化，但多呈总体上减小的趋势；由于角运动的非线性特性，同样的试验模型在不同的预置攻角情况下其角运动特性也呈现出很大的不同。

非线性角运动； 轨迹重构； 复攻角； 总攻角； 自由飞； 高超声速

弹箭在飞行中的角运动对其飞行特性具有较大影响[1], 对弹箭的角运动规律作深入透彻的分析，有助于研究弹箭的运动规律，对于角运动非线性较为强烈的情况尤为重要[2-5]。

风洞自由飞试验是研究弹箭角运动规律的一个有效方法，其可通过高速摄影的拍摄，直接获得弹箭的角位移曲线。考虑到旋转弹箭的自由飞行运动存在较强烈的俯仰和偏航方向运动耦合作用的影响，为了较为直观地描述弹箭的角运动规律，通常对旋转弹箭模型的风洞自由飞试验进行双平面拍摄，并对其两个方向的角运动规律如复攻角曲线图进行重构拟合[6-14]，以直观地观察其角运动的轨迹规律。而非旋转钝锥的风洞自由飞试验以往通常都是简化为平面运动来处理[15-20]，忽略另一方向运动的影响，因此通常只拍摄记录其俯仰平面的运动规律，偏航平面的角运动均被忽略，因而未见到有文献对其两个方向的总的角运动轨迹规律进行分析。

而在笔者开展的非旋转钝锥双平面拍摄高超声速风洞自由飞试验中，却发现试验中的非旋转钝锥均出现了较为明显的圆锥摆动，在观察窗范围内的侧滑角幅值均大于攻角幅值，对试验结果的初步分析发现两个方向的角运动非线性均较为强烈，因此此时若仍按以往的简化处理方法，忽略其中一个平面的运动将难以真实反映非旋转钝锥的角运动规律，因而需对其两个方向的角运动规律均进行研究，进而对其两个方向的角运动轨迹均进行重构才能进一步对其角运动规律进行研究。由于角运动非线性较为明显，使得采用基于线性理论的三周期法获得的拟合曲线与观测值曲线存在较大偏差[21]，二者重合性较差，因此线性理论无法实现对钝锥的实际角运动轨迹进行较好的拟合，对其出现的圆锥摆动的复攻角及总攻角曲线也无法进行重构。

采用分段拟合技术可实现获得非旋转钝锥在小攻角高超声速下气动导数非线性的具体形式及其小攻角下的非线性运动特点[22]，但由于无法获得对观测值曲线的直接拟合，因而仍然无法获得直观描述钝锥非线性角运动轨迹的曲线，使得对试验过程中的模型实际的非线性角运动轨迹变化和规律仍缺乏直观的印象和认识。

本文采用多阶段曲线拟合技术对双平面拍摄获得的高超声速非旋转钝锥风洞自由飞试验的角运动观测值作非线性的拟合，对其角运动轨迹进行重构，以期获得较为直观的描述其高超声速自由飞行过程中的非线性角运动曲线，进而实现对其非线性角运动特点的分析。

1 非旋转弹箭非线性角运动拟合方法

Beyers[23]提出了一种非线性角运动的近似拟合方法，也即多阶段曲线拟合技术(Multi-Stage Curve Fitting Procedure)，其基本思想是，首先采用线性拟合方法对试验获得的角运动数据进行拟合，进而对角运动残差再采用线性拟合公式进行拟合，以此类推。最后，将各次拟合所获得的角运动数据叠加，即可获得较为接近弹箭实际非线性运动的拟合曲线，即

α=α1+α2+α3+…+αn

(1)

其中α1即为在整个角运动中贡献最大的线性解，其方程即为非旋转弹箭平面运动的三周期法方程：

α1=k1eλ1cos(ω1t+φ1)+c1

(2)

式中：k1为初始振幅；λ1为阻尼指数；ω1为角频率；t为时间；φ1为初始相位；c1为小不对称项。

而α2，α3，…，αn均为与之形式相同的三周期法方程，只是其中的参数与线性形式的方程式(2)是不同的。

式(1)和式(2)均为攻角平面的非线性角运动拟合方程，同理可获得侧滑角平面的非线性角运动拟合方程为

β=β1+β2+β3+…+βn

(3)

且有

βj=kjeλjcos(ωjt+φj)+cj

(4)

由于风洞自由飞试验可以较方便地获得俯仰角θ和偏航角ψ，且其分别与攻角α和侧滑角β近似相等，因此可用俯仰角θ和偏航角ψ来代替式(1)～式(4)中的攻角α和侧滑角β。

2 非线性角运动重构与分析

图1和图2分别为在中国航天空气动力技术研究院FD-07风洞中进行的10° 半锥角非旋转钝锥高超声速(马赫数Ma=6)双平面拍摄风洞自由飞试验结果，图中拟合曲线均为采用线性理论得到。可以看到，线性拟合得到的两次试验α-t曲线和β-t曲线均与原始试验数据曲线存在较大偏差，二者重合性较差，尤其是曲线的峰值处，有较多不重合且存在较大差异之处。因此若采用线性理论来重构复攻角及总攻角曲线图将存在较大的误差，难以获得其真实的角运动轨迹。

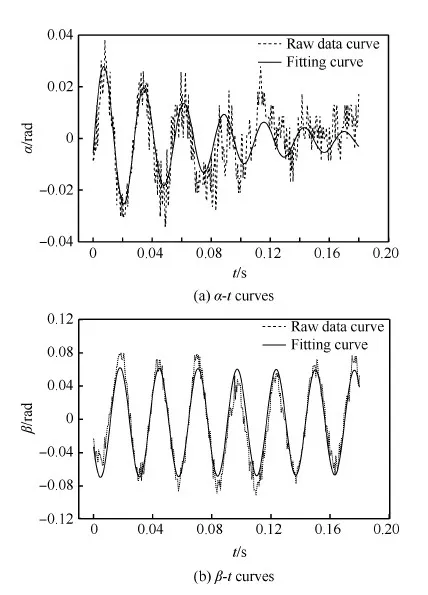
图1 线性拟合得到的第1组试验角运动曲线 Fig.1 Angular motion curves of the first test by linear fitting

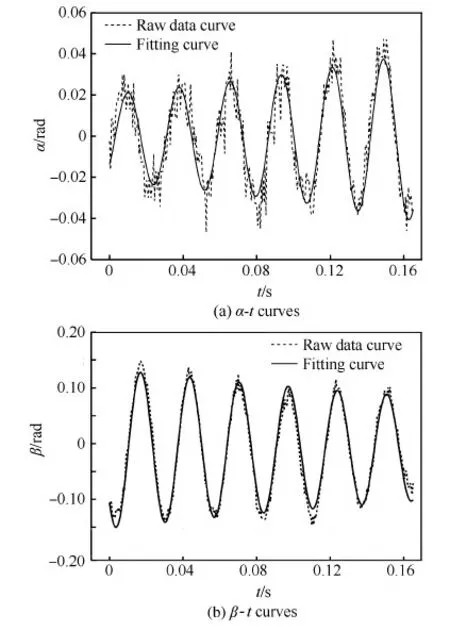
图2 线性拟合得到的第2组试验角运动曲线Fig.2 Angular motion curves of the second test by linear fitting

图5和图6即为采用上述非线性拟合曲线的数据得到的两次试验的复攻角曲线α-β图和总攻角αtotal-t曲线。可以看到，复攻角α-β图将模型在试验中其攻角和侧滑角轨迹的变化发展过程完全展现了出来，从图中可以很直观地看出，两次试验中，复攻角α-β图均呈逆时针方向转动，且侧滑角振荡的幅值在试验记录的区域内始终明显大于攻角振荡的幅值，因此模型在这段时间内实际上是在作着逆时针转动的“椭”圆锥运动。图5所示的试验由于攻角幅值的振荡迅速衰减，而侧滑角幅值则无明显变化，因此复攻角α-β图显示了其呈现由“椭”圆锥运动逐渐向平面(侧滑角平面)振荡运动变化的发展过程，且在这一过程中，椭圆的长轴沿顺时针方向旋转；图6中的复攻角α-β图则显示模型的角运动始终呈现“椭”圆锥运动，且椭圆长轴也呈顺时针方向旋转的，并且长轴呈现逐渐减小的趋势，而短轴变化趋势则不甚明显，这些运动变化趋势导致了攻角振荡幅值的逐渐增大和与之同步的侧滑角振荡幅值的逐渐衰减的趋势。

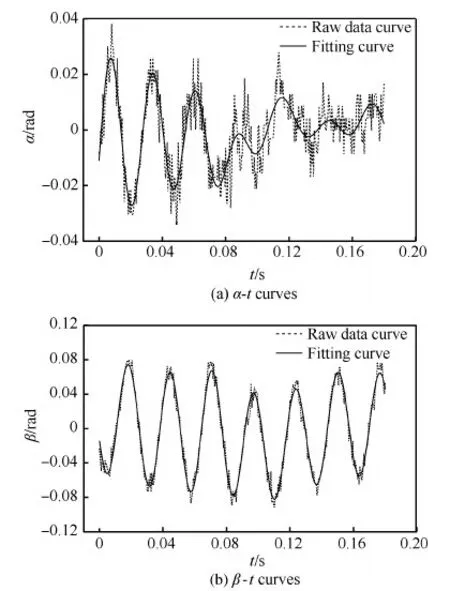
图3 非线性拟合得到的第1组试验角运动曲线Fig.3 Angular motion curves of the first test by nonlinear fitting

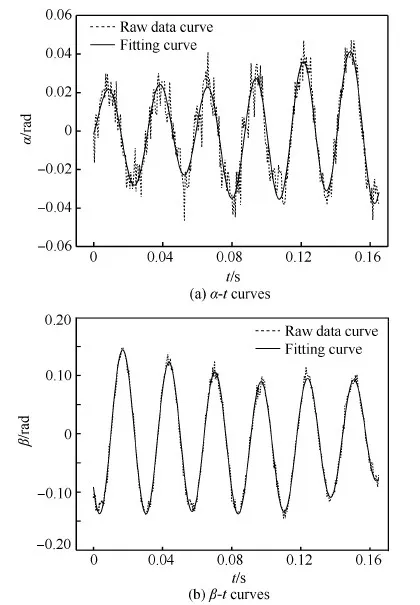
图4 非线性拟合得到的第2组试验角运动曲线Fig.4 Angular motion curves of the second test by nonlinear fitting

图5(b)和图6(b)所示的αtotal-t曲线显示，尽管总攻角幅值振荡变化，但两次试验的总攻角幅值总体上还是呈现减小的趋势，尤其是第2次试验(图6(b))总攻角幅值的减小在整个试验过程中都较为明显，整体上处于持续的衰减状态。需注意的是，由于攻角和侧滑角的相位相差π/2，因此总攻角幅值并不是与攻角和侧滑角幅值的简单叠加。

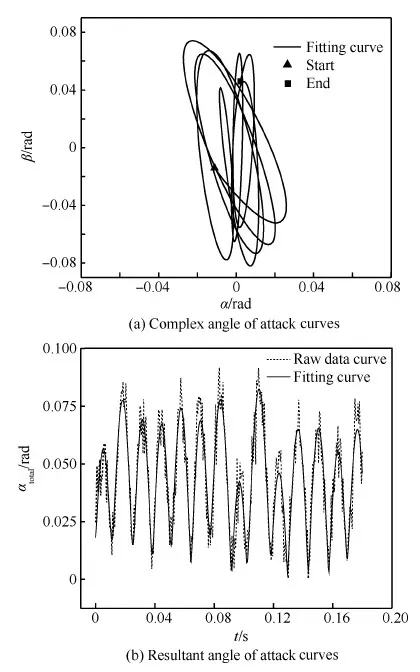
图5 第1组试验复攻角和总攻角曲线 Fig.5 Complex angle of attack and resultant angle of attack curves of the first test

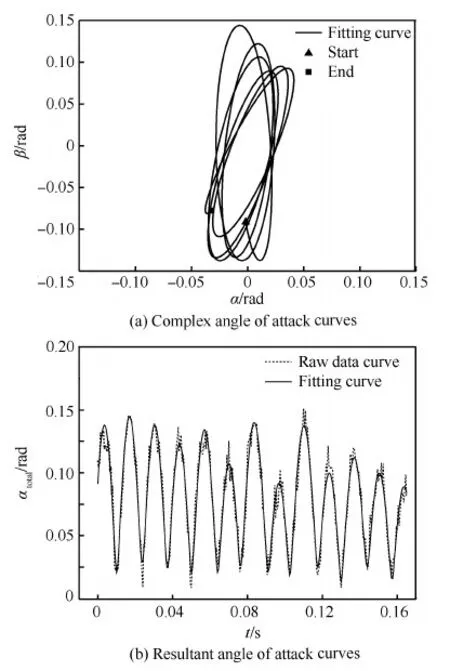
图6 第2组试验复攻角和总攻角曲线 Fig.6 Complex angle of attack and resultant angle of attack curves of the second test

上述两次试验均是在预置3° 攻角和0° 侧滑角的情况下进行的，模型有所区别，分别为尾部带端盖和尾部不带端盖但加了片条状凸起物的10° 半锥角钝锥(模型具体外型见文献[21])

与上述两次试验同时开展的还有3次非旋转钝锥自由飞试验，与上述两次试验相同，这3次试验两个方向的角运动残差也是连续作了4次拟合，也即方程中的n均为5。3次试验的两个方向角运动曲线也均得到了较好的拟合，由于做上述非线性拟合的主要目的是为了得到复攻角和总攻角曲线，因此为简化描述，本文不再给出上述试验的α-t和β-t曲线，而是直接给出这3次试验的非线性拟合复攻角和总攻角曲线，如图7～图9所示。3次试验的马赫数与上述两次试验相同，只是对模型或试验工况作了调整。其中1次的试验模型与第1次试验(图5)相同，只是初始预置攻角为2°，其复攻角和总攻角曲线如图7所示；另外两次试验仍为3° 预置攻角，只是试验模型分别为既带端盖又加片条状凸起物，以及既无端盖又无片条状凸起物的钝锥模型(模型具体外形见文献[21])其复攻角和总攻角曲线分别如图8和9所示。

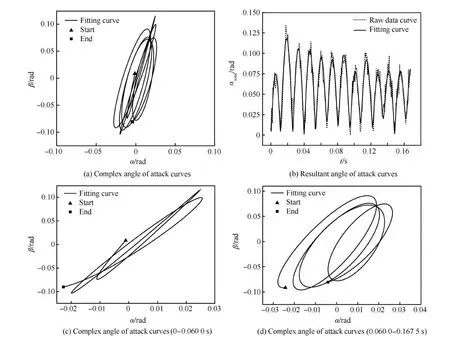
图7 第3组试验复攻角和总攻角曲线Fig.7 Complex angle of attack and resultant angle of attack curves of the third test

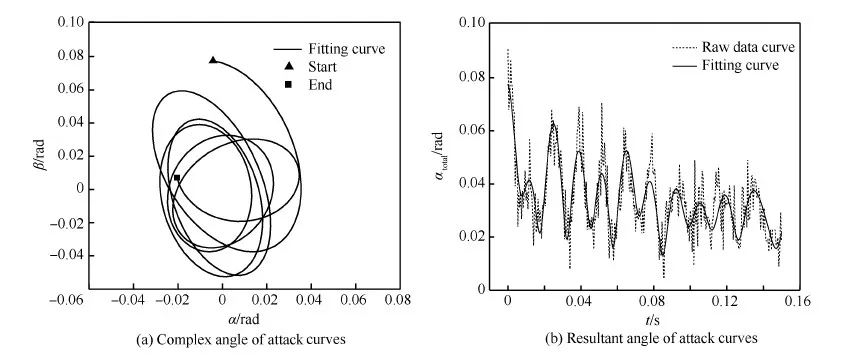
图8 第4组试验复攻角和总攻角曲线Fig.8 Complex angle of attack and resultant angle of attack curves of the fourth test

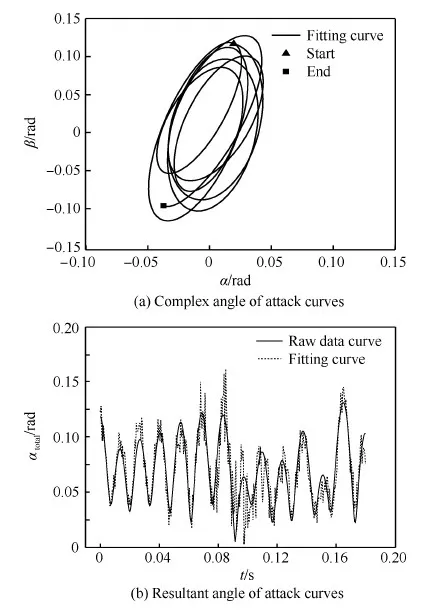
图9 第5组试验复攻角和总攻角曲线 Fig.9 Complex angle of attack and resultant angle of attack curves of the fifth test

图7～图9中的复攻角曲线显示3次试验的复攻角曲线也均呈“椭”圆锥运动。其中图7(a)所示的无片条状凸起物也无端盖的钝锥模型复攻角曲线显示，曲线呈逆时针方向转动一圈后转为顺时针方向转动，其后一直保持顺时针转动；椭圆的长轴逐渐减小，短轴在刚刚转为顺时针转动时先迅速增大，再呈略有减小的趋势。复攻角曲线呈现长轴方向没有发生旋转的“椭”圆锥运动。为清楚地描述转动的变化过程，将整个试验过程的复攻角曲线分为两段分别给出，如图7(c)和图7(d)所示。图7(b)所示的总攻角曲线显示，总攻角幅值总体上呈减小的趋势，且总攻角幅值在曲线的后4个周期似已衰减至进入接近恒定值。本次试验与第1次试验仅为预置攻角的不同，但复攻角曲线虽有一定相似性，却也显示出较大的不同，这也说明了角运动的非线性特性。

图8(a)和图9(a)所示的复攻角曲线均呈顺时针方向的转动，这与前面3组试验均不相同。同时，图8(a)所示的既有片条状凸起物也有尾端盖的钝锥模型复攻角曲线显示，模型在最初几周作长轴没有发生旋转的“椭”圆锥运动后，其长轴迅速衰减至与短轴差距较小，且长轴由侧滑角方向迅速转为攻角方向的运动状态；图9(a)所示的既无片条状凸起物又无尾端盖的钝锥模型复攻角曲线则显示模型呈现长轴方向一直没有发生旋转的“椭”圆锥运动，且长轴和短轴的大小也没有明显变化，因此复攻角形态呈形状无明显变化的“椭”圆锥运动。

图8(b)所示的总攻角曲线呈现幅值明显衰减的趋势，且在振荡运动的最后5周总攻角幅值似已有渐趋恒定的趋势；图9(b)所示的总攻角曲线则呈现幅值处于较为剧烈的振荡过程，无明显趋势。

综上，5次试验的复攻角曲线中，有2次试验中模型复攻角α-β曲线图呈逆时针方向转动，2次则是呈顺时针方向转动，还有1次则是先逆时针方向转动1圈后转为顺时针方向转动，其后一直保持顺时针方向转动。

四是，引入“中国梦”宣传教育可以提高为大学生营造一个良好的学习氛围。众所周知，大学生在成长过程中经常会受到环境的影响，在环境影响下，大学生的思想、情感都会产生变化，不利于成长。而在大学思想政治教育中引入“中国梦”宣传教育可以提高为大学生营造一个良好的学习氛围，对教学环境进行创新，优化人文环境，让大学生在良好的人文环境中，提高人文素养，学会明辨是非，树立正确人生价值观，潜移默化中推动社会主义文化快速发展，满足大学生成长需求。

5次试验的复攻角曲线均呈“椭”圆锥运动，所不同的是1次试验呈现由“椭”圆锥运动逐渐向平面(侧滑角平面)振荡运动变化的发展过程，其他4次则一直呈“椭”圆锥运动。但这4次作“椭”圆锥运动的试验中又有3次试验复攻角曲线的长轴呈减小趋势，另1次长轴没有明显变化；而短轴除1次试验有大小的波动外，其余均无明显变化。

5次试验中，有2次试验的椭圆长轴呈现沿顺时针方向旋转的状态，2次试验的椭圆长轴方向一直没有发生旋转，另1次试验的椭圆长轴在最初几周没有发生旋转，随后长轴由侧滑角方向迅速转为攻角方向。

尽管总攻角幅值均呈振荡变化，但5次试验中的4次试验总攻角幅值总体上仍呈现出减小的趋势，其中有2次的总攻角幅值在曲线的后几个周期似已衰减至渐趋恒定的趋势。只有1次试验的总攻角曲线呈现幅值处于较为剧烈的振荡过程，无明显趋势。

由于角运动的非线性特性，同样的试验模型在不同的预置攻角情况下其角运动特性也呈现出很大的不同。

上述5次试验中复攻角和总攻角曲线所呈现出的复杂特征，表明非旋转钝锥模型角运动的较为复杂的特性，且上述角运动特性规律及其中某些较为独特的运动规律与贴片、加盖等局部特征的添加并无明显的对应的关系。

3 结 论

本文采用的多阶段曲线拟合技术实现了对双平面拍摄风洞自由飞试验获得的高超声速下非旋转钝锥角运动观测值较好的非线性拟合，实现了对其角运动轨迹的重构，获得了5次试验的复攻角和总攻角曲线，进而对非旋转钝锥非线性角运动进行了分析。研究结果表明：

1) 模型复攻角α-β曲线图的转动方向可能逆时针方向转动也可能顺时针方向转动，甚至可能改变转动方向。

2) 复攻角曲线多呈“椭”圆锥运动，且存在向平面振荡运动变化发展的可能；椭圆运动的长轴在大小和方向上均可能发生变化。

3) 总攻角幅值呈振荡变化，但多呈总体上减小的趋势，且在曲线的后几个周期可能呈现衰减至渐趋恒定的趋势。

4) 由于角运动的非线性特性，同样的试验模型在不同的预置攻角情况下其角运动特性也呈现出很大的不同。

高超声速下非旋转钝锥角运动所展现的上述复杂特性，需开展进一步的研究工作，以分析和探讨其产生的机理和规律。

[1] 林献武, 王中原, 王天明, 等. 高空环境下超远程火箭的角运动模型[J]. 飞行力学， 2009， 27(5)： 66-69.

LIN X W, WANG Z Y, WANG T M, et al. Angular motion models for ultra range rocket in high altitude environment[J]. Flight Dynamics, 2009, 27(5): 66-69 (in Chinese).

[2] 李臣明. 高空气象与气动力对远程弹箭弹道影响的研究[D]. 南京： 南京理工大学, 2007: 72-115.

LI C M. The study on ballistic influence of meteorology and aerodynamic force for long-range shells and rockets under high altitude[D]. Nanjing: Nanjing University of Science and Technology, 2007: 72-115 (in Chinese).

[3] 邓超. 弹箭非线性角运动规律研究[D]. 南京： 南京理工大学， 2013: 40-76.

DENG C. Research about the regular pattern of nonlinear angualar movement of projectile[D]. Nanjing: Nanjing University of Science and Technology, 2013:40-76 (in Chinese).

[4] 韩子鹏. 弹箭外弹道学[M]. 北京： 北京理工大学出版社, 2008: 281-313.

HAN Z P. Exterior ballistics of projectiles and rockets[M]. Beijing: Beijing Institute of Technology Press, 2008: 281-313 (in Chinese).

[5] 李奉昌, 韩子鹏. 弹丸非线性运动理论[M]. 北京： 机械委兵工教材编审室, 1988: 93-215.

LI F C, HAN Z P. The nonliear motion theory of projectiles[M]. Beijing: The Read and Edit Room of Ordnance Industry of Mechanism Committee, 1988: 93-215 (in Chinese).

[6] 蒋增辉， 陈农. 旋转钝锥双平面拍摄风洞自由飞试验[J]. 力学学报, 2013， 45(5): 777-781.

JIANG Z H, CHEN N. Wind tunnel free-flight test with biplanar optical system on the spinning blunt cone[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 777-781 (in Chinese).

[7] PRISLIN R H, HOLWAY H P. A wind tunnel free flight testing technique for nonplanar motion of spinning models: AIAA-1966-0774[R]. Reston: AIAA, 1966.

[8] JAFFE P. Nonplanar tests using the wind-tunnel free-flight technique[J]. Journal Spacecraft, 1973, 10(7): 435-442.

[9] INGRAM C W, NICOLAIDES J D. Obtaining nonlinear aerodynamic stability coefficients from free-angular motion of rigid bodies[J]. Journal Spacecraft, 1969, 8(4): 390-395.

[10] NICOLAIDES J D, EIKENBERRY R S, INGRAM C W, et al. Flight dynamics of the basic finner in various degrees of freedom: AFATL-TR-68-32[R]. Indiana: University of Notre Dame, 1968.

[11] NICOLAIDES J D, EIKENBERRY R S, INGRAM C W, et al. Nonlinear aerodynamic characteristics of re-entry configurations with aerodynamic and mass asymmetries: AIAA-1969-0867[R]. Reston: AIAA, 1969.

[12] NICOLAIDES J D, INGRAM C W, CLARE T A. Investigation of the nonlinear flight dynamics of ordnance weapons[J]. Spacecraft, 1970, 7(10): 1241-1243.

[13] LUSARDI R J, NICOLAIDES J D. The determination of non-symmetric aerodynamics of re-entry missiles: AIAA-1974-0108[R]. Reston: AIAA, 1974.

[14] HODAPP A E Jr. Effects of unsymmetrical stability derivative characteristics on re-entry vehicle transient angular motion[J]. Spacecraft, 1975, 13(4): 82-90.

[15] LEWIS H O, EAST R A. Measurement of free-flight dynamic stability derivatives of cones in a hypersonic gun tunnel: AIAA-1995-6082[R]. Reston: AIAA, 1995.

[16] PRISLIN R H. High-amplitude dynamic-stability characteristics of blunt 10-degree cones: AIAA-1966-0465[R]. Reston: AIAA, 1966.

[17] NICOLAIDES J D, INGRAM C W, MARTIN J M. Nonlinear aerodynamic stability characteristics of the 2.75 wrap-around fin configuration[C]//Procedings of the 8th Navy Symposium on Aeroballistics. Corona, CA: Naval Weapons Center, 1969, 3: 751-832.

[18] EIKENBERRY R S. Analysis of the angular motion of missiles: SC-CR-70-6051[R]. Indiana: University of Notre Dame, 1970.

[19] 马家驩, 唐宗衡, 张小平, 等. 激波管风洞中锥模型静、动稳定性导数的测量[J]. 力学学报, 1980, 16(1): 84-89.

MA J H, TANG Z H, ZHANG X P, et al. The measurements of the static and dynamic stability derivatives of conical models in the shock tunnel[J]. Chinese Journal of Theoretical and Applied Mechanics, 1980, 16(1): 84-89 (in Chinese).

[20] 许可法, 何龙德, 李明娟, 等. 大攻角风洞自由飞动导数实验研究[J]. 航空学报, 1993, 14(8): B394-B397.

XU K F, HE L D, LI M J, et al. Experimental investigation of dynamic stability derivatives at high angle of attack in wind tunnel free-flight[J]. Acta Aeronautica et Astronautica Sinica, 1993, 14(8): B394-B397 (in Chinese).

[21] 蒋增辉, 宋威, 陈农. 非旋转钝锥高超声速双平面拍摄风洞自由飞试验[J]. 力学学报, 2015, 47(3): 406-413.

JIANG Z H, SONG W， CHEN N. Hypersonic wind tunnel free-flight test with biplanar optical system on the non-spinning blunt cone[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(3): 406-413 (in Chinese).

[22] 蒋增辉, 宋威, 陈农. 小迎角高超声速非旋转钝锥非线性运动分析[J]. 航空学报, 2016, 37(5): 1454-1461.

JIANG Z H, SONG W，CHEN N. Analysis of nonlinear motion for hypersonic non-spinning blunt cones at small angle of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1454-1461 (in Chinese).

[23] BEYERS M E. A new technique for the analysis of non-linear free-flight motion： AIAA-1974-0614[R]. Reston: AIAA, 1974.

蒋增辉男， 博士， 高级工程师。主要研究方向： 非定常空气动力学、 超空泡流体动力学。

Tel: 010-68376792

E-mail: jzhhit@163.com

宋威男， 硕士， 助理工程师。主要研究方向： 非定常空气动力学。

Tel: 010-68376792

E-mail: 623426297@qq.com

鲁伟男， 硕士研究生。主要研究方向： 非定常空气动力学。

Tel: 010-68376792

E-mail: 851074070@qq.com

陈农男， 博士， 研究员。主要研究方向： 非定常空气动力学。

Tel: 010-68741250

E-mail: chennong27@126.com

URL：www.cnki.net/kcms/detail/11.1929.V.20160329.1529.006.html

Trajectoryreconstructionandanalysisofnonlinearangularmotionofhypersonicfree-flightnon-spinningcones

JIANGZenghui*,SONGWei,LUWei,CHENNong

ChinaAcademyofAerospaceAerodynamics,Beijing100074,China

Employingmulti-stagecurvefittingprocedure,theobservationsofhypersonicnon-spinningbluntconeswind-tunnelfree-flighttestswithbiplanaropticalsystemareanalyzedbynonlinearfitting.Perfectcoincidenceisacquiredbetweenthefittingcurvesandobservations,andthentrajectoryreconstructionofthenonlinearangularmotionofthemodelsisachieved.Complexangleofattackandresultantangleofattackcurvesareobtainedforfivetests,andthenthecharacteristicsofthenonlinearangularmotionofthenon-spinningbluntconesareanalyzed.Therotatingdirectionofcomplexangleofattackcurvesisuncertain,andbothclockwiseandanticlockwisearepresent,sometimesthereisevenachangeinrotatingdirection.Mostcomplexangleofattackcurvespresentellipticalconemotion,andthemagnitudeanddirectionofthelongaxisofellipseareprobablyvariable.Themagnitudeofresultantangleofattackdecreasesingeneral,thoughitisoscillatory.Duetothenonlinearcharacteristics,differentcharacteristicsexistfortheangularmotionwithidenticalmodelatdifferentpresetanglesofattack.

nonlinearangularmotion;trajectoryreconstruction;complexangleofattack;resultantangleofattack;free-flight;hypersonic

2015-11-18；Revised2015-12-08；Accepted2016-03-14；Publishedonline2016-03-291529

NationalNaturalScienceFoundationofChina(11202200)

.Tel.：010-68376792E-mailjzhhit@163.com

2015-11-18；退修日期2015-12-08；录用日期2016-03-14； < class="emphasis_bold">网络出版时

时:2016-03-291529

www.cnki.net/kcms/detail/11.1929.V.20160329.1529.006.html

国家自然科学基金 (11202200)

.Tel.：010-68376792E-mailjzhhit@163.com

蒋增辉， 宋威， 鲁伟， 等． 非旋转钝锥高超声速自由飞非线性角运动轨迹重构与分析J． 航空学报,2016,37(10):2932-2940.JIANGZH,SONGW,LUW,etal.Trajectoryreconstructionandanalysisofnonlinearangularmotionofhypersonicfree-flightnon-spinningconesJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):2932-2940.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0088

V211.7； V212.1

A

1000-6893(2016)10-2932-09