鲁棒的结构网格自动化重叠方法

王文， 阎超,*， 袁武， 黄宇， 席柯

1.北京航空航天大学 航空科学与工程学院， 北京 100083 2.中国科学院 计算机网络信息中心 超级计算中心, 北京 100190 3.中国兵器工业导航与控制技术研究所, 北京 100089

鲁棒的结构网格自动化重叠方法

王文1， 阎超1,*， 袁武2， 黄宇1， 席柯3

1.北京航空航天大学 航空科学与工程学院， 北京 100083 2.中国科学院 计算机网络信息中心 超级计算中心, 北京 100190 3.中国兵器工业导航与控制技术研究所, 北京 100089

网格技术是目前数值模拟中的关键技术之一。重叠网格是一种放宽拓扑要求、减小网格生成难度的网格技术。本文以结构重叠网格为基础，分别针对挖洞、寻点以及洞面优化方法进行了研究和改进，同时完成物面网格重叠，形成了一套鲁棒的、自动化的网格重叠系统。在挖洞方面，结合“最小洞映射”方法，提出“复合式挖洞”方法，节省内存开销；在寻点方面，通过构建格心虚网格，保证搜索空间的连续性，同时结合“有效搜索”思想，排除部分对寻点无贡献的网格点，进而减少ADT叉树节点；在洞面优化上，改变填补判别法则并引入两类受保护洞内点，确保两层插值边界建立，提高鲁棒性；在物面网格重叠上，利用物面投影法完成坐标修正，实现物面附近网格流动变量的准确传递。为验证本文方法，分别对定常翼身组合体DLR-F6绕流和非定常机翼挂载分离过程进行了数值模拟，计算结果与实验结果吻合良好，表明该结构重叠网格系统对多物体间定常、非定常扰流具有较好的数值模拟能力和较高的模拟精度，具有较高的工程应用价值。

计算流体力学； 结构重叠网格； 洞映射； 寻点； 洞面优化方法； 翼身组合体； 机翼挂载分离

随着人类对航空航天飞行器性能的不断追求，近几十年来航空航天技术有了突飞猛进的发展，与此同时，飞行器的构型越来越复杂，并且经常伴随着相对运动，典型的例子有：高升力体外形(High-lift Configuration)升阻力预测[1]、外挂物与载机分离过程[2]、固体火箭助推器与航天飞机分离[3]、子母弹抛撒过程[4]、直升机旋翼运动[5]等。在单个或者多个复杂构型数值模拟过程中，网格生成技术是关键技术之一，网格质量的好坏直接影响CFD计算结果的精度。因此，如何快速地、高质量地生成网格成为了目前CFD技术中亟待解决的问题之一。

目前处理复杂构型的网格主要包括：结构网格、非结构网格和混合网格。结构网格由于数据结构简单、计算技术成熟、计算效率和计算精度较高以及黏性模拟能力强等优点而被广泛应用，但复杂构型飞行器生成一体化结构网格仍然显得十分困难，且不易保证网格质量，有时简单构型物体组合在一起，空间拓扑也会变得异常复杂。与此同时，刚性的结构网格也无法处理有较大相对运动的情况。为降低结构网格生成难度，Steger等[6]在20世纪80年代提出了重叠网格(Chimera Grids)方法。重叠网格也称为覆盖网格(Overlapping Grids)或嵌套网格(Overset Grids)，它是将计算区域划分成多个独立的子区域，各子区域网格随部件作刚性运动，流场信息在网格重叠部分通过插值进行传递。重叠网格放宽了网格拓扑要求，极大降低了网格生成难度，提高了网格质量，因此得到了大力的发展和广泛的应用，同时涌现出一大批著名的软件，如Pegasus5[7]、Overgrid[8]、Suggar[9]等。国内对重叠网格的研究起步相对较晚，但发展十分迅猛，在工程领域也得到逐步应用。如陈十一等[10]采用结构重叠网格技术，利用壁面约束的大涡模拟(CLES)、分离涡模拟(DES)以及雷诺平均Navier-Stokes(RANS)方法对商用飞机进行全机数值模拟；曹义华等[11]采用结构重叠网格对带旋翼的直升机进行了数值模拟并对空间数值格式进行评价；蔡晋生等[12]发展了一种多层多块隐式嵌套重叠网格技术并对翼身平尾组合体进行了数值模拟与分析；田书玲等[13-15]开展了基于非结构网格方法的动态重叠网格算法研究。

本文主要是对现有的结构重叠网格技术进行研究，提出了鲁棒的重叠方法，主要包括4个方面：① 完善洞映射方法，提出“复合式挖洞”方法，节省内存开销；② 提出“有效搜索”思想，提高寻点效率；③ 将混合洞面优化方法推广至非定常多体运动数值模拟中，并引入两类受保护洞内点，提高鲁棒性；④ 采用物面投影法对物面附近重叠网格进行坐标修正，保证流动变量在物面附近正确传递。最后，选取翼身组合体DLR-F6扰流和机翼挂载分离算例对本重叠网格技术的性能进行了检验和验证。

1 挖洞方法

挖洞是重叠网格需要进行的第1步操作，目的是在流场计算前屏蔽掉一些不必要或者无实际意义的点，如落入物面、对称面或人为指定曲面内的点，并将其标记为“洞内点”，以区别于参与流场计算的“洞外点”，也称为“正常点”。网格域内，区分“洞内点”和“洞外点”的界线称为“洞边界”。常见的挖洞方法有点矢法[16]、射线求交法[17]、洞映射法[18]、X射线(Object X-Rays)法[19]、叉树法[20]、直接法[21]、隐式切割(Implicit Hole Cutting， IHC)法[22]等，本文选取发展较为成熟、使用灵活的洞映射法为挖洞方法。

洞映射方法将曲物面投射到辅助的直角笛卡儿网格中，得到由笛卡儿网格构成的近似挖洞面。根据笛卡儿网格与物面的相对位置关系，又将其划分为“外部单元”、“内部单元”和“边缘单元”，边缘单元的集合即是近似挖洞面。在洞映射方法的应用中发现，包围物体所有物面单元建立洞映射模型包含了较多无效的空间位置。以泰坦四号(Titan IV)运载火箭[23]为例，主火箭与助推级轴向长度存在较大差异，助推级网格仅与主火箭中后部区域重叠，因此主火箭头部附近物面所构建的洞映射模型无实际意义。为削减洞映射模型内存消耗量，在模型建立时先判断各物体网格包围盒相交的情况，仅在其他物体网格涵盖的范围内建立洞映射模型。这样，新的洞映射边界就由物面、网格边界和截断面构成，显然这是一个可供其他网格挖洞的最“紧凑”区域，称为“最小洞映射[24]”。泰坦火箭所建立的最小洞映射模型如图1所示，方框为各洞映射模型，其中主火箭洞映射模型较之前有显著减小，网格量削减了75%。

图1 Titan IV运载火箭洞映射模型Fig.1 Hole mapping model of Titan IV launch vehicle

当物面网格发生重叠时，空间网格离散方式发生了一些变化，物体初始体网格也可能是洞内点。以图 2为例，图中机身网格为去掉机翼单独生成，拓扑结构简单，网格质量较好，机翼网格也单独生成，然后将机翼网格嵌套入机身网格中，这样，落在机翼物面内的机身网格实质为洞内点，“Inverse Mark”[24]标识方法不再适用。为此，本文将已建好的洞映射单元标识为临时单元，将有物面网格落入的单元标识为过渡单元；对洞映射模型的8个角单元进行判断，若当前角单元不是过渡单元，则将该单元标识为正常单元；感染所有正常单元的相邻单元，若该单元为临时单元，则将其标识为正常单元，直至再没有临时单元转换为正常单元为止；最后将剩余的临时单元标识为内部单元，进而完成了洞映射模型的标识。

图2 机身网格洞内点Fig.2 Hole points of wing grid

由于洞映射方法的固有特点，对模型表面模拟得越精细，所需的笛卡儿网格量就越大，内存开销就越大。PEGASUS5.2[25]就通过细分洞映射模型，区别各洞映射模型笛卡儿网格尺度，针对精细结构洞映射模型采用较小尺寸的笛卡儿网格，如窄缝等，从而在保证对模型细节精细化描述的前提下尽可能节省网格开销。本文对落入洞映射模型过渡单元的网格点进行一次再判断，在不增加原有笛卡儿网格量的基础上解决物面附近网格点的属性判断问题，本文称之为“复合式挖洞方法”。图 3为复合式挖洞方法示意图，图中黑色方框为洞映射模型，左下角白色单元为内部单元，为洞内区域，灰色单元为过渡单元，右上角为外部单元，网格为该物体体网格。图中包含四种点，落在外部单元的正常点P1，落在内部单元的洞内点P4，还有一种则是落在过渡单元的点，可能是洞内点如P3，也可能是正常点如P2。加密洞映射也能够对P2和P3进行更精确的判断，但增加了网格量。在此，本文通过对落入过渡单元的点进行寻找贡献单元的操作，进而确定该点的属性，具体的实现方法如下。

1) 建立最小洞映射模型，通过上述方法标识笛卡儿网格的外部单元、内部单元和过渡单元。

2) 通过洞映射模型对其他网格进行挖洞，将落入外部单元的点标识为正常点Fix，将落入内部单元的点标识成为受保护洞内点Pthole。

3) 针对有物面网格重叠的物体，进行非重叠的物面网格单元寻点操作，若贡献单元与该网格同属一个物体且贡献单元网格层级较低，则将该贡献单元各顶点标识为受保护洞内点Pthole；再对体网格单元进行寻点操作，若贡献单元与该网格同属一个物体且贡献单元网格层级较低，则将贡献单元的正常点Fix标识为普通洞内点Hole。

4) 针对物面网格重叠的物体体网格，感染受保护洞内点Pthole毗邻的正常点Fix，将其标识为受保护洞内点Pthole，直至再没有正常点Fix发生转化为止。

5) 对落入其他物体洞映射过渡单元的网格点，若能找到有效的贡献单元(存在贡献单元且贡献单元不为受保护洞内点Pthole或者普通洞内点Hole)，则该点为正常点Fix，否则为普通洞内点Hole。

6) 针对拉伸背景网格，进行网格单元寻点操作，若存在贡献单元，则将该网格标识为普通洞内点Hole。

对于有物面网格重叠的情况，需要对同属一个物体的网格进行分层处理，以方便挖洞过程。如翼身组合体，将模型拆成机身部分和机翼部分，两部分单独生成拓扑简单的网格，其中机翼网格为高层网格，机身网格为低层网格。

图3 洞映射与四类点示意图Fig.3 Sketch map of hole-mapping cells and four kinds of nodes

以较为常见的导弹为例，导弹由弹身及气动舵组成，舵与弹身之间一般存在着细微的缝隙，若洞映射单元尺寸过太，缝隙将被边邻单元填补，无法实现挖洞，因此在这种情况下洞映射单元尺寸得小于缝隙。传统洞映射方法与最小洞映射方法生成的导弹洞映射截面如图 4(a)所示，复合式挖洞方法生成的导弹洞映射截面如图 4(b)所示。传统洞映射方法、最小洞映射方法和复合式挖洞方法的洞映射笛卡儿单元以及挖洞时间对比见表1，从表可以看出复合式挖洞方法显著减少了笛卡儿网格数目，同时相对其他两种方法并没有消耗过多时间。

通过复合式挖洞方法可以在不额外增加内存开销的前提下对网格进行挖洞处理，同时保证挖洞效率。

图4 3种挖洞方法洞映射截面对比Fig.4 Comparison of hole-mapping section among three hole-cutting algorithms

表1 3种挖洞方法比较Table 1 Comparison among three hole-cutting algorithms

AlgorithmCartesiangridTimeofhole⁃cutting/sOriginal59790560．4744Minimum18440530．4712Composite1651720．5035

2 基于虚网格的格心ADT搜索方法

寻点是重叠网格的另一项关键技术，是确定网格点在其他网格中的位置、查找网格贡献单元的统称。在整个重叠网格过程中，需要反复寻找插值点的位置及插值点的贡献单元，因此准确性和效率是寻点方法的关键。目前基于格心网格的有限体积法在CFD中应用广泛，而格心网格块与块之间存在间隙，空间上不连续，这就给ADT(Alternating Digital Tree)[26]叉树结构的建立造成了不便。目前一种常用的解决方法是通过虚网格将格心单元进行延拓，填补块与块之间的空白部分，保证空间的连续性。本文先通过线性外插的方式，分别沿i、j、k3个方向对各个块的格心网格进行延拓，再利用对接边界条件，通过查找方块相应点对虚网格坐标进行修正，使得分区边界上的虚网格坐标严格对应于对应块实网格坐标，实现格心虚网格的延拓。通过这种方式，既可以实现内部网格点的准确延拓，又能实现远场、对称面等边界网格的严格对接。

在完成格心单元虚网格延拓之后，首先需要组织ADT叉树，对空间网格单元进行规整。以二维情况为例，图 5中包含了7个网格单元，节点1包含整个区域，为ADT叉树的根节点。在根节点下插入子节点——节点2，由于该节点落在节点1所指代区域的右半区域，因此将节点1所指代的空间二分，节点2指代右半区域。同理，节点3指代左半区域，以此类推，形成了如图 5所示的ADT叉树结构。图中各节点旁的外边框为ADT叉树所包含的整个区域，灰色部分为该节点所指代的区域，如节点3指代左半区域。假设有一待查询点P，如图 5所示。将点P代入ADT叉树中进行搜索，点P落入根节点——节点1所指代的整个区域，因此节点1是备选单元，同理，节点2、5、6所指代的区域同样包含点P，故也是备选单元。然后通过单元的空间包围盒是否相交排除一部分备选单元，剩余的备选单元通过等参变换，计算出点P在该单元的权值，再结合模版漫游(Stencil-walking[27])法，确定最终的贡献单元以及插值系数。

图5 ADT搜索方法Fig.5 ADT searching method

对于有多个物体重叠的情况，应尽可能减小搜索范围，以提高搜索效率。图6为3个物体重叠时搜索空间示意图，图中实线为各物体网格外边界，虚线为包围盒。以Obj3为例，Obj3中处于阴影区域内的网格不与其他物体网格相交，故该区域内网格不会成为其他物体网格的贡献单元，为此在ADT叉树建立时排除该部分网格，以减少ADT叉树中无效结点的数目，本文称之为“有效搜索”。

有效搜索对各物体间网格包围盒相交较少的情况效果显著。以泰坦四号运载火箭为例，主火箭网格为200万，助推火箭网格为30万，网格如图 7所示，其中助推火箭网格仅延伸至主火箭中部，主火箭前部网格以及外部网格对寻点毫无贡献，故通过有效搜索能将其剔除。改进前后ADT节点数目、ADT建立时间以及贡献单元搜索时间如表 2所示，其中ADT节点数目、ADT叉树建立时间及贡献单元搜索时间显著减少。

图6 3个物体重叠时的搜索空间Fig.6 Overlapping search space of three objects

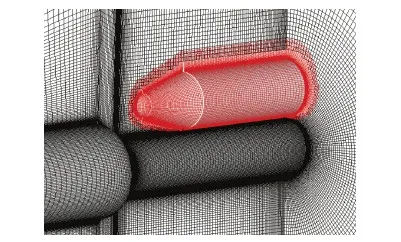
图7 Titan IV运载火箭网格重叠Fig.7 Overlapping grids of Titan IV launch vehicle

表2 原始的和改进的寻点方法比较

Table2Comparisonbetweenoriginalandimproveddonorsearchalgorithms

AlgorithmADTnodeTimeofATDbuilding/sTimeofdonorsearch/sOriginal23929804．37586．1862Improved7023191．10933．3455

3 改进的混合洞面优化方法

洞面优化方法目的是改善重叠区域，将“挖洞”过程后建立的初始插值边界推离物面，从而避免插值点落入边界层内部降低流场求解精度。插值边界的位置以及它与贡献单元的相互匹配关系影响整个流场的计算，因此插值边界的确定是整个洞面优化过程的关键。

文献[28]对典型的洞面优化方法进行了概述，同时通过对割补法的分析，针对其洞面切割后洞边界位置不确定性及不可预知性问题，提出将其与物面距离优化准则相结合的新型混合洞面优化方法。在后续的算例测试中发现，由于填补阶段回填终止判据过于严格，阵面会推进异常。图8 为RAE2822翼型测试算例，网格由三部分组成，翼型前部网格Grid 1、后部网格Grid 2以及拉伸的直角背景网格Grid 3。由于切割后网格缝隙正好也处于虚线框处，填补时该区域洞边界单元较多，早期的判别准则要求贡献单元全部为正常点，而背景网格洞边界插值点的贡献单元大多为洞边界单元，故阵面会持续推进，进而出现图中网格异常现象。而对于窄缝问题，例如机翼挂载分离算例中挂载物与挂架之间的窄缝，填补阶段阵面会推进至洞内点位置，正常点毗邻洞内点造成插值阵面部分缺失从而导致该区域重叠失败。

图8 RAE2822翼型网格重叠图Fig.8 Overlapping grids of RAE2822 airfoil

本文对填补过程判别法则进行修改，将以插值点贡献单元全为正常点的判别条件改为直接设定阵面推进步数，同时引入两类受保护洞内点Ntpthole 1与Ntpthole 2，确保两层插值边界的建立，提高优化过程的鲁棒性。改进型的混合洞面优化方法具体过程如下。

1) 求解各网格点到本物体的物面距离d0，若该网格点隶属于背景网格，则将d0记为一个较大的值，如1×106m。

2) 将所有网格点标记成为正常点Fix。

3) 通过复合式挖洞方法对网格进行挖洞。

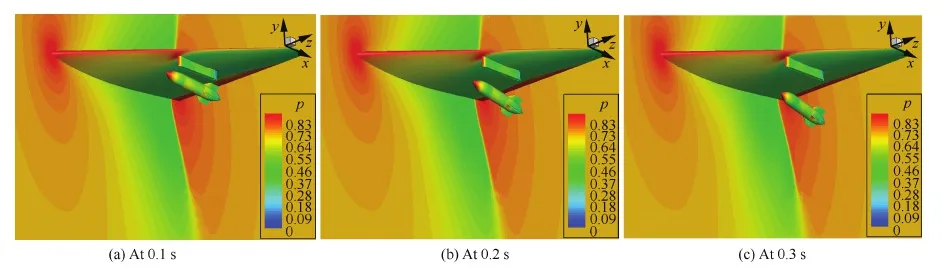
4) 对所有的网格点进行ADT寻点操作，找到其所有贡献单元，且贡献单元不与该点同属于一物体，通过三线性插值方法计算出该点到其他物面的最小距离dmin，若d0

5) 对所有落在远场边界条件上的正常点Fix进行ADT寻点操作，若存在有效贡献单元(贡献单元不为洞内点Pthole或Hole)，将其标识为临界点Crt，将其相邻的非落在远场边界上的正常点Fix标记为洞边界点Frg 1。

6) 将与洞内点Pthole、Hole相邻的正常点Fix标识为洞边界点Frg 1。

7) 对洞边界进行切割操作。针对所有洞边界点Frg 1寻点，若存在有效的贡献单元，则该点标识为普通洞内点Hole，与之相邻的正常点Fix标识为洞边界点Frg 1，直至再没有正常点Fix转化为洞边界点Frg 1为止。

8) 将与受保护洞内点Pthole相邻的非受保护洞内点标识为第1类受保护洞内点Ntpthole 1。

9) 将与第1类受保护洞内点Ntpthole 1相邻的非受保护洞内点且非第1类受保护洞内点标识为第2类受保护洞内点Ntpthole 2。

10) 对洞边界进行回填操作。针对所有洞边界点Frg 1，将该点转化为正常点Fix，将其相邻的普通洞内点Hole转化为洞边界Frg 1。

11) 重复过程10)N次(经验值N=4)。

12) 将毗邻正常点Fix的第2类受保护洞内点Ntpthole 2标记成为洞边界点Frg 1。

13) 将毗邻洞边界点Frg 1的非正常点标识为洞边界点Frg 2。

14) 检索所有的插值点Frg 1和Frg 2，将非正常插值点(不存在贡献单元或贡献单元不全是正常点)用其相邻正常插值点贡献单元代替。

15) 将剩余的两类受保护洞内点Ntpthole 1与Ntpthole 2转化为普通洞内点Hole。

16) 针对相对运动数值模拟，对所有的洞内点Hole、临界点Crt进行寻点，若存在有效贡献单元，则将其标识为插值点Frg 3。

其中，正常点Fix为参与计算的网格点，洞内点(包括受保护洞内点Pthole和普通洞内点Hole)、临界点Crt以及洞边界点Frg 1、Frg 2、Frg 3为不参与流场计算的点，但洞边界点 Frg 1、Frg 2、Frg 3的守恒变量通过向正常点Fix插值获得更新。同时，网格点一旦被标识为受保护洞内点Pthole，其属性在优化的任一环节均不会被修改。洞面优化完成后通过检索普通洞内点Hole、临界点Crt，尽可能多地将其转变为插值点Frg 3，使其在非定常相对运动数值模拟过程中守恒变量与当地值匹配，尽可能减少网格运动至下一个时刻时普通洞内点Hole、临界点Crt直接变成正常点Fix对流场收敛带来的影响。图9为该洞面优化过程，简要示意了该洞面优化的主要过程，图 9(a)为复合式挖洞后的网格示意图，对应洞面优化阶段1)～3)；图9(b)为采用壁面距离准

图9 洞面优化过程示意图Fig.9 Sketch map of hole optimization process

则标记普通洞内点，对应洞面优化阶段4)；图 9(c)为建立第一层插值边界及网格切割，二者对应洞面优化阶段5)～7)；图 9(d)为标记两类受保护洞内点以及网格回填，对应洞面优化阶段8)～12)；图 9(e)为建立其余的插值边界，对应洞面优化阶段13)～16)。图 10为采用改进后的混合洞面优化方法优化后的网格，图 8中网格回填异常情况消失。

图10 RAE2822网格改进型混合洞面优化结果Fig.10 RAE2822 grids optimized result by improved mixed overlapping optimization method

4 物面网格重叠技术

飞行器表面非常复杂，较难生成高质量的多块结构网格，因此希望在物面网格重叠的基础上取消空间网格的拓扑限制，从而降低空间网格生成难度。在重叠网格生成过程中，若对物面网格进行分块后独立生成，则有可能因为各部分的网格几何误差、物面曲率分辨率和光滑程度等因素的不同而导致重叠区内彼此描述的物面不唯一，即“物面失配”问题。图 11为网格物面重叠中比较常见的两种情况。图 11(a)中物面为凹曲面，二者物面网格点均不落入对方网格中，无法完成贡献单元搜索；图 11(b)中物面为凸曲面，尽管二者物面网格均落入对方网格中，但贡献单元远离对方物面，由于边界层内流动梯度大，因此容易产生较大的插值误差进而影响流场的求解。

图11 网格物面与物理物面失配问题Fig.11 Miss match of body and grid surface

本文采用PEGASUS5[7]中的物面投影方法，将物面网格向目标物面投影计算偏移量，再对近物面网格进行坐标修正，使其能找到合理的贡献单元，从而实现物面附近网格间流动变量的正确传递。本文首先对各物体物面建立ADT叉树，通过ADT查找物面网格潜在投影单元，然后再利用Stencil-walking法做进一步的判断。曲面上使用Stencil-walking法的计算公式为

(1)

(2)

式中：ε通常取值0.01；Δs为网格距离；f为修正协调函数，当插值点在物面附近时取1，距离物面较远时取0，实现坐标修正光滑过渡。

5 计算方法

流动控制方程为三维可压缩Navier-Stokes方程。一般曲线坐标系下，无量纲化的方程守恒形式为[29]

(3)

式中：Q为守恒变量；F、G和H为对流通量；Fv、Gv和Hv为黏性通量；t为时间；Re为自由来流雷诺数。

采用有限体积法对控制方程进行离散求解，空间离散采用Roe的FDS(Flux Difference Splitting)格式、MUSCL(Monotone Upstream-centred Schemes for Conservation Laws)插值方法和Van Albada以及minmod限制器用于获得二阶空间离散精度，湍流模型采用S-A(Spalart-Allmaras)模型，时间离散方法为LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法，非定常时间推进采用双时间步方法。

6 算例及计算结果

6.1 翼身组合体DLR-F6

为验证该物面重叠网格修正方法的正确性以及静态复杂算例的模拟能力，本文选取德国宇航公司的DLR-F6翼身组合体(简称DLR-F6 WB[30])跨声速扰流作为验证算例。计算来流马赫数Ma=0.75，雷诺数Re=3×106，升力系数CL=0.500。该计算模型为半模，总共分为粗、中、细以及极细四套网格，网格量分别为300万、500万、750万以及1 000万，图 12为DLR-F6 WB机翼、机身网格重叠示意图。

图13为该工况下DLR-F6 WB模型表面及对称面压力系数Cp分布图，图中机翼与机身网格重叠区域等压力系数线过渡光滑，分布合理，机翼表面激波结构清晰，说明本重叠网格方法在物面附近的处理是正确合理的。图 14为该工况下机翼η=33.1%和η=51.4%站位不同密度的压力系数分布对比。计算结果表明，各种不同密度网格计算得到的压力分布基本相同，均与实验值吻合良好，不同的是激波位置与激波强度。

图 12 DLR-F6 WB网格重叠示意图Fig.12 Sketch map of overlapping grids for DLR-F6 WB

图13 DLR-F6 WB模型对称面及表面压力系数云图Fig.13 Pressure coefficient contours on symmetric plane and surface of DLR-F6 WB model

图 14 DLR-F6 WB机翼表面压力系数分布Fig.14 Surface pressure coefficient distribution for DLR-F6 WB wing

6.2 机翼挂载分离

机翼挂载分离模型是测试非定常多体相对运动数值模拟能力的一个标准算例，可用来验证动网格、六自由度方程模型以及非定常数值算法的正确性和准确性。该模型由3部分组成，机翼、挂架以及外挂物，其几何外形参数及其他参数详见文献[31]。计算条件为：Ma=0.95、H=7.92 km、α=0°，H为飞行高度，α为迎角。其中网格由四部分组成，机翼网格、挂架网格、外挂物网格以及拉伸的直角背景网格，总网格量为565万，其中机翼网格为400万，挂架网格为15万，挂载物网格为50万，背景网格为100万，其网格重叠情况如图15所示。机翼和挂架间物面和近物面网格相互重叠，如图16所示。

图17为分离过程0.1 s、0.2 s和0.3 s表面以及对称面压力分布图，由图可以看出计算得到的激波结构清晰，挂架附近物面处等值线过渡光滑。图 18为挂载物三方向力系数Cx、Cy和Cz、力矩系数Cl、Cm和Cn、角速度ωx、ωy和ωz、角位移、速度u、v和w以及位移的计算值与实验结果对比图，图中CFD代表计算结果，Exp.代表实验结果，二者吻合良好，验证了本文非定常多体相对运动数值模拟的精确性。由于本算例弹射力作用方式与实验有差别，且弹射力量值较大，z方向较小的位移也会造成较大的滚转力矩变化，从而出现图18(c)中滚转通道角速率与实验值有一定偏差的现象，这在文献[32]中也有相应的论述。

图15 机翼/挂架/挂载物网格示意图Fig.15 Sketch map of grids of wing/pylon/store

图16 机翼/挂架网格重叠示意图Fig.16 Sketch map of overlapping grids of wing and pylon

图17 各时刻表面及对称面压力分布Fig.17 Surface and symmetric plane pressure contours at each moment

图18 计算结果与实验结果对比Fig.18 Comparison of calculation and experiment results

7 结 论

为降低CFD计算过程中网格生成难度，本文基于结构重叠网格技术，提出了新的挖洞、寻点和洞面优化方法，并实现了带有物面网格重叠的静态定常、动态非定常数值模拟，重叠过程无需人工干预，自动化程度和鲁棒性高。

1) 在最小洞映射的基础上修改洞映射模型标识方法，确保洞映射模型准确标识，通过对落入洞映射模型过渡单元的点进行再判断，提出复合式挖洞方法，在不增加额外内存消耗的前提下准确标识网格点属性，实现网格挖洞过程。

2) 通过对格心坐标虚网格进行延拓，确保格心系统空间的连续性，实现格心系统下寻点，提出有效搜索思想，提高了寻点效率。

3) 改变混合洞面优化方法填补阶段判别法则，引入两类受保护洞内点，确保存在窄缝等严苛条件下两层插值边界的建立，同时将合适的洞内点Hole、临界点Crt转换为插值点Frg 3，以利于非定常多体相对运动数值模拟过程收敛。

4) 利用物面投影法对物面网格重叠中的近壁面网格坐标进行修正，使其能准确找到贡献单元，实现了物面附近流动变量的正确传递。

[1] THOMAS H P, ANTHONY J S. High-lift OVERFLOW analysis of the DLR-F11 wind tunnel model： AIAA-2014-2697[R]. Reston: AIAA, 2014.

[2] MENDENHALL M R, LESIEUTRE D J, CARUSO S C, et al. Aerodynamic design of pegasustm, concept to flight with CFD： AGARD CP 43[R]. Paris: AGARD, 1980.

[3] LIEVER P A, HABCHI S D. Separation analysis of launch vehicle crew escape systems: AIAA-2004-4726[R]. Reston: AIAA, 2004.

[4] WOODEN P A, BRYAN W, JUBARAJ S B. Calibrating CFD predictions for use in multiple store separation analysis: AIAA-1998-0754[R]. Reston: AIAA, 1998.

[5] KIM J W, PARK S H, YU Y H. Euler and Navier-Stokes simulations of helicopter rotor blade in forward flight using an overlapped grid solver: AIAA-2009-4268[R]. Reston: AIAA, 2009.

[6] BENEK J A, STEGER J L, DOUGHERTY F C. A flexible grid embedding technique with applications to the Euler equations: AIAA-1983-1944[R]. Reston: AIAA, 1983.

[7] ROGERS S E, SUHS N E, DIETZ W E. PEGASUS 5: An automated preprocessor for overset-grid computational fluid dynamics[J]. AIAA Journal, 2003, 41(6): 1037-1045.

[8] WILLIAM M C. The overgrid interface for computational simulations on overset grids: AIAA-2002-3188[R]. Reston: AIAA, 2002.

[9] NOACK R W. SUGGAR: A general capability for moving body overset grid assembly: AIAA-2005-5117[R]. Reston: AIAA, 2005.

[10] CHEN S Y, CHEN Y C, XIA Z H, et al. Constrained large-eddy simulation and detached eddy simulation of flow past a commercial aircraft at 14 degrees angle of attack[J]. Sci China-Phys Mech Astron, 2013, 56(2): 270-276.

[11] ZHAO M, CAO Y H. Numerical simulation of rotor flow field based on overset grids and several spatial and temporal discretization schemes[J]. Chinese Journal of Aeronautics, 2012, 25(2):155-163.

[12] 徐嘉, 刘秋洪, 蔡晋生, 等. 基于隐式嵌套重叠网格技术的阻力预测[J]. 航空学报, 2013, 34(2): 208-217.

XU J, LIU Q H,CAI J S, et al. Drag prediction based on overset grids with implicit hole cutting technique[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 208-217 (in Chinese).

[13] 田书玲, 伍贻兆, 夏健. 基于非结构重叠网格的二维外挂物投放模拟[J]. 空气动力学学报, 2007, 25(2): 225-249.

TIAN S L, WU Y Z, XIA J. 2D store separation simulation using unstructured overlapping grid[J]. Acta Aerodynamica Sinica, 2007, 25(2):225-249 (in Chinese).

[14] 田书玲, 伍贻兆, 夏健. 基于动态非结构重叠网格法的直升机前飞非定常流场数值模拟研究[J]. 航空学报, 2007, 28(5): 1047-1054.

TIAN S L, WU Y Z, XIA J. Numerical simulation research of unsteady flow field around helicopter in forward flight on dynamic overset unstructured grids[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(5):1047-1054 (in Chinese).

[15] 田书玲, 伍贻兆, 夏健. 用动态非结构重叠网格法模拟三维多体相对运动绕流[J]. 航空学报, 2007, 28(1): 46-51.

TIAN S L, WU Y Z, XIA J. Simulation of flow past multri-body in relative motion with dynamic unstructured overset grid method[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 46-51 (in Chinese).

[16] SLOTNICK J, KANDULA M, BUNING P. Navier-Stokes simulation of the space shuttle launch vehicle flight transonic flowfield using a large scale Chimera grid system: AIAA-1994-1860[R]. Reston: AIAA, 1994.

[17] LABOZZETTA W F, GATZKE T D. MACGS-towards the complete grid generation system: AIAA-1994-1923[R]. Reston: AIAA, 1994.

[18] CHIU I, MEAKIN R. On automating domain connectivity for overset grids: AIAA-1995-0854[R]. Reston: AIAA, 1995.

[19] MEAKIN R. Object x-ray for cutting holes in composite overset structured grids: AIAA-2001-2537[R]. Reston: AIAA, 2001.

[20] NOACK R W. Resolution appropriate overset grid assembly for structured and unstructured grids: AIAA-2003-4123[R]. Reston: AIAA, 2003.

[21] NOACK R W. A direct cut approach for overset hole cutting: AIAA-2007-3835[R]. Reston: AIAA, 2007.

[22] LEE Y L, BAEDER J D. Implicit hole cutting-a new approach to overset grid connectivity: AIAA-2003-4128[R]. Reston: AIAA, 2003.

[23] TAYLOR S, WANG J C T. Launch-vehicle simulations using a concurrent, implicit Navier-Stokes solver: AIAA-1995-0223[R]. Reston: AIAA, 1995.

[24] 袁武, 阎超, 席柯. 洞映射方法的研究和改进[J]. 北京航空航天大学学报, 2012, 38(4): 563-568.

YUAN W, YAN C, XI K. Investigation and enhancement of hole mapping method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 563-568 (in Chinese).

[25] STUART E R. Improvements to the Pegasus5 overset CFD software[C]//12th Symposium on Overset Grids and Solution Technology, 2014.

[26] BONET J, PERAIRE J. An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems[J]. International Journal for Numerical Methods in Engineering, 1991, 31(1): 1-17.

[27] BELK D M, MAPLE R C. Automated assembly of structured grids for moving body problems: AIAA-1995-1680[R]. Reston: AIAA, 1995.

[28] 王文, 阎超, 袁武, 等. 新型重叠网格洞面优化方法及其应用[J]. 航空学报, 2016, 37(3): 826-835.

WANG W, YAN C, YUAN W, et al. Novel overlapping optimization algorithm and its applications[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 826-835 (in Chinese).

[29] 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 18-25.

YAN C. Computational fluid dynamic’s methods and applications[M]. Beijing: Beihang University Press, 2006: 18-25 (in Chinese).

[30] KELLY R, BRODERSEN O. Summary of data from the second AIAA CFD drag prediction workshop: AIAA-2004-0555[R]. Reston: AIAA, 2004.

[31] HALL L H, PARTHASARATHY V. Validation of an automated chimera/6-DOF methodology for multiple moving body problems: AIAA-1998-0767[R]. Reston: AIAA, 1998.

[32] LEE S, PARK M, CHO K W, et al. A new automated chimera method for the prediction of store trajectory: AIAA-1999-3131[R]. Reston: AIAA, 1999.

王文男， 博士研究生。主要研究方向： 计算流体力学， 重叠网格方法。

Tel: 010-82338071

E-mail: wangwenbuaa@126.com

阎超男， 博士， 教授， 博士生导师。主要研究方向： 空气动力学， 计算流体力学。

Tel: 010-82317019

E-mail: yanchao@buaa.edu.cn

URL：www.cnki.net/kcms/detail/11.1929.V.20160222.1027.004.html

Arobustandautomaticstructuredoverlappinggridapproach

WANGWen1,YANChao1,*,YUANWu2,HUANGYu1,XIKe3

1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China2.SupercomputingCenter,ComputerNetworkInformationCenter,ChineseAcademyofSciences,Beijing100190,China3.InstituteofOrdnanceIndustryNavigationandControlTechnology,Beijing100089,China

Thegridtechnologyisacrucialaspectofnumericalsimulationuptillthepresentmoment.Overlappinggridtechnologycouldrelaxtherestrictionofstructuretopology,thusreducingthedifficultyofgridgeneration.Basedonthestructuredoverlappinggrid,hole-cutting,donorsearch,andoverlappingoptimizationareexploredandimproved,andsurfacegridassemblageiscompletedinthisthesis.Simultaneously,arobustandautomaticgridoverlappingsystemisconstructed.Inordertosavememory,basedontheminimumholemappingmethod,acompositehole-cuttingmethodisproposed.Regardingdonorsearch,thecontinuityofthesearchspaceispreservedwiththevirtualcell-centeredgrid.Moreover,thenodesofalternatingdigitaltree(ADT)aredecreasedbyanefficientsearchalgorithmwhichexcludessomenon-contributinggridpoints.Withrespecttooverlappingoptimization,twokindsofprotectedhole-pointsareinsertedandanewprincipleisdevelopedtoensuretheconstructionoftwointerpolatedlayersinpastephase,intensifyingtherobustnessofoverlappingoptimization.Thecoordinatesofnear-bodygridsarecorrectedbyprojectionmethodtomakesuretheaccuratetransmissionofflowvariables.Withtheenhancedalgorithm,asteadyDLR-F6wing-bodyflowandanunsteadywing/pylon/storeseparationflowareperformed,andexcellentagreementofcomputationalresultscomparedwithexperimentaldatahasbeenachieved.Thealgorithmshowsremarkablecapabilityandaccuracyinthesimulationofsteadyorunsteadymultiplebodiesflowandprovidesgreatapplicationvalueforengineering.

computationalfluiddynamics;structuredoverlappinggrid;hole-mapping;donorsearch;holeoptimizationmethod;wing-body;wing/pylon/storeseparation

2016-01-03；Revised2016-01-18；Accepted2016-01-29；Publishedonline2016-02-221027

.Tel.：010-82317019E-mailyanchao@buaa.edu.cn

2016-01-03；退修日期2016-01-18；录用日期2016-01-29； < class="emphasis_bold">网络出版时间

时间：2016-02-221027

www.cnki.net/kcms/detail/11.1929.V.20160222.1027.004.html

.Tel.：010-82317019E-mailyanchao@buaa.edu.cn

王文， 阎超， 袁武， 等． 鲁棒的结构网格自动化重叠方法J． 航空学报,2016,37(10):2980-2991.WANGW,YANC,YUANW,etal.ArobustandautomaticstructuredoverlappinggridapproachJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):2980-2991.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0034

V211.3

A

1000-6893(2016)10-2980-12