第12讲“贵了探索型问题”复习精讲

韩芬

专题精讲

规律探索型问题也是归纳猜想型问题，其特点是：给出一组具有某种特定关系的数、式、图形，或给出与图形有关的操作变化过程，或某一具体的问题情境，要求通过观察分析推理，探究其中蕴涵的规律，进而归纳或猜想出一般性的结论，主要有“数列规律”“计算规律”“图形规律”与“动态规律”等题型，

规律探索问题的解题方法一般是通过观察、类比特殊情况（特殊点、特殊数量、特殊线段、特殊位置等）中的数据特点，将数据进行分解重组、猜想、归纳得出规律，并用数学语言来表达这种规律，同时要用结论去检验特殊情况，以肯定结论的正确性，

点拨：对于数字规律问题主要是在分析比较的基础上发现题目中所蕴涵的数量关系，先猜想，然后通过适当的计算回答问题，此题主要考查探寻数字规律问题，注意观察总结规律，并能正确应用规律，解答此题的关键是判断出：1+3+5+…+（2n-1）=n²，

点拨：对于数式规律问题主要是通过观察、分析、归纳、验证，然后得出一般性的结论，以列代数式即函数关系式为主要内容，此题考查数式的规律，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题，

三.图形规律型

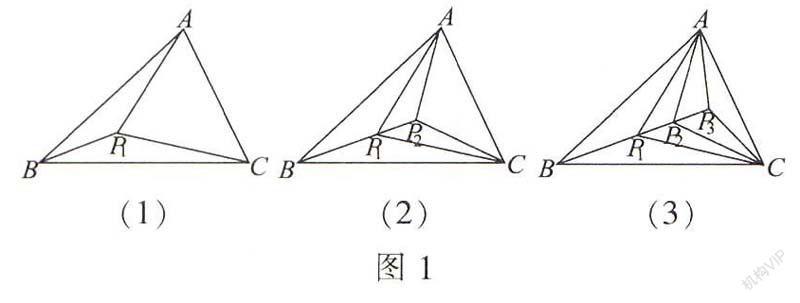
例3（2015·聊城）如图1（1），△ABC的三个顶点和它内部的点Pl，把△ABC分成3个互不重叠的小三角形；如图l（2），AABC的三个顶点和它内部的点Pl、P2，把△ABC分成5个互不重叠的小三角形；如图1（3），△ABC的三个顶点和它内部的点P1、P2、B，把△ABC分成7个互不重叠的小三角形：…△ABC的三个顶点和它内部的点P1、P2、P3、…、Pn，把△ABC分成个互不重叠的小三角形，

点拨：图形规律问题主要是观察图形的组成、分拆等过程中的特点，分析其联系和区别，用相应的算式描述其中的规律，要注意对应思想和数形结合，本题考查图形的变化规律类型，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，然后通过分析找到各部分的变化规律，直接利用规律求解，

点拨：对于数形结合猜想型问题首先要观察图形，从中发现图形的变化方式，再将图形的变化以数或式的形式反映出来，从而得出图形与数或式的对应关系，数形结合总结出图形的变化规律，进而解决相关问题，此题主要考查了坐标与图形变化问题，解答此题的关键是判断出An的横坐标、纵坐标各是多少，

中考命题预测

1.请观察下面几组数：

1，3，5，7，9，11，13，15……2，5，8，1l，14，17，20，23……7，13，19，25，31，37，43，49……

这三组数具有共同的特点，现在有上述特点的一组数，第一个数是3，第三个数是ll，则其第n个数为（

），

A.8n-5

B.n²+2

C.4n-1

D.2n²-4n+5

2.古希腊数学家把数1，3，6，10，15，21，…叫作三角形数，其中l是第一个三角形数，3是第2个三角形数，6是第3个三角形数……依此类推，那么第9个三角形数是____，2 016是第____个三角形数，