第8讲“动手操作问题”精讲

汪国刚

专题精讲

动手操作问题是指通过动手操作对某种现象获得感性认识，再利用数学知识进行思考、探索和解决的一类问题，这类问题通常以折叠、剪拼、操作探究等形式出现，具有较强的实践性，能够有效考查同学们的实践能力、创新能力和直觉思维能力、发散思维能力等综合素质。

解答动手操作问题的关键是要学会自觉地运用数学知识去观察、分析、抽象、概括所给的实际问题，揭示其数学本质，并转化为我们所熟悉的数学问题，解答实践操作题的基本步骤为：从实例或实物出发，通过具体操作实验，发现其中可能存在的规律，提出问题，检验猜想，在解答过程中一般需要经历操作、观察、思考、想象、推理、探索、发现、总结、归纳等实践活动过程，利用自己已有的生活经验和数学知识去感知发生的现象，从而发现所得到的结论。进而解决问题，

点拨：对于几何问题中求线段之和最小值，通常只有两种模型，即“将军饮马”和“两点之间线段最短”，当两点在直线同侧时，运用前者；当两点分别在直线异侧时，运用后者，通常情况下，求三角形的周长最小值以及求四边形的周长最小值往往也是转化为上述两种模型。

折叠是图形操作问题中的重头戏，其本质就是轴对称，在解决折叠问题时，要注意折叠前后的不变量，包括边与边的关系、角与角的关系等，掌握折叠性质是解题的突破口，找出折叠前后图形中的不变量及全等图形是解决问题的关键，

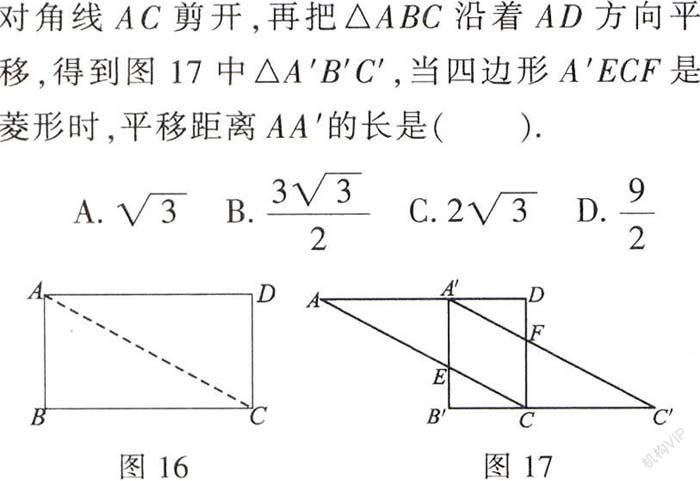
点拨：本题是一道剪拼操作问题，解题过程中运用到平行四边形性质、平移性质、矩形和菱形的判定，

剪与拼是最基本的操作问题，在数学方面就是将图形分割然后重新组合，解决这类问题的关键是能够根据题意画出图形，注意运用转化和分类讨论思想，避免漏解，

点拨：本题考查了旋转的性质，同时也考查了相似三角形的性质与判定，学具操作问题就是用三角板、量角器等学习工具进行摆放，或按设定规则进行图形变换等操作方式所形成的简单数学问题，这种试题在操作问题中较为典型，是中考热点问题，解题时要充分利用图形特有的性质，仔细观察图形变化过程，从而为问题的解决找到突破口。

（2）猜想证明：在图7的情况下，把直线L向上平移到如图8的位置，试问：（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由，

点拨：第（1）题是几何变换综合题，考查分析推理能力、分类讨论思想、数形结合思想，从图象中获取信息，并能利用获取的信息解答相应的问题的能力；第（2）题考查了直角三角形的性质和应用。

操作探究问题是指通过动手测量、作图、取值、计算等操作，猜想获得数学结论的探索研究性活动，实现对题意的理解，解决这类问题需要通过观察、操作、对比、猜想、分析、综合、抽象和概括等实践活动和思维过程，从特殊到一般去研究，有时还要用已学知识加以论证探究所得结论。

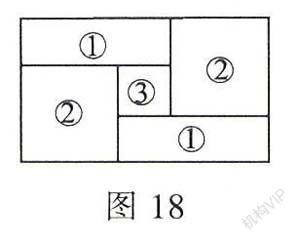
5.如图18，小明家的住房平面图呈长方形。被分割成3个正方形和2个长方形后仍是中心对称图形，若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形标号为（

），

A.①②

B.②③

c.①③

D.①②③

6.[问题提出]用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？

[问题探究]不妨假设能搭成m种不同的等腰三角形，为探究m与n之间的关系，我们可以先从特殊人手，通过试验、观察、类比、最后归纳、猜测得出结论，

[探究一]

（1）用3根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？

此时，显然能搭成一种等腰三角形，所以，当n=3时，m=1，

（2）用4根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？

只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形，所以，当n=4时，m=0

（3）用5根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？

若分成1根木棒、1根木棒和3根木棒。则不能搭成三角形；若分成2根木棒、2根木棒和1根木棒。则能搭成一种等腰三角形，所以，当n=5时，m=1，

（4）用6根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？

若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形；若分成2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形，所以，当n=6时，m=1，

[探究二]

（1）用7根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？（仿照上述探究方法，写出解答过程，并将结果填在表2中）

（2）用8根、9根、10根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？（只需把结果填在表2中）

你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，

[问题解决]用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（设n分别等于4k-1，4K，4k+l，4k+2，其中K是正整数，把结果填在表3中）

[问题应用]用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形（写出解答过程）？其中面积最大的等腰三角形每腰用了根木棒。（只填结果）