归纳猜想的根本:从特殊到一般寻找规律
刘园园
归纳猜想的根本:从特殊到一般寻找规律
刘园园
归纳、猜想、推理在初中数学学习中有着举足轻重的作用,因此在中考中频频出现此类考题.归纳、猜想、推理是由特殊到一般的过程,因此解决此类题目应细心观察分析特殊情况下的结论,进而寻找一般规律.
例1(2014·淮安)如图1,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1四边的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,……,按此方法得到的四边形A8B8C8D8的周长为_______.

图1
【思路突破】顺次连接正方形ABCD四边中点得正方形A1B1C1D1,正方形A1B1C1D1的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形A8B8C8D8的周长,进而根据由特殊到一般的归纳方法,还可寻找到第n个正方形周长的一般结论.
解:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则正方形A1B1C1D1的面积为正方形ABCD面积的一半,则A1B1C1D1周长是ABCD周长的倍;顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,为正方形ABCD的则A2B2C2D2的周长是ABCD的同理,正方形A3B3C3D3的周长是正方形ABCD周长的故第n个正方形周长是原来的
∵正方形ABCD的边长为1,
∴正方形ABCD周长为4,
∴按此方法得到的四边形A8B8C8D8的周长为
例2(2015·常州)数学家哥德巴赫通过研究下面一系列等式,做出了一个著名的猜想.
4=2+2;12=5+7;
6=3+3;14=3+11=7+7;
8=3+5;16=3+13=5+11;
10=3+7=5+5;18=5+13=7+11;
…
通过这组等式,你发现的规律是______ ___________.(请用文字语言表达)
【思路突破】从题目中不难发现等式的左侧是从4开始的连续偶数,即大于2的偶数,右侧则是两数和的形式,关键是寻找两数有何特点或者联系,从而得到答案.
解:通过这组等式,发现的规律是:所有大于2的偶数都可以写成两个质数的和.
【解后反思】寻找规律或总结规律的试题,要注意观察相邻两项之间的变化:差值变化,形状变化,大小变化等,再结合项数进行比较,总结出相应的表达式,即要充分理解运用归纳思想的根本——由特殊情况的区别与联系到一般结论的得出.
例3(2015·安徽)按一定规律排列的一列数:21,22,23,25,28,213,…,若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是_______.
【思路突破】首先判断出这列数中,2的指数各项依次为1,2,3,5,8,13,…,从第三个数起,每个数都是前两数之和.然后根据同底数的幂相乘,底数不变,指数相加,可得这列数中的连续三个数,满足xy=z,据此解答即可.
解:∵21×22=23,22×23=25,23×25=28,25×28= 213,…,
∴x、y、z满足的关系式是:xy=z.
【解后反思】此题主要运用归纳思想探寻数列规律问题,考查了同底数幂的乘法法则,要注意观察并总结规律,还要能正确应用规律.解答此题的关键是先判断出x、y、z的指数特征再探寻一般规律.
例4(2014·盐城)如图2,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图像上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为_____.(用含n的代数式表示,n为正整数)
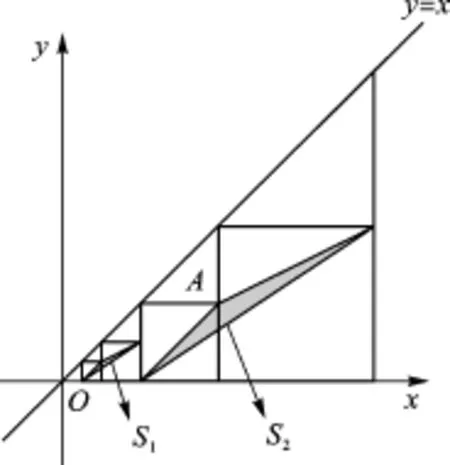
图2
【思路突破】根据函数解析式判断出直线与x轴的夹角为45°,从而得到直线与正方形的边围成的三角形是等腰直角三角形,再根据点A的坐标求出正方形的边长并得到变化规律,从而表示出第n个正方形的边长,然后根据阴影部分的面积等于一个等腰直角三角形的面积加上梯形的面积再减去一个直角三角形的面积,列等式求解并根据结果的规律解答即可.
解:∵函数y=x与x轴的夹角为45°,
∴直线y=x与正方形的边围成的三角形是等腰直角三角形,
∵A(8,4),
∴第四个正方形的边长为8=23,第三个正方形的边长为4=22,第二个正方形的边长为2=21,第一个正方形的边长为1=20,第n个正方形的边长为2n-1,由图可知,

Sn为第(2n-1)个正方形面积的一半,而第(2n-1)个正方形的边长为22n-2,

【解后反思】本题考查了正方形的性质,三角形的面积,一次函数图像上点的坐标特征,依次求出各正方形的边长是解题的关键,难点在于求出阴影Sn所在的正方形和正方形的边长.
归纳猜想型问题在中考中越来越被命题者所注重,这类题要求根据题目中的图形或者数字,分析归纳,直观地发现共同特征或发展变化的趋势,据此去估计规律或者其他相关结论,使带有猜想性质的推断尽可能与现实情况相对应.
(作者单位:江苏省丰县初级中学)

