中考数学中的“归纳猜想”
史新景
中考数学中的“归纳猜想”
史新景

归纳猜想型问题主要分为数字归纳猜想和图形归纳猜想两类,要求同学们在观察、实验、归纳、类比等基础上大胆猜想,得出结论,并能对自己的猜想加以验证.同学们解题时要善于从所提供的数字或图形信息中,寻找共同之处,这个存在于个例中的共性,就是规律.其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论.由于归纳猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,这类问题不但能培养同学们分析、归纳、解决问题的能力,也有利于培养同学们思维的深刻性和创造性,是目前中考的一大热点,此类题目一般难度不大,题型以选择题和填空题为主,分值在5分左右.
例1(2015·淮安)将连续正整数按如下规律排列:
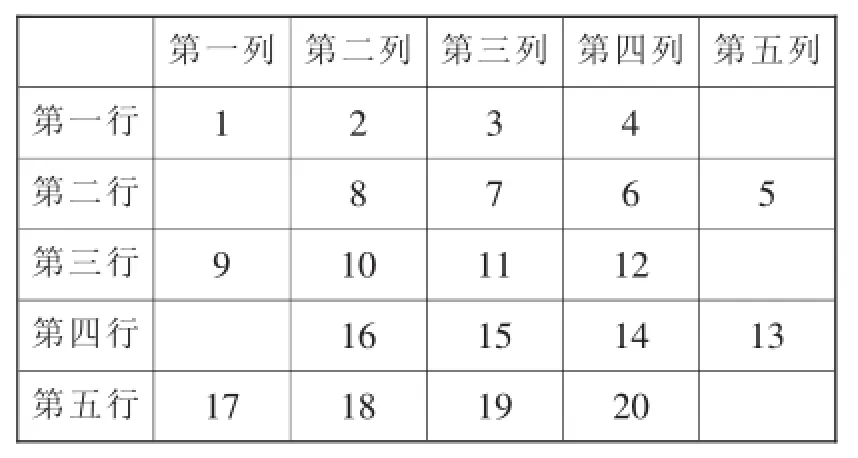
若正整数565位于第a行,第b列,则a+ b=______.
【分析】根据题意可知每行都有4个数,所以用565除以4,根据商和余数的情况判断出正整数565位于第几行;然后根据奇数行的数字在前四列,数字逐渐增加;偶数行的数字在后四列,数字逐渐减小,判断出565在第几列.
【解答】∵565÷4=141…1,
∴正整数565位于第142行,即a=142.
∵奇数行的数字在前四列,数字逐渐增加;偶数行的数字在后四列,数字逐渐减小,
∴正整数565位于第五列,即b=5,
∴a+b=142+5=147.
【点评】此题主要考查了探索数列规律问题,注意观察总结出规律,并能正确地应用规律,
例2(2015·徐州)如图1,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为_______.
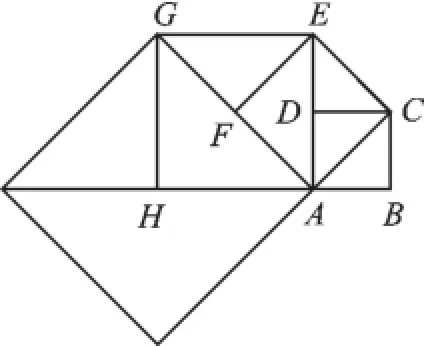
图1
【分析】首先求出AC、AE、AG的长度,然后猜测命题中的数学规律,即可解决问题.
【解答】根据正方形的性质,知:
【点评】此题主要考查探索图形变化规律的问题,需要结合正方形的性质、勾股定理及其应用,归纳得出正方形边长的变化规律.
例3(2015·盐城)设△ABC的面积为1,如图2(1)将边BC、AC分别2等分,BE1、AD1交于点O,△AOB的面积记为S1;如图2(2)将边BC、AC分别3等分,BE1、AD1相交于点O,△AOB的面积记为S2;……;依此类推,则Sn可表示为______.(用含n的代数式表示,其中n为正整数)
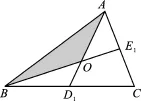
图2 (1)
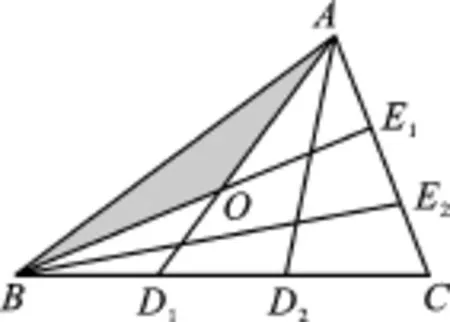
图2 (2)
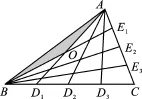
图2 (3)
【分析】连接D1E1,因为△ABO与△OD1E1相似,得从而得到
△OAB的面积为△BE1A面积的又因为△BE1A的面积是△ABC面积的一半,所以△ABO的面积与△ABC的面积比为1∶3,以此类推可以得到答案.
【解答】如图3,连接D1E1,可知D1E1∥AB,得△ABO∽△D1E1O,
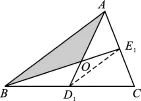
图3
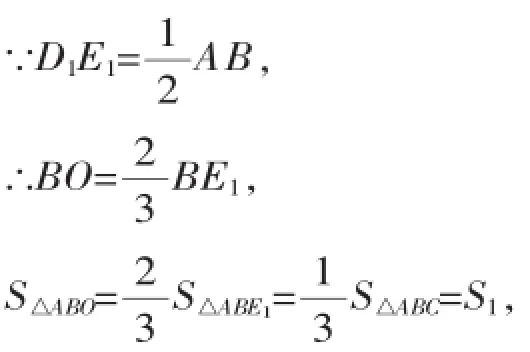

依此类推,Sn可表示为
【点评】此题考查的知识点是相似三角形的判定与性质、平行线分线段成比例定理、三角形的面积,解题关键是根据题意作出辅助线,得出相似三角形.
例4(2015·衢州)已知,正六边形ABCDEF在直角坐标系的位置如图4所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是______.
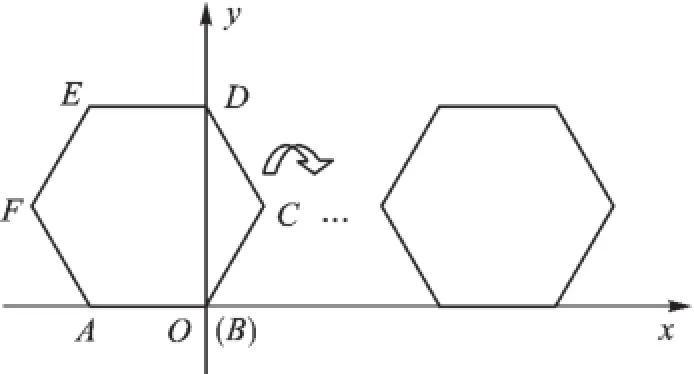
图4
【分析】每6次翻转为一个循环组循环,用2015除以6,根据商和余数的情况确定点B的位置,然后求出翻转前进的距离,过点B作BG⊥x轴于G,求出∠BAG=60°,然后求出AG、BG,再求出OG,最后写出点B的坐标即可.
【解答】因为正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,所以每6次翻转为一个循环组循环,因为2015÷6=335余5,所以经过2015次翻转为第336循环组的第5次翻转,点B处于在开始时点C的位置,如图5.因为A(-2,0),所以AB=2,所以翻转前进的距离为2×2015= 4030.过点B作BG⊥x轴于G,则∠BAG=60°,所以所以OG=4030+1=4031,所以点B的坐标为故答案为
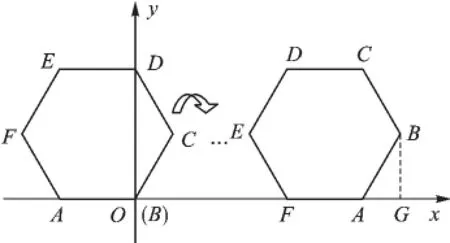
图5
【点评】本题考查了坐标与图形变化,正六边形的性质,确定出最后点B所在的位置是解题的关键,难点在于作辅助线构造出直角三角形.
(作者单位:江苏省丰县初级中学)


