授人以鱼，不如授人以渔——中考数学阅读理解题求解策略

杜茂鼎

授人以鱼，不如授人以渔——中考数学阅读理解题求解策略

杜茂鼎

近年来中考题型的呈现形式越来越多样化，阅读理解题就是最大的一个亮点.阅读理解题往往是先给一个材料，或介绍一个超纲的知识，或给出针对某一种题目的解法，然后再给条件出题.对于这种题，如果为求快速而完全无视阅读材料直接去做题，会浪费大量时间却难有思路，得不偿失.本文针对此内容结合近几年中考题阐述求解策略.

一、阅读理解题的求解技巧

阅读理解题大致可分四类：纯文型（全部用文字展示条件和问题）、图文型（用文字和图形结合展示条件和问题）、表文型（用文字和表格结合展示条件和问题）、改错型（条件、问题、解题过程都已展示，但解题过程要改正）.无论哪种类型，其解题步骤一般都可分为以下几步：

1.快速阅读，把握大意

在阅读时不仅要特别留心短文中的事件情景、具体数据、关键语句等细节，还要注意问题的提出方式.据此估计是我们平常练习时的哪种类型，会涉及哪些知识，一般是如何解决的，在头脑中建立初步印象.

2.仔细阅读，提炼信息

在阅读过程中不仅要注意各个关键数据，还要注意各数据间的内在联系、标明单位，特别是一些特殊条件（如附加公式），以简明的方式列出各量的关系，提炼信息，读“薄”题目.

3.总结信息，建立数模

根据前面提炼的信息分析，通过文中、句的提示作用，选用恰当的数学模型，例如由“大于”“超过”“不足”等联想到建立不等式，由“恰好”“等于”联想到建立方程，由“求哪种方案更经济”联想到运用分类讨论方法解决问题，由“求出……和……的函数关系式”“求最大值（最小值）”联想到建立函数关系，将题中的各种已知量用数学符号相连结，以准确地反映其内在联系.

4.解决数模，回顾检查

在建立好数学模型后，不要急于解决问题，而应回过头来重新审题，一是看哪些数据、关系还没有用上，用得是否准确，要充分挖掘题中的条件并发挥它们的作用；二是关键词句的理解是否准确、到位；三是判断所列关系式是否符合生活经验；四是在解题过程中要善于反思，发现问题及时纠正.

二、阅读理解题的求解展示

1.阅读特殊范例，推出一般结论

例1（2015·铜仁）定义一种新运算：

【思路分析】本题先根据新定义计算出4×2=2，然后再根据新定义计算2×（-1）即可.

2.阅读方法，迁移运用

探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究.

第1次分割，把正方形的面积二等分，

第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为

第3次分割，把上次分割图中空白部分的面积继续二等分，……；

第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为最后空白部分的面积是

第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为

第3次分割，把上次分割图中空白部分的面积继续三等分，……；

第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为最后空白部分的面积是

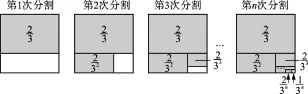
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）

根据第n次分割图可得等式：________，

【思路分析】探究三：根据探究二的分割方法依次进行分割，然后表示出阴影部分的面积，再除以3即可；

解决问题：按照探究二的分割方法依次分割，然后表示出阴影部分的面积，再除以（m-1）即可得解；

拓广应用：先把每一个分数分成1减去一个分数的形式，然后应用公式进行计算即可得解.

【解析】探究三：第1次分割，把正方形的面积四等分，其中阴影部分的面积为

第2次分割，把上次分割图中空白部分的面积继续四等分，阴影部分的面积之和为

第3次分割，把上次分割图中空白部分的面积继续四等分，……；

第n次分割，把上次分割图中空白部分的面积最后四等分，所有阴影部分的面积之和为：

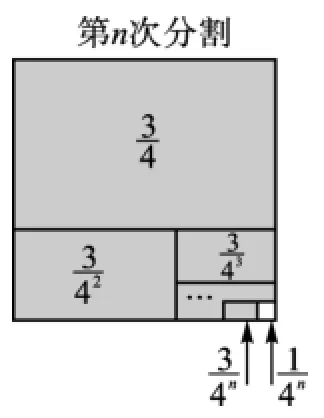
根据第n次分割图可得等式：

两边同除以3，得：

3.阅读范例，运用方法

例3（2015·兰州）为求1+2+22+23+…+2100的值，可令S=1+2+22+23+…+2100，2S=2+ 22+23+24+…+2101，因此2S-S=2101-1，所以S= 2101-1，即1+2+22+23+…+2100=2101-1，仿照以上推理计算1+3+32+33+…+32015的值是_______.

【思路分析】本题从特例入手，通过自学例题解法，探索发现新的解题思路技巧，并用此思路技巧解决新问题.

【解析】我们可先根据等式的性质，得到和的3倍，将两式相减，可得和的2倍，再根据等式的性质，两边都除以2，得到答案.具体解题过程如下：

设M=1+3+32+33+…+32015，①

①式两边都乘3，得

3M=3+32+33+…+32015+32016，②

②-①，得2M=32016-1，

（作者单位：江苏省丰县初级中学）