促进理性思维培养学习习惯——对学生应试反思教学的实践

☉浙江省上虞中学　胡军波

促进理性思维培养学习习惯——对学生应试反思教学的实践

☉浙江省上虞中学胡军波

众所周知，数学学习是否扎实最终需要通过应试来反映，当下数学教学对于应试后学生出现问题的分析往往仅停留在解法之上.我们不乏见到这样的试卷讲评课，教师将试卷中典型错误问题一道一道按此进行分析、点评，并对很多问题给出了较为优秀的解决方法，然后请学生再订正试卷.笔者以为，采用这样陈旧方式进行的“教师讲、学生练”，能在短时期内加深学生对于方法的记忆，但是对于学生自身而言为何犯错？如何提高思维的活跃性？如何培养学习习惯却没有好处.

从应试角度如何提高学生的理性思维？如何培养学生的学习习惯？笔者认为需要从我们的应试反思教学出发，教师首先要改变应试后分析问题、解决问题的习惯，要从只讲解题方法这种单一的方式转变为既分析学生错因、又讲解合理的解决方法，还要从更高的层面上去认知为什么要这样去解决问题，进而提高对于问题的思维方式，从而培养学习习惯.

恩格斯说过：学习要学会反思，要学会分析自己的不足，从不足中得到的进步远大于书本得到的新知.这句话充分阐释了反思对于学习的重要性.笔者以为：应试后，学生应该首先分析自己的得与失，相比以往进步在何处？不足又暴露了哪些？结合暴露的问题，继续思考进一步要去解决的问题.

一、分析取得的进步

从应试中，笔者发现学生对于课堂板演的问题记忆相对深刻，类似演练过的问题相对熟练，可见对于类似问题的解决取得了一定的效果，这是当下数学教学需要完成的首要步骤——模仿.笔者咨询应试后学生的反馈，50%的学生认为自己在模仿环节处理得非常不错，35%的学生认为还可以，只有15%左右的学生认为这里需要加强.笔者对于应试后学生的试卷问题采用了对比式的问题分析，进而提示课堂教学效率的重要性.

问题1设二次函数f（x）=ax2+bx+c，集合A=｛x|f（x）= x｝，且f（x）在区间［-2，2］上的最大值与最小值分别为M，m.若A=｛1｝，且a≥1，记g（a）=M-m，则g（a）的最小值_____________.

分析：本题求最值的前提条件是找出二次函数的三个系数间的关系.深入挖掘函数零点的实质：“方程f（x）= 0有实根⇔函数y=f（x）的图像与x轴有交点⇔函数y=f（x）有零点”.故二次函数f（x）-x=a（x-1）2，利用两个函数相等对应系数相等即可得到a，b，c的关系，进而讨论函数f（x）的最值.这样的问题通过前期课堂教学类似思想的渗透，学生在问题的处理上明显比前一阶段熟练.

课堂类题：已知函数f（x）=ax2+bx+c（a＞0）的零点为x1，x2（x1＜x2），函数f（x）的最小值为y0，且y0∈［x1，x2），则函数y=f（f（x））的零点个数是____________.

分析：函数y=f（x）有两个零点x1，x2（x1＜x2），则可利用二次函数f（x）的零点式将其转化为f（x）=a（x-x1）（x-x2），（a＞0），要求y=f（f（x））=a（f（x）-x1）（f（x）-x2）的零点个数，实际就是求a（f（x）-x1）（f（x）-x2）=0（a＞0）的根的个数，因此f（x）=x1或f（x）=x2，结合条件y0∈［x1，x2），利用数形结合我们就能迎刃而解了.

二、分析思考的重要性

很多数学稍难问题在应试中让学生惊慌不已，使得学生明明可以解决的问题也会因为慌乱而不知所措.笔者在应试反思教学中引导学生回顾如何在应试中加强思考的重要性.

问题2过轴上一动点A（a，0）引抛物线y=x2+1的两条切线AP，AQ，其中P，Q为切点，设切线AP，AQ的斜率分别为k1和k2.

（1）求证：k1k2=-4.

（2）试问：直线PQ是否经过定点？若是，求出该定点坐标；若不是，请说明理由.

分析：解析几何的学习对于学生而言有三个不足，要在解析几何中取得高分，主要有以下几个方面的思考：其一是思维入手角度的思考，笔者以为解析几何大多数问题从各种角度入手是半斤八两的，而且运算程度也差别不大，但是设而不求是入手角度必需依仗的；其二是运算能力，运算能力是除了思考之外的必备基本技能，有些方法的思维途径容易，但是运算要求相对较高；其三是对于问题多解性的反思，对于学生应试中出现的不足，既要分析问题失误的原因，也要分析如何思考优秀的解法，给以学生启发和引导.

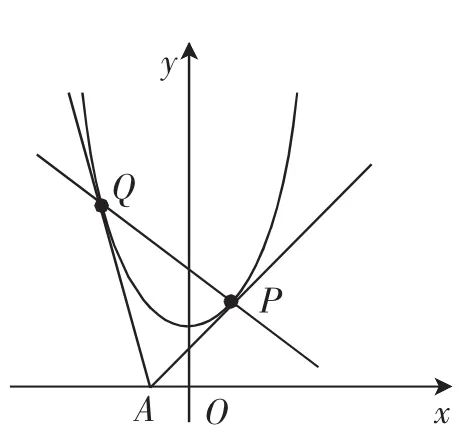
思考1：（1）设过A（a，0）与抛物线y=x2+1的相切的直线的斜率是k，则该切线的方程为y=k（x-a），由得x2-kx+（ka+1）=0，故Δ=k2-4（ka+1）=k2-4ak-4=0，则k1，k2都是方程k2-4ak-4=0的解，故k1k2=-4.

（2）设P（x1，y1），Q（x2，y2），故切线AP的方程是x1x+1，切线AQ的方程是，又由于A点在AP， AQ上，则，所以y1=2x1a+2，y2=2x2a+2，则直线PQ的方程是y=2ax+2，则直线PQ过定点（0，2）.

说明：设直线方程解决解析几何问题是常用的解决方式，从学生应试反馈来看，学生对于判别式为零表示相切的认知较为清晰，但是对于如何利用“算两次”想法去抽离出k1·k2，即韦达定理的体现还是显得不理解，这也正是方程思想的缺失.“算两次”想法与方程思想的培养，是促进学生问题解决理性思维的较好手段，思考（1）中对切线的处理利用了相关结论，并再次利用抽离k1，k2的方程思想解决直线方程进而得到定点.

思考2：（1）如上得：x2-kx+（ka+1）=0，则Δ=k2-4（ka+ 1）=k2-4ak-4=0，于是有，即k1=2a+，故k1k2=-4.直线PQ的方程是y=2ax+2，则直线PQ过定点（0，2）.

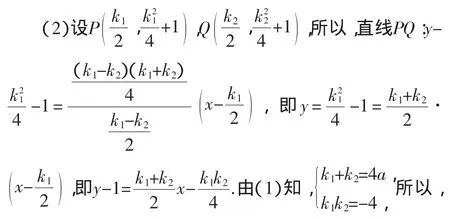
说明：思考（2）的方式，是不少学生使用的，但能得到最终答案的学生是少之又少，这说明处理问题最好的方式依旧是直观，直观思维最大的困难是运算的复杂性，这种处理方式恰是学生应试中使用最多的，但是设而不求思想的缺失大大影响了运算的速度和成功率，教学中对于这种方式的反思是如何引导学生处理方法的选择，通过教学反思引导学生避免对于方程的大量运算是关键.

思考3：（1）设点P（x1，y1），Q（x2，y2），在这两点处的切线分别为l1，l2，设l1：y-y1=k1（x-x1），与抛物线方程联立：x2）（x-x1），由（1）易得PQ：y=（x1+x2）x-x1x2+1=2ax+2，所以直线PQ经过定点（0，2）.

说明：对于问题（1）与（2）的整合处理是思考3的关键，这种思维方式是着眼大处，整体性的思考，对于学生整体问题思维角度的掌握是一种提升，考虑到笔者任教学情程度相对较好，因此问题处理基本围绕后半展开，因此这里所涉及的韦达定理介入恰好整合了问题（1）和（2），成为培养理性思维的更高途径，对于培养学习习惯也是一种历练.

三、反思失分的原因

反思失分原因是提高学生学习习惯，促进理性思维的较好方式.笔者的建议是对于这样的问题，分两步进行，首先请学生重做一遍问题，其次是回忆、厘清应试中犯错的因素，分析错误的原因.通过数次实践，笔者认为，这种方式对于学生促进理性思维和培养学习习惯更有利于学生反思自身的学习和引导教师纠正教学的不足.

（1）当a=0时，求f（x）的极小值；

（2）若存在x1，x2∈［e，e2］，使f（x1）≤f′（x2）+a成立，求实数a的取值范围.

某学生自我剖析：第（1）问由于定义域的问题影响解答的正确性，在第（2）问的求解中，在讨论函数f（x）=的最小值时，需要对非负数a进行分类讨论.而确立分类标准是本题的难点，要根据导函数的正负进行不重不漏地分类讨论，否则，讨论将是不完整的.

教师评析：本题第一小题考查利用导数求函数的极值，第二小题利用存在命题的形式考查含参数函数的最值.第（2）问作为把关题起到了很好的区分作用，存在性问题是教学中的一个难点，试题将两个存在作为问题的出发点首先就“击溃”了一部分学生，即“筛选了一遍”，然后的分类讨论或参变分离都较为复杂，解决起来实属不易.函数导数试题作为压轴题，其考查核心依旧是利用导数的工具来研究函数的单调性、极值、最值等基本性质，其难点并不体现在求导运算上，而是体现在导数作为工具对函数单调性的影响上，即分类讨论的落点上；从另一个角度来说，此题用参变分离的方法似乎优于分类讨论，在教学中需要平衡两种方法的教学.试题充分考查了基本函数性质、“三个二次”的问题等中学核心知识，突出考查了函数与方程、分类与整合、数形结合、化归与转化等基本数学思想，考查了学生的运算能力、思维能力和分析解决问题的能力.

总之，通过应试后的反思教学，一方面可以了解到学生的知识、能力的掌握情况，为日后教师改进教学工作、提高教学质量提供参考依据；另一方面可以反映试卷命题质量，以便日后修改或筛选考试试题，建立试题库和实施标准化考试服务.从一个方面来说，这也将促进中学数学教师的专业化发展.对教师来说，做试卷是“外炼筋骨皮”，而做反思分析则是“内练一口气”，因此，做好反思教学的意义十分重大.

1.乔家瑞.高中数学解题方法与技巧［M］.北京：首都师范大学出版社，2012.

2.李建霞.粤教版高中数学“本章小结”有效教学的探究与实验［J］.数学通报，2013（7）.