训练对于步伐周期长程相关性的影响研究

李鹏斐， 李孟君， 陈曦， 李孟轩， 唐凯

(北京理工大学 机电工程与控制国家级重点实验室， 北京 100081)



训练对于步伐周期长程相关性的影响研究

李鹏斐， 李孟君， 陈曦， 李孟轩， 唐凯

(北京理工大学 机电工程与控制国家级重点实验室， 北京 100081)

为研究普通人群和受训人群步伐特征的差异，设计静电探测器对两种不同人群样本踏步静电信号进行采集，采用消除波动趋势分析法对步伐周期及其相关序列进行分析，研究步伐训练对于步伐相关性的影响. 研究结果表明，步伐训练使受训人员比普通人员的步伐周期增量幅度序列具有更强的长程相关性，而符号序列具有更强的长程反相关性.

步伐静电信号；步伐周期；消除趋势波动分析；步伐训练；长程相关性

随着仿人机器人、人体医疗监测等研究的大量开展，人体步伐规律的研究受到越来越多的重视. 国内外研究机构开展了大量的基于不同测量体制和算法的研究，利用摄像机拍摄研究对象在步行时图像进行分析，以及在人体关键部位固定加速度传感器测量步行过程中的力学信息是研究中最常采用的两种方式[1-3].

近年来，静电传感器因其非接触、无穿戴等优势而获得研究者的青睐，用来获取人步行时的静电信号进行步伐规律研究[4-5]. 李鹏斐等[5]利用静电信号分析多个不同人员的踏步信息，通过长程相关性分析发现，人在踏步时步伐周期序列及其分解得到的增量幅值序列和符号序列存在明显的长时变化规律. 本文将进一步分析不同人群样本的步伐信号，研究步伐周期长时规律的普遍性及步伐训练对于步伐周期长时规律的影响.

1 普通人群步伐周期特性

本文选择步伐周期作为主要参数研究长时间系统训练对于步伐相关性的影响. 为此，分别选取5名普通人员与5名受训人员作为测试样本，普通人员选取在校青年男性学生作为样本. 在测量过程中用原地踏步的信号代替步行信号计算步伐周期，每位测试对象在静电传感器旁原地踏步300 s，通过静电传感器及采集系统记录踏步过程中的步伐静电信号，利用自相关算法计算准确的步伐周期进行分析.

1.1 步伐周期序列分析

为了研究步伐周期长时间的变化规律，采用消除趋势波动分析算法[6](detrended fluctuation analysis， DFA)进行分析. DFA算法通过波动函数F(n)与序列分割区间长度n之间的关系来表征原始序列规律，波动函数的计算公式为

(1)

式中：Nn为以n为长度分割序列所得到的区间数目；Y(i)为时间序列的累积离差；Yv(i)为对区间v内数据点进行拟合后的多项式取值. 经过分析，选取分割区间长度范围为4≤n≤N/8(N为步伐周期序列长度，即总步伐数).

测得的一组步伐周期序列如图1(a)所示，对其进行DFA分析，并将波动函数F(n)与分割区间长度n的关系曲线在双对数坐标系中进行表示，如图1(b)所示.

从图1(b)可以看出，波动函数F(n)与n在双对数坐标系中具有很好的线性关系，即二者存在幂率关系F(n)～nα，其中指数α即为对数据点拟合直线的斜率. 对该被测人员的数据利用最小二乘法进行拟合，可得拟合直线的斜率为α=0.69. 由此可知，波动函数与分割区间长度的关系为F(n)～n0.69.

根据DFA算法，α取值不同，对应时间序列的相关特性也不同. 当0<α<0.5时，时间序列具有持续的反长程相关性，且α越小，反相关性越强；当α=0.5时，时间序列不相关或只具有短程相关性；当0.5<α≤1.0时，时间序列具有持续的长程相关性，且α越大，长程相关性越强. 因此，该步伐周期序列具有持续的长程相关性. 这种长程相关性表明，该人员在踏步过程中，步伐周期虽然一直处于波动状态，但从长时间来看，步伐周期保持较好的稳定性，而并非完全随机变化.

1.2 步伐周期增量序列分解分析

对步伐周期序列中相邻值做差，得到步伐周期增量序列. 将步伐周期增量序列分解为幅值序列和符号序列两个子序列. 幅值序列为周期增量的绝对值序列，符号序列元素为每个增量值的正负，即当增量≥0时定义为+1，<0时为-1. 其中，周期增量幅值序列表示被测人员步伐周期调整的大小，而符号序列则代表步伐周期调整的频率. 对增量幅值序列和符号序列分别进行DFA处理，并对所得结果进行线性拟合，所得结果如图2所示. 两者的标度指数分别为0.53和0.43，说明该人员步伐周期增量的幅值序列和符号序列分别呈现出长程相关性和长程反相关性.

根据以上分别对幅度序列和符号序列的分析结果可知，该人员在踏步过程中，步伐周期调整具有明显的规律. 幅值序列的长程相关性表明其步伐周期在一个大幅值的调整之后较大可能伴随着一个大幅值的调整. 而符号序列的长程反相关性说明一个正向的步伐周期调整之后很可能紧跟着一个反向的调整.

1.3 普遍性分析

为验证该结论的普遍性，分别采集5位普通人员的步伐静电信号，并对其步伐周期序列、步伐周期增量幅值序列和符号序列进行消除趋势波动分析，得到每位被测人员各序列对应的标度指数分别记为α1，α2，α3. 统计结果见表1.

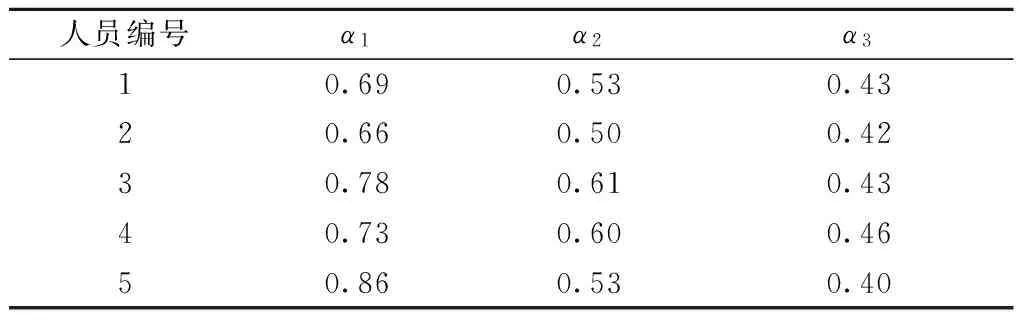
表1 普通人员各序列标度指数

从表1可以看出，以上对普通被测人员的分析结果具有一定的普遍性，即普通人在进行踏步时虽然步伐周期一直处于变化过程，但从长时间来看，其步伐周期保持相对稳定(标度系数大于0.5)，而这种稳定状态是通过不断调节步伐周期大小来实现的. 而调节过程具有明显的规律性，一个大的正向周期增量调整之后，被测人员为了保持步伐稳定很可能伴随着一个较大的负周期增量，而一个小的步伐周期增量之后较大概率伴随着一个较小的反向调整. 这一结果说明人在踏步过程中为了保持一种相对稳定的步伐快慢状态，对步伐周期的调整并非随机过程，而是一种较规则的双向对称调整.

2 受训人员步伐周期特性

在对普通人员的步伐周期长时相关性进行分析后，对受训人员的踏步静电信号进行分析. 受训人员选取经过3年以上系统步伐训练的军校高年级学生，按照前述相同算法，得到受训人员的步伐周期及其相关序列，其中一组步伐周期序列如图3(a)所示.

受训人员步伐周期与普通人员相比，其周期值略大，分布在1.10～1.15 s，但无明显规律. 对该序列进行DFA处理，所得的结果如图3(b)所示. 拟合所得标度指数为0.81，说明该受训人员步伐周期与普通人员类似，呈持续的长程相关性.

由周期序列计算得到步伐周期增量序列，并将其分解为幅度序列与符号序列分别进行分析. 分析结果如图4所示，拟合所得标度指数分别为β=0.71和β=0.36. 结果表明幅值序列具有明显的长程相关性，而符号序列呈现明显长程反相关性.

根据对该受训人员的步伐静电信号分析结果可知，其在踏步时步伐周期及相关序列呈现类似于普通人员的长程规律. 为进一步验证该规律在受训人员中的普遍性，对5名受训人员的步伐静电信号做相同分析，步伐周期序列、周期增量幅值序列和增量符号序列的标度指数分别记为β1，β2，β3，统计结果见表2.

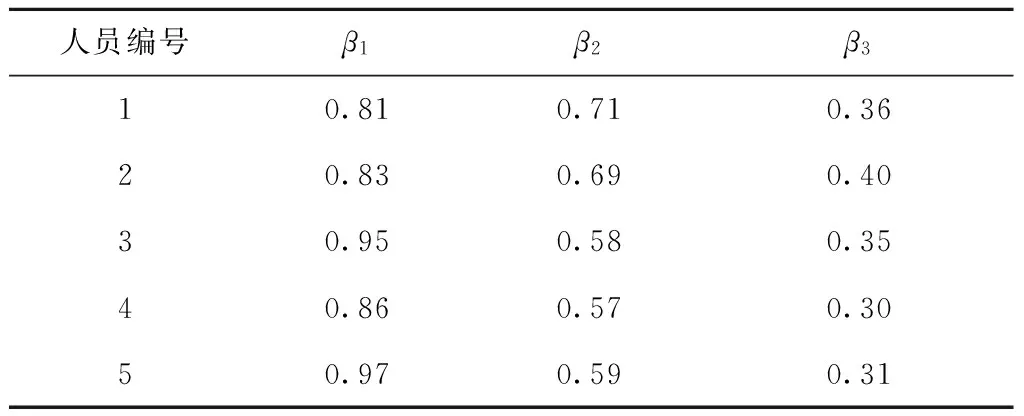
表2 受训人员各序列标度指数

由表2可以看出，所有受训人员步伐周期序列和增量幅值序列均呈现出长程相关性，而周期增量符号序列则具有明显的长程反相关性，该规律具有普遍性.

3 步伐训练对于步伐周期长程相关性的影响

根据以上分析，普通人员和受训人员的步伐周期序列、步伐周期增量幅值序列和增量符号序列均具有相似的长时变化规律. 但对比两组不同人员的具体结果可以发现，受训人员步伐周期和增量幅值序列的标度指数较普通人员的标度指数更大，其步伐周期增量符号序列的标度指数较普通人员更小. 为了更明确地显示这一规律，将两类不同人员的各标度指数进行统计分析，计算其平均值和标准差，统计结果见表3.

表3 两类人员各标度指数对比

Tab.3 Comparison of scaling exponents between ordinary subjects and trained subjects

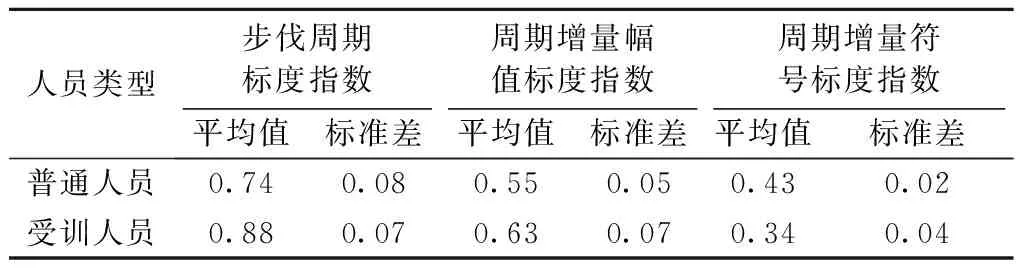
人员类型步伐周期标度指数周期增量幅值标度指数周期增量符号标度指数平均值标准差平均值标准差平均值标准差普通人员0.740.080.550.050.430.02受训人员0.880.070.630.070.340.04

从表3可以看出，受训人员在正常踏步时步伐周期序列的长程相关性标度指数比普通人员大. 这表明相较于普通人员，由于受训人员经历长时间的步伐训练，使得其在踏步时步伐快慢更为稳定，步伐周期的长程相关性更强.

受训人员的步伐周期增量幅度序列标度指数相比普通人员的结果普遍较大，符号序列标度指数比普通人员较小. 这两个指数对比说明，受训人员踏步时对于步伐周期的调整更加频繁且有规律，调整幅度的一致性更强，而普通人员步伐周期调整的幅度长程相关性更弱，调整的随机性更强.

4 结 论

通过对两组不同类型人员(未受步伐训练和受过长时严格步伐训练)踏步静电信号研究发现，被测人员在踏步过程中都是通过不断地调整使得步伐周期保持在一个稳定的数值，并且调整过程是一种双向的对称调整. 但长时间系统性步伐训练使得人在踏步时对于步伐周期进行调整的频率更高，调整的幅度更加稳定. 本研究有助于通过步态和步伐特征对于不同类型人员的识别，结果对于运动神经疾病的早期预测、康复训练和仿人机器人设计具有理论参考价值.

[1] Vega I R， Sarkar S. Statistical motion model based on the change of feature relationships: human gait-based recognition[J]. Pattern Analysis and Machine Intelligence， IEEE Transactions on， 2003，25(10):1323-1328．

[2] Xu D， Yan S， Tao D， et al. Human gait recognition with matrix representation[J]. IEEE Transactions on Circuits and Systems for Video Technology， 2006，16(7):896-903．

[3] Ailisto H J， Lindholm M， Mantyjarvi J， et al. Identifying people from gait pattern with accelerometers[C]∥Defense and Security. International Society for Optics and Photonics， 2005:7-14．

[4] Takiguchi K. The measurement system of human walking[R]. Japan: Information Technology Promotion Agency， 2002.

[5] 李鹏斐，李孟君，陈曦，等.基于静电信号的人体步伐周期长程相关性研究[J].电子学报，2015，43(6):1078-1083.

Li Pengfei， Li Mengjun， Chen Xi， et al. Research on long range characteristics of human gait cycle based on electrostatic signals[J]. Chinese Journal of Electronics， 2015，43(6):1078-1083. (in Chinese)

[6] Peng C K， Buldyrev S V， Havlin S， et al. Mosaic organization of DNA nucleotides[J]. Physical Review E， 1994，49(2):1685.

(责任编辑：刘雨)

Impact of Training on Long-Range Correlation of Gait Cycle

LI Peng-fei， LI Meng-jun， CHEN Xi， LI Meng-xuan， TANG Kai

(State Key Laboratory of Mechatronical Engineering and Control， Beijing Institute of Technology， Beijing 100081， China)

In order to study the difference of gait cycle characteristic between ordinary people and trained people, human gait signal was measured by an electrostatic sensor instead of accelerometer. Self correlation algorithm was applied to obtain the gait cycle series, further to calculate the increment series. The increment series was decomposed into magnitude series and sign series. A detrended fluctuation analysis algorithm was applied to analyze these series for 5 subjects without training and 5 others trained. It is found that the magnitude series of trained subjects show stronger long-range correlation than those without training, and the sign series of trained subjects show stronger long-range anti-correlation than the other.

electrostatic gait signal; gait cycle; detrended fluctuation analysis; gait training; long-range correlation

2015-06-19

国家自然科学基金资助项目(51407009)

李鹏斐(1980—)，男，博士，讲师，E-mail:pfli@bit.edu.cn.

Q 612

A

1001-0645(2016)02-0148-05

10.15918/j.tbit1001-0645.2016.02.008