基于Additive Runge-Kutta方法的激波聚焦起爆高精度数值模拟

王成， 宋清官

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)



基于Additive Runge-Kutta方法的激波聚焦起爆高精度数值模拟

王成， 宋清官

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

基于详细氢氧化学动力学模型，建立了描述氢氧爆轰的多组分反应欧拉方程组. 针对建立的反应欧拉方程组，数值方法上采用3阶Additive Runge-Kutta方法对时间项进行积分，采用5阶精度的加权本质无振荡(WENO)格式对空间对流项进行离散，自主研发了大规模高精度计算程序. 该程序能够处理化学反应源项引起的刚性问题，且能节省计算时间和计算内存. 对半球型、半椭球型、圆锥型3种结构形式凹面腔内的激波聚焦起爆过程进行了数值模拟，数值模拟研究得到了不同结构形式凹面腔内的激波聚焦起爆过程.

详细化学动力学模型； Additive Runge-Kutta方法； WENO格式；激波聚焦

气相爆轰是一个超音速燃烧过程，依靠波阵面后反应区能量的快速释放来自维持，因此气相爆轰是燃料氧气混合物释放燃料化学能极其充分的方式，因而具有较高的能量利用效率[1]. 脉冲爆轰发动机(pulse detonation engine， PDE)利用了气相爆轰的特点，在发动机性能提升方面拥有巨大优势，正逐渐成为了国内外新型发动机研究热点. 爆轰波的点火起爆是脉冲爆轰发动机工作的关键条件，激波聚焦能够在可燃气体中产生高温高压区，进而可以点火起爆形成爆轰波，是脉冲爆轰发动机点火起爆研究的一个重要方向.

国外在20世纪90年代已经开始了激波聚焦方面的研究，且发展较为成熟. Izumi等[2]对惰性激波在抛物形或楔形凹面腔的反射问题进行了实验和数值模拟研究；Levin等[3]提出了基于激波聚焦起爆的两级脉冲爆轰发动机概念，解决了脉冲爆轰发动机的点火起爆问题，并使得提高脉冲爆轰发动机的工作频率成为可能. 国内激波聚焦问题研究起步较晚. 董刚等[4]数值模拟研究了气体反应活性、入射激波强度及反射壁面形状对激波聚焦起爆的影响；曾昊等[5]开展了两级脉冲爆轰发动机的相关研究，数值模拟了凹面腔内的激波聚焦起爆过程，分析了环形射流喷口位置、环形射流初始压力、入射喷口宽度、凹面腔结构对激波聚焦起爆过程的影响，并进行了初步的原理性实验研究，研究了导流角、气流出口面积、扩张角尾喷管、凹面腔与射流入口间距离等对激波聚焦的影响.

为进一步研究凹面腔内的激波聚焦起爆过程，本文基于详细氢氧化学动力学模型[6]，数值方法上采用3阶Additive Runge-Kutta方法对时间项进行积分，空间对流项的离散采用5阶精度的加权本质无震荡(WENO)格式[7]，分别对半球型、半椭球型和圆锥型3种结构的凹面腔的激波聚焦起爆过程进行了数值模拟，对比研究了不同凹面腔结构的激波聚焦规律.

1 控制方程

本文采用多组分反应Euler方程组描述氢氧预混气体的爆轰化学反应过程

(1)

(2)

(3)

(4)

式中：p，ρ，e，T，u，v，h分别为压力、密度、单位质量的总能、温度、x和y方向的速度以及单位质量的焓；Y1，Y2，…，YN-1分别为基元反应各组分的质量分数；R为普适气体常数；ω1，ω2，…，ωN-1分别为各组分的质量生成率.

为准确地描述氢氧预混气体的爆轰反应过程，化学反应模型采用9组分20步基元反应模型[1]. 参与化学反应的各组分分别为 H2，O2，OH，O，H，H2O2，HO2，H2O，此外氢氧预混气体用惰性气体N2稀释，N2不参与化学反应. 化学反应方程可统一写为

(5)

kfm=AmTnmexp-EamR0T，

kpm=exp∑9i=1υ″mi-υ′mis0iRi-hiRiT，

kem=kpmexpp0R0T∑9i=1(υ″mi-υ′mi)，

kbm=kfm/(kem).(6)

(7)

式中：Wi为第i组分的摩尔质量；γTB为第三体效应指数.

2 数值方法

在数值计算方法方面，基于WENO-LF[8]对物理通量进行分裂，方程(1)离散为

(8)

由于化学反应模型采用了9组分20步基元反应模型，对流项与化学反应源项之间，以及各个化学反应源项之间时间尺度差别很大，导致欧拉方程组出现严重的刚性问题. 为了解决刚性问题，本文采用了显隐式Additive Runge-Kutta方法对时间方向进行积分[10]. 该方法能够解决下述形式的常微分方程组：

(9)

式中：F(U)为N项的总和，对于多组分反应欧拉方程组，N=2，即方程右端F(U)包含对流项Fns(U)和化学反应源项Fs(U).

AdditiveRunge-Kutta方法的主要思想是将刚性项Fns(U)和非刚性项Fs(U)分开处理，对非刚性项Fs(U)运用显式Runge-Kutta(ERK)方法进行显式积分，对刚性项Fns(U)运用对角隐式Runge-Kutta(ESDIRK)方法进行隐式积分. s步AdditiveRunge-Kutta法的具体使用方法如下：

(10)

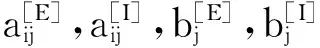
3 计算模型及结果分析

3.1 一维气相爆轰

预混气体H2/O2/N2的体积比为0.50/0.25/0.25，初始温度T0=300 K，初始压力pa=0.101 MPa. 在左侧封闭端设置一段高温高压点火区，点火温度Tin=3 000 K，点火压力pa=0.5 MPa. 数值方法上对于空间对流项的离散采用5阶精度的加权本质无震荡(WENO)格式.

为研究网格尺寸对计算结果的影响，分别取网格尺寸为2.00，1.00，0.50，0.25，0.10，0.05 mm.

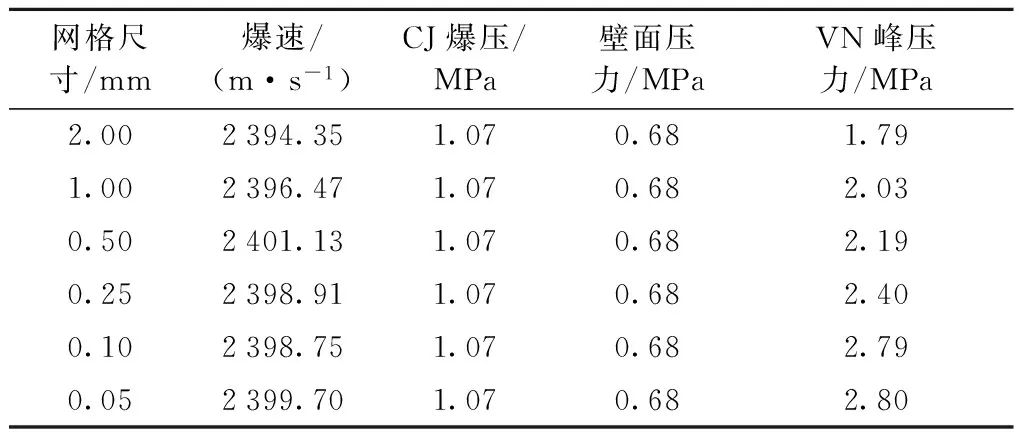
表1 不同网格尺寸下的爆轰参数

从表1中可以看出，平均爆速、CJ爆压和壁面压力在不同网格尺寸下基本趋于相同值，即网格尺寸对其影响不大，且各物理量值与理论值基本吻合；而Von Neumann峰压力随着网格尺寸减小而增大，且随着网格尺寸的减少而收敛. 综上所述，网格尺寸取为0.1 mm时满足计算精度，既能准确的计算各爆轰参数，又能减少网格数，节省计算时间.

选取网格尺寸为0.1 mm，通过对比各组分的体积分数，容易发现各组分变化的量级差别很大，H2，O2，H2O变化的量级为10-1，OH，O，H变化的量级为10-2，H2O2和HO2变化的量级分别为10-4和10-6且衰减很快，如图1(g)～1(h)，因此不同组分在氢氧预混气体爆轰波的化学反应中起的作用并不相同，甚至差别很大，可以忽略对反应影响较小的组分H2O2和HO2，对基元反应模型做进一步简化，简化的化学反应模型应用到下面的激波聚焦起爆研究中.

3.2 激波聚焦起爆

为了研究不同凹面腔结构内的激波聚焦起爆过程，本文选取了半球型、半椭球型和圆锥型3种结构的凹面腔作为计算模型，如下：

工况1：直径为50 mm，开口直径为25 mm的半球凹面腔；

工况2：长径为50 mm，短径为25 mm的半椭球凹面腔；

工况3：高为25 mm，底面圆直径为25 mm的圆锥凹面腔.

凹面腔和尾喷管为内区域(实线)，喷管外为外区域(虚线)，如图2所示. 对于内区域，填充体积比0.23/0.16/0.61的H2/O2/N2预混气体，等截面尾喷管轴线方向长12 mm，环形射流入口为压力入口边界，环形射流入射宽度2.8 mm，压力pin=0.45 MPa，温度Tin=450 K；对于外区域，填充空气，压力pa=0.101 MPa，温度Ta=300 K. 凹面腔及尾喷管为刚性、无滑移、绝热壁面. 数值方法上采用3阶Additive Runge-Kutta方法对时间项进行积分，空间对流项的离散采用5阶精度的加权本质无震荡(WENO)格式. 从初始网格尺寸为0.1 mm. 选取凹面腔中轴线为压力观测线，选取凹面腔中轴线上的点M作为压力观测点，如图2所示.

从图3中可以看出，高温高压的环形射流由入口喷入半球形凹面腔内，初始的温度、压力不足以起爆预混气体，在凹面腔内形成了两道激波，如图3(a)所示. 随着激波的传播，激波的强度逐渐减弱，如图3(b)所示，但是当上下激波相遇碰撞时，压力增加，激波的强度加强，此时仍未能起爆预混气体，如图3(c) 所示.

激波继续向前传播，在半球型壁面处发生反射，由于壁面收敛的作用，压力逐渐增加，形成了更强的激波. 激波继续向前传播，在半球凹面腔中心处发生汇聚，如图3(d)所示，当激波在球形凹面腔中心处发生汇聚时，压力密度等参量急剧增加，达到了氢氧预混气体的临界起爆条件，发生起爆，如图3(e)所示. 起爆之后，爆轰波在球形凹面腔内迅速传播，如图3(f)～3(h)所示，实现了脉冲爆轰发动机的起爆过程.

图3～图6可以看出，对于半球凹面腔，在t=310.72 μs时，在中轴线上发生激波聚焦起爆，起爆压力约为3.0 MPa；对于半椭球凹面腔，在t=330.05 μs时，在中轴线上发生激波聚焦起爆，起爆压力约为2.5 MPa；对于圆锥凹面腔，在t=307.77 μs时，在中轴线附近上发生激波聚焦起爆，起爆压力约为2.0 MPa，同时发现初始起爆点明显位于中轴线偏上的位置，本文中给出的入流条件和物理模型均是关于中轴线对称的，由此推测这种现象是圆锥凹面腔顶点的奇异性导致的数值误差造成的.

通过对比3种结构的凹面腔的激波聚焦过程，发现在此初始条件下，3种结构的凹面腔均实现了激波聚焦起爆过程，且聚焦中心基本均位于中轴线上，壁面收敛导致的激波增强效果不足以起爆预混气体. 由于半椭球凹面腔的曲率要比半球凹面腔和圆锥凹面腔的曲率要大，因此半椭球凹面腔的激波聚焦效果最为明显，聚焦中心位置最为靠前，如图3～7所示. 此外，通过对比发现，3种结构的凹面腔实现聚焦起爆时间不同，其中圆锥凹面腔最早实现聚焦起爆，半球凹面腔次之，半椭球凹面腔最晚实现聚焦起爆.

此外本文还研究了不同凹面腔结构对脉冲爆轰发动机工作频率的影响. 由分析可知，凹面腔内预混气体起爆之后产生大量高温高压气体，气体由尾喷管喷出形成推力，气体喷出后在凹面腔内形成了低温低压区，此时入口处的气体总压要高于凹面腔内的气体总压，此时高温高压的射流再次由入口进入凹面腔内，再次实现聚焦爆轰过程，进入下一个循环，因此凹面腔内形成了周期性的脉冲爆轰波，实现了循环起爆. 从图中容易看出，对于3种结构的凹面腔，观测点M的压力均在400 μs后发生了周期性的变化，因此对于3种结构的凹面腔，起爆之后均实现了循环起爆. 其中，半球凹面腔的工作频率约为16.7 kHz，半椭球凹面腔的工作频率约为15.0 kHz，圆锥凹面腔的工作频率约为20.0 kHz，即圆锥凹面腔的工作频率最高，半球凹面腔的工作频率次之，半椭球凹面腔的工作频率最低.

4 结 论

采用3阶Additive Runge-Kutta方法对时间项进行积分，空间对流项的离散采用5阶精度的加权本质无震荡(WENO)格式，对脉冲爆轰发动机激波聚焦起爆过程进行了数值模拟，重点研究了半球凹面腔、半椭球凹面腔和圆锥凹面腔对激波聚焦起爆过程的影响，并得到了以下结论:

① 3种结构的凹面腔均实现了激波聚焦起爆过程，且聚焦中心基本均位于中轴线上，其中半椭球凹面腔的激波聚焦效果最为明显，聚焦中心位置最为靠前，因此为获得明显的聚焦效果，应使用半椭球凹面腔；

② 3种结构的凹面腔实现聚焦起爆时间不同，其中圆锥凹面腔最早实现聚焦起爆，半球凹面腔次之，半椭球凹面腔最晚实现聚焦起爆，因此为较快实现聚焦起爆，应使用圆锥凹面腔；

③ 3种结构的凹面腔均实现了循环起爆，其中，圆锥凹面腔的工作频率最高，半球凹面腔的工作频率次之，半椭球的工作频率最低，因此为达到较高的工作频率，应使用圆锥凹面腔.

[1] 张博，白春华.气相爆轰动力学特征研究进展[J].中国科学：物理学 力学 天文学，2014，44(7):665-681.

Zhang Bo， Bai Chunhua. Research progress on the dynamic characteristics of gaseous detonation[J]. Scientia Sinica: Physica， Mechanica & Astronomica， 2014，44(7):665-681. (in Chinese)

[2] Izumi K， Aso S， Nishida M. Experimental and computational studies focusing processes of shock waves reflected from parabolic reflectors[J]. Shock Waves， 1994，3(3):213-222．

[3] Levin V A， Nechaev J N， Tarasov A I. A new approach to organizing operation cycles in pulse detonation engines[C]∥Proceedings of High-Speed Deflagration and Detonation: Fundamentals and Control. Moscov: [s.n.], 2001:31-44.

[4] 董刚，唐敖，叶经方，等.激波聚焦诱导点火和爆轰的数值研究[J].爆炸与冲击，2006，25(5):437-444.

Dong Gang， Tang Ao， Ye Jingfang， et al. Numerical studies on initiation and detonation induced by shock wave focusing[J]. Explosion and Shock Waves， 2006，25(5):437-444. (in Chinese)

[5] 曾昊，何立明，章雄伟，等.环形射流喷口位置对激波聚焦起爆的影响分析[J].推进技术，2011，32(3):437-442.

Zeng Hao， He Liming， Zhang Xiongwei， et al. Investigation on the influence of jets spout location on detonation initiation via imploding annular shock waves[J]. Journal of Propulsion Technology， 2001，32(3):437-442. (in Chinese)

[6] 赵慧，李健，郝莉.不同曲率弯管对气相爆轰波传播特性的影响[J].北京理工大学学报，2014，34(增刊1):176-180．

Zhao Hui， Li Jian， Hao Li. The influence of different bend curvature on gaseous detonation wave propagation[J]. Transactions of Beijing Institute of Technology， 2014，34(suppl 1):176-180. (in Chinese)

[7] 蔺伟，宋清官，王成，等.浓度梯度对瓦斯爆炸影响的数值模拟[J].北京理工大学学报，2015，35(4):336-340.

Lin Wei， Song Qingguan， Wang Cheng， et al. Numerical investigation about the effect of concentration gradient on methane explosion[J]. Transactions of Beijing Institute of Technology， 2015，35(4):336-340. (in Chinese)

[8] Jiang G S， Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics， 1996，126(1):202-228．

[9] Chi-Shu W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[J]. Lecture Notes in Mathematics， 1998，1697(1):325-432.

[10] Kennedy C A， Carpenter M H. Additive Runge-Kutta schemes for convection diffusion reaction equations[J]. Applied Numerical Mathematics， 2003，44(1-2):139-181.

(责任编辑：刘雨)

Numerical Application of Additive Runge-Kutta Methods on Detonation Initiation with Convergence of Shock Waves

WANG Cheng， SONG Qing-guan

(State Key Laboratory of Explosion Science and Technology， Beijing Institute of Technology， Beijing 100081， China)

Based on detailed hydrogen and oxygen chemical kinetics model, the multi-species reactive Euler equations were established to describe the hydrogen and oxygen detonation. Using third-order Additive Runge-Kutta methods in time discretization, using fifth-order weighted essentially non-oscillatory (WENO) scheme in spatial discretization, a high-solution large-scale program was developed. It was verified that the program could solve stiff source term caused by multispecies chemical reaction, which could also save computation time and computation memory. With this program, the process of detonation initiation with convergence of shock waves was numerically simulated for 3 types of concave cavity, hemispherical concave cavity, semi-ellipsoidal concave cavity and conical concave cavity. The simulation results show the characteristic of detonation initiation in different types of concave cavity.

detailed chemical kinetics model; Additive Runge-Kutta methods; weighted essentially non-oscillatory scheme; convergence of shock waves

2015-10-30

国家自然科学基金资助项目(11325209，11272056)

王成(1972—)，男，教授，博士生导师，E-mail：wangcheng@bit.edu.cn.

O 383

A

1001-0645(2016)02-0137-07

10.15918/j.tbit1001-0645.2016.02.006