正定Hermite矩阵流形上代数Lyapunov方程的信息几何算法

邵水布， 张二川， 孙华飞

(北京理工大学 数学与统计学院， 北京 100081)



正定Hermite矩阵流形上代数Lyapunov方程的信息几何算法

邵水布， 张二川， 孙华飞

(北京理工大学 数学与统计学院， 北京 100081)

对于正定Hermite矩阵流形上的代数Lyapunov方程AHX+XA+P=0， 基于流形的黎曼几何结构， 作者以矩阵-AHX-XA和P之间的测地距离为目标函数， 提出了代数Lyapunov方程数值解的信息几何算法. 最后，给出了正定Hermite矩阵流形上的代数Lyapunov方程的数值模拟结果．

代数Lyapunov方程; 信息几何算法; 正定Hermite矩阵; 测地距离

许多工程和数学问题， 如信号处理、机器人控制、计算机图像处理[1]等， 最终都可以简化为求解如下代数Lyapunov方程的数值解，

(1)

式中：P为正定Hermite矩阵；AH为矩阵A的共轭转置.

(2)

本文中，考虑正定Hermite矩阵流形上的代数Lyapunov方程的数值解. 方程(1)的解被描述为矩阵-AHX-XA尽可能接近正定Hermite矩阵P，并且它们之间的距离函数采用正定Hermite矩阵流形上的测地距离， 以此为目标函数提出信息几何算法. 最后， 数值模拟结果说明了提出的几何算法的有效性．

1 正定Hermite矩阵流形的几何结构

若n×n的复矩阵A满足AH=A且对任意的非0复矩阵X满足XHAX>0，则称A为正定Hermite矩阵. 所有n×n的正定Hermite矩阵全体构成一个正定Hermite矩阵流形H(n)，用Ekl表示第k行第l列为1，其余元素为0的基本矩阵，则流形H(n)的基底矩阵可以表示为

(3)

式中：i2=-1；p为由数对(k，l)按照某种赋值规则得到的，则任意的正定Hermite矩阵Q∈H(n)可以表示为

(4)

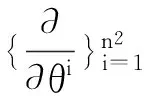
定义1[5]若g表示正定Hermite矩阵流形H(n)上的黎曼度量，对于Q∈H(n)，切空间TQH(n)上的内积定义为

(5)

式中M，N∈TQH(n).

易证， 上述定义的度量满足黎曼度量的基本性质并且在切空间的基底变换下保持不变．

定义2[6-7]令γ:[0，1]→M表示流形M上逐段光滑的曲线，则定义γ的长度为

(6)

任意两点x，y∈M之间的距离定义为连接这两点曲线(如果存在这样的曲线)长度的下确界， 即

(7)

命题1[5-7]正定Hermite矩阵流形H(n)上，对于定义的黎曼度量(5)，则得到经过点Q且沿X方向的测地线

(8)

于是， 根据式(7)得到连接两点Q1，Q2的测地距离

(9)

根据Hopf-Rinow定理，可以知道正定Hermite矩阵流形是测地完备的，即对于任意两点Q1，Q2∈H(n)，都存在连接它们的测地线．

2 正定Hermite矩阵流形上的代数Lyapunov方程

考虑正定Hermite矩阵流形上的代数Lyapunov方程(1)的解，将方程(1)的解描述为在流形H(n)上寻找正定Hermite矩阵X，使得矩阵-AHX-XA尽可能接近P(参见图1)．

为了刻画矩阵-AHX-XA和P之间的距离，选取它们之间的测地距离为两矩阵之间的度量，即目标函数为

(10)

则方程(1)的最优解满足

(11)

为了提出基于下降梯度的信息几何算法，介绍下面的引理.

引理1[8]设f(X)是n阶矩阵X的数量函数，若df(X)=tr(WdX)成立，则函数f(X)关于矩阵X的梯度∂Xf(X)为

(12)

定理1 设J(X)是按式(10) 定义的函数，则J(X)关于正定Hermite矩阵X的梯度为

(13)

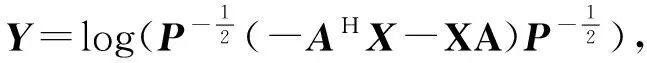
于是，

dJ(X)=d(tr(YHY))=tr(dYHY+YHdY).

根据引理1，目标函数J(X)关于X的梯度为

证毕.

定理2 对于在正定Hermite矩阵流形上， 基于下降梯度的信息几何迭代算法的迭代公式为

(14)

按照正定Hermite矩阵流形上的黎曼指数映射易得上述结论．

根据以上的讨论，给出求解正定Hermite矩阵流形上Lyapunov方程数值解的信息几何算法．

对于正定Hermite矩阵流形H(n)，代数Lyapunov方程(1)的信息几何迭代算法如下:

① 输入初始矩阵X0，步长μ和计算的允许误差界ε>0;

② 按照式(13)计算目标函数J(X)的梯度∂XJ(X);

③ 如果J(X)<ε，则停止迭代输出结果;

④ 按照式(14)更新X并返回步骤②．

3 数值模拟

现考虑正定Hermite矩阵流形上的代数Lyapunov方程

AHX+XA+P=0，

式中：

数值模拟中取初始矩阵X0为

步长μ=0.1， 则在计算误差限ε=10-4的情况下经过71步迭代得到最优解为

实际这个例子中，正定Hermite矩阵流形上Lyapunov方程的精确解为

于是得到误差矩阵的谱半径随迭代步数增加的趋势图(如图2所示).

进一步对比不同步长下的算法计算效率，图3中的曲线分别对应步长μ=0.1，0.2，0.3时，目标函数J(X)和迭代次数的下降关系，其迭代次数分别为39，23，15．

从图3中可以看出步长μ较小， 算法迭代步数多， 收敛相对较慢. 但步长不宜过长， 模拟结果表明， 步长过长容易造成算法发散. 因此， 在实际计算当中可适当调整步长参数以获得合适的收敛速度．

4 结 论

文中作者考虑了正定Hermite矩阵流形上的代数Lyapunov方程的数值解， 以矩阵-AHX-XA和P之间的测地距离为目标函数， 基于下降的黎曼梯度提出求解该问题的信息几何算法. 最后，用数值模拟的结果说明了提出算法的有效性. 类似于文献[5-6]的讨论可以验证， 信息几何算法明显优于其它算法．

[1]CohnSE，ParrishDF.ThebehaviorofforecastcovariancesforaKalmanfilterintwodimensions[J].MonWeaRev， 1991，119(8):1757-1785.

[2]RanACM，ReuringsMCB.Afixedpointtheoreminpartiallyorderedsetsandsomeapplicationstomatrixequations[J].ProcAmMathSoc， 2003，132:1435-1443.

[3]LiJR，WhiteJ.Low-ranksolutionofLyapunovequations[J].SIAMJMatrixAppl， 2002，24(1):260-280.

[4]JbilouK.ADIpreconditionedKrylovmethodsforlargeLyapunovmatrixequations[J].LinearAlgAppl， 2010，432(10):2473-2485.

[5]DuanX，SunH，PengL，etal.AnaturalgradientdescentalgorithmforthesolutionofdiscretealgebraicLyapunovequationsbasedonthegeodesicdistance[J].AppliedMathematicsandComputation， 2013，219(19):9899-9905.

[6]DuanX，SunH，ZhangZ.AnaturalgradientalgorithmforthesolutionofLyapunovequationsbasedonthegeodesicdistance[J].JournalofComputationalMathematics， 2014，32(1):93-106．

[7]LuoZ，SunH.ExtendedHamiltonianalgorithmforthesolutionofdiscretealgebraicLyapunovequations[J].AppliedMathematicsandComputation， 2014，234:245-252．

[8]ZhangX.Matrixanalysisandapplication[M].Beijing:TsinghuaandSpringerPublishingHouse， 2004．

(责任编辑：李兵)

An Information Geometric Algorithm for Algebraic Lyapunov Equation on Positive-Definite Hermitian Matrix Manifold

MUHAMMADShoaibArif，ZHANGEr-chuan，SUNHua-fei

(School of Mathematics and Statistics， Beijing Institute of Technology， Beijing 100081， China )

For the algebraic Lyapunov equation AHX+XA+P=0 on the positive-definite Hermitian matrix manifold， the information geometric algorithm for the numerical solution of the algebraic Lyapunov equation was given via the Riemannian geometric structure of the manifold. In this algorithm， the geodesic distance between the matrix -AHX-XAandPwasadoptedasthecostfunction.Finally，theinformationgeometricalgorithmwasillustratedforthealgebraicLyapunovequationonthepositive-definiteHermitianmatrixmanifoldbysomenumericalsimulationexamples．

algebraicLyapunovequation;informationgeometricalgorithm;positive-definiteHermitianmatrix;geodesicdistance

2014-10-07

国家自然科学基金资助项目(61779031，10932002)

邵水布(1982—)， 男， 博士生，E-mail：shoaib@bit.edu.cn.

孙华飞(1958—)，男，教授，博士生导师，E-mail：huafeisun@bit.edu.cn .

O

A

10.15918/j.tbit1001-0645.2016.02.019