弹道极限速度试验值异常性检验方法研究

赵晓旭， 王树山， 徐豫新

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；2.首都师范大学 信息工程学院， 北京 100048)



弹道极限速度试验值异常性检验方法研究

赵晓旭1，2， 王树山1， 徐豫新1

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；2.首都师范大学 信息工程学院， 北京 100048)

针对基于量纲分析获得弹道极限速度计算模型函数基础上通过若干试验值拟合获得计算模型的方法，研究弹体侵彻靶体试验所获弹道极限速度试验值异常性的检验方法. 根据统计学原理，提出了特定置信水平下标准化残差值在标准正态分布置信区间落入度的弹道极限速度试验值检验方法；同时，进行了3.0，4.5，6.0，7.5，9.0，10.0 g共6种质量35CrMnSi钢FSP弹体对4 mm和5 mm两种厚度典型高强度低合金(HSLA)钢板的侵彻试验，获得了12个弹道极限速度试验值，基于量纲分析及试验数据获得了相应的弹道极限速度计算模型；并以此模型为实例，根据95%置信水平下标准化残差值在(-1.96，1.96)区间落入度进行了弹道极限速度计算模型的检验和修正，研究结果表明所提方法可用于弹道极限速度试验值异常性的检验.

终点效应；数理统计；弹道极限速度；残差

弹道极限速度(v50)是指弹体在特定着角条件下50%概率贯穿一定厚度靶体的入射速度，表现为统计学意义上的弹体贯穿速度，作为材料和结构抗弹体侵彻性能的重要表征参量，在军用和警用装甲防护中得到广泛应用[1-2]. 长期以来，关于不同弹靶材料之间弹道极限速度的试验和理论模型研究一直都是研究的热点[3-6]. 这些研究中，弹道极限速度计算模型获取的最常见办法是基于量纲分析后得到相应的计算模型函数，并基于试验获得若干弹道极限速度后拟合获得计算模型[7]. 拟合获得计算模型计算精度的检验标准通常是用若干个试验点处计算值与试验值相对统计误差的极差值(极差又称全距，是用来表示统计资料中的变异量数，即最大值减最小值后所得之数据)规定的.

在实际应用中，存在两个问题：① 同一极差值下，随着弹道极限速度的提高，由极差值产生的允许区间将增加，如：规定极差值不超过15%，1 000 m/s弹道极限速度的允许区间为150 m/s，100 m/s弹道极限速度的允许区间仅为15 m/s，因基数的不同造成在弹道极限速度较低时过于严格，在弹道极限速度较高时过于宽松；②在实际的试验中，由于装药量、弹体着角等客观因素的影响，试验结果会存在随机性，且弹道极限速度本身就是50%穿透概率下的特征撞击速度，试验点可能存在异常，但异常试验点尚无法发现，这就会使拟合获得计算模型的适用度难以明确.

本工作基于数理统计的方法提出特定置信水平下标准化残差值在标准正态分布置信区间落入度的弹道极限速度试验值异常试验点检验方法. 为了检验该方法的合理性，通过试验获得了3.0，4.5，6.0，7.5，9.0，10.0 g共6种质量35CrMnSi钢FSP弹体对4 mm和5 mm两种厚度典型高强度低合金(HSLA)钢板的弹道极限速度，基于量纲分析和试验数据获得了弹道极限速度计算模型，采用所提方法检验出了试验异常点，并进行了计算模型的修正.

1 检验方法

在数理统计中，残差是指实际观察值与估计值(拟合值)之间的差值. 在回归分析中，测定值与按回归方程预测的值之差，即为残差，残差遵从正态分布. 显然，有多少个数据，就有多少个残差，即可根据多个残差获取残差的数字特征. 定义标准化残差为残差与残差均值之差与残差标准差的比值，即

(1)

残差蕴含了有关模型基本假设的重要信息，对于通过回归分析获得的数学模型，实质是用连续曲线近似地刻画或比拟平面上离散点组，以表示坐标之间函数关系的一种数据处理方法. 残差分析就是利用残差表征数据点与它在回归直线上相应位置的差异信息，来考察模型假设的合理性及数据的可靠性. 因此，可以根据试验数据和基于试验数据拟合获得的模型，通过计算获得残差值和标准化残差值. 因残差服从正态分布，因此标准化残差值服从标准正态分布，可根据标准正态分布表获得标准化残差值落在(-A，A)区间以外的概率为p≤a. 那么，根据统计学原理，若某一变量的标准化残差值落在(-A，A)区间以外，则可在(1-a)×100%置信度将其判为异常试验点，不参与回归拟合. 若A=1.645时，a=0.1；A=1.96时，a=0.05；A=2.24时，a=0.025.

2 方法应用实例

为了进行上述方法的适用性验证，设计了长径比在1.50～1.68的3.0，4.5，6.0，7.5，9.0，10.0 g共6种质量35CrMnSi钢质FSP弹体对4 mm和5 mm两种厚度典型高强度低合金(HSLA)钢板(屈服强度：498.75 MPa，拉伸强度：585.00 MPa)的垂直(即着角为0°)侵彻试验，按常用6射弹法获得了12个弹道极限速度的试验值，列于表1中.

根据量纲分析可得

(2)

式中：dp为FSP直径；Lp为长度；vp为弹速；vt为靶体运动速度；Ht为靶体厚度；φ为弹体的着角；ρp，Ep，Yp和ρt，Et，Yt分别为假设弹体和靶体材料的惯性和强度由密度、弹性常数和屈服极限. 因为弹体和靶体均为钢质，弹体速度远低于材料声速，可认为材料的可压缩性并不重要[8-12].

根据上述具体试验问题，弹、靶材料确定，靶体速度为0，弹体着角为0°，则式(2)可简化为

(3)

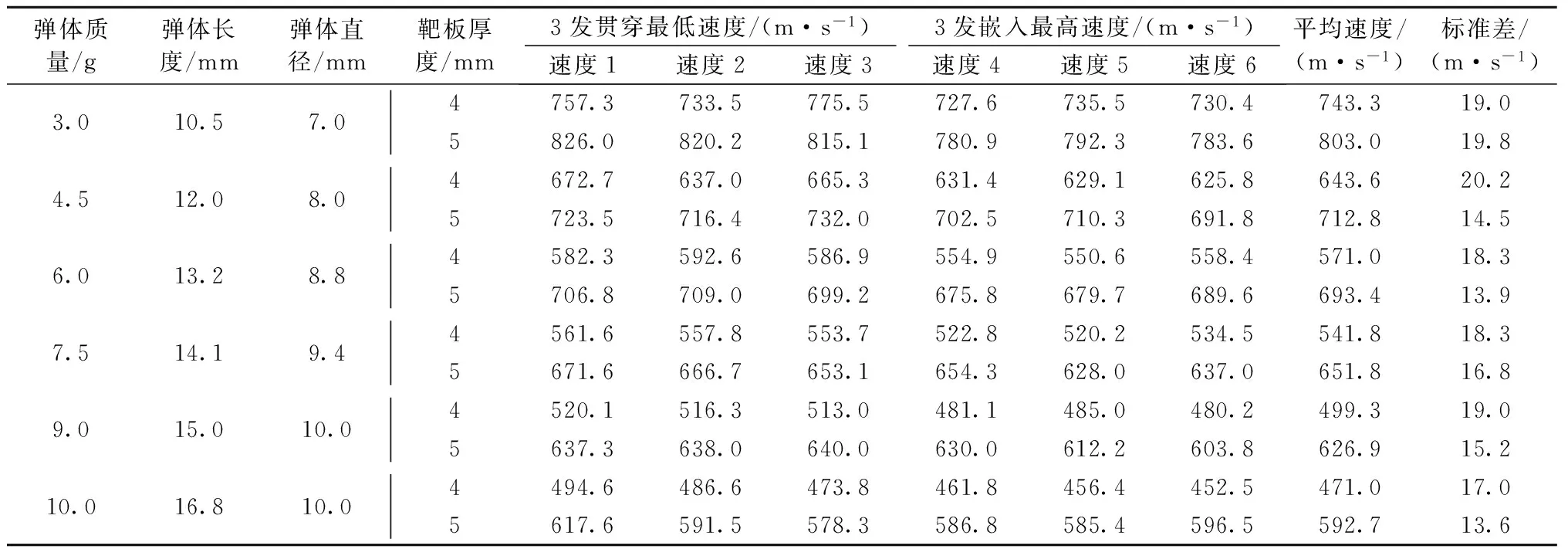
表1 弹体侵彻钢板试验数据

由弹体尺寸可知，弹体长径比相差不大，则长径比可认为常数，根据试验结果可以获得弹道极限速度随弹靶相对厚度的变化关系. 根据试验获得的弹道极限速度采用最小二乘法进行曲线拟合，获得弹道极限速度与弹靶相对厚度的变化关系曲线，如图1所示.

拟合曲线可得到的弹道极限速度计算模型式为

(4)

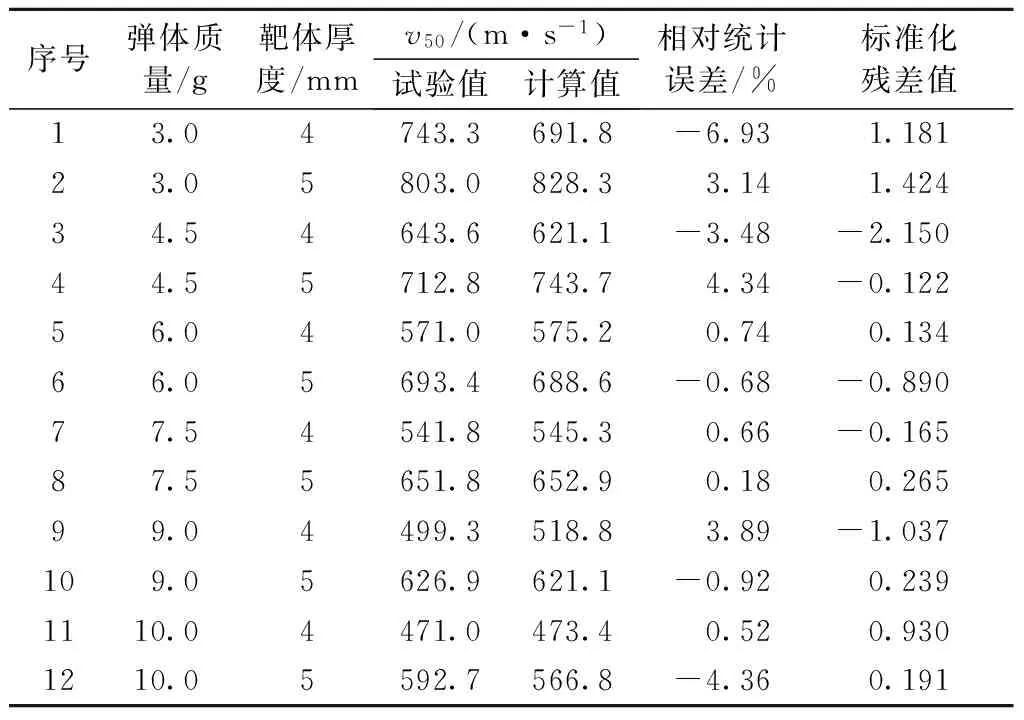
根据试验值和计算模型式(4)，采用上述方法对弹道极限速度试验值异常性进行检验，具体如下：将试验值、式(4)计算所得的弹道极限速度、相对统计误差以及标准化残差值列于表2中.

由表2可见，式(4)计算结果与试验结果的相对统计误差最大为4.34%，最小为-6.93%，相对统计误差的极差值为11.27%，小于一般标准15%，表明计算模型具有可靠性；但从标准化残差值可以看出4.5 g FSP弹体侵彻4 mm厚靶体的标准化残差值为-2.15，落在了95%置信度所规定的(-1.96，1.96)区间以外，如图2所示.

Tab.2 Comparison of experiment data and calculation data from equation (4)

序号弹体质量/g靶体厚度/mmv50/(m·s-1)试验值计算值相对统计误差/%标准化残差值13.04743.3691.8-6.931.18123.05803.0828.33.141.42434.54643.6621.1-3.48-2.15044.55712.8743.74.34-0.12256.04571.0575.20.740.13466.05693.4688.6-0.68-0.89077.54541.8545.30.66-0.16587.55651.8652.90.180.26599.04499.3518.83.89-1.037109.05626.9621.1-0.920.2391110.04471.0473.40.520.9301210.05592.7566.8-4.360.191

虽然该点计算值与试验值的相对统计误差仅为-3.48%，并非最小相对统计误差值，但按上述标准化残差值在标准正态分布置信区间落入度的检验方法，可将该点判定为试验异常点，不参与曲线回归拟合；去掉该点重新拟合曲线，获得计算模型为

(5)

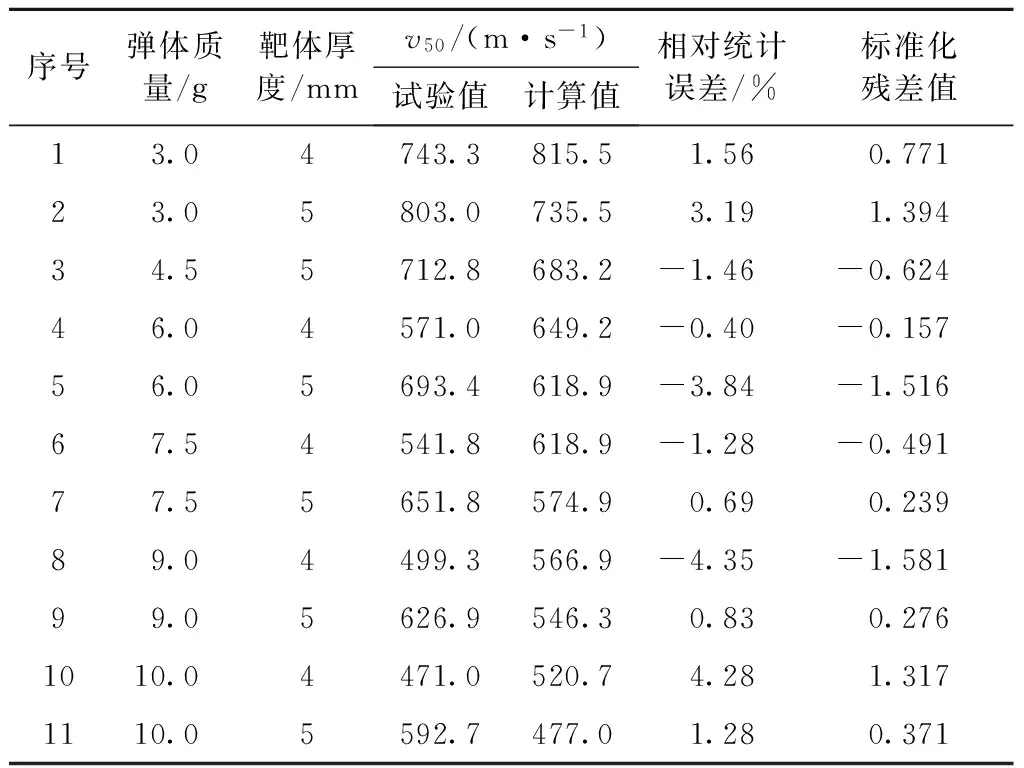
将式(5)的计算得到的弹道极限速度与试验值进行对比，列于表3中.

表3 式(5)计算值与试验值对比

Tab.3 Comparison of experiment data and calculation data from equation (5)

序号弹体质量/g靶体厚度/mmv50/(m·s-1)试验值计算值相对统计误差/%标准化残差值13.04743.3815.51.560.77123.05803.0735.53.191.39434.55712.8683.2-1.46-0.62446.04571.0649.2-0.40-0.15756.05693.4618.9-3.84-1.51667.54541.8618.9-1.28-0.49177.55651.8574.90.690.23989.04499.3566.9-4.35-1.58199.05626.9546.30.830.2761010.04471.0520.74.281.3171110.05592.7477.01.280.371

由表3可见，所有计算点的标准化残差值均落在了(-1.96，1.96)区间以内，且式(5)计算结果与试验值相对统计误差最大为4.28%，最小为-4.35%，相对统计误差的极差为8.63%，与式(4)的极差11.27%相比显著减小，减小幅度为23.4%. 因此，可以认为式(5)比式(4)有更高的计算精度. 但4.5 g弹体侵彻4 mm厚靶体的试验值是弹靶本身随机性太大、试验测试异常等原因造成，还是因为计算模型函数不够合理、覆盖面有限造成，尚不能从已有的试验数据确定，需要进一步试验研究；因无充足的试验数据支持，在此不做深入讨论.

本方法主要用于基于量纲分析获得弹道极限速度计算模型函数基础上通过若干试验值拟合获得计算模型研究过程中试验值异常性的检验，只要弹道极限速度离散试验点不小于9个[13]，满足标准化残差值计算要求，即可用此方法进行检验，方法所用数据来源于试验，本身不受弹靶结构尺寸限制，具有通用性.

3 结 论

针对传统基于量纲分析获得弹道极限速度计算模型函数基础上通过若干试验值拟合获得计算模型精度检验的不足以及弹道极限速度试验值异常点检验方法尚无的实际情况，借鉴数理统计原理，结合具体实践进行了特定置信水平下标准化残差值在标准正态分布置信区间落入度的弹道极限速度试验值检验方法研究，具体结果如下：

① 提出了特定置信水平下标准化残差值在标准正态分布置信区间落入度的弹道极限速度试验值检验方法，并进行实践检验，验证了方法的可行性；

② 通过试验获得了长径比在1.50～1.68的共6种质量35CrMnSi钢FSP弹体对4 mm和5 mm两种厚度典型高强度低合金(HSLA)钢板垂直侵彻的弹道极限速度，基于理论分析获得相应的弹道极限速度计算模型.

[1] 彭刚，王梅，冯家臣，等.弹道极限速度v50在材料抗弹性能评价中的应用研究[J].警察技术，2011，27(2)：12-15.

Peng Gang， Wang Mei， Feng Jiachen， et al. Application study of ballistic limit velocityv50used in anti-projectile performance evaluation[J]. Police Technology， 2011，27(2)：12-15.(in Chinese)

[2] Czarnecki G J. Estimation of thev50using semi-empirical(1-point) procedures[J]. Composites Part B: Engineering， 1998，29(3)：321-329.

[3] Backman M E， Goldsmith W. The mechanics of penetration of projectiles into targets[J]. International Journal of Engineering Science， 1978，16:1-99.

[4] 午新民.钨合金球体对有限厚靶板侵彻的理论与试验研究[D].北京：北京理工大学，1999．

Wu Xinmin. The theoretical and experimental research on tungsten alloy sphere penetrating limited thickness plate[D]. Beijing: Beijing Institute of Technology， 1999. (in Chinese)

[5] 王海福，刘志雄，冯顺山.钢球侵彻钛合金靶板弹道极限速度[J].北京理工大学学报，2003，23(2)：162-164．

Wang Haifu， Liu Zhixiong， Feng Shunshan. Ballistics limit velocity for spherical steel fragments penetrating titanium-alloy target plates[J]. Transactions of Beijing Institute of Technology， 2003，23(2)：162-164. (in Chinese)

[6] Anderson C E Jr，Hohler V，Walker J D， et al. Time-resolved penetration of long rods into steel targets[J]. International Journal of Impact Engineering， 1995，16(1)：1-18.[7] 兰彬，文鹤鸣.钨合金长杆弹侵彻半无限钢靶的数值模拟及分析[J].高压物理学报，2011，22(3)：245-252．

Lan Bin， Wen Heming. Numerical simulation and analysis of the penetration of tungsten-alloy long rod into semi-infinite[J]. Chinese Journal of High Pressure Physics， 2011，22(3)：245-252.(in Chinese)

[8] 徐豫新，王树山，伯雪飞，等.钨合金球形破片对低碳钢的穿甲极限[J].振动与冲击，2011，30(5)：192-195．

Xu Yuxin， Wang Shushan， Bo Xuefei， et al. Armor-piercing ultimate of tungsten alloy spherical fragment against low-carbon steel[J]. Journal of Vibration and Shock， 2011，30(5)：192-195. (in Chinese)

[9] 徐豫新，韩旭光，赵晓旭，等.钨合金高弹速侵彻低碳钢板失效行为试验研究[J].稀有金属材料与工程(已录用).

Xu Yuxin， Han Xuguang， Zhao Xiaoxu， et al. Experimentation researchon failure behavior of tungsten alloy penetrating low carbon steel plate at high velocity[J]. Rare Metal Materials and Engineering (in Press). (in Chinese)

[10] 赵晓旭，王树山，徐豫新，等.钨球高速侵彻低碳钢板成坑直径的计算模型[J].北京理工大学学报,2015,35(12):1217-1221.

Zhao Xiaoxu， Wang Shushan， Xu Yuxin， et al. A crater diameter calculation model of tungsten sphere impacting low carbon steel plate at high velocity[J]. Transactions of Beijing Institute of Technology, 2015,35(12):1217-1221. (in Chinese)

[11] Westerling L， Lundberg P， Lundberg B. Tungsten long-rod penetration into conbined cylinders of boron carbide at and above ordnance velocities[J]. International Journal of Impact Engineering， 2001，25:703-714．

[12] 陈刚，陈小伟，陈忠富，等.A3钢钝头弹撞击45钢板破坏模式的数值分析[J].爆炸与冲击，2007，27(5)：390-397．

Chen Gang， Chen Xiaowei， Chen Zhongfu， et al. Simulations of A3 steel blunt projectiles impacting 45 steel[J]. Explosion and Shock Waves， 2007，27(5)：390-397.(in Chinese)

[13] 王文周.小样本检验法[J].西华大学学报:自然科学版，2005，24(1)：80-82．

Wang Wenzhou. A new approach of small sample test[J]. Journal of Xihua University: Natural Science ed， 2005，24(1)：80-82. (in Chinese)

(责任编辑：刘雨)

Research on Validation Method of Ballistic Limit Velocity Experiment Data Abnormality

ZHAO Xiao-xu1，2， WANG Shu-shan1， XU Yu-xin1

(1.State Key Laboratory of Explosion Science and Technology， Beijing Institute of Technology， Beijing 100081， China;2.College of Information Engineering， Capital Normal University， Beijing 100048， China)

A validation method of experiment data abnormality was studied for the projectile impacting target plate experiment in this paper. It took a ballistic limit velocity calculation model based the dimensional analysis, and a calculation model fitted from experiment data. According to statistics theory, the validation method of ballistic limit velocity experiment data was proposed to estimate the possibility that confidence interval of standardized residual falls into standard normal distribution at specific confidence level. In addition, 12 ballistic limit velocity experiment data was obtained with the experiments that 6 kinds of mass (3.0, 4.5, 6.0, 7.5, 9.0 and 10.0 g total) of 35CrMnSi steel FSP projectile was used to impact typical high strength low alloy (HSLA) steel plates in 4 mm and 5 mm thickness, and the corresponding ballistic limit velocity calculation model was obtained with dimensional analysis and the experiment data. Based on the results that the standardized residual falls into (-1.96, 1.96) confidence interval at 95% confidence level, the ballistic limit velocity calculation model was validated and revised. The results show that the proposed method can be used to validate the abnormality of the ballistic limit velocity experiment data.

terminal effect; mathematical statistics;ballistic limitvelocity; residual

2015-11-15

国家自然科学基金资助项目(11402027)；北京理工大学基础科研基金资助项目(20130242005)

赵晓旭(1977—)，女，讲师，博士生，E-mail:zxx_nwj@sina.com.

徐豫新(1982—)，男，讲师，硕士生导师，E-mail:xuyuxin@bit.edu.cn.

TJ 012.4

A

1001-0645(2016)02-0144-04

10.15918/j.tbit1001-0645.2016.02.007