内部爆炸作用下混凝土靶背面临界震塌条件

段卓平， 张海英，2， 申健， 欧卓成， 黄风雷

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；2.中国核电工程有限公司 系统与布置设计所， 北京 100840；3.中华人民共和国国家知识产权局专利局 专利审查协作北京中心， 北京 100083)



内部爆炸作用下混凝土靶背面临界震塌条件

段卓平1， 张海英1，2， 申健3， 欧卓成1， 黄风雷1

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；2.中国核电工程有限公司 系统与布置设计所， 北京 100840；3.中华人民共和国国家知识产权局专利局 专利审查协作北京中心， 北京 100083)

为研究内部爆炸作用下混凝土靶背面临界震塌条件，采用量纲分析对内部爆炸作用下有限厚混凝土靶背面震塌破坏进行研究，得到了量纲一的临界震塌厚度的工程计算式. 结果表明，当装药密度一定时，随着装药直径或装药长径比的增加，临界震塌厚度也非线性递增，且存在极限临界震塌厚度；研究表明，临界震塌厚度关于装药直径存在第二类自相似.

爆炸；混凝土；震塌；装药长径比；装药直径

爆炸冲击载荷作用下，应力波传播至结构自由表面，产生强拉伸波，造成表面震塌和层裂，形成大量碎块. 碎块速度可高达每秒几十米甚至上千米，具有很大的杀伤和破坏威力，对结构内部人员和设备的安全威胁很大. Wu Chengqing等[1]试验研究了空气中爆炸载荷作用下混凝土靶背面层裂，得到了块体抛掷速度的经验公式. Ohkubo K等[2]试验研究了接触爆炸载荷作用下混凝土靶背面层裂和震塌贯穿时混凝土靶厚度与装药量之间的关系. Andras Schenker 等[3]、Wu C 等[4]和Yi Na-Hyun等[5]研究了爆炸载荷作用下不同强度的混凝土靶背面的动态力学参数的变化. 装药在结构物周围介质中或接触爆炸，采用小长径比或球形装药，通常采用球形装药近似理论，不考虑装药几何形状对爆炸破坏效应的影响.

随着科学技术发展，武器内部装药长径比越来越大，最大值可达10，当长径比达到6～8以上时，球形装药近似理论已不适用[6]. 内部爆炸作用下混凝土靶背面震塌效应及装药几何形状对爆炸破坏效应的影响的研究较少[7-9]，本文采用量纲分析法研究内部爆炸载荷作用下装药对混凝土靶背面震塌效应的影响，得到混凝土靶背面临界震塌厚度与装药之间的关系.

1 分析模型及假设

混凝土靶的厚度H一定，试验前采用相应直径的钻头在混凝土靶中心垂直向里钻成深度为h的预制孔，如图1所示. 当混凝土靶的震塌厚度R和装药直径D已知时，调整装药量m或装药长度L，得到混凝土靶背面临界震塌时的装药情况. 混凝土靶背面的震塌破坏随着装药量或装药长径的变化而发生变化. 当装药长径比较小时，只在混凝土靶背面出现辐射状裂纹；增加装药长径比，裂纹数量增加、宽度增大，甚至发生层裂，形成层裂坑，如图2(a)所示. 当装药长径比足够大时，震塌漏斗坑底部与装药预制孔发生贯穿，即临界震塌，如图2(b)所示. 装药长径比再增加时，震塌漏斗坑的深度将大于临界震塌厚度，如图2(c)所示. 因此，临界震塌状态时，混凝土靶背面的临界震塌厚度Rc等于预制孔方向上的剩余厚度，即混凝土靶背面震塌漏斗坑与应力波在介质中的传播、应力波在自由面上反射与爆生气体的膨胀等相关，为使问题清晰明了，做如下假设：

① 混凝土是各向同性的均匀介质，爆炸载荷作用下其内部应力分布与介质力学特性相关；

② 反射纵波的能量远大于反射横波的能量，只考虑纵波在混凝土中的传播规律；

③ 爆生气体与混凝土接触面上的压力均匀分布，爆生气体膨胀遵循多方指数气体状态方程；

④ 当参数或量纲一的变量趋近于0或无穷时，如果函数趋近于一个非零有限值，则与该量纲一变量对应的参数可以忽略不计[10]. 根据实际的物理现象，当装药埋深趋于无穷大时，临界震塌厚度将趋于一个非零有限值，故装药埋深对临界震塌厚度的影响可以忽略.

(1)

2 量纲分析

装药在岩石中爆炸时，岩石中的应力分布不仅与装药几何形状有关，还与装药与岩石之间的接触相关[6]. 由球形装药的爆炸规律知，当装药直径小于某一特征值时，爆轰波能量传递只与装药量和装药密度之比的3次方根成反比，满足相似律；否则，爆轰波传递能量与装药几何形状有关. 因此，引入装药稳定爆轰时的极限装药直径Dlimit作为特征量，TNT的极限装药直径Dlimit=5 mm[11-12]，混凝土与装药的相关参数如表1和表2中所示.

表1 装药的物理性质相关参数

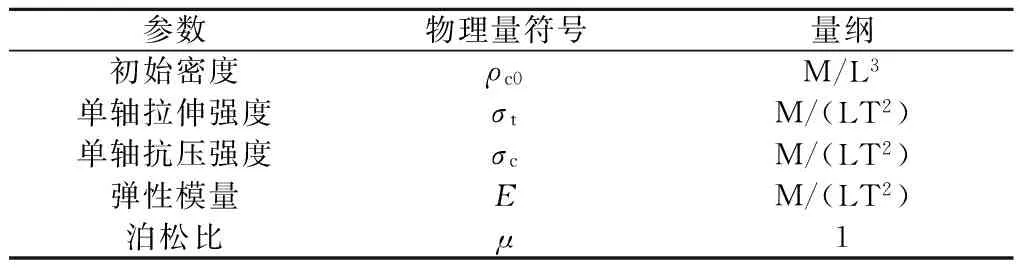
表 2 混凝土的物理性质相关参数

当装药TNT的密度ρe不变时，考虑装药直径D和装药长度L，则装药量M不再是一个独立的物理量.

(2)

内部爆炸载荷下混凝土靶背面的临界震塌厚度Rc可表示为

(3)

根据BuckinghamΠ定理，式(3)可以表示成量纲一的形式

(4)

其中

当混凝土配合比、材料密度等都不发生变化时，量纲一的量Π3，Π4，…，Π9均为常数，临界震塌厚度是装药长径比和量纲一的装药直径的函数.

(5)

内部爆炸载荷作用下有限厚混凝土靶背面的临界震塌厚度不仅与装药直径有关，还与装药长径比有关.

3 第二类自相似

当量纲分析得到的相似变量Πi趋近于0或无穷，函数F不存在非零有限极限，且关于Πi有近似幂定律(缩比)形式，则函数关于该相似变量存在第二类自相似[10].

随着装药直径和装药长径比的变化，临界震塌厚度的变化如图3和图4所示，当量纲一的装药直径Dlimit/D趋近于0时，即装药直径D趋近于无穷大，量纲一的临界震塌厚度Rc/D是非线性递增；当量纲一的装药直径Dlimit/D趋近于无穷大时，即装药直径D趋近于0，量纲一的临界震塌厚度Rc/D递减并将趋于0. 因此，当量纲一的装药直径Dlimit/D趋近于0或无穷时，式(5)中函数F不存在非零有限极限.

假设内部爆炸载荷作用下混凝土靶背面的临界震塌厚度与装药直径满足幂函数形式，式(5)可以写成

(6)

从图3和图4可以得出，量纲一的临界震塌厚度分别随量纲一的装药直径和装药长径比的变化而变化. 式(6)中的f函数是单调递增函数，且应该存在一个非零极限值. 从物理现象的实际意义出发，当装药长径比为0时，临界震塌厚度必为0，故临界震塌厚度与装药长径比之间的曲线经过点(0，0)，函数f可拟合为

(7)

式中(Rc/D)/(Dlimit/D)-0.65为量纲一的临界震塌厚度的另一种表达形式，其极限值为4.68. 式(7)的有效范围为0

临界震塌厚度与装药直径的幂函数形式的假设是成立的，根据第二类相似解的定义[10]，临界震塌厚度关于装药直径存在第二类自相似现象.

4 结 论

本文采用量纲分析法对内部爆炸作用下的有限厚混凝土靶背面震塌破坏进行分析. 研究表明，混凝土靶背面临界震塌厚度不仅与装药长径比有关，还与装药直径有关，且临界震塌厚度关于装药直径存在第二类自相似现象. 通过量纲分析还得到了量纲一的临界震塌厚度的工程计算式，当装药密度一定时，随着装药直径或装药长径比的增加，且存在极限临界震塌厚度.

[1] Wu C Q， Ratni N， John O D. Fragmentation from spallation of RC slabs due to airblast loads[J]. International Journal of Impact Engineering， 2009，36:1371-1376．

[2] Ohkubo K， Beppu M， Ohno T， et al. Experimental study on the effectiveness of fiber sheet reinforcement on the explosive-resistant performance of concrete plates[J]. International Journal of Impact Engineering， 2008，35:1702-1708．

[3] Schenker A， Anteby I， Gal E， et al. Full-scale field tests of concrete slabs subjected to blast loads[J]. International Journal of Impact Engineering， 2008，35:184-198．

[4] Wu C， Oehlers D J， Rebentrost M， et al. Blast testing of ultra-high performance fibre and FRP retrofitted concrete slabs[J]. Engineering Structures， 2009，31:2060-2069．

[5] Yi N H， Kim J H J， Han T S， et al. Blast-resistant characteristics of ultra-high strength concrete and reactive powder concrete[J]. Construction and Building Materials， 2012，28(1):694-707．

[6] 王仲琦，张奇，白春华.孔深影响爆炸应力波特性的数值分析[J].岩石力学与工程学报，2002，21(4):550-553．

Wang Zhongqi， Zhang Qi， Bai Chunhua. Numerical simulation on influence of hole depth on explosion effect [J]. Chinese Journal of Rock Mechanics and Engineering， 2002，21(4):550-553. (in Chinese)

[7] Barenblatt G I. Scaling， self-similarity and intermediate asymptotics[M]. New York: Cambridge University Press，1996．

[8] Haas C H， Rinehart J S. Coupling between unconfined cylindrical explosive charges and rock[J]. Int J Rock Mech Mining Sci， 1965，2(1):13-24．

[9] 刘彦，段卓平，王新生，等.不同厚度壳体装药在混凝土中爆炸的实验研究[J].北京理工大学学报，2010，30(7)：771-774.

Liu Yan, Duan Zhuoping, Wang Xinsheng, et al. Experiments on explosion of explosives with different thickness shells in concretes[J]. Transactions of Beijing Institute of Technology, 2010,30(7):771-774. (in Chinese)

[10] Meyers M A. Dynamic behavior of materials [M]. [S.l.]:Wiley， 1994．

[11] 张海英，段卓平，刘彦，等.混凝土内部爆炸震塌临界破坏试验研究[J].兵工学报，2011，32(2):310-314．

Zhang Haiying， Duan Zhuoping， Liu Yan， et al. Experimental study on critical collapseof concrete targets subjected to internal explosion [J]. Acta Armament-arii， 2011，32(2):310-314. (in Chinese)

[12] 张海英，段卓平，刘彦，等.有限厚混凝土靶内部爆炸震塌贯穿研究[J].北京理工大学学报，2013，33(5):441-444．

Zhang Haiying， Duan Zhuoping， Liu Yan， et al. Study on the collapse perforation of thick concrete targets under internal explosion[J]. Transactions of Beijing Institute of Technology， 2013，33(5):441-444. (in Chinese)

(责任编辑：刘雨)

Critical Collapse at Rear Surface of Concrete Targets Under Internal Explosion

DUAN Zhuo-ping1， ZHANG Hai-ying1，2， SHEN Jian3， OU Zhuo-cheng1， HUANG Feng-lei1

(1.State Key Laboratory of Explosive Science and Technology， Beijing Institute of Technology， Beijing 100081， China；2.China Nuclear Power Engneering Co. Ltd., Process and Layout Design Division， Beijing 100840， China；3.Patent Examination Cooperation Center of the Patent Office， State Intellectual Property Office of the People Republic of China， Beijing 100083， China)

To study critical collapse at rear surface of concrete targets under internal explosion, the collapse on the rear surface of concrete targets with finite thickness under internal explosion was studied, and the engineering formula of the dimensionless critical collapse thickness was obtained. The result shows that, when the density of charge is fixed, the critical collapse thickness increases non-linearly with the increase of the diameter or the length-to-diameter ratio of charge, and has a limit value. In addition, it is found that there exists the second kind of similarity of the critical collapse thickness in the diameter of charge.

explosion; concrete; collapse; length-to-diameter ratio of charge; diameter of charge

2014-03-07

国家自然科学基金资助项目(11221202)

段卓平(1965—)，男，教授，博士生导师，E-mail：duanzp@bit.edu.cn.

张海英(1983—)，女，博士，E-mail：zhy1322@bit.edu.cn.

O 383

A

1001-0645(2016)02-0133-04

10.15918/j.tbit1001-0645.2016.02.005