高价值弹药引信发射环境模拟的多变量优化*
乔 宇,李 波,李培英,张 亚,李世中
(1 中北大学机电工程学院,太原 030051;2 邯郸学院,河北邯郸 056005)
0 引言
由于高价值弹药引信测试试射成本高昂,为了降低成本,尝试采用常规弹丸模拟引信发射环境的方案。在模拟试验之前,需要针对高价值弹药的发射环境,建立最优算法进行数值仿真分析。
针对调整弹丸初速问题,有通过保持发射药装药量、初始容积等弹药结构参数不变,增加泄气孔的方式实现初速改变[1],但是改变了身管结构,需重新设计身管,对节省成本不利。也有采用传统火炮发射与火箭喷射原理相结合的组合发射工作模式,为弹丸加载固体随行装药来提高初速,维持或降低膛压[2-5],但需对弹丸进行结构设计,不利于普及。
在发射数值模拟研究中既可使用基于任意拉格朗日欧拉方法的二维气-固两相流算法[6],也可采用随机模拟来确定满足发射性能指标的装药量、药厚和火药力的散布区间从而建立数学算法[7-8],还可利用MATLAB编写程序来模拟发射环境[9-10],以研究装填诸元对发射环境的影响。但以上方法都只研究了单一变量对于发射环境的影响,并未针对多变量同时作用下的发射环境变化进行深入探讨。
文中在仿真过程中发现,装药量或弹丸质量的单独改变并不是最优选择。采用多自变量输入来观察在出炮口速度、膛内后坐过载都符合理想要求的情况下,寻找使膛压达到最低值的装药量和弹丸质量匹配组数据,以达到在低膛压完成要求指标的目的。该方法无需对模拟装置身管或者弹丸进行结构再设计,节省人力物力,利于实施。
1 发射环境算法建立
根据经典内弹道学理论,发射方程组是基于以下基本假设:
1)火药燃烧遵循几何燃烧定律;
2)药粒均在平均压力下燃烧,且遵循燃烧速度定律;
3)内膛表面热散失用减小火药力f或增加比热比k的方法间接修正;
4)用系数φ来考虑其他的次要功;
5)弹带挤进膛线是瞬时完成的,以一定的挤进压力p0标志弹丸的启动条件;
6)火药燃气服从诺贝尔-阿贝尔状态方程;
7)单位质量火药燃烧所放出的热量及生成的燃气的燃烧温度均为定值,在以后膨胀做功过程中,不考虑燃气组分的变化,因此虽然燃气温度因膨胀而下降,但火药力f、余容α及比热比k等均视为常数;
8)弹带挤入膛线后,密闭良好,不存在漏气现象。
经典内弹道单一装药方程组为:
(1)
式中:
(2)
p是弹后平均压力;v是弹丸速度;l是弹丸行程;t是弹丸在膛内的运动时间;ψ是火药相对燃烧质量;lψ是药室自由容积缩颈长;l0是药室容积缩颈长;f是火药力;Δ是装填密度;α是余容;u1是燃速常数;ρp是火药的密度;Z是已燃相对厚度;S是炮腔横截面积;ω是装药量;m是弹丸质量。

(3)
(4)
于是燃烧速度定律和弹丸运动方程变为:
(5)
(6)
其中
(7)
综上,以相对量表示的内弹道方程组为:
(8)
式中:
(9)
式中:
(10)
2 数值模拟算法的建立
根据相对量表示的内弹道方程组编写MATLAB程序,计算在给定装填诸元情况下的p-t和v-t曲线图如图1、图2所示。

图1 给定装填条件下p-t曲线图

图2 给定装填条件下v-t曲线图
由图1~图2可得弹底压力p和弹丸速度v与弹丸在膛内运动时间t的关系。为了使模拟的引信发射环境与高价值弹药引信的真实发射环境相一致,需要修改发射装填诸元。文中主要讨论装药量ω、弹丸质量m改变对发射环境的影响。
2.1 单一变量算法
首先讨论ω在一定范围内其变化对发射环境的影响。
1)装药量ω对发射环境的影响

图3 ω变化时pmax-ω曲线图

图4 ω变化时vz-ω曲线图
由图3~图4得到发射环境弹底最大压力pmax与装药量ω成二次幂关系,弹丸出炮口速度vz与装药量ω成正比例关系。即发射环境中以上4种环境与装药量ω成正增益的关系,各环境随着装药量ω的增加而增加。
对于模拟装置身管,平均压力增大是不良增益,会导致身管寿命减小,严重者导致在发射过程中发生炸膛等危险情况;对于弹丸,后坐过载增大是不良增益,会导致弹丸内部引信部件无法承受过载,使引信失效,发生哑火甚至过早解除保险等危险情况。
2)弹丸质量m对发射环境的影响
由图5~图6得发射环境弹底最大压力pmax与弹丸质量m成正比例关系,弹丸出炮口速度vz与弹丸质量m成反比例关系。即弹丸质量的增加对于身管和弹丸内部引信结构而言是良性增益,能够减少身管和引信的负载;对弹丸的出炮口速度和转速属于不良增益,会导致其出炮口速度和转速下降。
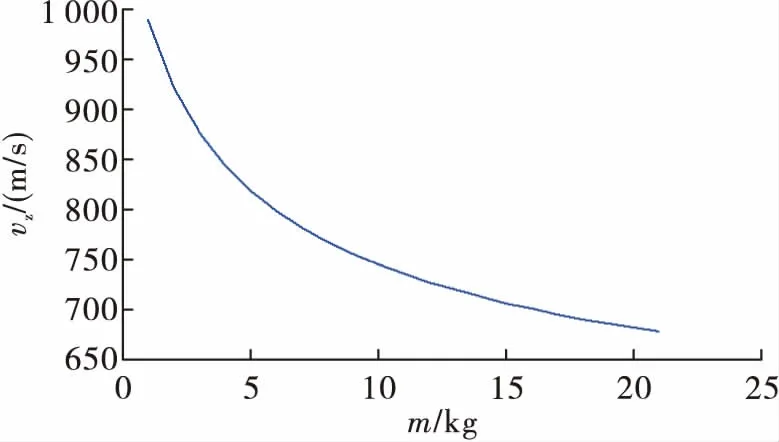
图6 m变化时vz-m曲线图
可见单一自变量对于发射环境的影响均为单向,不能在提高初速的同时保持膛内弹底压力变化浮动较小或不变,亦不能在减小弹底压力的同时增加初速,需建立多变量算法来同时满足以上两种情况。
由于弹丸质量的减少,必然带来外弹道环境的改变,文中目前主要针对发射环境讨论,外弹道不属于讨论范围。
2.2 双变量算法
该算法主要针对装药量ω和弹丸质量m各自改变时,对发射环境中弹底最大压力pmax和出炮口速度vz的影响。
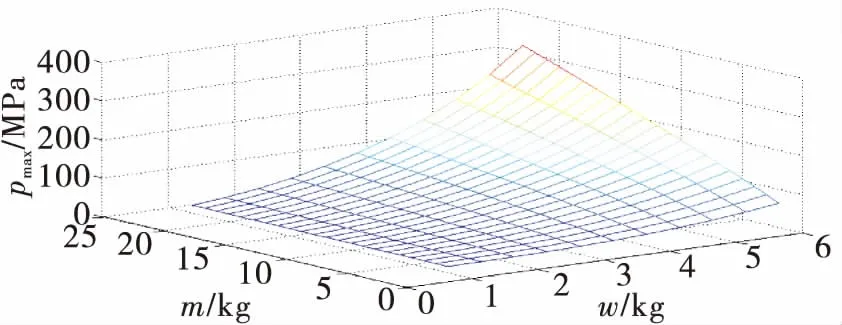
图7 ω、m变化时pmax-ω、m曲线图
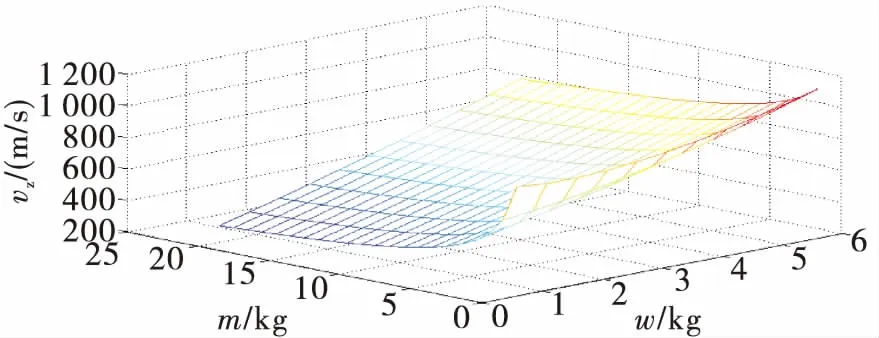
图8 ω、m变化时vmax-ω、m曲线图
由图7~图8可知,装药量ω和弹丸质量m对出炮口速度vz的影响随其两者变化方向的不同而改变。对于弹底最大压力pmax,两者同时增大时pmax也会增大。则装药量和弹丸质量不能同时朝向增加的趋势变化,必要有一者朝向减少的趋势变化,维持pmax不变或获得小幅增加。
3 最优解的获得
针对模拟高价值弹药引信发射环境的工作状态,需从多变量算法中选取能完成模拟试验且最大限度保护模拟装置和引信的装药量ω和弹丸质量m。由于算法计算取值只能取到经过其计算的值,所以装药量ω和弹丸质量m的取值步长越小越能计算出准确的数据。
对弹底最大压力pmax和出炮口速度vz的取值需在其附近范围,以囊括满足条件的装药量ω和弹丸质量m的取值。
选取最优解过程如下:
1)确定身管能承受的最大安全膛压,取小于其值20 MPa的范围;
2)用该取值范围与弹底最大压力pmax-ω、m曲线图相交,可得在安全膛压取值范围内装药量ω和弹丸质量m对应取值情况,如图9;
3)在求解符合炮口速度vz要求的装药量ω和弹丸质量m时,根据要求的炮口速度,重复步骤1)和2),其中将pmax-ω、m曲线图更换为vz-ω、m曲线图,得图10;
4)选择图9、图10相交点或邻近点,得满足安全膛压和出炮口速度要求的装药量ω和弹丸质量m,得最优解。

图9 满足安全膛压要求的ω和m平面相交图
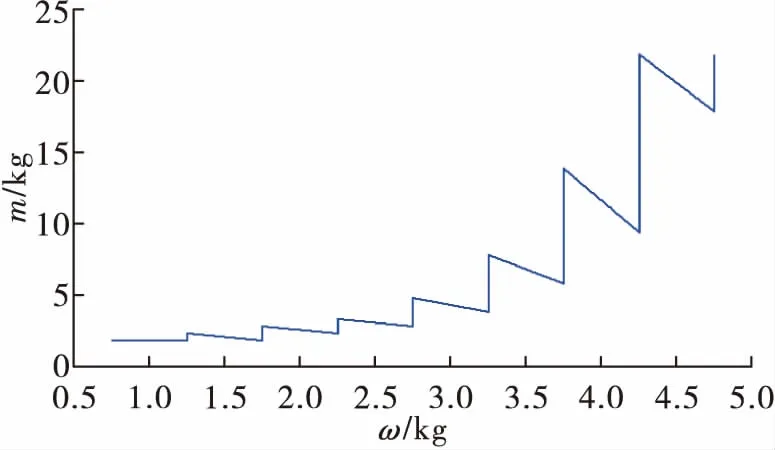
图10 满足初速要求的ω和m平面相交图
图9和图10相交于ω=4.759 kg和弹丸质量m为19.76~21.76 kg,该范围内均能满足安全膛压和出炮口速度的要求。
对于最大安全膛压在220 MPa,出炮口速度达到600~700 m/s的引信,宜选取装药量为4.759 kg,弹丸质量为19.76~21.76 kg的匹配组数据,进行对于高价值弹药引信发射环境模拟试验。
该最优解的发射环境变化如图11~图12。
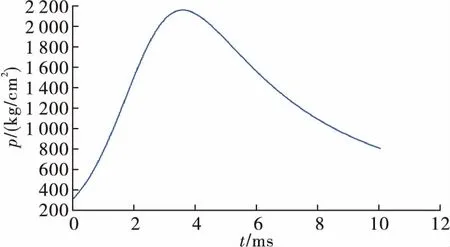
图11 满足要求的p-t曲线图

图12 满足要求的v-t曲线
从图11、图12可知该最优解的发射环境曲线都较理想,能够完成安全膛压为220 MPa,出炮口速度达到600~700 m/s的高价值弹药引信在发射环境中的模拟试验,对高价值弹药引信的研发有积极作用。
4 结论
文中所研究的高价值弹药引信发射环境模拟的多自变量算法,从实际出发,为了减少参数选择困难,通过算法构建,能够找到符合要求且使得模拟装置身管有更长使用寿命的最优解,对高价值弹药引信模拟试验的优化有指导作用,对大幅减少高价值弹药引信的研发成本有重大意义。该算法亦可以改变自变量,以研究多因素变化时发射环境的改变,选择最优解。

