空间目标碰撞预警摄动因素研究

荣吉利， 谌相宇， 齐跃

(1.北京理工大学 宇航学院， 北京 100081； 2.北京空间飞行器总体设计部， 北京 100094)



空间目标碰撞预警摄动因素研究

荣吉利1， 谌相宇1， 齐跃2

(1.北京理工大学 宇航学院， 北京 100081； 2.北京空间飞行器总体设计部， 北京 100094)

针对解析筛选方法中摄动因素易造成漏报危险时间区间的问题，改进了时间筛选算法. 该方法在时间筛选中，增加了初始窗口修正，并在周期修正中考虑了偏心率摄动. 以2005年发生的空间目标相撞事件为例，在不同的预警时间区间中，讨论了摄动因素对几何筛选的影响，并对比了无摄动、原方法和改进的时间筛选方法得到的危险时间区间. 结果表明，摄动因素可有效降低几何筛选中由接近距离偏小造成错误筛除危险目标的风险，改进后的时间筛选算法比原方法能得到更为完整准确的危险时间区间.

空间目标；碰撞预警；轨道筛选；摄动

近年来，随着人类空间活动的日益增多，产生了大量的空间碎片. 据美国空间监视网SSN公布的数据，截至2014年1月，直径大于10 cm的在轨空间目标已超过16 000个. 空间环境的日益恶化，对在轨航天器的安全构成了严重威胁. 为了提高航天器运行寿命、降低航天器失效风险，必须对航天器进行碰撞预警.

碰撞预警技术主要包括：编目数据获取、轨道实时更新、危险目标筛选、碰撞风险评估等. 采用北美防空联合司令部(NORAD)每日更新的两行根数(TLEs)，通过与两行根数配套的SGP4/SDP4轨道预报模型[1-2]，可对空间目标的轨道根数进行更新. 危险目标的筛选主要分为两大类：一种是解析方法，由Hoots于1984年提出[3]，该方法通过高度筛选、几何筛选、时间筛选来确定空间目标与危险目标的接近区间，是应用较早、较成熟的算法；一种是数值方法，主要包括A-N算法[4]和运动学筛选算法[5]，通过插值、拟合、多项式求根等数值方法获得目标的交会信息. 数值方法计算时间长，不便于长时间的快速预警，而解析方法不仅计算速度快，并且物理意义明确，可获得碰撞点的变化规律，为机动规避方法的选择奠定基础，但存在由摄动造成漏报的风险[6]. 通过危险目标筛选，可剔除掉大部分与航天器不相交的空间目标，对剩余的目标进行碰撞风险评估，即可判别航天器的在轨安全.

目前，国内解析筛选方法研究多针对筛选效率[7-8]，较少研究摄动因素对筛选结果的准确性的影响. 本文以文献[3]的方法为基础，研究摄动因素对几何筛选与时间筛选的影响，并对时间筛选进行改进，通过参照2005年发生的空间目标碰撞事件，验证摄动因素的重要性.

1 筛选方法

从编目数据中筛选出危险目标，即在预警时间区间[tB，tE]内，按照一定的判断标准(接近距离D)，剔除掉不会与航天器(主目标P)交会的待筛选目标(从目标S)，从而得到危险目标的编号和接近时刻.

1.1 高度筛选

对于主目标和从目标，令q等于两目标近地点高度中的较大值，Q等于两目标远地点高度中的较小值，如果满足q-Q>D，则可剔除掉该从目标.

1.2 几何筛选

对于未被高度筛选剔除的目标，通过对两目标轨道的几何位置进行分析，得到轨道交线附近的两个接近点及其接近距离d1和d2，如果d1和d2均大于D，即可剔除掉该从目标. 具体公式可参看文献[3].

1.3 时间筛选

对于剩余的目标，利用空间目标到另一目标的垂直距离z*=rsinIRsinuR可解析估计两目标在飞过轨道交线附近的危险时间段，其中IR相对轨道倾角，uR=f+w-Δ为真近点角f、近地点幅角w、轨道升交点与交线夹角Δ的函数.

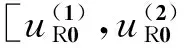
2 摄动因素

以上所给出的分析均在二体轨道下给出的. 在实际太空环境中，空间目标受到多种摄动因素的作用，在长期摄动项的作用下空间目标会逐渐偏离二体轨道，仅在二体意义下讨论危险目标的筛选存在漏报的风险. 考虑摄动因素的轨道根数表达式为[3]

(1)

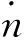
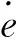
(2)

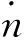
2.1 几何筛选

考虑摄动项的最近距离rrel为

(3)

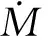
2.2 时间筛选

角度窗口的计算公式为

(4)

式中f=uR-(ω-Δ). 在摄动条件下，式(4)中的变量为a，e，IR，uR及ω-Δ，将式(4)变形为

(5)

对式(5)关于a，e，IR，uR及ω-Δ求偏导得

(6)

其中Fi(i=a，e，IR，ω-Δ，uR)表示式(5)对各变量的偏导，由于篇幅有限在此不再一一列出. 由式(6)得到

(7)

(8)

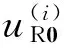
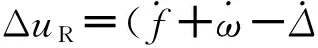
T=

(9)

文献[3]中修正后的角度窗口周期为

(10)

3 数值算例

以2005年1月发生的空间目标相撞事件为例，通过对比是否考虑摄动因素得到的最近距离及危险时间区间，验证摄动因素在碰撞预警中的重要性；通过对比文献[3]及本文提出的改进方法得到的危险时间区间，验证改进方法的有效性.

两空间目标分别为：编号07219的美国火箭残骸及编号26207的长征火箭第三级碎片. 两目标的交会时刻为2005年1月17日02:14:37，其最大碰撞概率超过10-3，达到红色预警门限[9]. 取两目标于碰撞前0.5 d的TLEs数据，如表1所示.

表1 两目标两行根数TLEs

在整个筛选过程中，两目标的轨道根数均由SGP4模型进行更新，该模型的计算精度及准确性已得到验证[10].

3.1 几何筛选

表2 摄动因素对最近距离的影响

Tab.2 Influence of perturbation factors on the relative minimum distance

时间rrel,tmid/kmrrel,min/km(Δr/rrel,tmid)/%6∶16∶33.68.917.1919.36∶36∶43.27.946.1822.17∶57∶14.410.58.8316.0

3.2 时间筛选

与几何筛选类似，设时间区间[tB，tE]的长度固定为24 h，时间区间的中点时刻tmid分别为16日21时、22时、23时及17日0时，得到4个筛选区间. 分别采用无摄动、文献[3]及本文提出的方法计算4个时间区间内的危险区间，列于表3.

如表3所示，在4个筛选区间内，均存在2个危险时间区间. 不考虑摄动的方法在tmid距实际交会时刻较远的16日21时及16日22时漏报实际交会时刻2∶14∶37所对应的区间，因此无摄动的方法不适用于tmid距实际交会时刻较远的情况. 文献[3]的方法较无摄动方法有一定的改进，但同样在16日21时漏报实际交会时刻所对应的区间，而本文给出的改进方法在4个筛选区间内均能得到交会区间. 改进后的方法在tmid距交会时刻较远时，仍能得到交会时刻对应的区间，与前两种方法相比具有更好的稳定性. 随着tmid靠近实际交会时刻，3种筛选方法均不存在漏报危险区间的情况，得到的危险时间区间也逐步向交会时刻靠近，但由本文方法得到的危险时间区间较无摄动方法更接近实际的交会时刻.

表3 时间筛选结果

4 结 论

研究表明，预警时间区间的不同对几何筛选和时间筛选影响较大，得到的筛选结果随中点时刻而变化. 考虑摄动因素后，在几何筛选中，可有效降低由于接近距离设置偏小而错误筛除危险目标的风险；在时间筛选中，可较无摄动方法得到更为完整、准确的危险时间区间. 改进后的时间筛选算法，可在预警时间区间中点时刻距离交会时刻较远时，仍能得到完整的危险时间区间，提高了筛选的准确性，具有更强的稳定性.

[1] Hoots F R， Roehrich R L. Models for propagation of nORAD element sets[R]. [S.l.]: Space Track Report， 1980.

[2] Vallado D A， Crawford P， Hujsak R， et al. Revisiting spacetrack report#3[R]. [S.l.]: AIAA， 2006-6753．

[3] Hoots F R， Linda L. An analytic method to determine future close approaches between satellites[J]. Celestial Mechanics， 1984，33:143-158．

[4] Alfano S， Negron D. Determining satellite close approach[J]. Journal of the Astronautical Sciences， 1993，41(2):217-225．

[5] Alarcon-Rodriguez J R， Martinez-Fadrique F M， Klinkrad H. Collision risk assessment with a smart sieve method[C]∥Proceedings of Joint ESA/NASA Space-Flight Safety Conferense. Noordwijk， Nether-lands: [s.n.]， 2002．

[6] 白显宗，陈磊，张翼，等.空间目标碰撞预警技术研究综述[J].宇航学报，2013，34(8):1027-1039．

Bai Xianzong， Chen Lei， Zhang Yi， et al. Survey on collision assessment and warning techniques for space orbit[J]. Journal of Astronautics， 2013，34(8):1027-1039.(in Chinese)

[7] 杨志涛，刘林，刘静，等.空间目标碰撞预警中的一种高效筛选方法[J].空间科学学报， 2013，33(2):176-181．

Yang Zhitao， Liu Lin， Liu Jing， et al. A high efficiency orbit screening method for space debris collision prediction[J]. Chinese Journal of Space Science， 2013， 33(2):176-181. (in Chinese)

[8] 郑勤余，吴连大.卫星与空间碎片碰撞预警的快速算法[J].天文学报，2004，45(4): 422-427．

Zheng Qinyu， Wu Lianda. A computation method to warn the collision prediction research[J]. Acta Astronomica Sinica， 2004，45(4):422-427.(in Chinese)

[9] 白显宗，陈磊.空间目标碰撞概率计算方法研究[J].宇航学报，2008，29(4):1435-1442．

Bai Xianzong， Chen Lei. Research on calculational method of collision probability between space objects[J]. Journal of Astronautics， 2008，29(4):1435-1442. (in Chinese)

[10] 荣吉利，齐跃，谌相宇.SGP4模型用于空间目标碰撞预警的准确性与有效性分析[J].北京理工大学学报，2013，33(12):1309-1312．

Rong Jili， Qi Yue， Chen Xiangyu. Accuracy and effectiveness analysis of SGP4 implemented in space debris collision alert[J].Transactions of Beijing Institute of Technology， 2013，33(12):1309-1312. (in Chinese)

(责任编辑：刘雨)

The Perturbation Effects on the Collision Warning for Space Object

RONG Ji-li1， CHEN Xiang-yu1， QI Yue2

(1.School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China;2.Beijing Institute of Spacecraft System Engineering， Beijing 100094， China)

For the problem of omitting dangerous time windows caused by perturbation factors while using analytical methods, the time prefilter algorithm was improved. In this method, the perturbation effect on first time window correction was introduced, and the effect of oblateness on the period of time window was considered. Take the space collision between two space objects in 2005 as an example, the perturbation effect on geometrical prefilter in the different time spans of interest was discussed, and the time windows that were calculated respectively by the time prefilter with no perturbation method, original method and improved method were compared. Results show that perturbation factor consideration can effectively reduce the risks of error screening dangerous targets due to chosen too small approach distance, and the time windows got from improved time prefilter algorithm is more complete and accurate.

space object; collision warning; orbit screening; perturbation

2014-10-07

国家部委预研项目(KJSP2006-0106)

荣吉利(1964—)，男，博士，教授，E-mail:Rongjili@bit.edu.cn.

V 528

A

1001-0645(2016)02-0128-05

10.15918/j.tbit1001-0645.2016.02.004