横向联系，纵向延伸——例谈数学学习中的知识点化和拓展

江苏省海门市能仁中学 花永平

横向联系，纵向延伸
——例谈数学学习中的知识点化和拓展

江苏省海门市能仁中学 花永平

数学的学习不是单一、独立的个体，从数学方面来分析，数学每个知识与技能之间都是精密联系、融会贯通、相辅相成的。从学术上面分析，数学和其他学科之间又是相辅相成的。本文结合教学实践，谈谈如何在教学实践中注重数学学科间的联系，达成横向联系，纵向延伸的效果，最终促使学生学习效率的提升，学习能力的提升。

横向；纵向；联系；延伸

数学学科作为一门基础学科，虽然由很多微小的知识点构成，但是知识点不是孤立的，它们之间有关联，有类比，有拓展，有延伸。

一、教学小片段

1.人教版七年级上册中线段中点定义和推理教学。

把纸条对折，找出它的中点。（操作层面）

若线段上的一点将线段平均分为两份，这样的点叫作线段的中点。（文字语言）

若M为线段AB上的点，且AM=BM，则点M为线段AB的中点。即因为点M是线段AB的中点，所以。（符号语言）

2.定义本质：揭示了位置和数量关系的相互转化。

3.基本应用：母题：如图1，点M为线段AB的中点，AB=8，求AM的长。

教学设计：要求学生掌握一步推理：

4.变式一：如图 2点C为线段AB上的任意一点，M为AB的中点，N为BC的中点。AB=8，求MN的长。

变式二：接变式一，如果点C为直线AB上的任意一点，M为AC的中点，N为BC中点。AB=8，求MN的长。分类讨论：点C在线段AB上或者在它的延长线上。

①C在线段AB上，如变式一。

二、横向联系

与线段等价的一个几何图形为角，与线段中点对应的是角的平分线，在数学学习中采用类化学习方式对角平分线的相关计算作出研究。

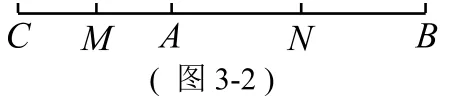
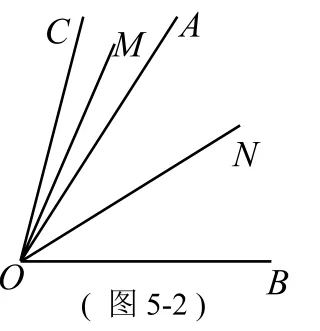
类似变式一，如图4：OC为∠AOB内部一射线，OM平分∠AOC，ON平分∠BOC，∠AOB=80°。求∠MON的度数。

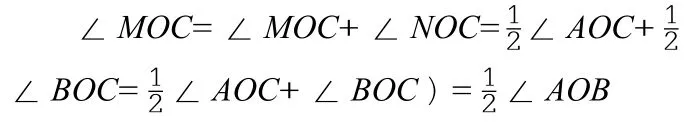
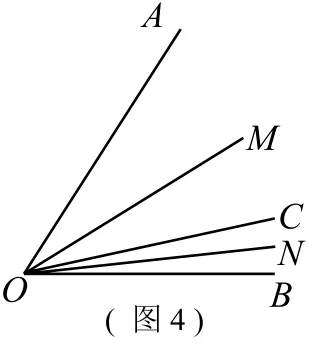
类似变式二，OC为形内（如图4），点OC在形外：

①当OC在OB的下方，如图5-1，

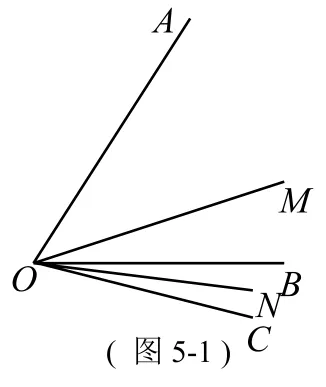
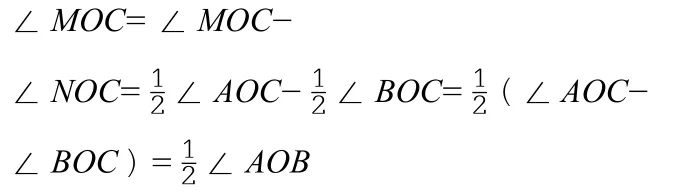
②当OC在OA的上方，如图5-2，

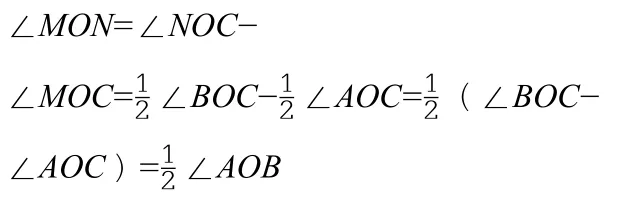
百密还有一疏，当∠BOC和∠AOC均为钝角时，结果会怎么样呢？如图5-3，∠MON=∠MOC+∠NOC

由此可以看出，它与线段中点既有统一的一面，也有互补的一面，所以在数学学习中，更应该关注在形的不同概念之间揭示的不同的数量关系。

三、纵向延伸

在线段双重中点的学习中我们发现，不论C点在线段AB上还是在延长线上，我们均有两中点之间的距离与原有线段的关系。即MN=AB.在数学学习中，就可以做出一个大胆的猜测，若点C不是直线上的任意一点呢，结论是否依然成立呢？

1.对学习思维的跳跃和呈现，很多同学有点惊讶，其实，教学本身就是不断发散和发展的过程，当点C为平面上的任意一点时，如图6，M、N为AB、AC的中点，我们发现，MN=AB，并且MN∥AB。于是又有了新的发现：不仅仅存在数量关系，而且和存在相应的位置有关系。（三角形中位线定理）2.如图7，若S为平面ABC外一点，M、N、P分别为SA，SB，SC的中点，不难发现：

（1）MN∥AB，MP∥AC，NP∥BC；

（2）平面PMN∥平面ABC；

（3）△MPN与△ABC关于点C成位似，且位似比为1：2；

（4）S△MPN=S△ABC。

四、拓展应用

摄影组从A市到B市有一天的路程，计划上午比下午多走100千米，到C市由于堵车中午才赶到了小镇，只行驶了计划的三分之一。过了小镇汽车赶了400千米，司机说再走从C市到这的二分之一就到达目的地了。AB两市相距几千米？

基本解析：可以用方程；也可以用推理。重点关注中点和数量关系。

总之，数学学习的本真在于总结和归纳，触类旁通，解决一类问题是学好数学的根本。一个知识点既要看到它的基本点，又要看到它的生长点，更要看到它的拓宽点，所以，数学学习就是从小世界去看待大问题，只有这样坚持不懈，才会得以学习的发展和提高。