课本，不仅是课本——有效挖掘课本习题的潜在功能

江苏省海门市海南中学 黄 华

课本，不仅是课本
——有效挖掘课本习题的潜在功能

江苏省海门市海南中学 黄 华

在当下的数学课堂中，我们发现很多教师喜欢脱离书本，架构适合自己需要的课堂教学的学习单或者学案。教师结合教材和学生变通教材固然是好，但是我们的出发点应该还是学生和教材本身，教师可以变通教材，但是不能脱离教材，教材内部其实还是有很多很多值得挖掘的素材和价值，就课本中那些看似简单的习题，就值得我们进行深入的分析和变通。

习题；本质；典型；错误；变化

课本是数学教学开展的基础和依据，但却不是初中数学的全部。特别是在面对课本当中的习题时，教师们需要从两个层面进行把握：首先，课本习题是数学教学开展的基础，其大多是从基本知识内容的角度出发来设计练习的，与教材内容贴合得十分紧密，对于夯实学生知识基础来讲起到了十分重要的稳固作用。另外，课本习题的作用也并不仅仅停留在表面状态上。只要耐心挖掘课本习题本质便会发现，它不仅对知识内容进行了强调，还彰显出了更为重要的思维方法，对于数学思想的提升也能够提供有力推动。因此，勤于对课本习题进行挖掘，对于初中数学的有效教学来讲意义重大。

一、总结习题本质，把握知识内容

每一道课本习题都不是随意出现的，它们都是基于教材当中的知识内容设计出来的。可以说，课本当中出现的习题是训练起来最对路子的。因此，想要迈出有效学习的第一步，应当从对课本习题的重点关注开始。当我们静下心来分析每一道课本习题时便会发现，每一个问题背后都隐藏着最原汁原味的知识内容，而这就是最应当予以掌握的部分。

例如，在学习过统计的相关知识内容后，我向学生们提出了这样一个问题：商场中正在销售某品牌的皮鞋，经过调查统计，发现各型号的皮鞋所对应的销售量如下表所示。商场的销售经理想要知道哪个型号的皮鞋销量最大，那么，他最应当关注哪一个统计量？在这个问题的思考中，学生们大多会在平均数、众数、中位数和方差几个答案中徘徊。对于这道习题，我带领学生对其中的考查内容进行了分析，大家发现，解答的重点在于对不同统计量基本概念的深入理解。这道题在不知不觉中为学生们的统计知识学习点明了关键之所在。

型号 22 22.5 23 23.5 24 24.5 25数量（双） 3 5 10 15 8 3 2

面对课本习题，解答问题不是关键，最重要的是抽丝剥茧地发现其本质，将每一个问题所强调的知识内容总结出来。学生们在学习过程当中总是抱怨知识点过于零碎，希望对其有一个明确的总结。实际上，我们并不需要刻意去总结什么，只要将教材中习题所突出的知识点掌握住，学习效果基本上就可以保证了。从这个角度来讲，课本习题完全可以发挥出课后二次教学的作用。

二、利用典型错误，弥补学习漏洞

课本习题往往会应用于课堂教学刚刚结束之后。这个时候，学生们对于新知识内容的理解还没有完全到位，仅靠教师在课堂上的初次教学，也很难做到毫无瑕疵地对知识予以掌握。因此，在对课本习题进行解答时，难免出现各种困难与错误。对于数学学习来讲，这些错误就是最宝贵的素材。如果教师们能够及时抓住这些错误当中的典型部分进行强调，将对知识教学助力不少。

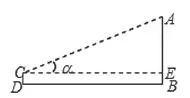
例如，在学习过三角形及三角函数的内容后，课后出现了这样一个应用性问题：如图所示，AB是一根电线杆，点D与它之间的距离是25米，为了测量电线杆的高度，某人利用一个高为1.2米的测角仪CD测得电线杆最高点A的仰角α为22°。由此可知，电线杆AB的高度是多少（sin22°=0.3746，cos22°=0.9272，tan22°=0.4040，cot22°=2.4751）？在这个问题的解答中，学生们的错误主要集中在两个地方：一是三角函数选择错误，二是没有将CD的高度考虑在内。由此，我向学生们巩固了不同三角函数的含义与记忆方法，并强调了审题中的细节关注。

通过分析学生们在解题过程当中出现的问题便不难发现，这些错误的分布往往是比较集中的。大多数学生会出现相同或是类似的错误，教师们便可以从中总结出学生们在当前知识学习中普遍存在的薄弱环节。以此为据进行重点强化，效果自然理想得多，也为发现问题的过程节省了时间与精力。

三、注重习题变化，有效拓展思维

很多学生认为课本习题没有难度，所以对其重视程度不够。这种看法是有偏颇的。虽然从表面呈现出的效果来看，这些习题比较基础，但是，如果仔细分析便会发现，其中是具有很多可深入、可变化的机会的。如果能够将这些契机利用好，将会大大拓展课本习题的适用范围及效果。

例如，在带领学生们学习过四边形的知识后，课后习题中出现了这样一个问题：求证：顺次连接平行四边形各边中点所得到的四边形是平行四边形。学生们运用所学知识顺利将之解答。然而，我却并没有让这个问题止步于此，而是将其继续变化，请大家试着证明：顺次连接矩形各边中点所得的四边形是菱形；顺次连接菱形各边中点所得的四边形是矩形；顺次连接正方形各边中点所得的四边形是正方形。学生们意外地发现，看似简单的一道课后习题却能够发生如此灵活的变化，并将四边形的各类知识都成功运用起来了。

加入了上述变化，学生们甚至很难相信，这就是原本基础程式的课本习题了。这种习题的变化，离不开教师的敏锐发现与巧妙处理。试想，若是教师们能够将每一个具有典型性的数学问题都进行如此灵活的改变，将它们的潜在功能彻底挖掘出来，以课本内容完成优质教学足矣。

在开展初中数学教学时，教师们总是希望能够在有效的教学时间之内为学生们提供最大的知识信息量，于是便会在基本知识教学完成之后，从课外搜集很多习题来让学生们完成。这种方式未尝不可，但是，很容易由于学习视野从课内向课外的转移，造成学生精力的分散，课外习题也并不一定是完全契合教材内容本身的。因此，如果能从课本习题当中就地取材，挖掘出其中的内涵与精髓，将会让数学教学的效率得到显著提升。潜在功能的发挥，会为教学时效的强化注入强劲动力。