大型繁忙机场场面离场交通流拥堵特征分析

杨磊， 胡明华， 尹苏皖， 张洪海

南京航空航天大学 民航学院， 南京　211106



大型繁忙机场场面离场交通流拥堵特征分析

杨磊， 胡明华*， 尹苏皖， 张洪海

南京航空航天大学 民航学院， 南京211106

阐明机场场面交通流时空演变规律，揭示离场交通流拥堵机理是科学制定场面交通流管控策略的重要基础。采用元胞传输机理论，建立线性滑行道元胞、机坪发散/交叉元胞、汇聚元胞的交通流传输模型，并基于NetLogo系统动力学仿真平台，以广州白云国际机场为例验证了模型的有效性，进而推演分析了离场交通流基础相变特征及其影响机理。研究表明，场面离场交通流存在自由态、亚稳态、拥堵累积态和拥堵死锁态4种基础相态，指出调节与进场率相协调的推出率是有效控制离场交通流密度，缓解场面拥堵的重要手段。研究结果可为大型繁忙机场场面交通智能管控提供一定的理论基础和决策参考。

机场； 交通流； 元胞传输机； NetLogo； 相变； 空中交通管理

空中交通需求与国家空域系统容量、空中交通管理能力之间的矛盾导致空中交通系统抗干扰能力下降，空中交通延误频发，旅客满意度持续下跌[1]。空中交通流量管理是空中交通管理的重要内容，旨在平衡空中交通需求与供给，提高空中交通运行效率，减少航班延误。地面延误程序(Ground Delay Program,GDP)[2]是空中交通流量管理的重要手段之一，旨在控制航班起飞时间以满足到达机场和航路容量的限制。然而，随着地面延误程序的实施，空中交通延误从空中向机场地面转移。大型繁忙机场作为航空运输网络的核心起讫节点，通常呈现物理规模庞大、场面网络复杂、飞行活动高密、交通冲突频发、容需关系失衡以及运行调配困难等特点，其场面交通拥堵矛盾尤为突出，主要表现为离场航空器“时走时停”、离场航班长时间跑道头等待，甚至出现滑行网络死锁导致交通瘫痪等[3]。因此，大型繁忙机场离场交通拥堵疏导已经成为空中交通管理面临的重要挑战[4]，亟需开展离场交通流拥堵特征研究，以期科学指导拥堵疏导实践。

目前，系统性探讨离场交通流拥堵演变特征的研究尚不多见，主要集中在对交通排队和延误等拥堵直观现象的分析。由于机场场面监视雷达数据的封闭性，探索多样的场面运行建模方式成为主要研究手段。机场场面运行建模主要分为3个派别。

1) 动态和随机条件下跑道延误分析[5-7]。以跑道为中心的方法认为跑道是机场容量的主要瓶颈[8]。该类研究通过建立泊松分布下的跑道队列模型预测机场系统期望行为(如新建跑道后延误下降预测等)，对于战略规划等长期计划或者局部扰动下的网络延误研究具有重要意义。然而，该模型在研究航班滑出时间预测方面过于抽象，主要适用于预测整个国家空域系统的宏观运行费用研究，通过建立费用基线对比预测分析网络调整、系统扰动、交通需求场景改变、未来科技或下一代航空运输系统对于空域系统的影响。

2) 离场滑行时间预测建模。Shumsky采用各类解释变量预测航空器滑出时间，如航空公司、离场跑道和离场交通流密度等，同时还建立了跑道服务队列模型[9]；Idris等[10]分析了影响滑行时间的主要因素，并据此建立了滑行时间回归预测模型，但没有明确表述跑道服务过程，因此并未将滑行延误与跑道容量进行联系，无法用于场面交通流管理。基于上述研究成果，美国国家空域系统队列模型试图将场面运行纳入其中，而不是仅将跑道作为服务台。特别地，详细政策评估工具(DPAT)融入随机组件对滑行道相关延误进行分析[11]。然而，该工具滑行延误数值是用户输入的，无法真实推演分析滑行延误演变特征。LMINET工具采用M/M/1队列模型分析滑行延误，其滑行道系统为具有指数服务率的单服务台假设被广泛质疑，仿真数据并未得到验证[12]。因此，DPAT和LMINET均将跑道-滑行道延误预测模型过分简化，对于滑行时间预测结果的准确性不高。

3) 机场微观建模，如SIMMOD、TAAM等仿真工具[13]。通过建立机场详细布局图和运行规则，进行停机位、滑行道和跑道的高保真仿真，但需花费大量的人力和时间成本，且受限于系统的“黑盒”特性，难以扩展验证对比不同运行场景和管控策略下场面交通拥堵特征的差异性。

综上，目前机场场面运行分析领域缺乏权衡精度与成本的交通流建模方法，研究成果并未阐明场面离场交通拥堵机理及其支撑的管控策略。因此，本文面向大型繁忙机场场面拥堵现实问题，将航空器运行视为均质流体，以Lighthill、Whitham和Richards提出的经典LWR交通流模型为基础，借鉴Daganzo元胞传输模型(Cell Transmission Model， CTM)基本建模思想[14-16]，建立机场场面离散差分Eulerian-Lagrangian宏观交通流模型，采用NetLogo系统动力学平台仿真推演离场交通流相变过程，揭示场面离场交通流拥堵成因，提出优化与进场率相协调的推出率是缓解离场交通流拥堵的有效方法。

1　基于可变元胞传输模型(V-CTM)的场面交通流建模

1.1场面可变元胞传输网络

(1)

式中：当节点元胞i与j之间不存在直接链路元胞时，eij=0；反之，若i与j之间存在直接链路时，慢速元胞eij=1/4，中速元胞eij=1/2，快速元胞eij=1。

图1　典型元胞传输模型的点链网络Fig.1　Typical node-link network of cell transmission model (CTM)

可变元胞长度模型可根据平均滑行速度构建并划分差异的元胞长度，原则是尽可能保证单位仿真步长内航空器不能跨元胞滑行，如式(2)所示:

(2)

1.2场面交通流运行建模

1.2.1模型假设

考虑宏观建模要求和机场场面离场运行实际并适当简化，提出如下假设：①确定跑道与机位分配情况下，航空器滑行路径固定；②将场面交通流视为连续均质流体；③航空器在划定的元胞内均匀分布；④不同类型的元胞内交通流平均速度存在差异；⑤场面运行过程中进离场航空器具有相同的优先级。

1.2.2线性滑行道元胞传输模型

考察线性滑行道元胞，航空器流在元胞内均匀单向流动，如图2所示。

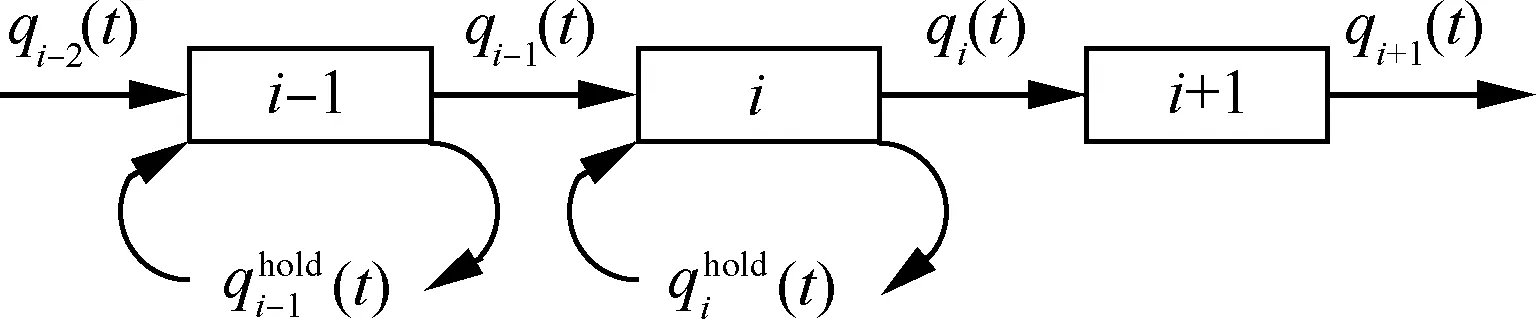
图2　线性滑行道元胞传输模型Fig.2　CTM of linear taxiway

在第t时间片内，元胞i的流入和流出流率qi-1(t)、qi(t)以及存量Ni(t)满足流入、流出流量与存量变化量的守恒关系，即

(3)

通常，上游元胞流出的量受到自身流量和下游元胞可接受流量的约束。由于将场面交通流视为均质流体，因此满足一般流量q、速度v和密度k的基本关系式，即q=kv。因此，qi-1(t)应满足式(4)取值，同理可计算qi(t)dT。

(4)

式中：Ci为元胞i所能同时容纳的最大航空器数量，与元胞长度、机身长度及最小安全间隔有关。不同机型的航空器在场面滑行过程中应保持的最小安全间隔规定如表1所示。

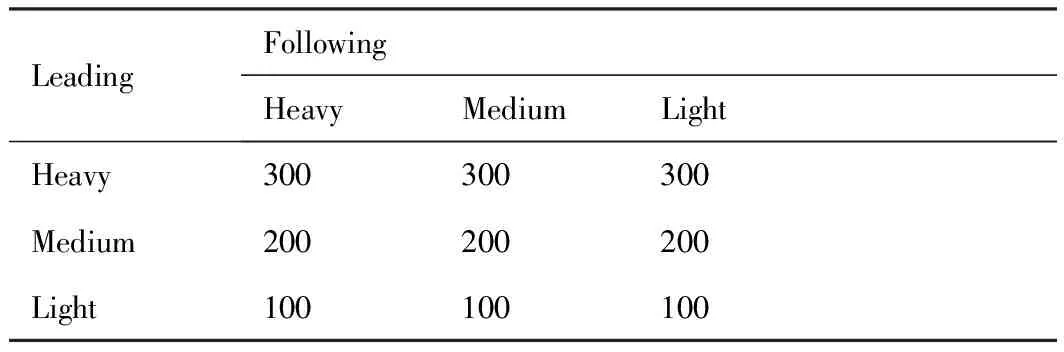
表1　场面滑行间隔规定

(5)

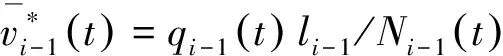
(6)

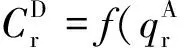
(7)

1.2.3发散/交叉混合滑行道元胞传输模型

机坪区域呈现交通密集运行、进离场交织显著，交通流发散与交叉混合等显著特征，是场面交通流运行最为复杂的区域之一，如图3所示。

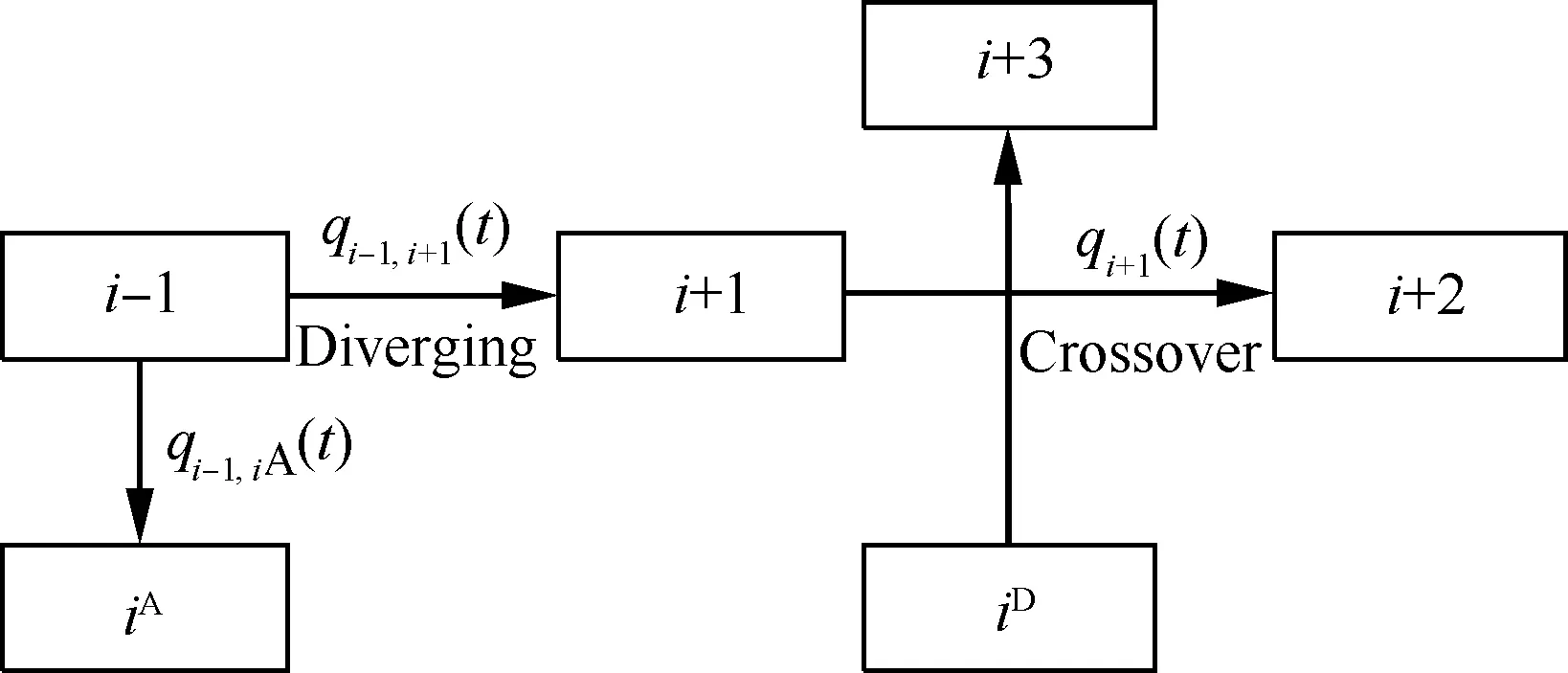
图3　局部机坪滑行道元胞传输模型Fig. 3　CTM of local apron taxiway

(8)

1) 机坪进场发散元胞传输模型

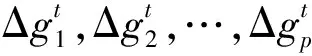
βi-1,iA=

(9)

因此，对于机坪进场元胞iA，其元胞传输模型为

(10)

(11)

qi-1,iA(t)dT=

(12)

(13)

2) 机坪离场交叉元胞传输模型

离场元胞与进场线性滑行道元胞存在交叉，机坪运行冲突加剧，复杂程度较高，如图3所示。因此，机坪离场元胞中交通流的流出率除受离场航班时刻限制外，还受机坪滑行道容量和交叉点容量限制。本文假设交叉点m单位时间内所能通过的最大流量为Qm，时间片内机坪离场元胞最大流出量为

qiD(t)dT=

(14)

元胞i+1的最大流出量为

qi+1(t)dT=

(15)

若QmdT≥qiD(t)dT+qi+1(t)dT，则元胞iD与i+1的流出量不受交叉点容量限制；否则，假定交通流在交叉点通过概率均等，元胞iD与i+1的流出量分别为

qiD(t)dT=

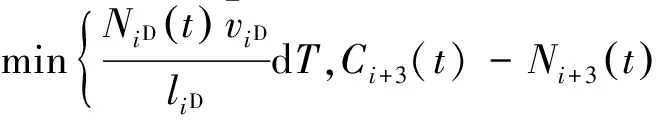
(16)

qi+1(t)dT=

(17)

因此，机坪离场元胞iD的传输模型如式(16)、式(18)与式(19)所示。

(18)

(19)

3) 汇聚滑行道元胞传输模型

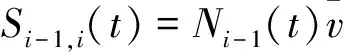
图4　汇聚滑行道元胞传输模型Fig. 4　CTM of convergent taxiway

(20)

(21)

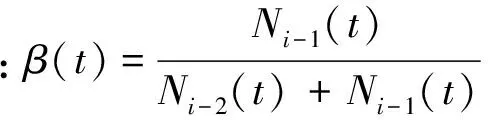
2　实例分析

2.1基线调校

基线调校是指不断调整仿真参数实现仿真结果与实际数据的最佳逼近。本文基于NetLogo系统动力模拟平台[17]，构建广州白云机场场面元胞传输网络与传输规则，选择2014年07月22日13时—17时运行数据进行基线调校。调校时段跑道运行模式为R02R|L相关进近独立离场运行，部分数据如表2所示，场面构型及其元胞传输网络如图5和图6所示。

仿真系统基线参量设定如下：机坪元胞17个，滑行道元胞42个；设置在自由流下主滑行道滑行速度为40 km/h，普通滑行道滑行速度为25 km/h，机坪滑行道滑行速度为10 km/h，仿真步长为30 s；不同进离场比例下的机场运行容量采用文献[18]中分位数回归方法进行计算，结果如图7所示。基线调校后离场率仿真值与真实值之间误差基本在1架次/15 min左右，如图8所示。

2.2离场交通流拥堵特征分析

交通拥堵是某一时空交通供给难以满足交通需求所产生的交通滞留现象[19]。将此概念拓延至机场场面交通，则定义机场场面交通拥堵是机坪、滑行道和跑道系统耦合交通供给难以满足持续交通服务请求所产生的航空器在滑行道缓慢流动、时走时停甚至滞留机位的现象。道路交通流理论中已成熟地通过刻画车流平均速度、密度和流量三类交通流特征参数关联关系阐释道路交通拥堵机理[20]。机场场面交通流与地面交通流具有一定的相似性，如流动方向较为固定；航空器间隔一般由操纵者自行掌握；流动过程中存在汇聚、发散和交叉等复杂现象。然而，场面交通流具有其特殊性，如场面交通流可简单分为进场交通流和离场交通流两类，受场面物理结构和运行规则的限制，两者存在严重的相互制约；离场交通流最终形成跑道离场交通流，离场交通流最大流量受跑道容量限制。因此，本文根据机场场面运行特征，构建场面离场交通流特征指标以刻画离场交通流拥堵现象，解释拥堵成因和演变机理。

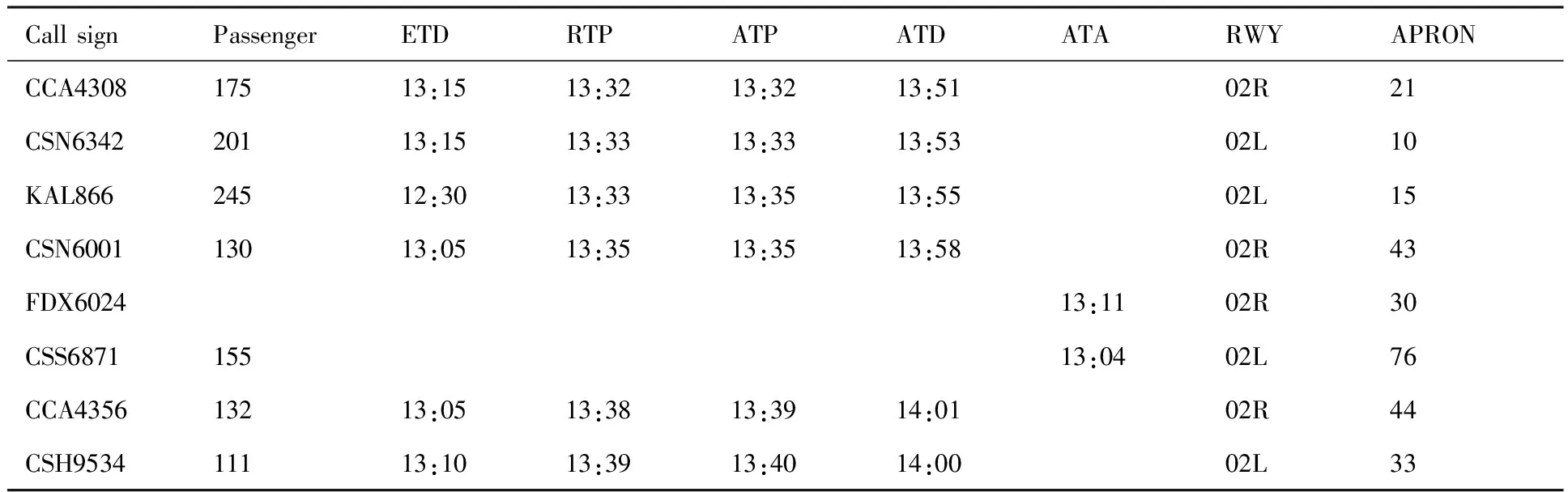
表2　广州白云机场仿真时段部分数据

图5　广州白云机场场面网络Fig. 5　Surface network of Guangzhou Baiyun International Airport　

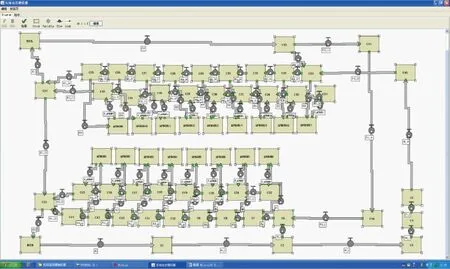
图6　广州白云机场场面元胞传输网络Fig. 6　CTM network of Guangzhou Baiyun International Airport　

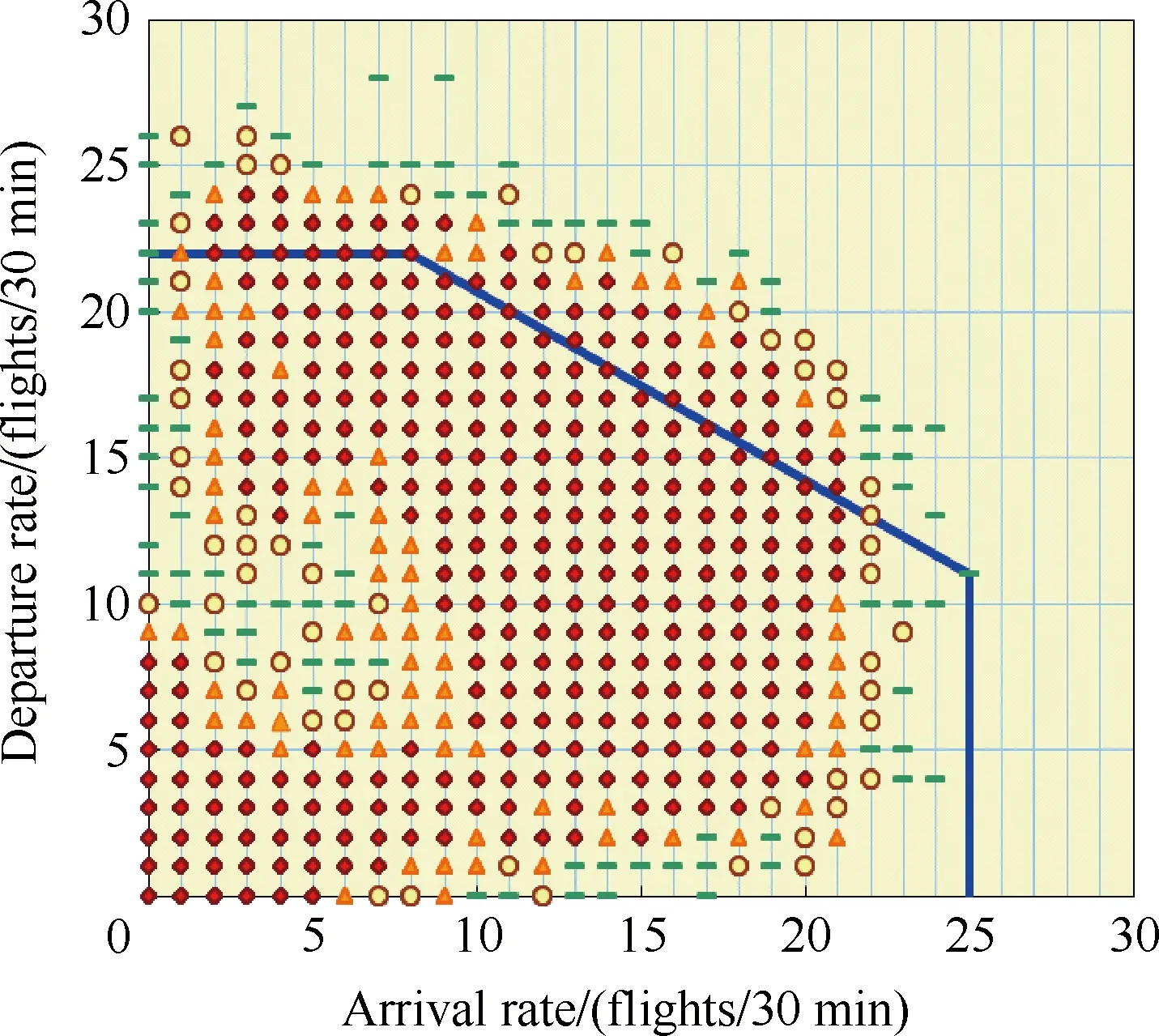
图7　广州白云机场运行容量曲线Fig. 7　Capacity envelop of Guangzhou Baiyun International Airport　

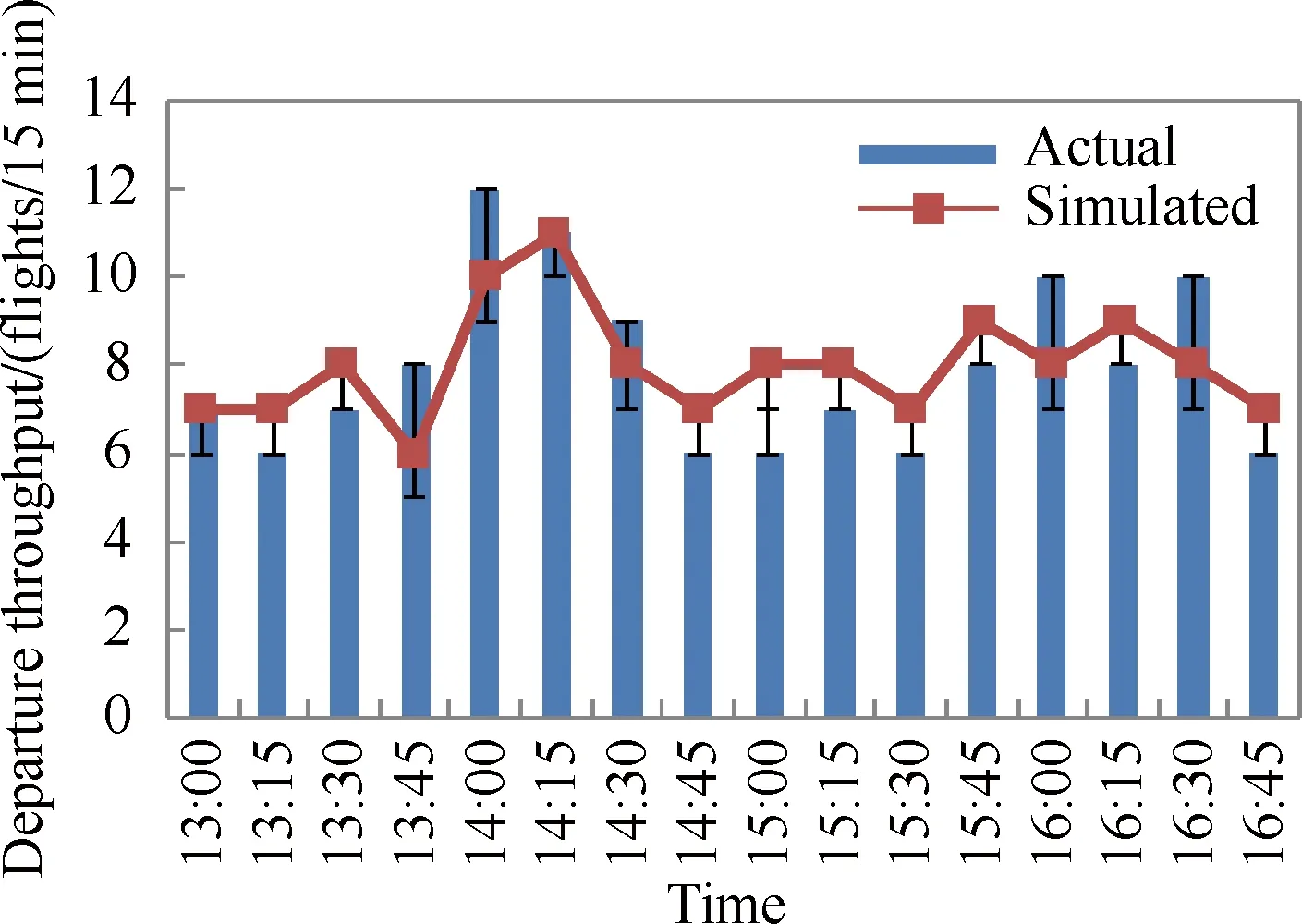
图8　基于元胞传输模型的广州白云机场场面仿真系统基线图Fig. 8　Baseline of Guangzhou Baiyun International Airport surface simulator based on CTM

1) 离场交通流特征参量定义

(1) 离场交通流量： 指统计时段内，跑道起飞的航空器总量。

(2) 离场交通流密度： 指统计时段内，处于滑行状态的场面离场航空器总量。实际运行过程中，离场交通流密度一方面由飞行计划决定，一方面管制员根据当前场面运行状况和跑道放行条件，通过控制离场航班的推出时刻适度调节需求，防止跑道头等待航空器超过阈值。

(3) 离场航班平均滑行速度： 指统计时段内，机场场面处于滑行过程中所有离场航空器的平均滑行速度，可视为整个离场交通流的平均流速。

2) 离场交通流基础相态分析

结果表明，离场交通流存在自由态、亚稳态、拥堵累积态和拥堵死锁态，如图9所示。自由态阶段，离场交通流量随离场交通流密度线性增加，场面滑行几乎没有冲突，平均滑行速度处于高位。随着离场交通流密度的不断增加，由于跑道容量受限，离场流量增加率逐步放缓并在临界离场交通密度点达到饱和，即亚稳态点。亚稳态下，虽然交通流运行效率最高，但交通流并不稳定，对于离场密度增量十分敏感，并快速进入拥堵累积阶段。拥堵累积阶段整体交通流速急剧下降，离场航班的滑行时间急剧升高。随着拥堵不断累积，机场场面离场滑行航空器数量逐步增加直至饱和，此时场面上无法容纳更多的离场航空器，达到场面离场交通流密度峰值，进入交通流拥堵“死锁”状态。此时，进场交通流由于无法落地也将产生大面积空中等待，机场场面交通拥堵向空中蔓延。

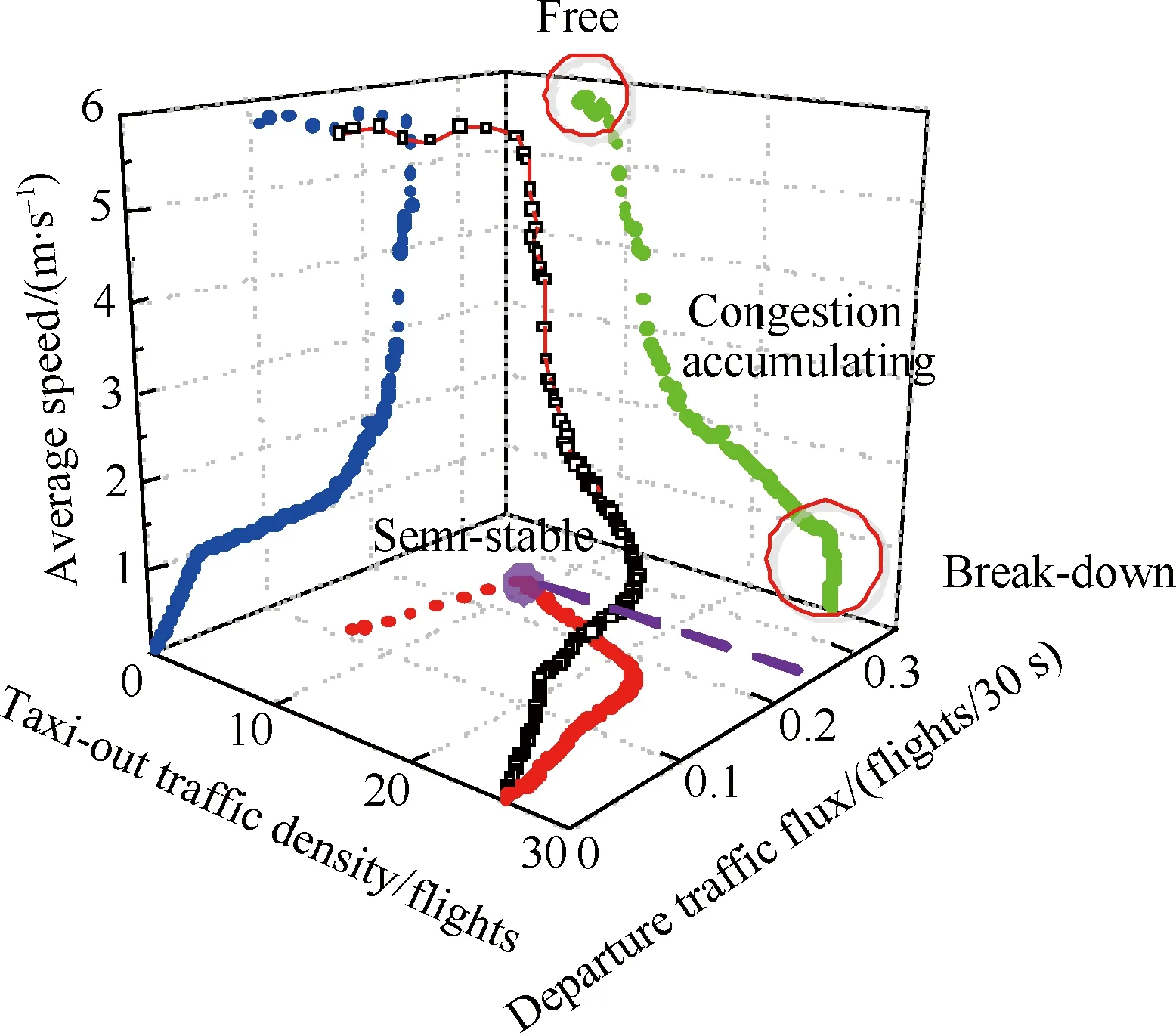
图9　离场交通密度、离场交通流量和平均离场滑行速度两两投影关系图Fig. 9　Pairwise relations of taxi-out traffic density, departure traffic flux and average speed

3) 临界离场交通流密度影响分析

离场交通流存在4类基础相态是最大推出需求下的理论理想结果。然而，由于空中交通具有极强的计划性，因此实际运行中拥堵死锁状态往往不可能发生。亚稳态点是交通流从自由走向拥堵的转折点，也是离场交通流量达到峰值的临界点，是离场交通流拥堵最具价值的特征点，也是制定拥堵疏导策略的关键决策点。因此，本节针对亚稳态特征，定义离场交通流亚稳态点为临界离场交通流密度点，并研究不同交通场景下临界离场交通流密度点的变化规律。

本文以广州白云机场一周航班计划为基础进行场面交通流仿真。仿真结果表明，广州白云机场平均滑行时间为18 min，滑行时间符合高斯分布，拟合方程和相关参数如图10所示。

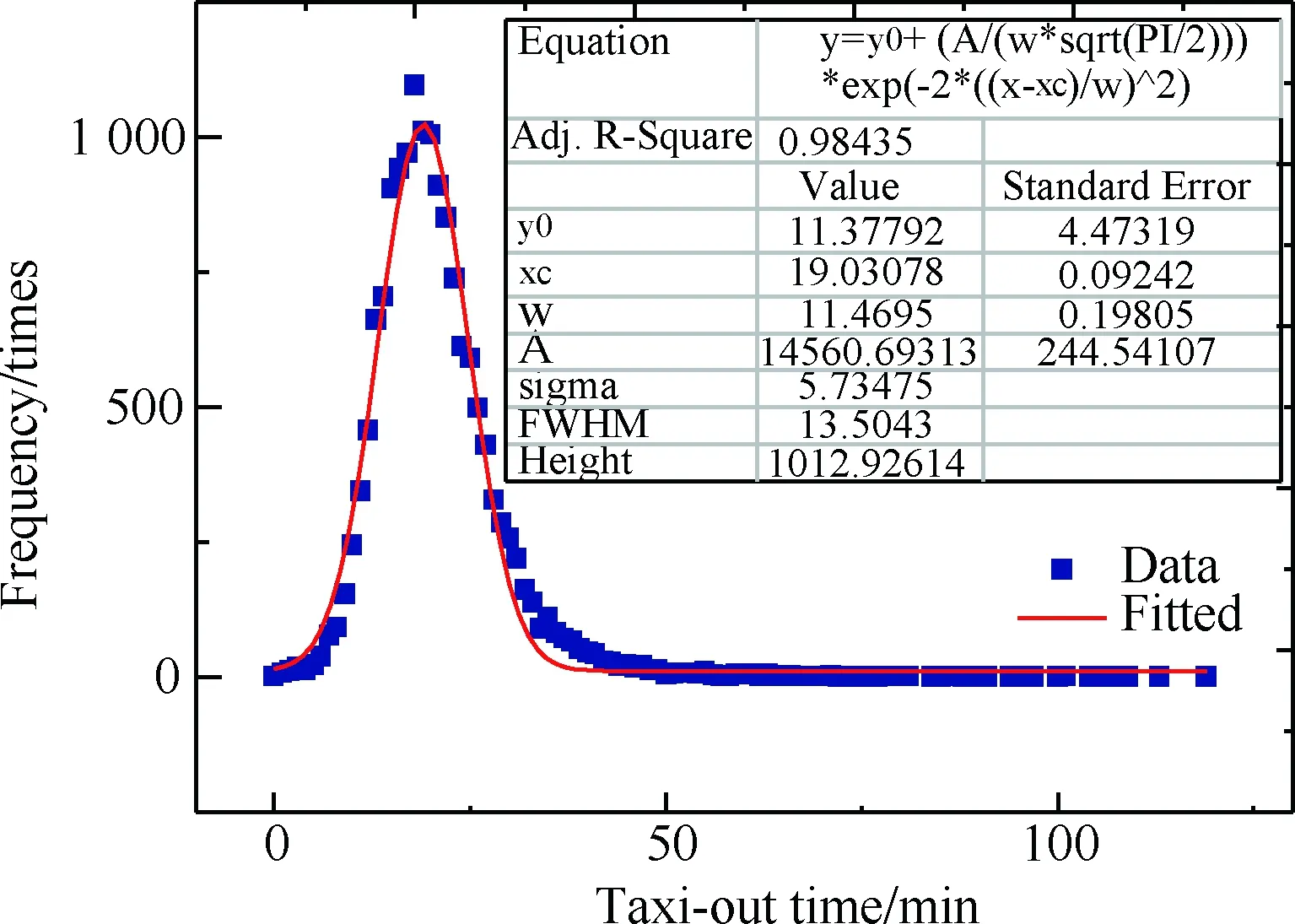
图10　广州白云机场离场航班滑行时间分布Fig. 10　Taxi-out time distribution of Guangzhou Baiyun International Airport

仿真时段中离场交通流密度最大值为18架次，交通流在自由态和拥堵累积态之间切换；同一进场率下离场交通流量与离场交通流密度具备显著的凸函数性质，并且在临界离场交通流密度点处离场交通流量达到最高值；临界离场交通流密度对于进场率具有敏感性，呈现进场率越大临界离场交通流密度越小的趋势，如图11所示。

具体来说，进场率从0架次/15 min增加至14架次/15 min，临界离场交通流密度从14架次阶梯减少至8架次，离场最大吞吐量从10架次/15 min减少至7架次/15 min；由于跑道进离场容量的耦合效应，进场率的增加势必带来离场容量的降低，因此，在同样的离场交通流密度下交通流更易进入亚稳态甚至拥堵累积态，如图12所示。

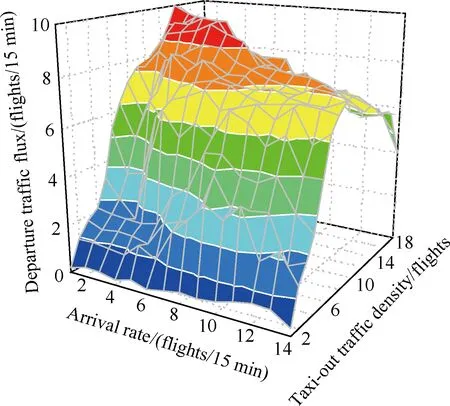
图11　不同进场率下离场交通流量和离场交通流密度关系Fig. 11　Relationship between departure traffic flux and taxi-out traffic density at various arrival rates

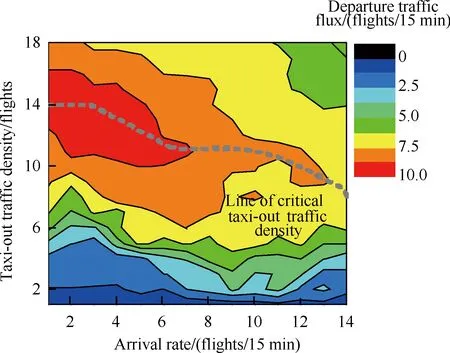
图12　进场率与临界离场交通流密度关系热图Fig. 12　Heat map of relationship between arrival rate and critical taxi-out traffic density

综上，在同一运行场景不同进场率水平下，离场交通流在相同离场交通流密度时可能处于不同的相态；进场率决定了某一时段内临界离场交通流密度点及其对应的离场最大吞吐量。因此，控制与进场率相适应的离场航班推出率是动态调节机场场面离场交通流密度，缓解离场交通拥堵的重要手段。

3　结　论

1) 借鉴元胞传输理论，考虑机场场面网络分合关系和进离场交通流运行实际，建立机场场面离散差分Eulerian-Lagrangian宏观交通流模型，并依托NetLogo系统动力学仿真平台开发兼具精度与效率的机场场面交通流仿真系统，以广州白云机场双跑道混合运行为例，推演了离场交通流密度、离场平均滑行速度和离场交通流量之间的关联关系，阐明离场交通流蕴含的4个基本相态，重点剖析了临界离场交通流密度(亚稳态)影响机理，提出了控制与进场率相适应的离场航班推出率是动态调节机场场面离场交通流密度，缓解离场交通拥堵的重要手段。

2) 本文研究成果可为完善空中交通流理论奠定部分基础，为实施空中交通自动化、智能化管控提供理论依据；对于协同决策环境下广州白云机场离场滑行时间动态预测、机位协同释放策略等空中交通运行管理实践具有一定的理论指导意义。

3) 在本文的研究基础上，可将宏观交通流仿真理念扩展至全国空域系统，系统性推演分析空中交通流基本相变特征以及延误传播规律，逐步建立健全空中交通流理论体系，科学指导一体化、智能化空中交通系统的建设发展。

[1]LORDAN O, SALLAN J M, SIMO P, et al. Robustness of the air tranport network[J]. Transportation Research Part E: Logistics & Transportation Review, 2014, 68(68): 155-163.

[2]TANDALE M D, SENGUPTA P, MENON P K, et al. Queuing network models of the national airspace system[C]//The 26th Congress of International Council of the Aeronautical Sciences. Reston: AIAA, 2008: 1-14.

[3]HANSEN M. Micro-level analysis of airport delay externalities using deterministic queuing models: A case study[J]. Journal of Air Transport Management, 2002, 8(2): 73-87.

[4]BALAKRISHNAN H, JUNG Y. A framework for coordinated surface operation planning at dallas-fort worth international airport[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA,2007: 230-243.

[5]KIVESTU P A. Alternative methods of investigating the time dependent M/G/k queue[D]. Massachusetts: Massachusetts Institute of Technology, 1976.

[6]MALONE K M. Dynamic queueing systems: Behavior and approximations for individual queues and for networks[D]. Massachusetts: Massachusetts Institute of Technology, 1995.

[7]PYRGIOTIS N, MALONE K M, ODONI A. Modelling delay propagation within an airport network[J]. Transportation Research Part C: Emerging Technologies, 2011, 27(2): 60-75.

[8]IDRIS H R, DELCAIRE B, ANAGNOSTAKIS I, et al. Identification of flow constraint and control points in departure operations at airport systems[C]//AIAA Guidance, Navigation and Control Conference. Reston: AIAA,1998: 947-956.

[9]SHUMSKY R A. Dynamic statistical models for the prediction of aircraft take-off times[D]. Massachusetts: Massachusetts Institute of Technology, 1995.

[10]IDRIS H, CLARKE J P, BHUVA R, et al. Queuing model for taxi-out time estimation[J]. Air Traffic Control Quarterly, 2002, 10(1): 1-22.

[11]WIELAND F. The detailed policy assessment tool (DPAT)[C]//Proceedings of Spring INFORMS Conference, 1997: 654-664.

[12]LONG D, LEE D, JOHNSON J, et al. Modeling air traffic management technologies with a queuing network model of the national airspace system: NAS 1.26: 208988[R]. Alexandria: NASA Center for AeroSpace Information, 1999.

[13]ODONI A R, BOWMAN J, DELAHAYE D. Existing and required modeling capabilities for evaluating ATM systems and concepts: NAS 1.26: 204978[R]. Alexandria: ATM Systems Strategic Traffic Management Plan and control Air Transportation, 1997.

[14]DAGANZO C F. The cell transmission model, Part II: Network traffic[J]. Transportation Research Part B, 1995, 29(2): 79-93.

[15]ZHANG H H, XU Y, YANG L, et al. Macroscopic model and simulation analysis of air traffic flow in airport terminal area[J]. Discrete Dynamics in Nature and Society, 2014(6): 1-15.

[16]张洪海, 杨磊, 别翌荟, 等. 终端区进场交通流广义跟驰行为与复杂相变分析[J]. 航空学报, 2015, 36(3): 949-961.

ZHANG H H, YANG L, BIE Y H, et al. Research on generalized following behavior and complex phase-transition law of approaching traffic flow in terminal airspace[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 949-961 (in Chinese).

[17]戴文雯, 别翌荟, 张洪海, 等. 基于 NetLogo 的终端区交通流仿真[J]. 航空计算技术, 2014, 44(1): 30-33.

DAI W W, BIE Y H, ZHANG H H, et al. Simulation of air traffic flow based on NetLogo[J]. Aeronautical Computing Technique, 2014, 44(1): 30-33 (in Chinese).

[18]RAMANUJAM V, BALAKRISHNAN H. Estimation of arrival-departure capacity tradeoffs in multi-airport system[C]//The 48th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2009: 2534-2540.

[19]LIGHTHILL M J, WHITHAM G B. On kinematic waves. II. A theory of traffic flow on long crowded roads[J]. Highway Research Board Special Report, 1964, 299(1178): 281-345.

[20]BELLOMO N, COSCIA V, DELITALA M. On the mathematical theory of vehicular traffic flow: Fluid dynamic and kinetic modelling[J]. Mathematical Models and Methods in Applied Science, 2002, 12(12): 1801-1843.

杨磊男， 博士研究生。主要研究方向： 飞行流理论与智能管控技术。

Tel: 025-52112669

E-mail: laneyoung49@hotmail.com

胡明华男， 硕士， 教授， 博士生导师。主要研究方向： 国家空域系统规划、管理与评估， 飞行流量管理， 空中交通管理系统信息化与智能化。

Tel: 025-52112669

E-mail: minghuahu@263.net

尹苏皖女， 硕士研究生。主要研究方向： 机场终端区容量评估。

Tel: 025-52112669

E-mail: 739688191@qq.com

张洪海男， 博士， 副教授， 硕士生导师。主要研究方向： 飞行流理论与调控技术、空管协同化与智能化以及复杂空中交通系统。

Tel: 025-52112669

E-mail: zhh0913@163.com

Characteristics analysis of departure traffic flow congestion inmega-airport surface

YANG Lei, HU Minghua*, YIN Suwan, ZHANG Honghai

College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing211106, China

Expounding traffic flow spatial-temporal evolution laws on mega-airport surface and revealing departure traffic flow congestion mechanism are the significant basis of airport surface traffic flow management and control. By adopting cell transmission model, normal taxiway cells, apron cells and convergent cells operation model were established. Based on the NetLogo’s system dynamics simulation platform, Guangzhou Baiyun International Airport surface operation was macroscopically simulated. By comparing the actual and simulation data, the proposed model was validated to be accurate and efficient. Simulation results show that departure traffic flow contains four basic phases: free, semi-stable, congestion accumulating and break-down, and adjusting pushback rate according to the arrival rate will be a critical method in controlling departure demand and alleviate traffic congestion. This research achievement may provide a theoretical basis and decision reference for intelligent traffic control in mega-airport.

airport; traffic flow; cell transmission model; NetLogo; phase-transition; air traffic management

2015-06-19; Revised: 2015-09-21; Accepted: 2015-10-18; Published online: 2015-10-2117:09

s： National Natural Science Foundation of China (61104159); Natural Science Foundation of Jiangsu Province (BK20131366)

. Tel.: 025-52112669E-mail: minghuahu@263.net

2015-06-19; 退修日期: 2015-09-21; 录用日期: 2015-10-18;

时间: 2015-10-2117:09

www.cnki.net/kcms/detail/11.1929.V.20151021.1709.004.html

国家自然科学基金 (61104159)； 江苏省自然科学基金 (BK20131366)

.Tel.: 025-52112669E-mail: minghuahu@263.net

10.7527/S1000-6893.2015.0280

V355; U8

A

1000-6893(2016)06-1921-10

引用格式： 杨磊， 胡明华， 尹苏皖， 等． 大型繁忙机场场面离场交通流拥堵特征分析[J]． 航空学报, 2016, 37(6): 1921-1930. YANG L, HU M H, YIN S W, et al. Characteristics analysis of departure traffic flow congestion in mega-airport surface[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1921-1930.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20151021.1709.004.html