基于混合体制雷达网的弹道目标微特征及外形参数提取
李靖卿, 冯存前, 孙宏伟, 贺思三
1.空军工程大学 防空反导学院, 西安 710051 2.中国人民解放军 93764部队, 包头 075000
基于混合体制雷达网的弹道目标微特征及外形参数提取
李靖卿1,2, 冯存前1,*, 孙宏伟2, 贺思三1
1.空军工程大学 防空反导学院, 西安710051 2.中国人民解放军 93764部队, 包头075000
针对弹道中段目标微特征难以识别与分辨的问题,提出了一种基于低分辨雷达和高分辨雷达相结合的混合体制雷达网的有翼弹道目标微特征及外形参数提取方法。依据非线性信号参量可分离模型,利用非线性最小二乘估计方法解算出有翼弹道目标群各散射中心的幅相参数,结合不同雷达提取的微特征的关联性,利用散射中心关联处理实现了各类散射中心的分离。在此基础上,利用弹道目标的微特征,结合弹道目标各散射中心的相对位置关系,重构出各目标的三维微特征及各散射中心的三维位置矢量,进而估计出目标的进动特征和结构参数。仿真结果表明:当信噪比(SNR)为5 dB时,该方法的重构精度保持在92%左右。
微特征; 混合体制雷达网; 匹配; 特征提取; 弹道目标
弹道目标识别是战略预警能力和反导作战能力的集中体现,组网雷达作为弹道目标识别的倍增器,是解决弹道群目标突防、有源无源干扰以及单基地雷达搜索区域限制的有效途径[1-3]。自Chen[3]首次将微动概念引入到雷达目标识别以来,利用目标微特征进行目标识别的方法就成为雷达目标识别领域的一个研究热点。
随着战场环境的日趋复杂和目标特征控制技术的应用,仅依靠单基地雷达来实现目标的探测及分类识别显然是不够的,组网雷达技术为弹道目标微特征的研究和应用提供了一个新的突破口。Chen指出:目标的微多普勒特征并不受限于距离分辨,而且多基地雷达可以获得比单基地雷达更为完整的微多普勒特征或频移[3]。Smith等[4]讨论了利用多站雷达网获取的微多普勒信息进行目标分类的可行性。Vespe等[5]指出利用多基地雷达的多视角特性可以有效弥补单部雷达获得的高分辨距离像(HRRP)信息的缺失和不足,有利于进行空间目标识别。韩勋等[6]根据频谱熵将低分辨雷达网获取的多视角微多普勒信息进行匹配处理,从而实现了空间目标的微特征提取,但抗噪性不强。向道朴[7]利用独立成分分析(Independent Component Analysis, ICA)算法和时频分析相结合的方法从低分辨雷达网获取的微多普勒信息中分辨出群目标,但分辨效果有限。张栋等[8]解算出进动目标HRRP对应的线性和信号,利用高分辨雷达网提取出目标的微动参数。Luo等[9]利用分布式组网雷达的多视角特性,实现了有翼弹道目标的三维重构,并指出有翼弹道目标相比无翼弹道目标而言,其尾翼自旋引起的回波调制不能忽略,与锥旋共同作用产生的合成调制将更为复杂。Ai等[10]利用T/R-R(Transmitter/Receiver-Receiver)双基地逆合成孔径雷达(ISAR),结合扩展Hough变换和快速傅里叶变换(FFT)算法,实现了二维高分辨ISAR成像。在实际应用中,高性能低分辨雷达已大量应用于反导预警雷达,其实时性较好,但分辨率略有不足,探测能力有限;而宽带高分辨雷达主要用于舰船、空天目标的精细监视与成像识别,其价格昂贵,短时间内难以大量装备,且占用信息处理资源较大,实时性不强[11-12]。因此,有效发挥现有低分辨雷达的优势,可以更好地解决当前弹道目标的识别问题。美国林肯实验室就利用Millstone雷达获取的窄带雷达散射截面积(Radar Cross Section, RCS)特征去评估宽带高分辨干草堆雷达Haystack及其辅助雷达HAX得到的ISAR像(包括有效负载、旋转频率等参数),实现了高/低分辨雷达的融合识别[12]。需要指出的是,文中的低分辨雷达并非常规远程预警雷达,而是经过升级改造后的高性能反导预警雷达。
本文首先分别分析了高/低分辨雷达获取的微特征,构建了信号参量可分离模型;然后利用散射中心关联处理方法,实现了混合体制雷达网中各类散射中心的分类;最后利用分布式处理和加权平均相结合的方法,实现了弹道目标的微特征及外形参数提取。
1 弹道目标微特征分析
对于弹道目标而言,其强散射中心数量有限,本文主要对有翼锥形弹头进行分析。在光学区,有翼锥形弹头的多散射中心一般由锥顶散射中心和底面边缘尾翼散射中心构成[9],此处暂不考虑底面边缘结构产生滑动的影响。针对多散射中心目标模型,本文构建了混合体制雷达网系统,如图1 所示。
雷达网共包含Inarrow部低分辨雷达和Iwide部高分辨雷达。为了方便表述,这里假设各部子雷达均为单基地雷达。O′-XYZ为雷达网坐标系,O-xyz为弹体坐标系,z轴为目标自旋轴的指向,O-x′y′z′ 为相对坐标系,且平行于O′-XYZ,O为目标质心。目标的自旋频率和锥旋频率分别为ωs和ωc,其矢量形式为ωs和ωc。
假设目标共包含M个散射中心,在t时刻,雷达网中任一部雷达I与目标上第m个散射中心的位置矢量为
RIt=RI+ΔRm tI=1,2,…,Inarrow+Iwide
(1)
式中:RI为平动分量;ΔRm t为微动分量。则第m个散射中心的径向距离为[3]
(2)
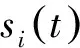
i=1,2,…,Inarrow
(3)
对式(3)进行采样处理,得到第k个脉冲采样后的信号为
(4)
(5)
(6)式中:ω=[ωcωsωc+ωsωc-ωs]为频率信息;fi m为第m个散射中心对应的微多普勒信息;ai m和Hnarrow分别为第i部低分辨雷达获取的第m个散射中心对应的幅度和相位信息,且满足:
(7)
式中:N为雷达采样次数;Δt为采样时间间隔;E4×1为4×1维的单位矩阵。为方便表述,ai m可简写为
(8)
式中:Λ为ai m的参量空间;ai m的具体表达式见文献[13]。不难看出,弹头的微多普勒fdi可以等效为几个正弦分量的叠加,ai m与弹头进动参数、结构参数及雷达视角有关。
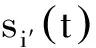
i′=1,2,…,Iwide
(9)
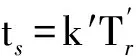
(10)
式中:r为距离像峰;ΔR为目标与参考点间的距离。不难看出,弹道目标HRRP的峰值点位于[13]:
(11)
其矩阵形式可以表示为
(12)
式中:EN×1为N×1维的单位矩阵;ri′m为第i′部高分辨雷达获得的微动信息;bi′m和Hwide分别为第i′部高分辨雷达获得的第m个散射中心的幅度和相位信息;Λ′为bi′m的参量空间,bi′m的具体表达式见文献[13]。
2 雷达网的散射中心关联处理
由于弹道目标回波对应的微特征通常表征为时变非平稳的多分量信号,其包含的各散射中心对应的微动分量一般会相互叠加在一起。因此,有效从组网雷达中获取同一个目标所包含的不同类型的散射中心信息至关重要。为了有效发挥现有低分辨雷达的优势,解决当前弹道目标的识别问题,本文首先采用一致性聚类分析方法将高、低分辨雷达获取的微动信息进行数据关联处理,以达到不同类型的散射中心分类的目的。
2.1微动信息获取
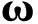
(13)
式中:gm和H分别为第m个散射中心对应的微多普勒分量和相位信息。
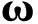
(14)
式中:fm和rm分别为低、高分辨雷达获得的第m个散射中心对应的微动信息。
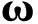
然而,高分辨雷达获取的HRRP姿态敏感性较强,不利于数据的稳健处理。考虑到弹道目标强散射中心较少且分布稀疏,可以忽略同一距离单元内交叉项干扰的影响,直接利用时域抽取法抽取任意快时间tq处的行信号,即对式(9)的快时间tq进行赋值,然后对相位项关于慢时间ts进行求导,经时频变换就可以观测到目标完整的微多普勒分量,这样可以有效地降低HRRP对姿态角的敏感性,得到更稳定的微多普勒信息:
(15)
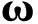
2.2微动信息关联与分类
研究表明[18],对同一散射中心而言,低分辨雷达获取的时频信息(微多普勒曲线)可以等效为高分辨成像雷达获取的距离像曲线的导函数,这就给混合体制雷达网中的数据关联提供了理论依据。由文献[6]可知,当信噪比较高(不小于 5 dB)时,低分辨雷达得到的微特征的提取精度可以达到94%以上;而对于高分辨雷达而言,它可获得98%左右的特征提取精度(信噪比可以达到0 dB)[9]。因此,当信噪比较高时,低分辨雷达的特征提取精度与高分辨雷达的特征提取精度相差不大,可以进行数据关联处理。
考虑到高、低分辨雷达获取的微动信息存在一定的精度误差,若对混合体制雷达网获得的所有幅度和相位信息直接进行聚类分析,就发挥不出混合体制雷达网的整体优势。因此,本文先分别对不同体制雷达获取的幅度和相位信息进行聚类分析,然后对不同体制雷达对应的各个类进行分类处理,具体分类过程如下。

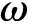

步骤2预测聚类中心。对同一时间段内同一体制雷达获得的各条微多普勒曲线进行δ -ρ一致性聚类分析[19],且满足:
(16)
(17)
式中:du w为O -ωcωs平面内任意两个投影点的距离;u和w为平面内不同的投影点;ρu为局部聚类密度,主要表示间距小于截止间距dc的投影点的个数;δu为该投影点到更高密度聚类区域的最大距离;dc为截止间距,决定着各聚类区域的划设。
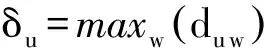

(18)
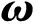
通过以上处理,便可准确区分出不同类型的散射中心,并较好地分离出多部雷达获取的同一类型散射中心对应的微动信息,有效实现目标散射中心的分类。
3 弹道目标的微特征及外形参数提取
由第2节的分析可知,在完成散射中心分类处理后,可以得到多部雷达获取的同一类散射中心的微动信息,但该信息无法有效反映出目标的可视化结构特征和目标微运动的差异性。因此,在完成散射中心分类的基础上,根据弹道目标的几何结构特征和各散射中心的位置参数,本节考虑利用混合体制雷达网观测的数据进行弹道目标的微特征及外形参数提取,为目标识别提供依据。
3.1三维锥旋矢量提取
由于弹头的锥顶散射中心位于自旋轴上,它仅受锥旋频率的影响,满足正弦规律;而其他散射中心还受到自旋频率的影响,呈非正弦规律[13]。根据2.2节步骤1的判别方法,易判断出弹头锥顶散射中心的微多普勒分量。通常认为,自旋轴与锥旋轴的夹角保持相对不变,即进动角具有相对稳定性[13]。
由文献[13]可知,若锥顶用A表示,则锥顶散射中心的幅度信息满足:
(19)
考虑到低分辨雷达应用广泛,而高分辨雷达应用相对较少的现状,这里以多部低分辨雷达获取的微动信息建立方程组:
(20)
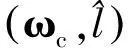
(21)
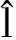
3.2强散射中心初始位矢解算
根据3.1节的分析,结合进动角的相对不变性,不难联立方程组为
(22)
(23)
由于式(23)仅包含3个未知参量(rAx′,rAy′,rAz′),因此,只需要1部高分辨雷达获取的幅度和相位信息求解即可。一般而言,弹道目标属于刚体目标,其形态保持相对不变。当刚体运动时,它的各散射中心之间存在一定的关系,以两翼平底锥形弹头为例来进行说明。
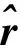
(24)
3.3进动参数及结构参数估计
根据夹角公式,结合式(20)和式(24),可以求出目标的进动角参数为
(25)
(26)
最后根据式(21)的加权求平均方法,分别得到目标长度及半锥角的最终值。如果目标底面边缘包含多个尾翼散射中心,底面半径还需满足:
(27)
3.4基本实现流程
通过以上的分析,可以看出本文的方法比较符合当前雷达的应用现状,充分发挥了低分辨雷达的应用数量及探测范围的优势,同时兼顾了高分辨雷达成像精度高的特点,通过数据关联处理,有效地解决了高/低分辨雷达数据精度差异较大、难以有效融合识别的问题,基本步骤如下。
步骤1针对混合体制雷达网获取的微动信息,根据式(14),利用信号参量可分离模型求得幅度和相位信息。
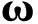
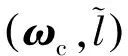
步骤5根据式(20)和式(24),求出目标的进动角参数θ。
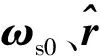
步骤7根据式(27)的判决准则,完成该各弹道目标真实尺寸的微特征及外形参数提取。
4 仿真分析
4.1算法有效性验证
混合体制雷达网中共有3部高性能低分辨雷达和1部高分辨雷达,观测时间均为2 s。其中,低分辨雷达发射单频信号,载频分别为6.5、8.5和11.5 GHz,脉冲重复频率均为600 Hz,编号分别为1、2、3,在O′-XYZ中的坐标分别为(80,40,1)、(40,80,2)和(20,20,0) km,距离分辨率均为15 m。高分辨雷达发射LFM信号,载频为10 GHz,带宽为1 GHz,脉宽为50 μs,脉冲重复频率为500 Hz,编号为4,在O′-XYZ中的坐标为 (0,0,6) km,距离分辨率为15 cm。
假设空间中存在单个目标,且包含3个强散射中心。该目标的锥旋频率为0.4 Hz,它在O-x′y′z′上的指向为(20°, 65°),且绕着x、y和z轴以初始欧拉角 (75°, 30°, 20°)和自旋频率(0,0,1.1) Hz作自旋运动,它的散射中心在O-x′y′z′上的坐标分别为A(0,0,1.6) m、v1(-0.4,-0.3,-0.4) m、v2(0.4,0.3,-0.4) m,质心O在O′-XYZ上的位矢为(200,200,100) km。假设平动分量已完全补偿,散射系数由随机函数randn生成,且信噪比均为5 dB。
由文献[20]可知,现有雷达网多采用GPS卫星链路双向授时,时间同步精度可以达到2 ns左右,远低于文中设置的高分辨雷达发射脉宽50 μs。此时ωct、ωst中包含的时间同步误差的量级仅为10-7~10-9,可以忽略不计。而对于地基雷达网而言,雷达网中各子雷达的位置相对固定,此时暂不考虑空间同步的影响。
图2(a)~图2(d)分别为混合体制雷达网中不同体制雷达获得的微多普勒曲线,对图2(d)的距离像信息进行时域抽取处理,可以得到目标群中不同子目标的时频信息。图2(e)为雷达4在第20个快时间单元获取的目标的时频信息。比较图2(a)和图2(e),目标的微多普勒变化幅度存在明显差异,但微多普勒的周期性变化规律基本一致。
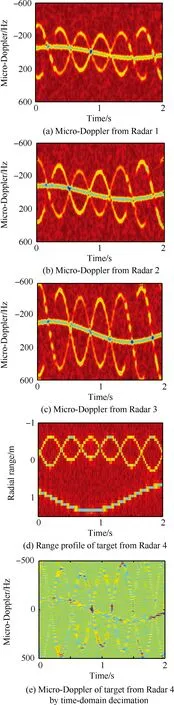
图2 混合体制雷达网中各部雷达对应的微多普勒曲线Fig.2 Micro-Doppler curves by each radar in hybrid-scheme radar network
表1雷达2获取的某一散射中心对应的微动频率
Table 1Micro-motion frequency of some scattering center by Radar 2
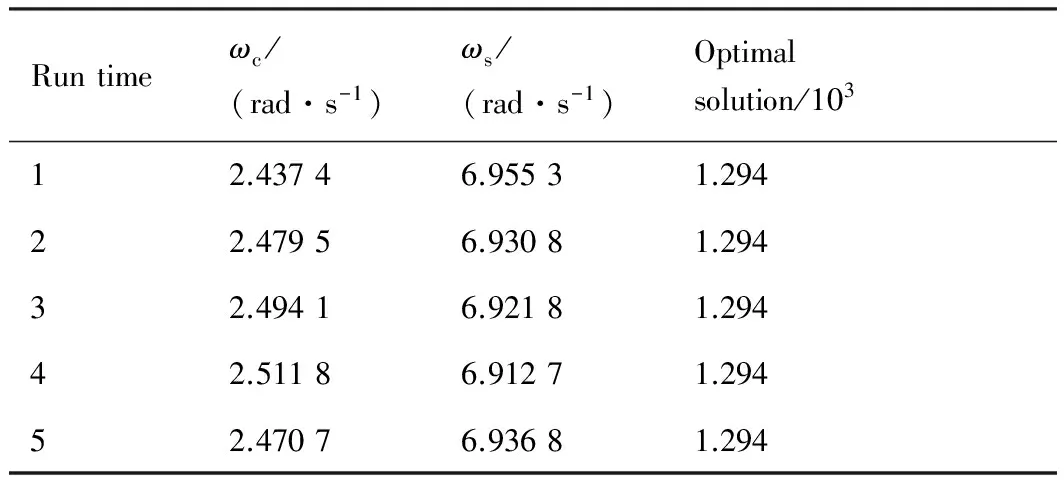
Runtimeωc/(rad·s-1)ωs/(rad·s-1)Optimalsolution/10312.43746.95531.29422.47956.93081.29432.49416.92181.29442.51186.91271.29452.47076.93681.294
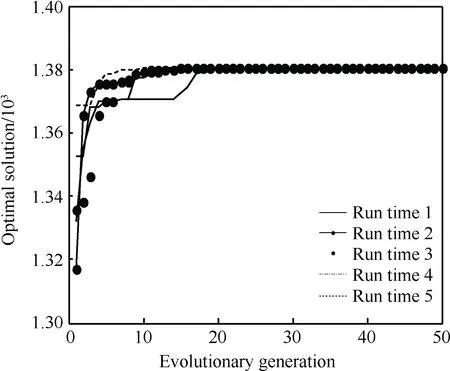
图3 进化过程图Fig.3 Evolutionary process diagram
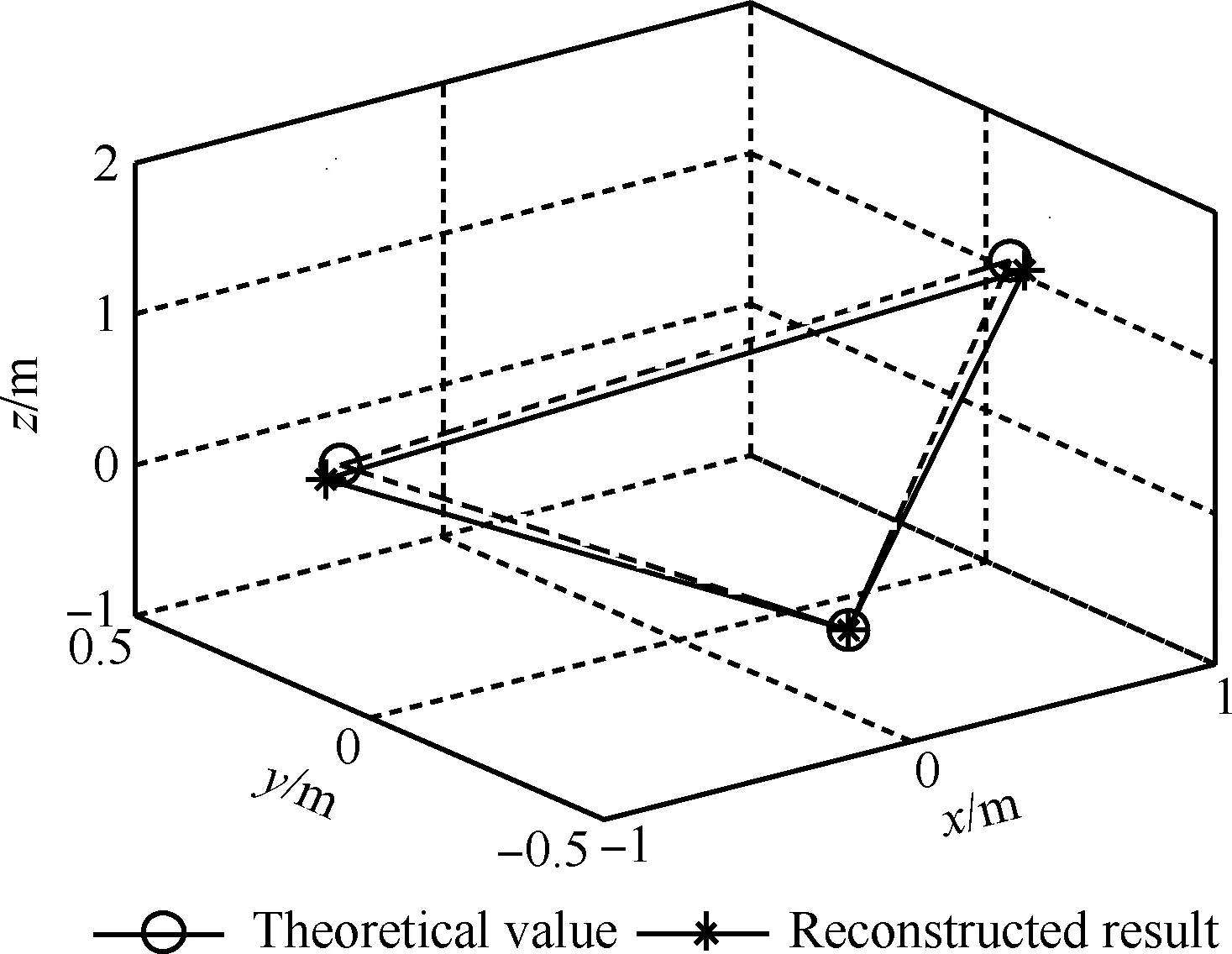
图4 三维位矢重构结果Fig.4 Reconstructed results of 3D position vectors
Table 3Precession parameters and structural parameters of target
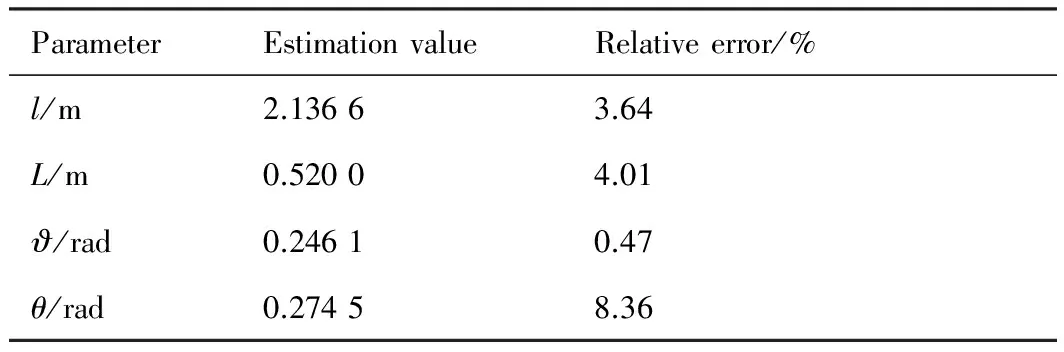
ParameterEstimationvalueRelativeerror/%l/m2.13663.64L/m0.52004.01ϑ/rad0.24610.47θ/rad0.27458.36
4.2鲁棒性分析
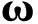
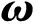
由图5可知,由于采用了散射中心关联处理及微特征及外形参数提取方法,本文较好地克服了混合体制雷达网的数据精度相差较大对参数估计的不利影响,当信噪比较低时,目标的重构精度保持在92%左右,这远高于同等仿真条件下文献[3]中的提取精度(约为76%),且与相同仿真条件下文献[9]中的提取精度相一致(仅利用了多部高分辨雷达的多视角特性),其重构参数具有很高的估计精度。
5 结 论
结合当前雷达应用的实际需求,本文利用低分辨雷达、高分辨雷达获取的微特征的关联特性实现了带有尾翼的弹头目标的微特征及外形参数提取。
1) 通过分析不同体制雷达得到的微特征之间的相互关系,构建了信号参量可分离模型,统一了不同体制雷达得到的微特征对应频率分量的参数化表达。
2) 利用散射中心关联处理方法,有效实现了混合体制雷达网中不同类型散射中心的分类,同时克服了混合体制雷达网的数据精度相差较大对数据聚类和配准的影响。
3) 在进行弹道目标微特征及外形参数提取时,利用分布式处理和加权平均相结合的方法,避免了同类型尾翼散射中心的分离问题以及数据精度相差较大的不利影响。当信噪比较低时,三维微动参数及结构参数的提取精度保持在92%左右。
4) 本文并没有分析底面边缘结构产生滑动的影响,对于弹道目标而言,其底面边缘结构对应的强散射中心会因雷达观测视角的不同而产生滑动,相应的微特征及外形参数提取方法将是下一步研究工作的重点。
[1]CHEN V C. Advances in applications of radar micro-Doppler signatures[C]//Proceeding of IEE Antenna Measurements & Application, 2014: 1-4.
[2]LIU Z, WEI X Z, LI X. Aliasing-free micro-Doppler analysis based on short-time compressed sensing[J]. IET Signal Processing, 2014, 8(2): 176-187.
[3]CHEN V C. The micro-Doppler effect in radar[M]. London: Artech House, 2011: 24-33.
[4]SMITH G E, WOODBRIDGE K, BAKER C J, et al. Multistatic micro-Doppler radar signatures of personnel targets[J]. IET Signal Processing, 2010, 4(3): 224-233.
[5]VESPE M, BAKER C, GRIFFITHS H. Radar target classification using multiple perspectives[J]. IET Radar, Sonar & Navigation, 2007, 1(4): 300-307.
[6]韩勋, 杜兰, 刘宏伟. 基于窄带雷达组网的空间锥体目标特征提取方法[J]. 电子与信息学报, 2014, 36(12): 2956-2962.
HAN X, DU L, LIU H W. Feature extraction of space cone-shaped target based on narrow-band radar network[J]. Journal of Electronics & Information Technology, 2014, 36(12): 2956-2962 (in Chinese).
[7]向道朴. 微多普勒回波模拟与微动特征提取技术研究[D]. 长沙: 国防科学技术大学, 2010: 95-111.
XIANG D P. Research on micro-Doppler echo simulation and micro-motion signature extraction technology[D]. Changsha: National University of Defense Technology, 2010: 95-111 (in Chinese).
[8]张栋, 冯存前, 贺思三, 等. 组网雷达弹道目标三维进动特征提取[J]. 西安电子科技大学学报, 2015, 42(2): 146-151.
ZHANG D, FENG C Q, HE S S, et al. Extraction of three-dimensional precession features of ballistic targets in netted radar[J]. Journal of Xidian University, 2015, 42(2): 146-151 (in Chinese).
[9]LUO Y, ZHANG Q, YUAN N, et al. Three-dimensional precession feature extraction of space targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1313-1329.
[10]AI X F, HUANG Y, ZHAO F, et al. Imaging of spinning targets via narrow-band T/R-R bistatic radars[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 362-366.
[11]PAN X Y, WANG W, LIU J, et al. Modulation effect and inverse synthetic aperture radar imaging of rotationally symmetric ballistic targets with precession[J]. IET Radar, Sonar & Navigation, 2013, 7(9):950-958.
[12]CAMP W W, JOSEPH T M, O’ DONNELL R M. Wideband radar for ballistic missile defense and range-Doppler imaging of satellites[J]. Lincoln Laboratory Journal, 2000, 2(2): 267-268.
[13]GUO K Y, SHENG X Q. Precise recognition of warhead and decoy based on components of micro-Doppler frequency curves[J]. Science China Information Sciences, 2012, 55(4): 850-856.
[14]BARHAT M. Signal detection and estimation[M]. London: Artech House, 2005: 576-580.
[15]WANG J, LEI P, SUN J P, et al. Spectral characteristics of mixed micro-Doppler time-frequency data sequences in micro-motion and inertial parameter estimation of radar targets[J]. IET Radar, Sonar & Navigation, 2014, 8(4): 275-281.
[16]SHAO C Y, DU L, HAN X. Multiple target tracking based separation of micro-Doppler signals from coning target[C]//Proceeding of IEEE Radar Conference. Piscataway, NJ: IEEE Press, 2014: 130-133.
[17]李靖卿, 冯存前, 张栋. 基于自适应视野聚类匹配的多目标分离与提取[J]. 系统工程与电子技术, 2015, 37(9): 1974-1979.
LI J Q, FENG C Q, ZHANG D. Multi-target separation and extraction based on adaptive vision cluster matching[J]. Systems Engineering and Electronics, 2015, 37(9): 1974-1979 (in Chinese).
[18]张群, 罗迎. 雷达目标微多普勒效应[M]. 北京: 国防工业出版社, 2013: 22-81.
ZHANG Q, LUO Y. Micro-Doppler effect of radar targets[M]. Beijing: National Defense Industry Press, 2013: 22-81 (in Chinese).
[19]ALEX R, ALESSANDRO L. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6): 1492-1496.
[20]李孝辉, 杨旭海, 刘娅, 等. 时间频率信号的精密测量[M]. 北京: 科学出版社, 2010: 162-180.
LI X H, YANG X H, LIU Y, et al. Precise measure of time-frequency signature[M]. Beijing: Science Press, 2010: 162-180 (in Chinese).
[21]OSSAMA A, AHMED G. Dynamic-size multiple populations genetic algorithm for multigravity-assist trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 520-529.
李靖卿男, 硕士研究生。主要研究方向: 雷达信号处理。
Tel: 029-84789420
E-mail: lijingqing_1025@126.com
冯存前男, 博士, 教授, 博士生导师。主要研究方向: 雷达信号处理、 雷达电子战新技术。
Tel: 029-84789131
E-mail: fengcunqian@sina.com
孙宏伟男, 博士, 高级工程师。主要研究方向: 雷达系统、 电子对抗技术。
E-mail: liuyanhui1999@126.com
贺思三男, 博士, 讲师。主要研究方向: 雷达信号处理、 复杂运动目标成像。
E-mail: hesisan@163.com
Micro-motion feature and shape parameters extraction based onhybrid-scheme radar network for ballistic targets
LI Jingqing1,2, FENG Cunqian1,*, SUN Hongwei2, HE Sisan1
1. Air and Missile Defense College, Air Fore Engineering University, Xi’an710051, China 2. No.93764 Unit, People’s Liberation Army of China, Baotou075000, China
Aiming at the complexity of recognition and resolution on ballistic mid-course target, a method for three-dimensional reconstruction of ballistic target based on hybrid-scheme radar network combined low-resolution radar with high-resolution radar is proposed. Based on the separable model of nonlinear signal parameter, the amplitude-phase parameters of each scattering center on the ballistic target group with empennages are calculated by nonlinear least squares estimation method. Combined with the relationship of micro-motion features between radars, various scattering centers are separated by association processing between scattering centers. Ultimately, the three-Dimensional micro-motion features and the three-Dimensional position vectors are reconstructed by utilizing both the micro-Doppler characteristics and the relative position relation of each scattering center of ballistic target, and then the precession feature and structural parameters are estimated. Simulation results validate that the reconstruction precision of three-dimensional features has been maintained at about 92% when the signal noise ratio (SNR) is 5 dB.
micro-motion feature; hybrid-scheme radar network; matching; feature extraction; ballistic target
2015-07-13; Revised: 2015-11-26; Accepted: 2016-02-29; Published online: 2016-03-0813:09
s: National Natural Science Foundation of China ( 61372166, 61501495): The Project Supported by Natural Science Basic Research Plan in Shaanxi Province of China (2014JM8308)
. Tel.: 029-84789131E-mail: fengcunqian@sina.com
2015-07-13; 退修日期: 2015-11-26; 录用日期: 2016-02-29;
时间: 2016-03-0813:09
www.cnki.net/kcms/detail/11.1929.V.20160308.1309.006.html
国家自然科学基金 (61372166, 61501495); 陕西省自然科学基础研究计划资助项目 (2014JM8308)
.Tel.: 029-84789131E-mail: fengcunqian@sina.com
10.7527/S1000-6893.2016.0054
V243.2; TN953
A
1000-6893(2016)06-1963-11
引用格式: 李靖卿, 冯存前, 孙宏伟, 等. 基于混合体制雷达网的弹道目标微特征及外形参数提取[J]. 航空学报, 2016, 37(6): 1963-1973. LI J Q, FENG C Q, SUN H W, et al. Micro-motion feature and shape parameters extraction based on hybrid-scheme radar network for ballistic targets[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1963-1973.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
URL: www.cnki.net/kcms/detail/11.1929.V.20160308.1309.006.html

