基于相似理论的星球车牵引通过性模型

黄晗， 李建桥,*， 党兆龙， 吴宝广， 邹猛

1.吉林大学 工程仿生教育部重点实验室， 长春　130025 2.中国空间技术研究院， 北京　100194



基于相似理论的星球车牵引通过性模型

黄晗1， 李建桥1,*， 党兆龙2， 吴宝广1， 邹猛1

1.吉林大学 工程仿生教育部重点实验室， 长春130025 2.中国空间技术研究院， 北京100194

深空探测车辆在星球表面巡视过程中，应避免过度沉陷，保障其可靠的通过性能具有重要意义。月球和火星表面重力加速度分别约为地球表面重力加速度的1/6和2/5，地面实现低重力环境的模拟具有一定局限性，因此基于相似理论进行轮壤相互作用系统的量纲分析，研制二分之一缩比模型车；开展缩比模型车轮壤试验，重点研究滑转条件下车轮沉陷行为和牵引特性；基于地面力学理论，结合轮壤接触应力分布的线性化方法，建立与沉陷和滑转率相关联的星球车挂钩牵引力预测模型。通过土槽试验数据对模型进行验证，结果表明该模型具有较高的准确性。能够为星球车通过性评估提供一定的理论技术基础。

星球车； 相似理论； 计算模型； 沉陷量； 模拟月壤； 深空探测

车辆行走在松软地面时，其沉陷由土壤的压实变形与滑转沉陷两部分组成。其中，车轮滑转会导致车辆行驶阻力和车轮沉陷的增加[1-2]。月球/火星表面覆盖着一层松软的粉末状月壤/火壤，星球车巡视过程中很容易出现下陷，影响其科学探测任务[3]。例如，美国的“机遇号”和“勇气号”火星车均陷入过松软沙丘中，后者最终因无法继续移动成为静止观测平台。因此，开展深空探测车辆在星球表面沉陷行为和牵引特性研究，为其前方通过性能预估、在轨巡视器地面任务支持提供基础数据和技术方法，具有重要意义[4]。

月球和火星表面的重力加速度分别约为地球表面的1/6和2/5，在地面实现低重力环境的模拟具有一定局限性。目前已有的几种低重力模拟方法包括：抛物线飞行法、悬挂法和自由落体法等，存在成本较高、控制精度要求高和低重力持续时间短等问题[5]。为在地面重力环境下，开展星球车牵引特性试验，可基于相似模型理论，通过一定比例缩小车辆结构参数，来当量于低重力对其行驶性能产生的影响[6-8]。目前，缩比模型存在无法加工制作的难题，大多数研究采用全尺寸原型样车开展牵引性能试验，这对于试验成本和场地的要求较高。文献[9]从影响车辆牵引性能的因素出发，基于相似理论推导了牵引特性的无因次全组，以待测试验土壤参数不变为约束条件，基于模型试验理论，推导了缩比牵引性能模型试验的比例因子，提出一种全尺寸的牵引性能模型试验方法。文献[10]引入相似理论对月球车的轮壤交互系统进行研究，建立了月壤-车轮交互系统的地面力学相似模型。利用室内土槽试验和颗粒流仿真对该模型试验方法进行验证，结果表明该方法对于月面重力环境下月球车牵引性能的预测，具有一定的可行性和有效性。

本文基于相似理论，进行轮壤相互作用系统的量纲分析，研制二分之一缩比模型车；开展缩比星球模型车轮壤试验，重点研究滑转条件下的车轮沉陷行为和牵引特性；基于地面力学理论，结合轮壤接触应力分布的线性化方法，建立轮壤相互作用挂钩牵引力预测模型，以期为星球车通过性评估提供一定的基础数据和理论判据。

1　轮壤相互作用模型

1.1沉陷模型

车轮行走在松软地面时，车辆沉陷由土壤的压实变形与滑转沉陷两部分组成。车辆地面力学理论中，比较常用的有Reece-Wong的沉陷计算模型[1-2]，但该模型未考虑车轮滑转对沉陷的影响。基于此，一些研究人员提出了基于滑转率的半经验沉陷模型[11-13]为

(1)

(2)

z=z0+sHp

(3)

式中：z为车轮总沉陷；z0和zs分别为车轮静沉陷和滑转沉陷；D为车轮直径；s为车轮滑转率；c1和c2为拟合系数；θ1和θm分别为车轮接近角和轮下最大应力处对应的中心角；hg为轮刺高度；Hp为土壤变形深度。近年来，随着车辆地面力学理论逐步完善，国内外学者在这方面也作了进一步的研究。

文献[12]从等效做功的角度，分析得到了车轮沉陷关于滑转率的计算模型为

(4)

与式(1)～式(3)相比，式(4)能更为准确地预测车轮沉陷，预测值与试验值的误差不超过5%。

文献[3]从土壤力学性能参数以及滑转率两个方面出发，对车轮滑转状态下沉陷量的力学关系进行分析，在适合于刚性轮静态沉陷计算模型基础上，建立了适用于滑转条件下月球车车轮的沉陷计算模型：

(5)

式中：kc和kφ分别为土壤内聚的和摩擦的模量；n为土壤的沉陷指数；b为车轮宽度；W为轮上载荷；A和B为沉陷指数n的修正系数；C和E为与滑转率s相关的系数。该模型为车辆的通过性能预测提供了新的判据。

文献[14-15]通过对滑转条件下的轮壤相互作用模型参数化分析，讨论了滑转率对传统沉陷模型的影响规律，得到沉陷指数的修正模型，为准确预测车轮滑转沉陷提供了新思路。

1.2力学模型

根据地面力学理论，基于轮下应力分布的轮上载荷W、挂钩牵引力Fd和驱动扭矩T的计算模型为[16]

(6)

(7)

(8)

式中：θ2为车轮离去角；θ为轮壤接触面上的任意角度；σ(θ)和τ(θ)分别为θ处对应的轮下法向应力和切向应力。

轮壤相互作用的力学模型中，挂钩牵引力作为模型车牵引特性的重要指标，与沉陷一起联合考虑作为星球车牵引通过性重要指标[16]。沉陷、挂钩牵引力与车轮接近角θ1和离去角θ2以及滑转率相关。式(6)～式(8)中，σ(θ)和τ(θ)中的θ1和θ2的精确测量较为困难，因此国内外学者进行了相关研究，得到了简化的轮壤关系力学计算模型。文献[17]通过轮壤作用关系的线性化推导，建立了基于车轮沉陷的挂钩牵引力模型，对在轨评估星球车通过性具有重要意义。文献[18-19]对轮下应力分布进行线性化简化，得到等效的轮壤相互作用模型，为星球车挂钩牵引力、星壤力学特性参数的实时计算提供了一定的理论基础和技术方法。但上述研究成果仅适用于单轮，因此，本文针对整车各轮不同滑转条件，开展沉陷和牵引特性试验研究，为建立适合于星球体的牵引通过性模型提供基础数据和技术方法。

2　模型车试验

2.1轮壤相互作用系统量纲分析

基于地面力学理论，轮壤相互作用系统的主要参数如表1所示。本文采用质量系统，L、M和T分别代表长度l、质量m和时间t的量纲。土壤力学性能参数中，n为无量纲参数，而土壤内聚模量kc和摩擦模量kφ的量纲中包含沉陷指数n，形式较为复杂，引入Reece修正公式可以做到无量纲化[10]，故量纲分析时只考虑土壤的内聚力c和体密度ρ；车辆行驶参数中主要考虑挂钩牵引力Fd、轮上载荷W、驱动力矩T和行驶速度v。

表1轮壤相互作用系统主要参数及其量纲

Table 1Main parameters of wheel-soil interaction system and corresponding dimensions

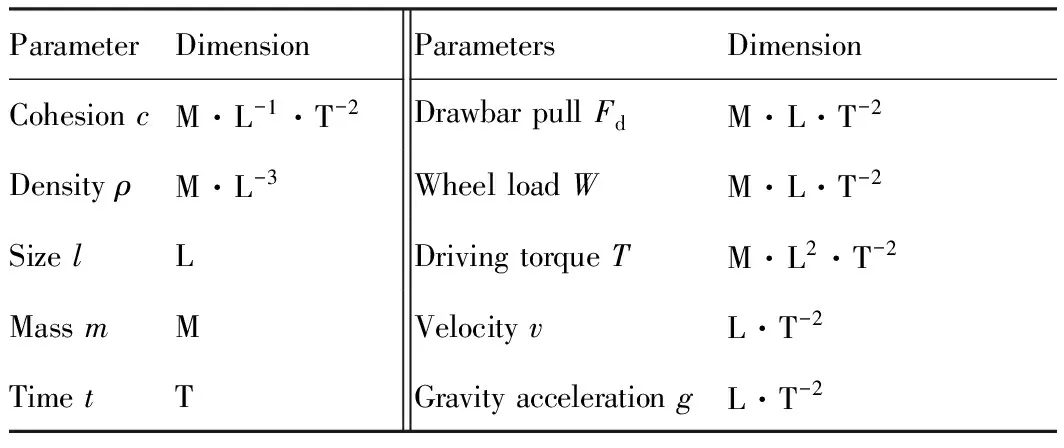
ParameterDimensionParametersDimensionCohesioncM·L-1·T-2DrawbarpullFdM·L·T-2DensityρM·L-3WheelloadWM·L·T-2SizelLDrivingtorqueTM·L2·T-2MassmMVelocityvL·T-2TimetTGravityaccelerationgL·T-2

根据Buckingham定理和相似性原理，可推导出模型和原型的相似比例尺Ki(i为轮壤相互作用系统参数)为

(9)

式中：Ki=im/ip(im为模型参数值，ip为原型参数值)；Kg为地球表面重力加速度与星球表面重力加速度比值(月球Kg=6，火星Kg=5/2)。由于土壤参数的调节较为复杂且难以控制，因此，在推导轮壤相互作用系统各参数相似比例尺时，可分土壤内聚力不变(Kc=1)和体密度不变(Kρ=1)两种情况考虑。另外，考虑到加工制作的可靠性，本研究中模型车与原型样车比例尺采用二分之一(Kl=1/2)。

综上所述，针对月球和火星表面重力加速度环境，轮壤相互作用系统各参数比例尺分别如表2(月球)和表3(火星)所示。由表2和表3可知：当Kc=1时，模型比例尺分别为Km=1/24(Kg=6)和Km=1/10(Kg=5/2)，模型相对原型车体质量较小，研制存在较大难度。因此，本研究选择Kρ=1条件下，研制二分之一缩比模型车，Km=1/8，即模型车质量为原型车的1/8。

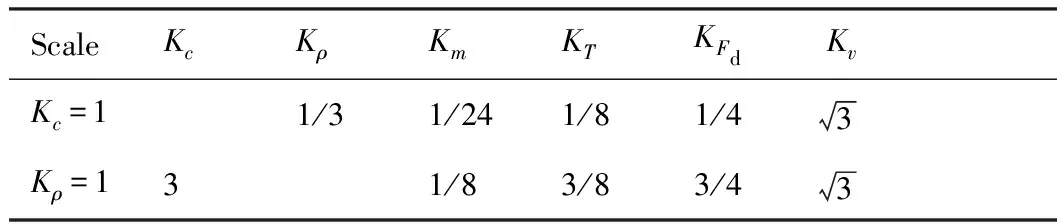
表2　相似比例尺(Kl=1/2, Kg=6)

表3　相似比例尺(Kl=1/2, Kg=5/2)

2.2设备和方法

试验采用月球车-土槽试验系统，主要包括模型车(见图1)、激光测距装置(见图2)和土槽。其中，模型车总体尺寸长、宽和高分别为750、500和220 mm，单轮的平均轮下载荷为5.6 N，相对误差波动范围为±5.5%。

1—Controller; 2—Main rocker arm; 3—Auxiliary rocker arm; 4—Drive motor; 5—Wheel; 6—Power supply; 7—Differential mechanism　图1　星球车模型Fig.1　Model of planetary rover

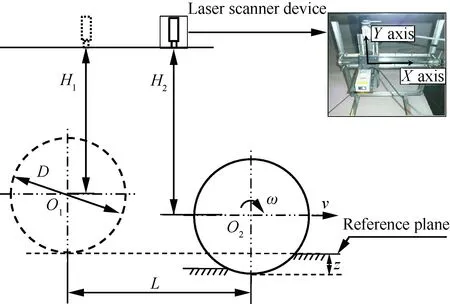
图2　非接触激光测量Fig.2　Non-contact laser measurement

模型车车体为六轮摇杆悬吊式悬架，包括主摇臂2和主摇臂3，为减轻整车质量，摇臂采用铝合金镂空结构；车轮5为筛网轮，轮面交替均匀排布有轮刺，数目为20，高度和宽度分别为5 mm和1 mm，轮径和轮宽分别为150 mm和75 mm，采用3D打印加工成型，材料为ABS树脂，具有质量轻的优点；为避免外部控制线对车辆行驶产生拖拽影响，车轮采用无线控制器1，可实现速度实时调控。驱动电机4采用步进电机，便于精确控制，最大输出转速和转矩分别为26 r/min和1.5 N·m，电源6输出电压为12 V。为避免模型车行驶过程中，质心存在较大波动，车体中部设计和安装有对称的差动机构7。

车轮沉陷量和滑转率由非接触激光测量获取，其中激光测量装置(见图2)主要由激光测距仪、二维移动框架和驱动步进电机组成，激光测距仪型号为DLS-C15，垂直测距范围为0.05～65 m，测距分辨率达到0.1 mm，X和Y方向最大测量范围分别为650 mm和500 mm[20]。图2中，O1和O2分别为车轮初始和行驶状态下的轮心位置，ω和v分别为车轮转速和水平前进速度。车轮沉陷值和滑转率通过式(10)和式(11)计算得到

z=H2-H1

(10)

(11)

式中：H1和H2分别为车轮刚接触试验介质时和行驶过程中轮心与测距仪之间的距离；L为车轮转一圈时的水平前进位移。

2.3试验条件

星球车在执行巡视探测任务时，需要根据星球表面传回的拍摄图片对就位地形进行分析和判断，从而调整星球车位姿以及进行合理的路径规划，因此星球车行驶速度一般较低，本试验中车轮行驶速度范围取为15 mm/s[21]。

试验介质采用吉林大学工程仿生教育部重点实验室研制的JLU-2型模拟月壤，主要以火山灰为原料加工配制而成，含水率小于2%，属于干性沙壤[22]。为开展对比试验，试验介质还包括一种颗粒粒径分布较为均匀的石英砂。二者物理力学性能参数如表4所示，其中，石英砂的内聚力明显较JLU-2型模拟月壤的小。为确保试验重复一致性，试验前对试验介质进行翻松和刮平操作，通过SC-900型土壤硬度计检测整备效果。本研究中模拟月壤和石英砂初始状态对应的贯入阻力最大值为600 kPa和850 kPa，贯入深度为250 mm，相对误差不超过10%。

表4　试验介质力学性能参数

3　试验结果分析

为实现模型车的不同滑转工况，本研究采用挂钩牵引力Fd控制车轮滑转率s。试验中，整车的Fd范围为0～12 N，对应s的范围为5%～95%。当s=95%时，车轮轮心位置接近试验介质基准平面，此时整车达到“陷住”的试验极限工况。

3.1沉陷

图3为模型车在模拟月壤上的各车轮沉陷随滑转率变化曲线。由图3可知，模型车前轮和中间轮的滑转率保持一致，且较后轮的滑转率大。

图3　沉陷-滑转率变化曲线(模拟月壤)Fig.3　Sinkage varying with slip ratio on simulant regolith

图3(a)为前轮和中间轮沉陷随滑转率变化曲线，沉陷随滑转率增加呈现指数增加趋势。中间轮沉陷值较前轮的小，平均减小了约43.5%。随着滑转率的增加，二者沉陷差值逐渐增大，这是由于前轮后方车辙的壅土高度随滑转率增加而增加，中间轮沿着前轮车辙前进时，其“基准面”相对升高，沉陷值则相应减小。

图3(b)为后轮沉陷-滑转率曲线，发现后轮滑转率最大值为37.4%，分析是由于试验介质经前轮和中间轮的两次压实作用后，变得密实且物理力学性能趋于稳定，滑转率不再继续增加。试验中，滑转率达到约25%后，沉陷值在9.5 mm上下波动，波动误差小于5.3%。

图4　沉陷-滑转率变化曲线(石英砂)Fig.4　Sinkage varying with slip ratio on quartz sand

模型车在石英砂上的各车轮沉陷随滑转率变化趋势与在模拟月壤上保持一致(见图4)。由图4(a)可知，当滑转率小于约30%时，中间轮沉陷量较前轮的大，随着滑转率继续增加，前轮沉陷量逐渐超过中间轮，分析是由于低滑转率条件下前轮对中间轮前方试验介质的“松土”作用大于其压实作用。由图4(b)可知，后轮滑转率和沉陷最大值分别为63.8%和11.5 mm。试验中，滑转率达到约45%后，沉陷趋于稳定，均值为11.2 mm，波动误差小于3.6%。

对比图3和图4，发现模型车各轮在模拟月壤上沉陷量总体大于在石英砂上沉陷量，主要原因在于石英砂颗粒粒径分布较均匀，且带有明显的尖锐棱角，颗粒间滑动摩擦力相对较小，咬合摩擦力起主要作用，因此相同试验条件下，沉陷量偏小。另外，由于模拟月壤的内聚力较石英砂的大，经过前轮和中间轮两次压实作用后，前者较后者更为密实，因此后轮在模拟月壤上的滑转率最大值较在石英砂上的小。

3.2挂钩牵引力

试验中，由于无法测量单个轮的挂钩牵引力值，故本文重点研究整车总挂钩牵引力和各车轮滑转率关系。不同试验介质上，车轮挂钩牵引力随滑转率变化曲线如图5所示，最大挂钩牵引力分别为12 N(模拟月壤)和11 N(石英砂)。

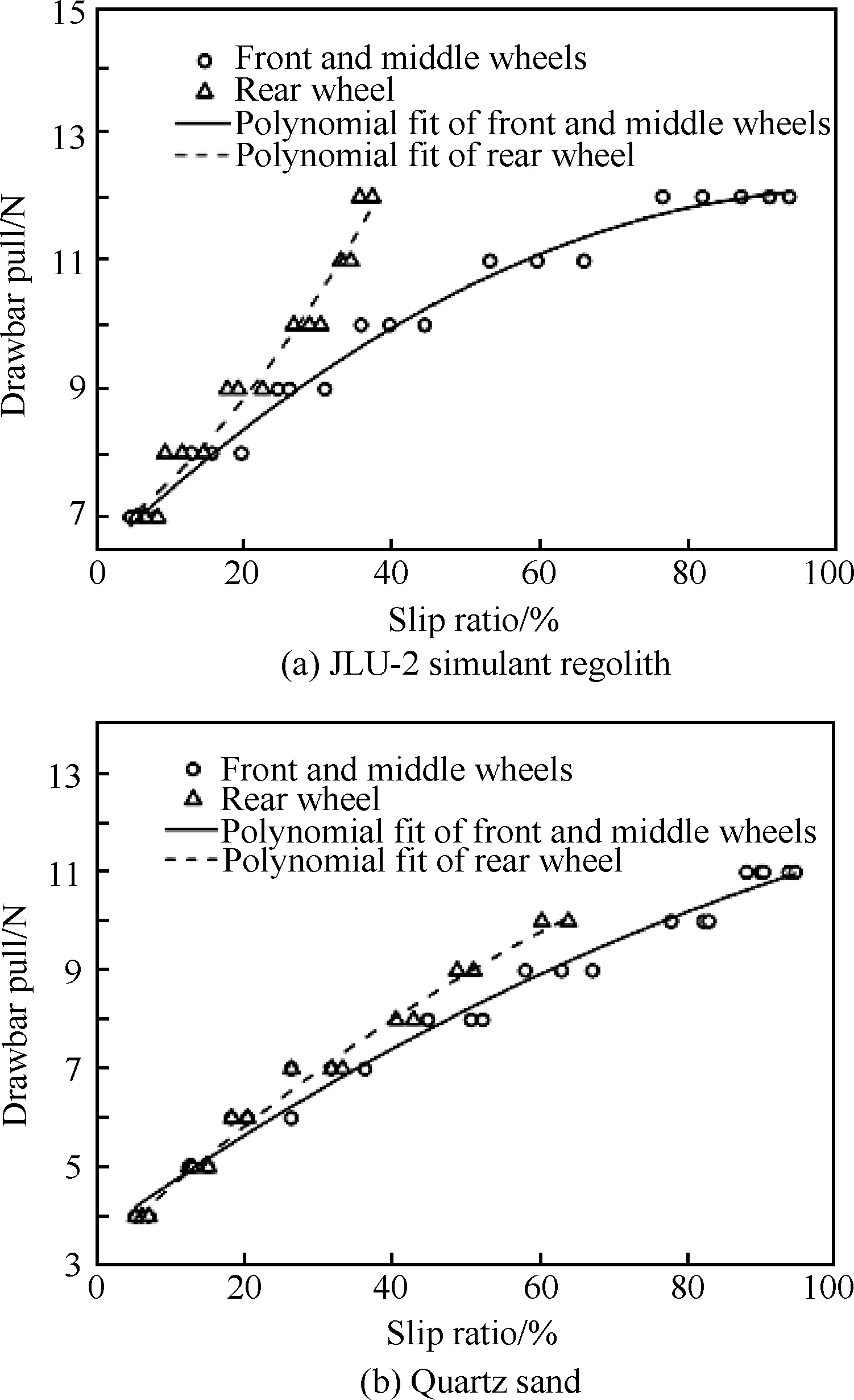
图5　挂钩牵引力-滑转率变化曲线Fig.5　Drawbar pull varying with slip ratio

由图5(a)发现，当滑转率达到40%时，前轮和中间轮挂钩牵引力提高了约42.9%，后轮则提高了71.4%，表明模拟月壤在经过前轮和中间轮两次压实作用后变得密实，使得后轮牵引性能得到提高。由图5(b)可知，模型车在石英砂上各轮牵引性能相差不明显，当滑转率达到60%时，模型车各轮挂钩牵引力均提高了约1.25倍。由以上分析可得，模型车在石英砂上挂钩牵引力随滑转率增加率较模拟月壤上大。

综上所述，模型车分别在模拟月壤和石英砂上行驶时，前者车轮沉陷总体较后者大，模型车在模拟月壤上总体牵引通过性能较在石英砂上好。不同滑转条件下，车轮压实作用导致各车轮前方土壤的密实度存在一定的差异，对后轮的沉陷和牵引特性产生了较为明显的影响，其牵引通过性能优于前轮和中间轮。

4　挂钩牵引力模型

4.1模型建立

挂钩牵引力与轮下应力分布函数相关，为简化模型计算，可对轮下应力分布函数σ(θ)和τ(θ)进行线性化处理[17-19,23]，即

(12)

(13)

得到的挂钩牵引力模型为

(14)

式中：σmax和τmax分别为轮下最大法向应力和最大切向应力；K1和K2为与θ1相关的模型参数，表达式为

(15)

本文研究中，车轮接近角θ1值小于65°(约为 1.13 rad)，K1和K2随θ1变化关系如图6所示。由图6可知，K1值随θ1变化波动较小，相对均值为 0.131 4，其平均波动误差为3.81%，故K1用其均值代替。另外，发现K2与θ1的关系存在线性关系。通过以上分析，挂钩牵引力模型可简化为

图6　模型参数与接近角θ1的关系Fig.6　Relationship between model parameters and θ1

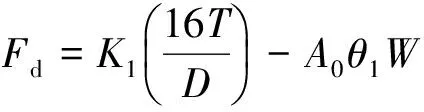
(16)

式中：A0为与θ1相关的模型拟合系数。该模型将挂钩牵引力表示为车轮驱动扭矩T、轮上载荷W、轮径D和接近角θ1的函数。其中，试验中T、W和D数值的准确获取较θ1容易。由于沉陷与车轮接近角θ1和滑转率存在相关性[23]，基于式(1)，沉陷公式可修正为

(17)

式中：B0～B2为与滑转率相关的模型拟合系数。基于车轮沉陷值和滑转率，由式(17)计算得到θ1值，从而对挂钩牵引力进行预测。综上所述，最终得到修正的挂钩牵引力模型为

(18)

式中：C0～C3为模型拟合系数，模型考虑了车轮滑转率s和滑转沉陷zs对挂钩牵引力影响。星球车结构参数(D)和负载(W)一定时，将滑转率、沉陷量和驱动扭矩值作为模型输入量对其挂钩牵引力进行预测。车轮滑转率和沉陷值可通过车辙信息间接获取[20]，驱动扭矩则可由电机驱动电流估算得到[17]。

4.2模型验证

由于模型车试验中单轮挂钩牵引力无法获取，故采用土槽单轮试验数据进行拟合得到模型式(18)中系数C0～C3的取值，如表5所示。基于相似理论，进一步通过模型式(18)计算模型车在模拟月壤上的总挂钩牵引力，模型预测值与试验值如图7所示。

试验条件下，试验值与预测值相对误差均值为8.6%，表明该模型对整车挂钩牵引力具有一定预测性。当滑转率小于65%时，预测值与试验值相对误差的均值为3.81%，且最大值不超过9.66%。当滑转率大于65%时，随着滑转率的逐渐增加，模型车的安全通过性能趋于不稳定，可能无法继续通过，属于危险工况。因此，模型对于高滑转率下的挂钩牵引力预测准确度有所下降。

表5　模型系数取值

图7　预测挂钩牵引力值与试验值比较Fig.7　Predicted and experimental values of drawbar pull

5　结　论

1) 基于相似理论，开展了轮壤相互作用系统的量纲分析，分别推导了土壤内聚力和密度参数不变情况下系统各参数比例尺，并研制出二分之一缩比模型样车。

2) 试验条件下，模型车前轮和中间轮的滑转率保持一致，但明显较后轮的大。模型车在模拟月壤上行驶时，车轮沉陷和最大挂钩牵引力均较在石英砂上的大，模型车最大挂钩牵引力分别为12 N(模拟月壤)和11 N(石英砂)。

3) 基于相似性原理和地面力学理论，结合轮壤接触应力线性化方法，建立了与沉陷和滑转率相关联的星球车挂钩牵引力预测模型,试验条件下，试验值与预测值相对误差均值为8.6%，结果表明该模型对于星球车的牵引通过性能具有一定的预测性。

[1]WONG J Y. Theory of ground vehicles[M]. Hoboken, NJ: John Wiley & Sons, 2008： 133-134．

[2]WONG J Y. Terramechanics and off-road vehicle engineering[M]. 2nd ed. Oxford: Elsevier, 2010： 84-85.

[3]金大玮, 李建桥, 党兆龙, 等. 滑转条件下月球车轮沉陷模型研究[J]. 航空学报, 2013, 34(5): 1215-1221.

JIN D W, LI J Q, DANG Z L, et al. Study on model for sinkage of lunar rover wheel under the condition of slip[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1215-1221 (in Chinese).

[4]崔平远, 徐瑞, 朱圣英, 等. 深空探测器自主技术发展现状与趋势[J]. 航空学报, 2014, 35(1): 13-28.

CUI P Y, XU R, ZHU S Y, et al. State of the art and development trends of on-board autonomy technology for deep space explorer[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 13-28 (in Chinese).

[5]徐文福, 梁斌, 李成, 等. 空间机器人微重力模拟实验系统研究综述[J]. 机器人, 2009, 31(1): 88-96.

XU W F, LIANG B, LI C, et al. A review on simulated micro-gravity experiment systems of space robot[J]. Robot, 2009, 31(1): 88-96 (in Chinese).

[6]KURODA Y, TESHIMA T, SATO Y, et al. Mobility performance evaluation of planetary rover with similarity model experiment[C]//2004 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2004: 2098-2103.

[7]WONG J Y. Predicting the performances of rigid rover wheels on extraterrestrial surfaces based on test results obtained on earth[J]. Journal of Terramechanics, 2012, 49(1): 49-61.

[8]WONG J Y, KOBAYASHI T. Further study of the method of approach to testing the performance of extraterrestrial rovers/rover wheels on earth[J]. Journal of Terramechanics, 2012 (in press).

[9]江磊, 郭建娟, 陈传海. 基于相似理论的月球车牵引性能模型试验[J]. 中国机械工程, 2009, 23(20): 2828-2831.

JIANG L, GUO J J, CHEN C H. Scaling model experiment of lunar rover’s mobility performance based on similarity model theory[J]. China Mechanical Engineering, 2009, 23(20): 2828-2831 (in Chinese).

[10]李萌, 高峰, 孙鹏, 等. 基于相似理论的月球车月面牵引性能预测[J]. 北京航空航天大学学报, 2013, 39(2): 230-234.

LI M, GAO F, SUN P, et al. Prediction of lunar rover's moon tractive performance based on similitude theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 230-234 (in Chinese).

[11]REINA G, OJEDA L, MILELLA A, et al. Wheel slippage and sinkage detection for planetary rovers[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(2): 185-195.

[12]LYASKO M. Slip sinkage effect in soil-vehicle mechanics[J]. Journal of Terramechanics, 2010, 47(1): 21-31.

[13]李建桥, 黄晗, 王颖, 等. 松软地面机器系统研究进展[J]. 农业机械学报, 2015, 46(5): 130-145.

LI J Q, HUANG H, WANG Y, et al. Development on research of soft-terrain machine systems[J].Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 130-145 (in Chinese).

[14]GAO H B, GUO J L, DING L, et al. Longitudinal skid model for wheels of planetary exploration rovers based on terramechanics[J]. Journal of Terramechanics, 2013, 50(5): 327-343.

[15]DING L, GAO H B, DENG Z Q, et al. New perspective on characterizing pressure-sinkage relationship of terrains for estimating interaction mechanics[J]. Journal of Terramechanics, 2014, 52(2): 57-76.

[16]TAHERI S, SANDU C, TAHERI S, et al. A technical survey on terramechanics models for tire-terrain interaction used in modeling and simulation of wheeled vehicles[J]. Journal of Terramechanics, 2015, 57(1): 1-22.

[17]丁亮亮, 肖杰, 宗魏, 等. 与沉陷相关联的星球车挂钩牵引力模型研究[J]. 农业机械学报, 2014, 45(12): 37-42.

DING L L, XIAO J, ZONG W, et al. Drawbar pull model of planetary rover associated with subsidence[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12): 37-42 (in Chinese).

[18]IAGNEMMA K, KANG S, SHIBLY H, et al. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers[J]. IEEE Transactions on Robotics, 2004, 20(5): 921-927.

[19]SHIBLY H, IAGNEMMA K, DUBOWSKY S. An equivalent soil mechanics formulation for rigid wheels in deformable terrain, with application to planetary exploration rovers[J]. Journal of Terramechanics, 2005, 42(1): 1-13.

[20]王洋, 李建桥, 党兆龙, 等. 松散地面上车辙表面的非接触式激光测量[J]. 农业机械学报, 2013, 44(7): 264-268.

WANG Y, LI J Q, DANG Z L, et al. Non-contact laser measurement of rutting surface on loose ground[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(7): 264-268 (in Chinese).

[21]DING L, GAO H B, DENG Z Q, et al. Experimental study and analysis on driving wheels’ performance for planetary exploration rovers moving in deformable soil[J]. Journal of Terramechanics, 2011, 48(1): 27-45.

[22]邹猛, 李建桥, 李因武, 等. 刚性轮-月壤相互作用预测模型及试验研究[J]. 农业工程学报, 2007, 23(12): 119-123.

ZOU M, LI J Q, LI Y W, et al. Prediction model and experimental study on the interaction of rigid wheel and lunar soil[J]. Chinese Society for Agricultural Machinery, 2007, 23(12): 119-123 (in Chinese).

[23]IIZUKA K, SATO Y, KURODA Y, et al. Experimental study of wheeled forms for lunar rover on slope terrain[C]//9th IEEE International Workshop on Advanced Motion Control. Piscataway, NJ: IEEE Press, 2006: 266-271.

黄晗男， 博士研究生。主要研究方向： 车辆地面力学。

E-mail: huanghan452012@163.com

李建桥男， 博士， 教授， 博士生导师。主要研究方向： 车辆地面力学。

Tel: 0431-85095575

E-mail: jqli@jlu.edu.cn

Planetary rover’s tractive performance model based onsimilarity theory

HUANG Han1, LI Jianqiao1,*, DANG Zhaolong2, WU Baoguang1, ZOU Meng1

1. Key Laboratory of Bionic Engineering (Ministry of Education), Jilin University, Changchun130025, China 2. China Academy of Space Technolegy, Beijing100194, China

It is important to ensure reliable mobility performance and avoid excessive sinkage for planetary rover. Gravity acceleration on the moon and mars is about one-sixth and two-fifths of the earth, respectively; however, there are certain limitations to simulate low gravity environment on the earth. Therefore, based on similarity principle and terramechanics theory, we present a dimensional analysis on wheel-soil system. A scaling planetary rover has been developed, which is used for eliminating the equivalent influence of the low gravity in the ground experiments. Soil bin tests of the planetary rover are conducted on two different terrains, and the sinkage and tractive characteristics of planetary model rover have also been analyzed. By combining the linearization approach on contact stress distribution between wheel and soil interface, a simplified drawbar pull model is established, which is related to the wheel sinkage and slip ratio. The model is validated through the soil bin testing data and results indicate that the proposed model has a higher accuracy in the mobility performance assessment, including wheel sinkage and drawbar pull.

planetary rover; similarity theory; calculation model; sinkage; simulant regolith; deep space exploration

2015-06-09； Revised： 2015-07-24； Accepted： 2015-07-25； Published online： 2015-08-0515：21

National Natural Science Foundation of China (51375199)

. Tel.： 0431-85095575E-mail: jqli@jlu.edu.cn

2015-06-09； 退修日期： 2015-07-24； 录用日期： 2015-07-25；

时间： 2015-08-0515：21

www.cnki.net/kcms/detail/11.1929.V.20150805.1521.003.html

国家自然科学基金 (51375199)

.Tel.： 0431-85095575E-mail: jqli@jlu.edu.cn

10.7527/S1000-6893.2015.0217

V476.3

A

1000-6893(2016)06-1974-09

引用格式： 黄晗， 李建桥， 党兆龙， 等． 基于相似理论的星球车牵引通过性模型[J]． 航空学报, 2016, 37(6): 1974-1982. HUANG H, LI J Q, DANG Z L, et al. Planetary rover’s tractive performance model based on similarity theory[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1974-1982.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20150805.1521.003.html