基于多目标差分进化算法的海上雷达部署优化的仿真分析

王君

（1.中国电子科学研究院，北京100041；2.电子科技大学，成都　611731）

基于多目标差分进化算法的海上雷达部署优化的仿真分析

王君1，2

（1.中国电子科学研究院，北京100041；2.电子科技大学，成都611731）

以最大化雷达组网静态覆盖能力与动态探测能力为优化目标，提出一种基于多目标差分进化算法的解决方案，并进行仿真实验。将优化部署的仿真结果与随机部署的仿真结果进行对比，对比结果表明，基于差分进化算法的部署优化方案具有较快的收敛速度，有效提高雷达组网的静态覆盖能力以及动态探测能力。

优化部署；海上雷达；差分进化算法；多目标优化

0　引言

雷达组网作为当前国内外在作战中广泛采用的反侦察、反干扰、反摧毁、反隐身技术措施［1］。雷达部署优化作为雷达组网系统研究的重要部分，是提高雷达组网作战效能的前提和基础。目前雷达组网优化部署研究采用的方法涉及遗传算法、粒子群算法、模拟退化算法等［1-6］以及传统的枚举法等。

本文将着眼于海上雷达组网的部署优化问题，并基于差分进化算法，从雷达组网的静态覆盖能力与动态探测能力两方面入手，建立相应的问题模型，做仿真验证。将部署优化的仿真结果与随机部署的仿真结果进行对比，进一步说明算法的有效性。

1　多目标海上雷达部署优化问题的基本描述

本文中，假定海上雷达监测的目标为海上目标，则监测区域可降维成二维平面。监测区域A在横轴与纵轴方向步长均为1被离散化为M个栅格，可知每个栅格面积为1。

雷达在探测的过程中会受到噪声、天气条件等因素的干扰，所以雷达的作用距离是一个统计值。通常会讲，当虚警概率（如10-5）和检测概率（如80%）给定时，某一型雷达作用距离为多大［7］，而不是简单给出某一型雷达的作用距离。

在此意义下的雷达探测距离方程［7］可表示为：

其中，RPd为一定条件下雷达的探测距离，Pt表示雷达的发射功率，Gt、Gr分别表示雷达发射天线与接收天线增益，σ为目标的雷达散射截面积（RCS），λ为雷达的工作波长，（SNR）Pd为信噪比，k为玻尔兹曼常数（1.38× 10-23）J/K），Bn为接收机噪声带宽。

本文中，假设雷达组网中所有部署的雷达型号一致，且均为x波段圆周扫描雷达，雷达探测半径为r。

1.1海上雷达组网的静态覆盖能力模型

在监测区域A上部署的雷达节点ni，其坐标为（xi，yi）。监测区域A上的栅格点pj，其坐标为（xj，yj）。则栅格点pj到雷达节点ni的欧氏距离为：

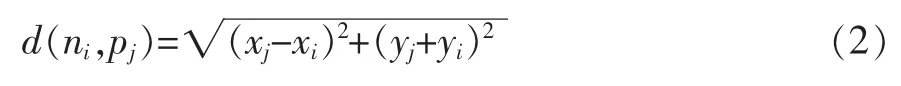
本文建立了节点布尔覆盖模型［8］，即当存在雷达节点ni，使得栅格点pj到其的距离d（ni，pj）小于雷达的探测半径r时，则认为该栅格点被覆盖，布尔覆盖模型可表示为：

则海上雷达组网的静态覆盖率可被定义为被雷达覆盖的监测面积与总面积的比值，部署优化的目标之一则是最大化雷达组网的静态覆盖率，即：

1.2海上雷达组网的动态探测能力模型

如上文提到的，雷达探测事件具有一定的概率特性。如果在一定范围内的监测区域内，某些栅格点距离一台或多台雷达较近，则相应地被探测到的概率就较大；相反，如果某些栅格点距离监测区域内的所有雷达都较远，则相应被探测到的概率就会较小，有可能成为探测盲区。

而上述布尔覆盖模型只简单反映了栅格点是否可以被覆盖的特性，无法反映探测事件的不确定性，故引入文献［9］中雷达在不同距离处的检测概率计算模型：

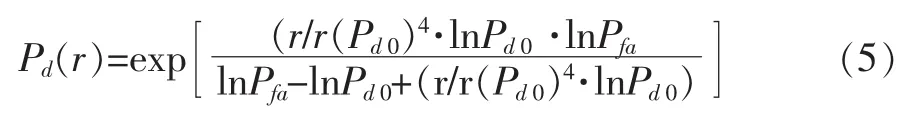
式中，r（Pd0）表示在给定检测概率为Pd0时雷达的最大探测范围，r表示雷达的探测距离。该模型详细的描述了雷达的虚警概率和雷达的最大探测范围对雷达不同距离上的探测概率会产生定量影响。

根据上述的检测概率计算模型，给定虚警概率Pfa以及约束检测概率Pd0，可计算得出栅格点pj被雷达节点ni的检测到的概率为Pd（ni，pj），则栅格点pj被K部雷达协同检测到的概率为（在这里，假设每个雷达探测事件相互独立）：

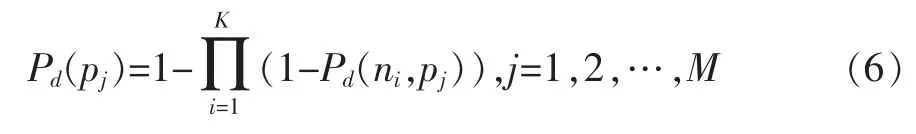
则海上雷达组网的动态探测能力可由栅格点被多部雷达协同检测概率来描述，部署优化的目标之一则是最大化雷达组网的动态探测概率，即：

1.3多目标问题描述

多目标优化问题是指在满足一定的约束条件下，同时对多个互相冲突的目标进行优化，最终求得问题的最优或次优解。

对于这样的多目标问题，一般要把各个子目标函数统一转换为最小值优化问题，一般的数学模型为：

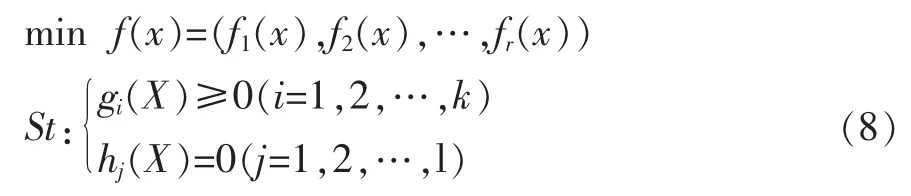
式中：r是待优化目标的个数，多目标优化的目标即在X=（x1，x2，…，xn）满足一定约束条件下，求f（x）的最优值。

对于雷达来讲，静态覆盖能力与动态探测能力的刻画存在一定的矛盾点。静态覆盖能力指的是雷达组网尽可能覆盖大的面积，而动态探测能力则希望可以做到雷达组网对监测地区的重复覆盖，以提高监测地区的检测率，故在优化部署过程中，要对两方面进行权衡。本文中，需要优化的目标函数由两部分组成：

多目标优化问题因为其复杂性，通常情况下不存在唯一的全局最优解，而是一组优化域边界上的解，这组解被称为Pareto解，即非劣解。

本文将基于差分进化的思想设计海上雷达部署优化算法，获取部署问题的Pareto解，进而确定雷达组网的部署位置。

2　多目标差分进化算法

差分进化算法是由Rainer Storn和Keneth Price 1995年提出的，旨在解决chebyshev多项式问题［10］，后经多项研究发现，差分进化算法也可作为解决复杂优化问题的有效技术。差分进化算法作为一种基于群体差异的启发式随机搜索算法，采用实数编码、基于差分的简单变异操作和一对一的竞争策略，具有原理简单、受控参数少、鲁棒性强等特点。其操作过程分为：初始化种群、变异操作、交叉操作以及选择操作4个部分。

2.1约束条件

根据本文所研究问题的实际情况，对于海上雷达部署问题做以下假设：

（1）本文采用二维坐标进行实数编码，故假设监测区域A为矩形区域；

（2）待部署雷达型号均为X波段圆周扫描雷达（X波段雷达可以很好的利用海上大气波导效应［11］）且雷达的性能参数以及待部署数量已知；

（3）假设各个雷达系统中各设备之间能够良好连接。

2.2多目标差分进化算法的关键操作

令xi（t）是第g代的第i条染色体，则：

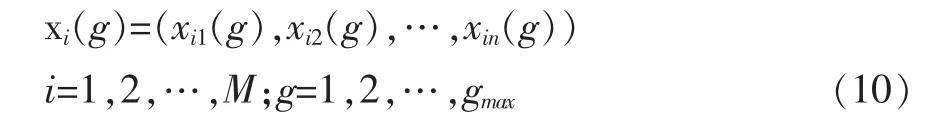
其中，n是染色体的长度，M为群体规模，gmax是最大的进化代数［13］。本文中，变量为海上雷达的部署位置，用坐标（x，y）标识，假设部署的雷达数量为5，则n= 2×5=10，编码方式如图1所示。

图1　染色体编码方式

（1）初始化种群

在n维空间里随机产生满足约束条件的M条染色体：

（2）变异操作

差分进化算法通过差分策略进行变异操作，变异成分为父代（第g代）的差分向量。在父代群体中随机选取3个个体变量（染色体）xp1、xp2、xp3且i≠p1≠p2≠p3，则常见的差分策略定义为：

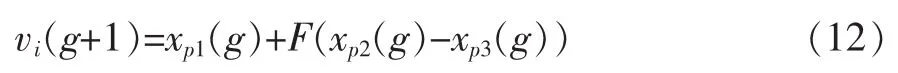
式中：xi（g）表示第g代种群中的第i个个体（染色体）。缩放因子F的取值会影响算法的性能，若取值过大会使得算法收敛速度慢，但若取值过小会导致种群多样性降低，算法易陷入局部最优的窘境［12］。

在变异过程中，还需要判定变异后的染色体的基因是否满足约束条件，若不满足约束条件，则变异后染色体基因会基于约束条件随机重新生成。

（3）交叉操作

差分进化算法中的交叉操作是为了通过目标向量xi（g）与变异向量xi（g+1）的结合来提高种群的多样性，具体操作如下：

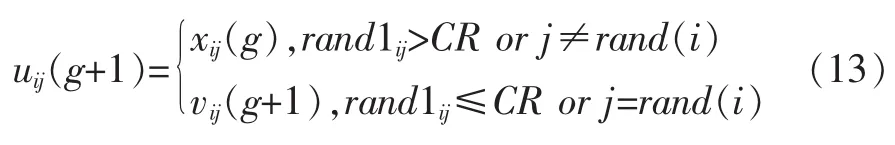
其中，CR为交叉概率，CR∈［0，1］，rand1ij是在［0，1］之间的随机小数，rand（i）表示［1，n］的随?机整数。由此保证ui（g+1）至少从vi（g+1）中获得一个分量，以产生新的个体。本文基于权衡种群的搜索能力和收敛速度［14］的角度，取CR=0.6。

（4）选择操作

根据适应度函数f对种群进行选择。通过比较目标向量与交叉变异产生的新向量的适应度函数，来决定哪个向量可以成为下一代成员：

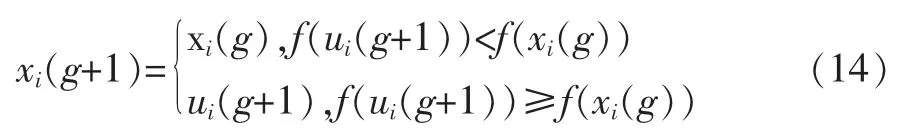
适应度函数的选取与目标函数相关，本文基于Pareto弱支配理论对个体的适应度进行评估选择。

重复执行（2）至（4）的操作，直至达到最大的进化代数gmax。

2.3多目标差分进化算法实现步骤

在培养学生自主学习能力的过程中，除了要更好地发挥学生的主体作用外，更为重要的就是要发挥教师的引导作用，改变传统以灌输式为主的教学方法，通过教师的有效引导，强化学生的自我意识和自主学习意识。比如笔者在培养学生自主学习能力的过程中，将布置式学习、探究式学习与学生自学进行了有效结合，使学生通过不同的引导方式，强化自身的主动性和创造性。再比如笔者还高度重视将课堂交给学生，但笔者更加重视对学生的引导，比如通过互动教学，将学生分成多个小组，在传授基础知识后，使学生之间能够进行合作学习，并且对各个小组在互动之后形成的成果进行总结和分析，各个小组、所有学生都能够吸收各自的互动学习成果，取得了很好的成效。

（1）初始化差分进化算法常量、待部署雷达数量、雷达相关参数（雷达探测半径、虚警概率、检测概率）等。

（2）将迭代次数置0，初始化种群个体。

（3）通过交叉变异操作，生成变异个体vi（g+1）以及生成个体uij（g+1）。

（4）进行选择操作，根据目标函数重新计算个体的适应度值并进行比较，选择相应的个体作为下一代。

（5）判断迭代次数是否达到最大值，达到最大值则继续执行步骤（6），反之则返回步骤（3）进行循环迭代。

（6）在最终得到的种群中，选择适应度函数值最大的一个个体，作为该问题的解输出。

3　仿真及结果分析

3.1仿真参数设置

仿真实验参数如表1所示：

表1　仿真参数表

3.2差分进化算法优化结果

图 2、图 3是随着迭代次数的增加，种群中Pareto解对应的目标函数f1、f2的均值变换趋势图。横轴为迭代次数，纵轴为目标函数每一代的均值。通过图中曲线可以看出，随着迭代次数的不断增加，目标函数值趋近于收敛，且在迭代初期目标函数值上升的很快。

图2　目标函数f1变化趋势图　

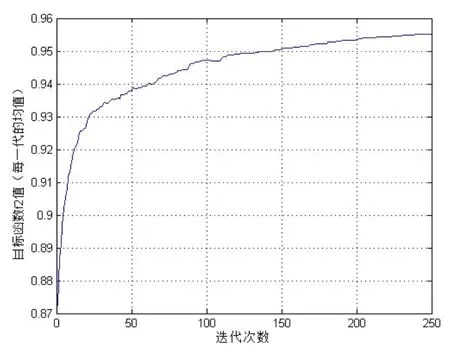
图3　目标函数f2变化趋势图

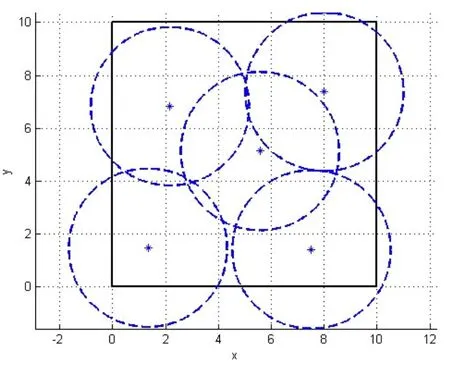
图4　优化部署结果示意图（max f1）　

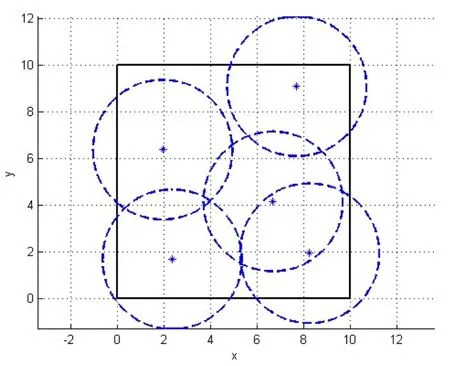
图5优化部署结果示意图（maxf2）

图4、图5为优化部署结果示意图，其中*代表雷达的部署位置，虚线圆圈为相应雷达的探测区域，实线矩形框代表监测区域。在最后一代种群中，选取目标函数f1值最大的一个个体，作为优化部署的一种方案，即为图4所示；相应的，选取目标函数f2值最大的一个个体，作为优化部署的另一种方案，即为图5所示。

3.3仿真结果对比分析

本文将基于差分进化算法的优化部署方案与随机部署方案的仿真结果进行对比分析，如表2所示，其中随机部署方案为进行多次随机部署，将得到的目标函数值取均值：

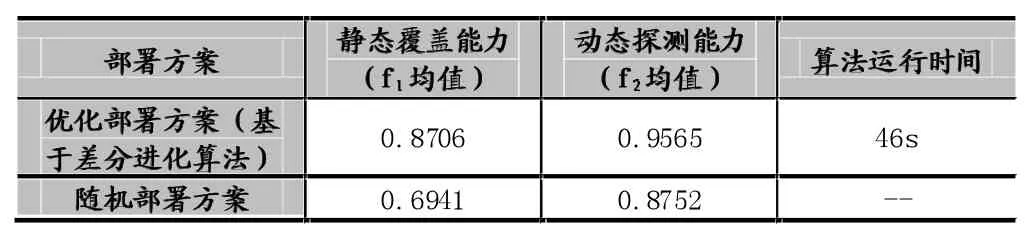
表2　优化部署方案与随机部署方案对比

从可以看出，基于差分进化算法的优化部署方案无论在静态覆盖能力方面还是动态探测能力方面均优于随机部署方案，且优化算法的运行时间很短。由表2可知，差分进化算法可以在较短时间内得到一个相对优化的部署方案。

4　结语

本文建立了以最大化雷达组网的静态覆盖能力、最大化雷达组网的动态探测能力为目标的多目标优化问题模型，并相应地提出了解决该问题的差分进化算法。仿真结果表明，本文提出的求解机制可以有效提高雷达组网的静态覆盖能力以及动态探测能力，且算法具有较快的收敛速度，可以在较短时间内得到一个相对优化的解决方案。该方法已经在某仿真系统工作中得到应用。

［1］潘伟.基于自适应遗传算法的雷达组网优化部署［J］.电子信息对抗技术，2013（4）.

［2］张远，方青，曲成华.基于遗传算法的组网雷达优化部署［J］.雷达科学与技术，2014（1）.

［3］宋佳庆，张峰，关永胜，冯占林，张晓玲.基于最优作战效能的雷达部署优化问题研究［J］.中国电子科学研究院学报，2015（8）.

［4］张培珍，杨根源，武志东，徐圣良，刘志成.模拟退火算法在雷达网优化部署中的应用［J］.现代防御技术，2010（6）.

［5］杨翠蓉，王明哲，龚浩华，倪枫.改进粒子群算法在雷达网优化部署中的应用［J］.计算机应用研究，2010（9）.

［6］张冰冰.复杂电磁环境下雷达组网优化方法研究与模拟系统设计［D］.沈阳理工大学：沈阳理工大学，2014.

［7］丁鹭飞，耿富录.雷达原理［M］.西安电子科技大学出版社，2006.

［8］李明，石为人.基于差分进化的多目标异构传感器网络节点部署机制［J］.仪器仪表学报，2010，08.

［9］郭正新，江晶.一种不同距离的雷达检测概率计算模型［J］.空军雷达学院学报.2003（04）

［10］Rainer Storn，Kenneth Price.Differential Evolution-A Simple and Efficient Heuristic for global Optimization over Continuous Spaces［J］1997，Journal of Global Optimization（4）：341-359.

［11］周文瑜 焦培南等编.超视距雷达技术［M］.北京：电子工业出版社，2008.

［12］ABBASS H A.The Self-Adaptive Pareto Differential Evolution Algorithm［C］.Proc.Congr.Evolut.Comput，Honolulu，H I，2002：831-836［20］.

［13］李高扬，吴育华，刘明广.基于差异演化算法的网络计划多目标优化［J］.中国工程科学，2006，06.

［14］GM Perle R，Mllersd，Koumoutsakosp.Aparameter Study for Differential Evolution［C］.Advances in Inteligent Systems，Fuzzy Systems，Evolutionary Computation.A.Grmela and N.E.Mastorakis，Eds.Interlaken，Switzerland，2002：293-298.

Optimal Deployment；Maritime Radar；Differential Evolution Algorithm；Multi-Objective Optimization

Simulation Analysis of the Deployment Optimization in Maritime Radar Based on Multi-Objective Differential Evolution Algorithm

WANG Jun
（1.China Academy of Electronics and Information Technology，Beijing 100041；2.University of Electronic Science and Technology of China，Chengdu 611731）

Aiming at the objectives of maximizing the abilities of static coverage and dynamic detection of radar network，proposes and simulates a solution based on the multi-objective differential evolution algorithm.Through comparing the simulation result of optimal deployment with that of random deployment，it is found that the optimal deployment，which is based on differential evolution algorithm，has a faster convergence rate and is effective in improving the static coverage and dynamic detection of radar network.

王君（1992-），女，河北沧州，在读硕士研究生，研究方向电子信息系统建模与仿真

2016-08-26

2016-10-20