波动率偏斜与风险中性偏度能预测尾部风险吗

陈　蓉， 林秀雀

(厦门大学金融系， 厦门 361005)



波动率偏斜与风险中性偏度能预测尾部风险吗

陈蓉， 林秀雀

(厦门大学金融系， 厦门 361005)

论文从S&P 500指数期权数据中提取出波动率偏斜与风险中性偏度指标，采用Logistic模型研究了波动率偏斜/风险中性偏度是否对未来真实的市场尾部风险具有预测力.结果发现，波动率偏斜/风险中性偏度仅含有未来市场尾部风险的一定信息，但并不能准确预测未来市场尾部风险发生的状态.相反，波动率偏斜/风险中性偏度与投资者情绪指标显著相关.

波动率偏斜； 风险中性偏度； 市场尾部风险； 投资者情绪

0　引　言

以1987年股灾为界，股票期权市场的隐含波动率曲线从原先的波动率微笑(volatility smile)转变为波动率偏斜(volatility skew)*Rubinstein等发现S&P500指数期权的隐含波动率曲线从1987年股灾前的“波动率微笑”转变成股灾后的“波动率偏斜”.所谓“波动率微笑”是指隐含波动率在平价期权处最低，在左右两尾实值和虚值期权处较高且比较对称；“波动率偏斜”是指隐含波动率是期权执行价格和(或)在值程度的递减函数，隐含波动率曲线呈向右下方倾斜的形态，左尾的波动率远大于右尾..Rubinstein[1]等最早指出了这一点.在他们之后，许多论文研究了这一持续存在的市场现象.波动率偏斜究竟意味着什么，迄今的主要观点有二：1)波动率偏斜意味着市场投资者认为左尾事件(即暴跌)发生的概率远大于右尾事件(即暴涨)发生的概率，在Bates[2,3]和Pan[4]等经典论文之后，这一观点几乎已经为大多数人所接受；2)波动率偏斜的产生可能还源于市场摩擦和市场微观结构等因素导致的市场期权定价偏误，持此观点的包括Bollen和Whaley[5]的“套利限制”论、Evans等[6]的“卖空成本”论和Garleanu等[7]的“净需求压力”论等.

本文试图对第一个观点进行研究.由于在图形上，波动率偏斜的形态意味着市场隐含的左尾(暴跌)概率大于右尾(暴涨)概率，因此第一个观点是很容易被理解和接受的.由此，人们很容易进一步将其解读为“波动率偏斜或可用于预测未来的暴跌(左尾)风险”.这一想法非常具有吸引力.准确预测未来的市场价格波动，特别是暴涨暴跌的尾部风险*市场尾部风险(tail risk)的精确定义有不同的表达方式，但其内涵却是明晰的：市场价格在短期内的大幅波动，包括市场暴跌(market crash或black swan)和市场暴涨(spike upward).，是投资者梦寐以求的能力，亦是金融研究者孜孜不倦的努力方向.如果真能运用期权市场的波动率偏斜信息对未来的暴跌风险加以预期，就将在“黑天鹅事件”的极端风险管理方向上迈进一大步.

已有不少学者在这方面进行了一些尝试.其中大部分是针对个股进行的横截面实证研究，研究者们运用不同的波动率偏斜测度指标，均发现个股期权市场上的波动率偏斜对未来收益率具有显著的预测力；但有趣的是，其预测方向并不一致，例如Xing等[8]发现波动率偏斜与个股未来收益率呈显著正相关，即负偏越严重，未来收益越低，而Conrad等[9]、Bali和Hovakimian[10]和Yan[11]却发现波动率偏斜与个股未来收益显著负相关.针对股指期权的研究则相对较少，较为典型的是Dokan等[12]从S&P100指数期权数据中得出结论，认为波动率偏斜的确包含对市场尾部风险的预测信息.

本文的研究主要出于以下考虑：首先，上述大部分研究实际上仅仅证实了波动率偏斜与未来收益率显著相关，直接证实波动率偏斜与未来尾部风险相关性的文献仍较少，而对尾部风险进行细分，考察波动率偏斜预测准确性的研究则至今未见；其次，期权市场价格是全体参与者整体信念和预期的综合体现，其中隐含的波动率偏斜可以视为全体投资者对未来尾部风险的平均预期，但这一预期究竟是准确的理性预期，还是受情绪影响的非理性预期？这一点迄今尚未有人进行过研究；第三，现有的大部分研究是针对个股横截面进行的，针对股指期权的研究则相对较少.因此本文的研究主题，确定为考察全世界最活跃和最成熟的期权产品之一——美国S&P500指数期权价格中隐含的波动率偏斜，是否对未来股指的尾部风险具有现实的预测能力.

基于上述目标，本文的基本研究思路如下：1)由于是针对股指和尾部风险进行的研究，而非研究个股和收益率的高低，故不采用个股研究中普遍使用的构造组合、控制其他因子影响、计算超额收益率等方法，而借鉴Doran等[12]用股指收益率的历史分位点来度量尾部风险，并用Logistic模型来直接考察某交易日的期权隐含波动率偏斜是否对未来尾部风险的发生具有预测性；2)由于不同论文使用不同的波动率偏斜指标得到了不同的结论，本文同时引入不同计算方式的波动率曲线斜率和无模型风险中性偏度(model-free risk neutral skewness)*所谓风险中性偏度，是指期权价格中隐含的资产价格未来分布的偏度(在风险中性测度下)，可运用期权价格倒求得到.不少学者认为风险中性偏度与波动率偏斜反映了相同或相关度很高的信息，如Bahra[13]和Dennis和Mayhew [14]等.因此，本文引入风险中性偏度，作为波动率偏斜的补充测度指标.共4个指标来考察它们对尾部风险的预测效果，以使结果更具有一般性；3)与Doran等[12]不同，本文对市场尾部风险进行详细分类并加以考察，结果发现这一工作意义重大，使得研究结论发生重要变化；4)与Doran等[12]不同，在考察完尾部风险预测效果之后，由于发现预测不准确，本文考虑了非理性预期的可能性，而投资者情绪可以视为非理性的体现指标，因此进一步对波动率偏斜/风险中性偏度与投资者情绪之间的关系进行了研究，对尾部风险预测部分的研究结论形成重要补充，得到了与他们全然不同的结论.

总之，本文从S&P 500指数期权数据中估计出无模型风险中性偏度和波动率偏斜的不同测度指标，对市场尾部风险进行了细分，研究了期权隐含波动率偏斜和风险中性偏度是否真的对未来的尾部风险具有预测力；然后构造投资者情绪的综合指数，研究了波动率偏斜/风险中性偏度与投资者情绪之间的关系.结果发现，尽管与不少文献相似，本文也证实了波动率偏斜和风险中性偏度的确含有未来市场尾部风险的信息，但一旦如本文这样对上下尾风险进行细致划分，波动率偏斜和风险中性偏度对未来市场尾部风险的预测能力就显著下降了；相反，本文发现，波动率偏斜和风险中性偏度却与投资者的情绪显著相关.也就是说，如同CBOE推出的VIX指数被称为波动的“恐慌指数”一样，波动率偏斜以及CBOE推出的SKEW指数可能更多反映的是投资者情绪，却难以成为未来尾部风险的准确预测指标*CBOE的VIX指数(the CBOE volatility index)由S&P500指数期权的隐含波动率估计得到，被市场广泛用于评估未来的波动风险，也被称为“恐慌指数”.由于VIX指数大获成功并有后续金融产品如VIX期货和期权出现，CBOE继续推出由S&P500指数期权的隐含偏度估计得到的SKEW指数，希望评估市场未来可能的尾部风险..

本文的研究在实际中和学术上均具重要意义.在实际市场中，一方面，由于金融危机的影响，尾部风险这一人们最为恐惧、对投资者心态影响最严重、至今人类依然难以把握的黑天鹅事件，多年来一直是市场的关注焦点之一；另一方面，期权市场作为多维交易市场，其信息含量特别丰富：期权交易不仅反映了投资者对未来涨跌方向的预期，还反映了投资者对未来波动大小的预期；期权交易不仅反映了预期的均值，不同到期期限、不同种类和不同行权价的丰富期权交易数据还提供了未来整体概率分布、包括尾部风险的信息.因此近年来，解读和利用期权价格隐含信息的实际应用大量涌现，美国CBOE交易所推出的VIX指数和SKEW指数正是其典型代表.相应地，在学术方面，对偏度等高阶矩的研究、对尾部风险的研究、期权市场隐含信息的解读和运用等都是近年来国外金融学术研究的热点，国内的相关研究刚刚开展，如郑振龙等[15]、郑振龙[16]、刘杨树等[17]、陈蓉和方昆明[18]、陈蓉和吕恺[19]等*从本文参考文献可以看出，近年来此类领域的大量文献发表在国际的Top Journals和国内权威刊物上..本文的研究，首次对期权隐含三阶矩(偏度)是否真的能准确预测未来的尾部风险进行了深入考察，首次提出股指期权中的隐含三阶矩并不是对尾部风险的准确预期，却与投资者情绪显著相关，体现为非理性预期，相信对现有的同领域研究将提供重要的补充.

1　实证设计

1.1波动率偏斜的度量

如前所述，波动率偏斜是指隐含波动率是期权执行价格/在值程度的递减函数，隐含波动率曲线向右下方倾斜.与近年相关文献一致，本文以在值程度作为度量标准，并将期权的在值程度定义为

其中K是期权的执行价格；St是t时刻指数价格；r是无风险利率；T-t为期权的剩余期限.以-5%和5%的在值程度为界，本文将看涨和看跌期权分为3类，分别为虚值(OTM)期权、平值(ATM)期权和实值(ITM)期权*注意，在值程度小于-5%为虚值看跌期权和实值看涨期权，大于5%则为实值看跌期权和虚值看涨期权..

为了更好地挖掘隐含波动率的信息，控制期权剩余期限的影响，本文进一步将期权按剩余期限分类，分为7天至30天、31天至60天和61天至90天(下文分别简称为短、中、长期)*由于一般来说，人们对未来较短时间内的跳跃和尾部风险较具预测力，因此借鉴相关同类文献的做法，本文最长考察期为90天，相应将30天、60天、90天定义为短、中、长期.而与其他同类研究一样，由于到期期限小于7天的期权往往定价误差较大，本文将其剔除.3类.为简化起见，假设在同一分类中，期权到期月是一样的.

在此基础上，本文使用了3种方法来直接刻画波动率偏斜：

1)借鉴文献[8]，以虚值看跌期权的隐含波动率与平值看涨期权的隐含波动率之差为波动率偏斜，即

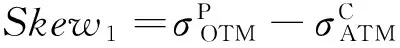
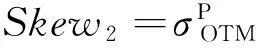
3)Bates[3]指出，股市暴跌会使得OTM看跌期权的隐含波动率高于ITM看涨期权的隐含波动率，因此第3种得到波动率偏斜的方法是将虚值看跌期权的隐含波动率减去实值看涨期权的隐含波动率，即

从以上3种指标的计算过程中可以看出，这些波动率偏斜指标越大，负偏的越明显，反之正偏越明显.

1.2风险中性偏度的度量

在引言中已经谈到，不少学者公认风险中性偏度与波动率偏斜含有类似的信息，Conrad等[9]就是用风险中性偏度代替波动率偏斜，对其与未来收益率的关系进行了研究.因此本文也引入这一指标.

作为期权价格中隐含的资产价格未来分布的偏度，风险中性偏度可以直接通过无模型(model-free)的方法得到[20], 或者通过估计整个风险中性概率分布获得[21,22].其中，无模型方法不需要人为设定模型，所利用的期权市场价格能够有效地捕捉投资者对市场的预期信息[2,1,23]，因而获得很多学者的青睐，在进行相关研究时一般都采用无模型办法来提取风险中性偏度，如Conrad等[9].

与近年来的相关研究一致，本文也采用Bakshi等[20]的无模型方法，从虚值看涨和看跌期权价格中提取风险中性偏度.具体定义如下

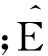
式中K为期权的执行价格；C(t,T;K)表示T时刻到期，执行价格为K的看涨期权价格；P(t,T;K)表示T时刻到期，执行价格为K的看跌期权的价格.可以看出，无模型方法的优点在于，不需要进行模型和参数假设，而是直接运用市场虚值看涨看跌期权的价格积分后提取信息，从而在很大程度上保证了信息的纯粹性和真实性.

由于Skewness直接就是偏度本身，因此该指标与前3种波动率偏斜指标的数值含义刚好相反：指标越大，正偏越明显；指标越小，负偏越明显.

1.3市场尾部风险的度量

借鉴文献[14]，本文使用日百分比收益率的历史分位点*本文也用LM方法(Lee和Mykland[24])度量了尾部风险，发现LM方法下出现跳跃次数较少的情形，不满足进行Logistic回归的数据要求，导致回归效果不佳.因此用日百分比收益率的历史分位点来度量S&P 500指数的尾部风险.在稳健性检验部分，进一步引入Marin和Oliver[25]的方法，以超过两个标准差作为暴涨暴跌的指标.来度量S&P 500指数的尾部风险，正负尾部临界值分别为上涨2.57%和-2.89%，对应样本期内的5%分位数.若某日的指数收盘价变动率超过了这个临界值，则表明该日发生了尾部事件.

以上计算方法是本文定义市场尾部风险的基础，但由于本文考察的是期权价格是否含有未来市场尾部风险的信息，本文并不看重市场尾部事件发生的具体时点，所考察的是一定时间段内是否发生了尾部事件.

举例而言，在t交易日，分别有短、中、长期3类期权在交易，在提取得到相应的短、中、长期波动率偏斜和风险中性偏度之后，本文进一步考察从t日开始的30天、60天和90天观测窗口期内，市场发生尾部事件的情形，以研究波动率偏斜和风险中性偏度是否对这些真实尾部事件具有预测力.

但与现有文献不同的是，为了深入检验风险中性高阶矩对尾部风险的预测力，本文除了仅对“是否发生尾部事件”进行研究，还进一步对尾部事件进行了细分：在观测窗口期内，若仅发生暴跌，则定义t日的尾部风险指标TailRiskt=1；若仅发生暴涨，则TailRiskt=2；若先暴跌后暴涨，则TailRiskt=3；若先暴涨后暴跌，则TailRiskt=4；否则TailRiskt=5，即在观测窗口期内无暴涨暴跌.

1.4尾部风险预测模型设定

在仅仅研究波动率偏斜指标与风险中性偏度指标是否对发生暴跌具有预测性时，本文采用的是简单的Logistic模型

=αj+βjSkewIndext+εt

(1)

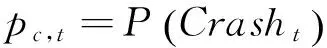
在对尾部风险进行细分研究时，由于本文所定义的市场尾部风险为定性变量，且5个不同的取值(1，2，3，4，5)并无次序和等级关系，因此采用多项Logistic模型来分析，具体模型为

=αj+βjSkewindext+εt

(2)式中pj,t=P(TailRiskt=j)，即t时刻起观测窗口期内发生第j种尾部风险的概率(j= 1, 2, 3, 4, 5).本文对短、中、长期期权均进行Logistic回归.

1.5投资者情绪

如引言所述，与同类研究不同，本文在考察完尾部风险预测效果之后，还额外考虑了非理性预期的可能性，进一步研究波动率偏斜/风险中性偏度与投资者情绪之间的关系，以考察其究竟是尾部风险的真实预期，还是体现了非理性预期的影响.

借鉴Baker和Wurgler[26]，利用主成分分析法，基于6个可能的投资者情绪变量构建出投资者情绪的综合指标，称之为投资者情绪指数.然后将波动率偏斜/风险中性偏度指标对投资者情绪进行单变量回归，考察其相关性.

这6个投资者情绪变量包括封闭式基金的折价、股票的换手率、IPO个数、IPO首日收益率、新发行的股权及红利溢酬.情绪指数越大，反映投资者对未来越乐观；反之越悲观.这部分的实证数据来自Wurgler的教学主页，时间跨越2000-11～2010-12，共计122个月度数据.相应地，在进行回归时，本部分所用到的波动率偏斜与风险中性偏度指标均采用月内平均方式转换为月度数据，月度数据的风险中性偏度与波动偏斜并不存在自相关，故在进行线性回归时无需进行自相关调整.

2　样本与数据

本文选用2000-11-03～2011-04-29的S&P 500指数期权，涵盖非危机、次贷危机和危机后时期，样本较具一般性，共2 636个交易日，2 440 348只期权数据，数据来自CBOE.文章中使用的无风险利率为美联储网站的美国国库券利率*数据分析中需用到非整数期限的利率时，本文用3次样条插值得到对应期限的利率.，VIX指数收盘数据来自CBOE，S&P500指数数据来自雅虎财经.

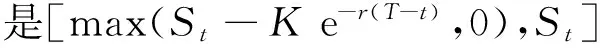
按上述规则筛选后，期权样本的剩余期限与在值程度分布情况见表1.可以看出：从期权品种来看，看跌期权交易量较大；从剩余期限来看，短、中、长期的期权交易数量占比分别为29.9%、41.3%和28.8%，中期期权相对交易量较大；从在值程度来看，40.6%的数据分布在[-10%,-5%)的区域内，[-5%,5%]和(5%,10%]两者的占比分别为31.7%和27.7%.

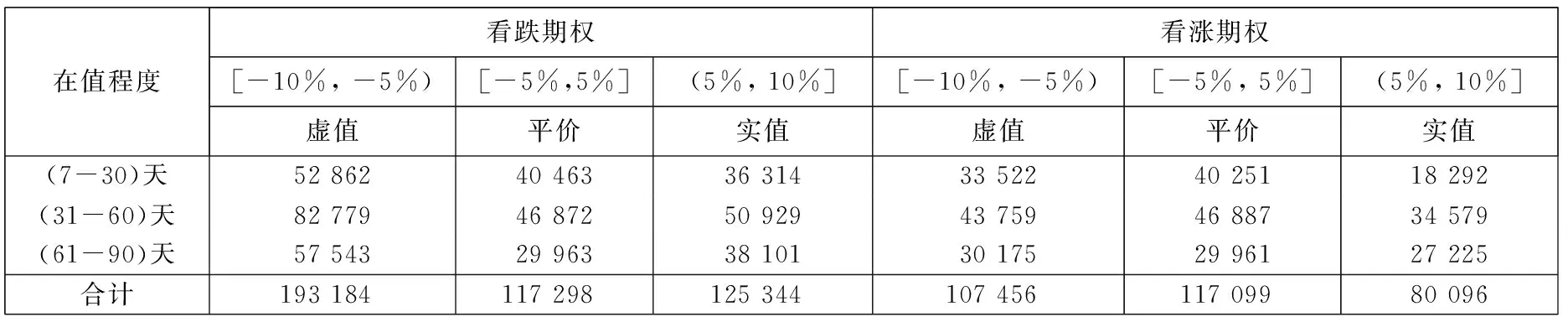
表1　期权样本的期限与在值程度分布

3　实证结果

3.1对暴跌风险的预测效果

首先运用回归式(1)考察了波动率偏斜指标和风险中性偏度指标是否能够预测未来的暴跌风险，结果如表2所示.

从模型设定和方程解释能力来看，尽管较小的伪R2意味着解释能力有限，但似然比卡方指标(LR)显著拒绝了“模型无效”的原假设，说明期权价格中提取的波动率偏斜和风险中性偏度的确含有未来对应时段内暴跌风险的信息.

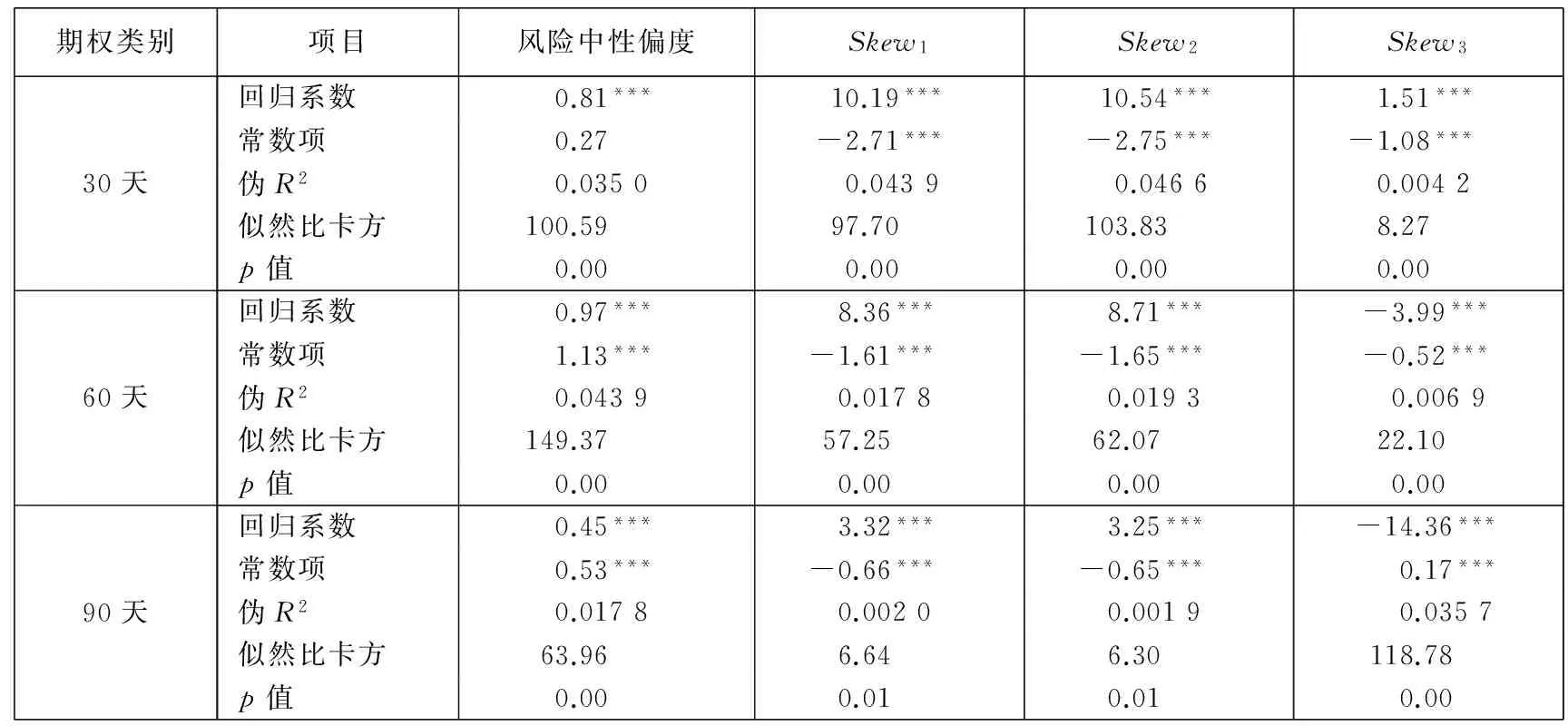
表2　波动率偏斜、风险中性偏度与市场暴跌风险*　　为节省篇幅起见，本文的实证结果均直接报告显著性水平.

注:“***”、“**”和“*”分别表示经Newey-West调整的1%、5%和10%的显著性水平.

从回归系数来看，除了第3个波动率偏斜指标结果较不稳定之外，风险中性偏度和前两个波动率偏斜指标的回归系数均显著为正，这初步表明这些波动率偏斜指标和风险中性偏度指标对未来的暴跌风险均具有显著的预测力.但细看之下，由于风险中性偏度与波动率偏斜的指标含义是相反的，回归系数都为正，其经济含义实际上是相悖的.表2的回归结果表明：风险中性偏度越小，即负偏程度较小时，未来发生暴跌的机率反而显著下降；而前两种波动率偏斜指标越大，即负偏程度越大，未来发生暴跌的机率越大.这一结果实际上和现有的主要研究发现是一致的：Conrad等[9]采用风险中性偏度进行研究时，发现越负偏，个股未来收益越高；而Xing等[8]采用波动率偏斜指标进行研究时，却发现越负偏，个股未来收益越低.本文的研究结果在一定程度上表明，至少在日数据上，风险中性偏度与波动率偏斜可能并不完全含有相同的信息*关于波动率偏斜与风险中性偏度为何结论不一致，目前尚未有研究解决这一问题.从指标构造来说，波动率偏斜是两个不同行权价的Black-Scholes隐含波动率之差；而风险中性偏度并不依赖于特定的定价模型，而是直接运用市场期权价格得到“无模型”的估计结果，并且是系列虚值看涨期权和虚值看跌期权积分的结果.这可能是两者的差异原因.此外，Zhang和Xiang[27]发现隐含波动率斜率是风险中性偏度的1/6，隐含波动率曲度是风险中性峰度的1/24.但这些都无法完全解释各文献中发现的两者信息刚好相反的现象.由于本文的主题在于研究这两个指标能否预测尾部风险，关于这两个指标的差异原因，需从指标构建的角度来深入研究，笔者将专文研究，就不在此赘述..

无论如何，如果仅看表2的结果，很容易得出一个结论，波动率偏斜和风险中性偏度对未来的暴跌(左尾)风险的确具有显著的预测力，这两个指标可以作为未来暴跌风险的预测指标.但是否真的如此呢？我们对尾部风险进行了进一步细分，来详细考察波动率偏斜和风险中性偏度指标的预测准确性.

3.2对细分尾部风险的预测效果

3.2.1风险中性偏度

首先运用式(2)对风险中性偏度的细分尾部风险预测力进行了分析，结果报告在表3中.

可以看出：首先，无论短中长期期权，风险中性偏度的回归系数均在1%的水平上显著异于零，似然比卡方指标(LR)也显著拒绝了“模型无效”的原假设，说明期权价格中提取的风险中性偏度的确含有未来对应时段内尾部风险的信息；当然，Logistic回归的伪R2的值小于5%，说明未来市场尾部风险能被风险中性偏度解释的部分仍然是比较小的.

然而，无论短中长期期权，风险中性偏度的系数均显著为正，也就是说，随着风险中性偏度负偏程度的加剧，相较于既无暴涨也无暴跌的市场状态而言，仅发生暴跌、仅发生暴涨、先暴跌后暴涨、先暴涨后暴跌4种状态的概率都显著下降.这意味着，事前投资者无法根据期权价格中的隐含风险中性偏度的大小或变化，对未来的尾部风险作出准确的判断.从期限来看，风险中性偏度对市场尾部风险的解释力度也并未如预期随着预测期限的增长而减弱.

总之，表3的结果表明，风险中性偏度的确含有未来市场尾部风险的信息，但投资者却无法基于此作出合理准确的预测，事前的风险中性偏度无法准确预测未来的尾部风险.

3.2.2波动率偏斜

接下来，运用式(2)对波动率偏斜的细分尾部风险预测力也进行了回归，结果报告在表4中.

可以看出，对于前两种常见的波动率偏斜指标而言，无论短中长期期权，回归系数绝大部分都是显著异于零的，似然比卡方指标(LR)也显著拒绝了“模型无效”的原假设，说明期权价格中提取的波动率偏斜同样也含有未来对应时段内尾部风险的信息.当然，较低的伪R2值再次说明波动率偏斜对未来市场尾部风险的解释能力有限.

然而，前两种波动率偏斜指标的回归结果比风险中性偏度指标的回归结果更难以得到一致的结论：在大多数情况下，随着波动率偏斜的程度的加剧，相较于既无暴涨也无暴跌的市场状态情形，未来30天、60天和90天内仅发生暴跌、仅发生暴涨、先暴跌后暴涨、先暴涨后暴跌4种状态的概率都显著上升；但波动率偏斜加剧后，未来60天内暴跌的概率却反而显著下降了(两种波动率偏斜指标的回归系数分别为-5.46和-5.32，均在1%的水平下显著异于零)；第二种波动率偏斜指标的加剧对未来90天内的市场先暴涨后暴跌并无预测力(回归系数为3.40，不显著).从期限来看，波动率偏斜对市场尾部风险的解释力度也并未随着预测期限的增长而减弱.再观察Skew3的回归系数，或者不显著，或者显著为负，也就是说，OTM看跌期权的隐含波动率越高于ITM看涨期权的隐含波动率，也不能得出市场越易发生暴跌.

3.2.2细分尾部风险的一般结论

将本文结果与现有研究相比较，认为，之前的研究之所以得出波动率偏斜程度与未来市场的暴跌正相关，很大原因在于从来没有人对未来市场的尾部风险进行细分，而是如同本文3.1那样将暴跌、先暴涨后暴跌、先暴跌后暴涨等只要有发生过暴跌的情形均归为一类，因此认为波动率偏斜对未来的市场暴跌具有预测性.实际上，当对尾部风险进行细分之后，得到了与现有研究不同的结论：波动率偏斜/风险中性偏度的确在一定程度上反映了投资者对未来尾部风险的预期，但却并非准确的预期.因此，接下来引入投资者情绪，考察这一预期中是否存在非理性的影响.

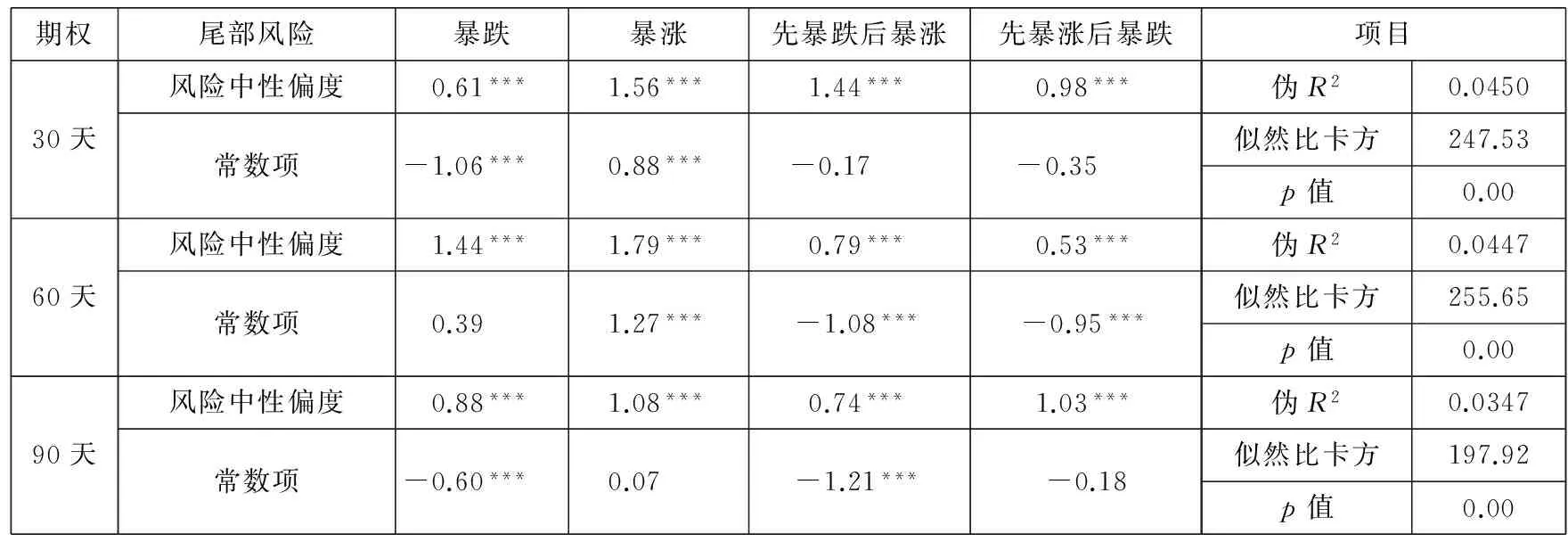
表3　风险中性偏度与细分尾部风险

注:“***”、“**”和“*”分别表示经Newey-West调整的1%、5%和10%的显著性水平.

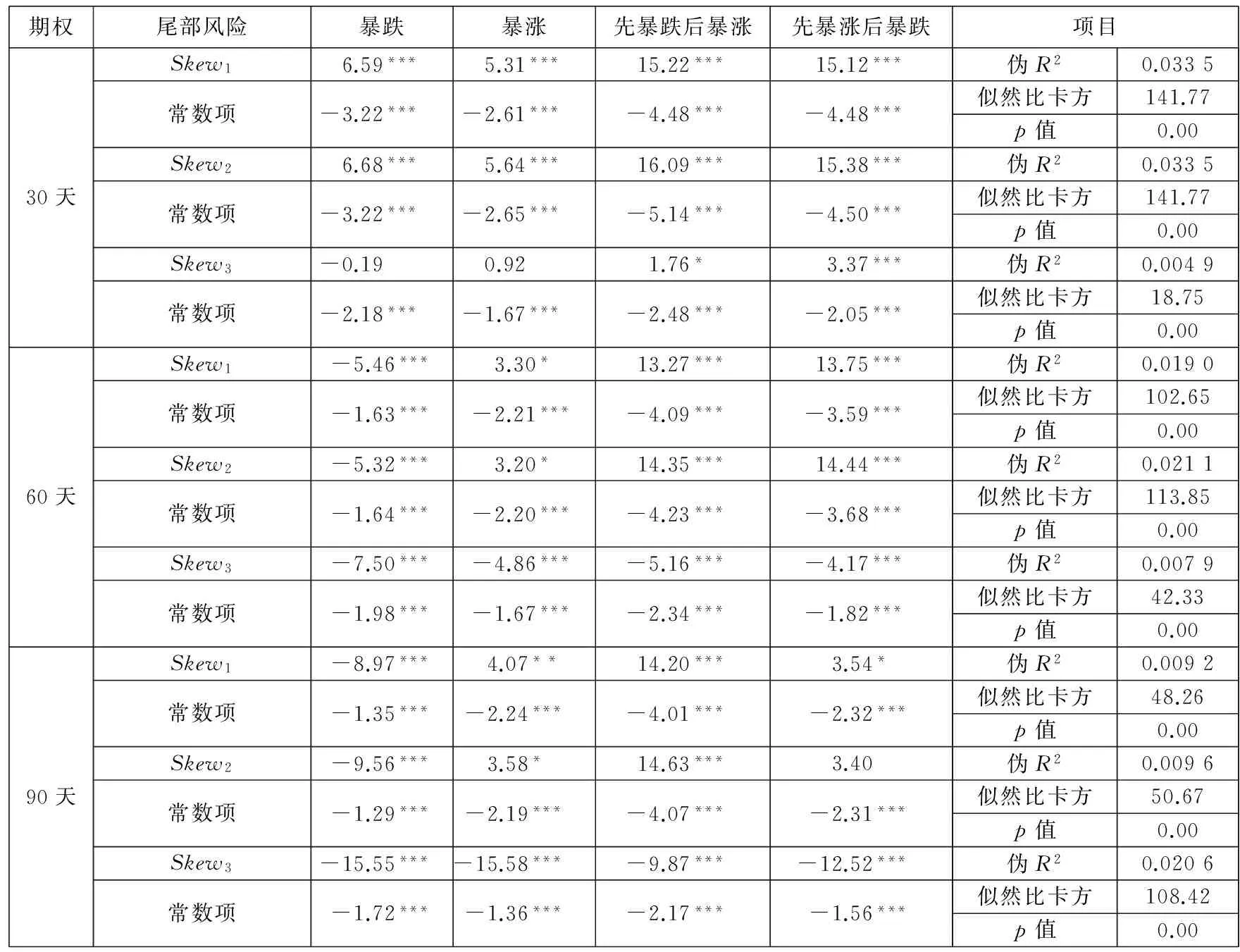
表4　波动率偏斜与市场尾部风险

注:表中Skew1、Skew2和Skew3分别表示虚值看跌与平价看涨隐含波动率之差、虚值看跌与平价看涨看跌隐含波动率之差、虚值

3.3与投资者情绪的相关性

3.3.1风险中性偏度与投资者情绪

表5给出了月度风险中性偏度与投资者情绪的单变量回归结果.可以看出在月度平均之后，短、中、长期的风险中性偏度都与情绪指数存在显著为正的相关性.也就是说，投资者越看空未来市场，投资者情绪指标越下降，风险中性偏度越小，即越负偏；反之，投资者情绪越乐观，风险中性偏度越大，即越正偏.这一结果与直觉是一致的.因此，本部分的研究结果表明，风险中性偏度与投资者情绪显著相关.

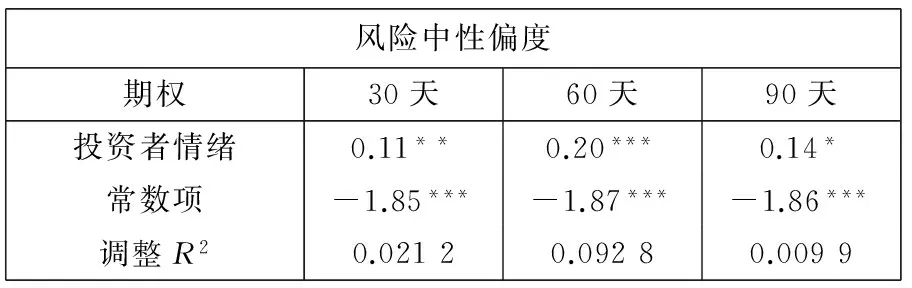
表5　风险中性偏度与投资者情绪

注:“***”、“**”和“*”分别表示1%、5%和10%的显著性水平.

表6给出了月度波动率偏斜与投资者情绪的回归结果.可以看出，除了短期的前两个波动率偏斜指标与市场投资者情绪无显著关系，其他情形下月度波动率偏斜与情绪指数的回归系数均显著为负.也就是说，投资者越悲观，市场情绪指数越低，波动率偏斜程度总体越大；反之，投资者越乐观，市场情绪指数越高，波动率偏斜程度总体越小.而且呈现出期限越长，与投资者情绪的相关性越显著的现象.这也与我们的经济直觉一致：波动率偏斜同样也与投资者情绪显著相关；预测期越长，受投资者情绪影响越大.

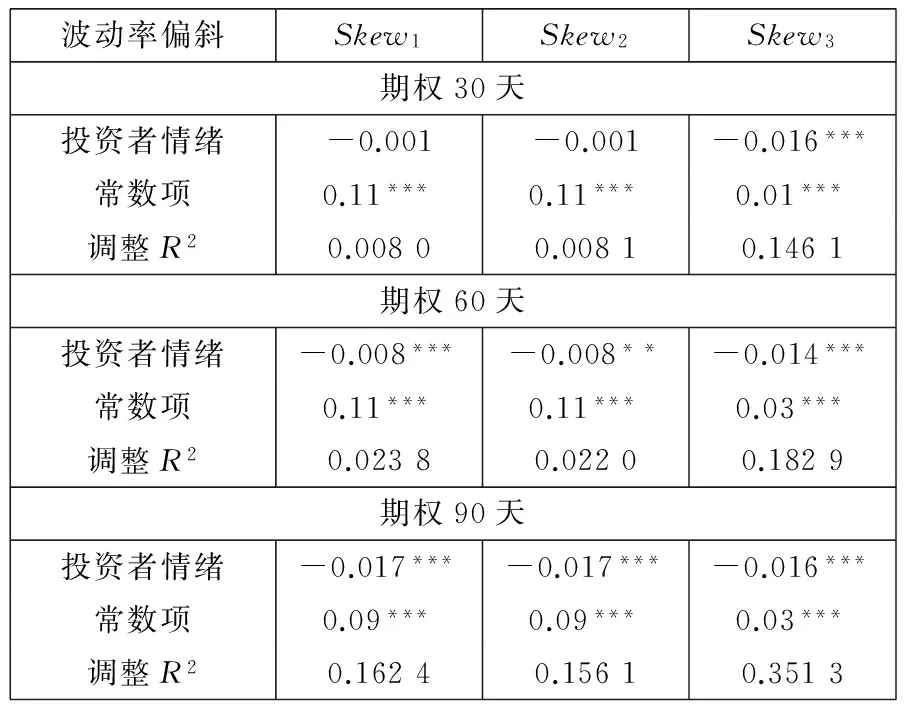
表6　波动率偏斜与投资者情绪

注:“***”、“**”和“*”分别表示1%、5%和10%的显著性水平.

3.3.3投资者情绪的一般结论

从上述研究可以看出，风险中性偏度和波动率偏斜指标在预测未来尾部风险时，并不能获得一致稳定的结论，但它们与投资者情绪的相关性却是相当稳定、显著和合理的.Han[28]对S&P500期权市场的研究也表明，期权隐含波动率的斜率和风险中性偏度与各种投资者情绪指标呈显著的合理关系.这表明，至少对于美国S&P500股指来说，未来的市场尾部风险并不能在目前的股指期权市场中得到准确的预测*由于涉及到公司运营和财务信息，个股的信息有可能提前体现在个股期权市场中.但本文对S&P500股指的研究则表明，这个市场是相当有效率的，即使是期权市场，也并未包含对股指未来预测有用的信息.，风险中性偏度和波动率偏斜指标受到投资者情绪的显著影响，更多地体现为非理性预期.

4　稳健性检验

4.1细分宏观经济背景

为检验前文研究结果的稳健性，首先对宏观经济背景进一步细分，分别对次贷危机前、中、后的数据进行式(2)回归，考察不同经济背景下波动率偏斜/风险中性偏度对尾部风险的预测力.一般公认，2007年2月13日汇丰控股为其在美次级房贷业务增加18亿美元坏账拨备是次贷危机拉开序幕的标志性事件；2009年3月11日花旗银行的财务数据表明该公司恢复危机前的盈利，道指暴涨5.8%，创2009年最大涨幅，则被认为标志着次贷危机最危险的时期已过.本文就以这两个日期为节点，将样本期中的2000-11-03～2007-02-12、2007-02-13～2009-03-10和2009-03-11～2011-04-29划分为危机前、中、后进行研究.结果如表7和表8所示.

可以看出，前文的基本结论仍然是成立的.虽然大部分回归的似然比卡方指标(LR)均显著拒绝了“模型无效”的原假设，但较低的伪R2值依然表明，市场尾部风险能被风险中性偏度/波动率偏斜解释的部分很小.

更重要的是，在划分不同经济背景之后，风险中性偏度的回归系数除了少数不显著和一个显著为负(危机前90天对暴跌的回归系数为-0.14)，其余均显著为正，这与表3的回归基本相同，说明投资者无法依据风险中性偏度对未来的确切尾部风险作出准确的判断.

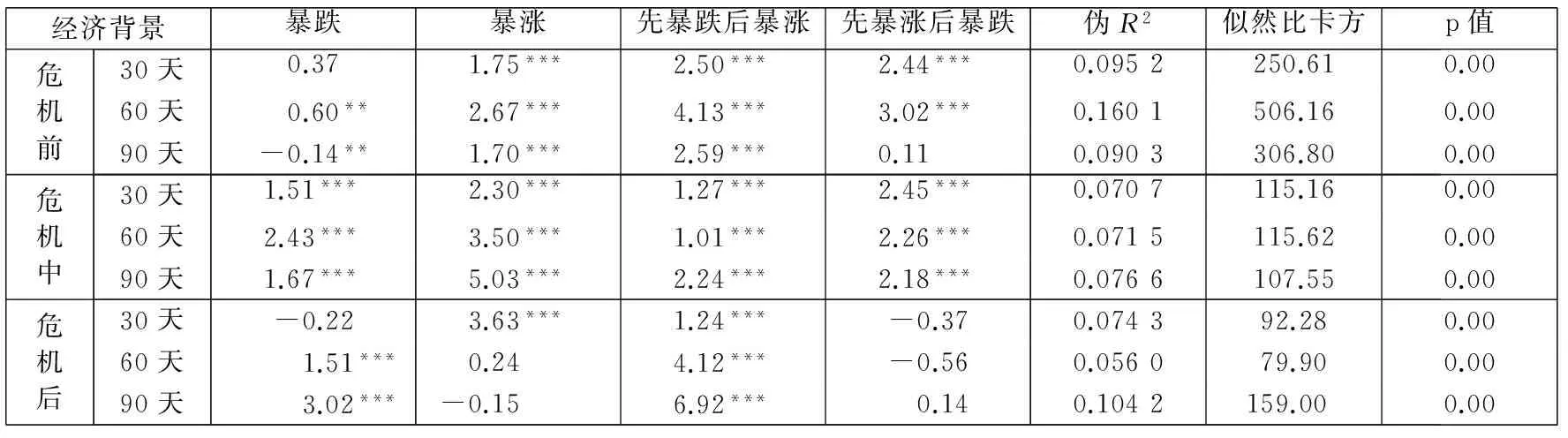
表7　风险中性偏度与不同经济背景下的细分尾部风险

注:为简洁起见，本表将常数项的回归结果略去，仅报告了不同经济背景下，不同期限期权隐含的风险中性偏度的回归系数及

其显著性；‘“***”、“**”和“*”分别表示经Newey-West调整的1%、5%和10%的显著性水平.

而在划分不同经济背景之后，波动率偏斜的回归结果比表4更难以得到一致的结论：理论上暴跌的回归系数应该显著为正，暴涨的回归系数应该显著为负，意味着越负偏，暴跌概率越大，暴涨概率越小.但在表8中，不显著的、显著为正的、显著为负的回归系数都存在.这与前文的研究结论”波动率偏斜/风险中性偏度对未来市场尾部风险的预测并不准确”是一致的.

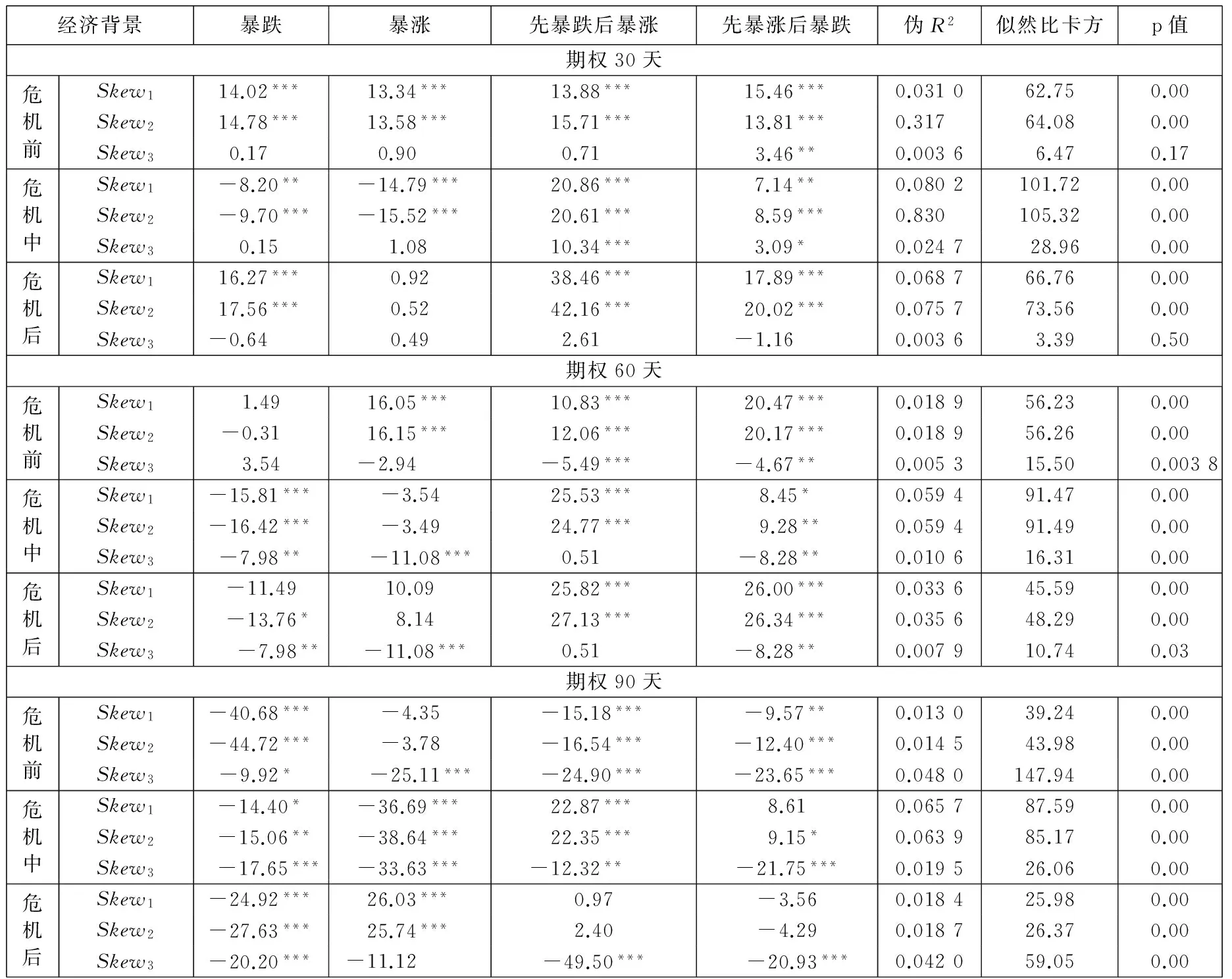
表8　波动率偏斜与不同经济背景下的细分尾部风险

注: 表中Skew1、Skew2和Skew3分别表示虚值看跌与平价看涨隐含波动率之差、虚值看跌与平价看涨看跌隐含波动率之差、虚值

看跌与实值看涨隐含波动率之差；为简洁起见，本表将常数项的回归结果略去，仅报告了不同经济背景下，不同期限期权隐

含的波动率偏斜的回归系数及其显著性；“***”、“**”和“*”分别表示经Newey-West调整的1%、5%和10%的显著性水平.

4.2改变尾部风险与在值程度的度量方式

主要考虑两种情形：一是改变尾部风险的度量方式，采用Marin和Oliver[25]等的定义，若某天的收益率与其均值之差大于两个标准差则为暴涨，若该天的收益率与其均值之差小于两个标准差则为暴跌；二是改变在值程度的衡量，这是稳健性检验中常用的做法，借鉴Bollen和Whaley[5]按Delta值分类的方法，具体分类见表9.

表9　期权按Delta分

稳健性检验的回归结果如表10和表11所示.可以看出，随着风险中性负偏的加剧和前两种波动率偏斜指标的加大，相较于既无暴涨也无暴跌的市场状态而言，仅发生暴跌、仅发生暴涨、先暴跌后暴涨、先暴涨后暴跌4种状态的概率都显著上升，第3种波动率偏斜指标的回归结果则部分不显著，部分显著为负.这与前一部分的结论仍然相似，风险中性偏度/波动率偏斜包含市场尾部风险的信息，但是却并不能准确预测未来市场尾部风险发生的状态.

接下来，将新度量的波动率偏斜对投资者情绪进行回归*在值程度的度量变化并不会影响风险中性偏度，因此无需对风险中性偏度进行稳健性检验.，以验证波动率偏斜与投资者情绪的关系.从表12可以看出，波动率偏斜对投资者情绪的回归系数大多显著为负，与前文的结论仍然基本一致，表明即使更换计算方式，波动率偏斜依然与投资者情绪显著相关.

表10　风险中性偏度与市场尾部风

注:“***”、“**”和“*”分别表示经Newey-West调整的1%、5%和10%的显著性水平.

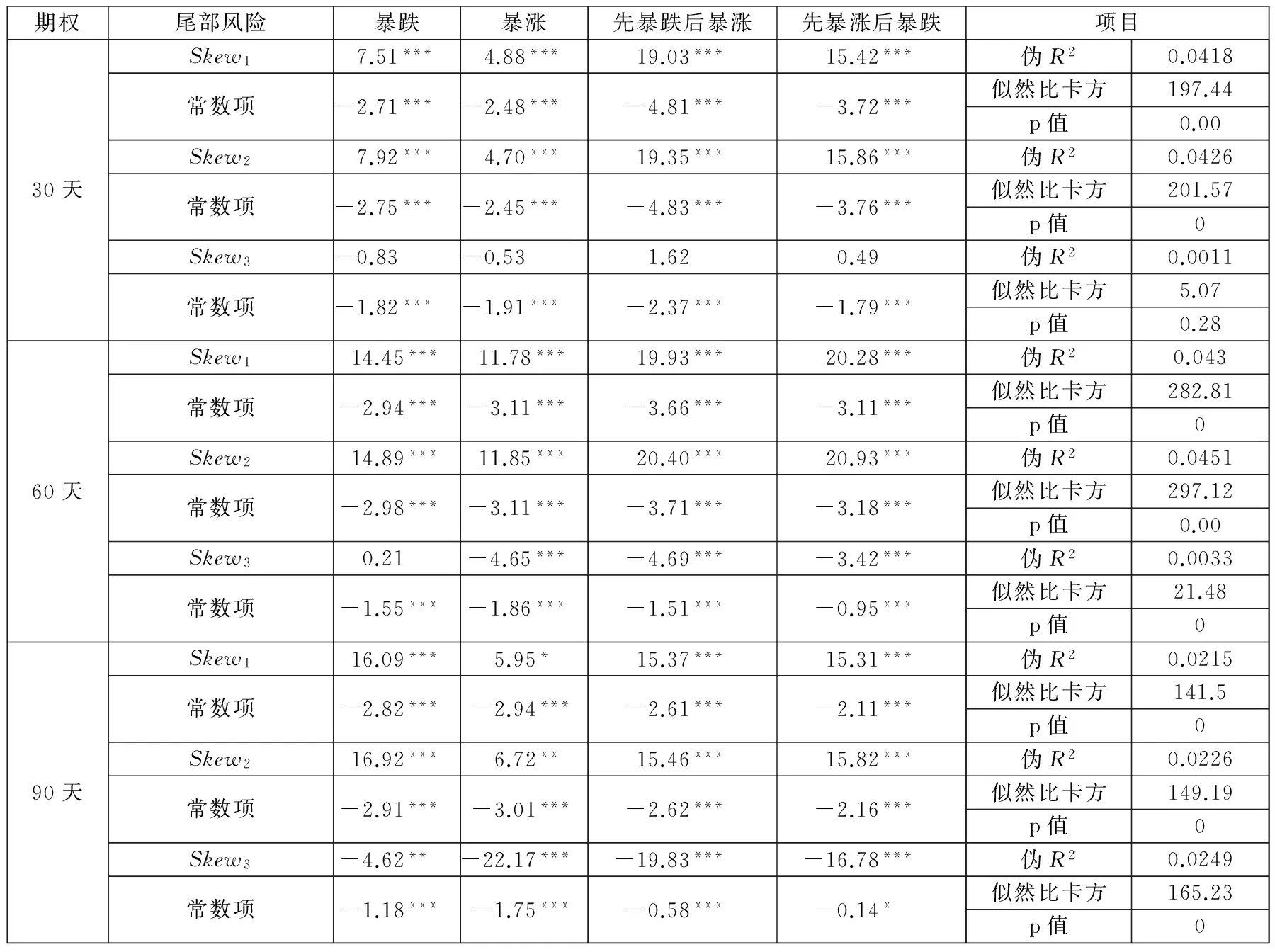
表11　波动率偏斜与市场尾部风险

注:表中Skew1、Skew2和Skew3分别表示虚值看跌与平价看涨隐含波动率之差、虚值看跌与平价看涨看跌隐含波动率之差、虚值

看跌与实值看涨隐含波动率之差；“***”、“**”和“*”分别表示经Newey-West调整的1%、5%和10%的显著性水平.

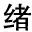
表12　波动率偏斜与投资者情

注:“***”、“**”和“*”分别表示1%、5%和10%的显著性水平.

5　结束语

期权市场隐含的波动率偏斜与风险中性偏度是否对未来真实尾部风险的良好预测？本文采用Logistic模型对其预测力进行了直接研究.结果发现，在S&P500股指期权市场上，如果仅就暴跌风险而言，波动率偏斜/风险中性偏度似乎具有显著的预测力；但一旦对尾部风险加以细分，就可以发现，波动率偏斜/风险中性偏度的确含有未来市场尾部风险的信息，但却并不能准确预测未来市场尾部风险发生的状态.从期限来看，波动率偏斜/风险中性偏度对市场尾部风险的解释力度也没有随着预测期限的增长而减弱.因此，用波动率偏斜/风险中性偏度直接作为尾部风险的预测指标，至少在S&P500股指期权市场上，是危险的.

反之，对波动率偏斜/风险中性偏度与市场情绪的关系研究却表明，基于6个变量构建出的投资者情绪综合指数与S&500指数期权的波动率偏斜与风险中性偏度存在显著相关关系.这意味着，至少在本文的样本期内，股指期权市场中形成的未来尾部风险预期，更多地是受投资者情绪影响的非理性预期.

本文是第一篇对比考察期权隐含波动率偏斜究竟反映的是准确预期还是投资者情绪的文章，首次全面细致地考察了波动率偏斜风险中性偏度与上下尾部风险的关系，并得到了与前人不同的重要结论.从后续研究来说，可以对横截面个股也进行类似的研究；波动率偏斜与风险中性偏度的异同值得深入考察；此外，期权市场中隐含的理性预期与非理性预期成分及其对市场的影响，值得进一步深入研究.

[1]Rubinstein M. Implied binomial trees[J]. Journal of Finance, 1994, 49(3): 771-818.

[2]Bates D S. The crash of '87: Was it expected? The evidence from options markets[J]. Journal of Finance, 1991, 46(3): 1009-1044.

[3]Bates D S. Post-'87 crash fears in the S&P 500 futures option market[J]. Journal of Econometrics, 2000, 94(1/2): 181-238.

[4]Pan J. The jump-risk premia implicit in options: Evidence from an integrated time-series study[J]. Journal of Financial Economics, 2002, 63(1): 3-50.

[5]Bollen N B P, Whaley R E. Does net buying pressure affect the shape of implied volatility functions?[J]. The Journal of Finance, 2004, 59(2): 711-753.

[6]Evans R B, Geczy C C, Musto D K, et al. Failure is an option: Impediments to short selling and options prices[J]. Review of Financial Studies, 2009, 22(5): 1955-1980.

[7]Garleanu N, Pedersen L H, Poteshman A M. Demand-based option pricing[J]. Review of Financial Studies, 2009, 22(10): 4259-4299.

[8]Xing Y, Zhang X, Zhao R. What does the individual option volatility smirk tell us about future equity returns?[J]. Journal of Financial and Quantitative Analysis, 2010, 45(3): 641-662.

[9]Conrad J, Dittmar R F, Ghysels E. Ex ante skewness and expected stock returns[J]. The Journal of Finance, 2013, 68(1): 85-124.

[10]Bali T G, Hovakimian A. Volatility spreads and expected stock returns[J]. Management Science, 2009, 55(11): 1797-1812.

[11]Yan S. Jump risk, stock returns, and slope of implied volatility smile[J]. Journal of Financial Economics, 2011, 99(1): 216-233.

[12]Doran J S, Peterson D R, Tarrant B C. Is there information in the volatility skew?[J]. The Journal of Futures Markets, 2007, 27(10): 921-959.

[13]Bahra B. Implied Risk-Neutral Probability Density Functions from Option Prices: Theory and Application[R]. Bank of England UK, 1997.

[14]Dennis P, Mayhew S. Risk-neutral skewness: Evidence from stock options[J]. Journal of Financial and Quantitative Analysis, 2002, 37(3): 471-493.

[15]郑振龙, 王磊, 王路跖. 特质偏度是否被定价?[J]. 管理科学学报, 2013, 16(5): 1-12.

Zheng Zhenglong, Wang Lei, Wang Luzhi. Is the risk of idiosyncratic skewness priced?[J]. Journal of Management Sciences in China, 2013, 16(5): 1-12. (in Chinese)

[16]郑振龙. 资产价格隐含信息分析框架: 目标、方法与应用[J]. 经济学动态, 2012, (3): 33-40.

Zheng Zhenglong. The implied information of financial assets prices: Goals, approaches and applications[J]. Economic Perspectives, 2012, (3): 33-40. (in Chinese)

[17]刘杨树， 郑振龙， 张晓南. 风险中性高阶矩: 特征、风险与应用[J]. 系统工程理论与实践, 2012, 32(3): 647-655.

Liu Yangshu, Zheng Zhenglong, Zhang Xiaonan. Risk-neutral higher moments: Characteristics, risks and applications[J]. Systems Engineering-Theory & Practice, 2012, 32(3): 647-655. (in Chinese)

[18]陈蓉, 方昆明.波动率风险溢酬: 时变特征及影响因素[J].系统工程理论与实践, 2011, 31(4): 761-770.

Cheng Rong, Fang Kunming. Volatility risk premium in Hong Kong stock market[J]. Systems Engineering-Theory & Practice, 2011, 31(4): 761-770. (in Chinese)

[19]陈蓉, 吕恺. 隐含波动率曲面: 建模与实证[J]. 金融研究, 2010, (8): 136-154.

Cheng Rong, Lü Kai. Implied volatility surface: Modeling and empirical test[J]. Journal of Financial Research, 2010, (8): 136-154. (in Chinese)

[20]Bakshi G, Kapadia N, Madan D. Stock return characteristics, skew laws, and the differential pricing of individual equity options[J]. Review of Financial Studies, 2003, 16(1): 101-143.

[21]Breeden D T, Litzenberger R H. Prices of state-contingent claims implicit in options prices[J]. Journal of Business, 1978, 51(4): 621-651.

[22]Aït-Sahalia Y, Lo A W. Nonparametric estimation of state-price densities implicit in finance asset prices[J]. Journal of Finance, 1998, 53(2): 499-547.

[23]Jackwerth J, Rubinstein M. Recovering probability distributions from option prices[J]. Journal of Finance, 1996, 51(5): 1611-1631.

[24]Lee S S, Mykland P A. Jumps in financial markets: A new non-parametric test and jump dynamics[J]. Review of Financial Studies, 2008, 21 (6): 2535-2563.

[25]Marin J M, Olivier J P. The dog that did not bark: Insider trading and crashes[J]. The Journal of Finance, 2008, 63(5): 2429-2476.

[26]Baker M, Wurgler J. Investor sentiment and the cross-section of stock returns[J]. The Journal of Finance, 2006, 61(4): 1645-1680.

[27]Zhang J E, Xing Y. The implied volatility smirk[J]. Quantitative Finance, 2008, 8(3): 263-284.

[28]Han B. Investor sentiment and option prices[J]. The Review of Financial Studies, 2008, 21(1): 387-414.

Can implied volatility skew or risk-neutral skewness predict tail risk?

CHEN Rong, LIN Xiu-que

Department of Finance, Xiamen University, Xiamen 361005, China

The paper extracts the implied volatility skew and the risk-neutral skewness from the S&P500 index option data and uses the logistic model to explore whether the volatility skew and the risk-neutral skewness are good estimators of future tail risk. The results show that both contain some information about future tail risk but cannot predict it accurately. Instead, the volatility skew and the risk-neutral skewness are both significantly correlated with investor sentiments.

implied volatility skew; risk-neutral skewness; tail risk; investor sentiments

2013-09-12；

2014-03-21.

国家自然科学基金资助项目( 71471155； 71371161)； 国家自然科学青年基金资助项目(71101121).

陈蓉(1976—)， 女， 福建福清人， 博士， 教授. Email: aronge@xmu.edu.cn

F832.51

A

1007-9807(2016)03-0113-14