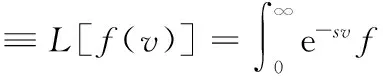代理成本与“信用价差之谜”
牛华伟
(1. 南京审计大学金融学院, 南京 211815;2. 南京审计大学江苏省金融工程重点实验室, 南京 211800)
代理成本与“信用价差之谜”
牛华伟1, 2
(1. 南京审计大学金融学院, 南京 211815;2. 南京审计大学江苏省金融工程重点实验室, 南京 211800)
作为一个内生因素,企业中的代理问题可能会恶化企业的信用风险.通过将代理人与股东之间的最优合约模型嵌入到Leland-Toft内生违约框架中,研究了道德风险这一具体的代理问题对信用风险及信用价差的影响机制.结论表明:企业中的道德风险问题对企业信用风险产生明显影响,并且显著增加信用价差;对于描述道德风险的关键参数,论文建立的模型明确了它们在影响信用价差中起到的作用.由此,论文从代理问题的角度对“信用价差之谜”给出了合理解释.此外,文中也给出了债券价值、股权价值和内生违约边界的显性表达式.
信用价差; 委托代理; 道德风险; 信用风险; Poisson风险
0 引 言
企业债券的收益率相对于无风险利率的价差直接决定了企业的融资成本,通常这个价差被称为企业债券的信用价差(credit spread).由于信用风险导致信用价差,因此在公司金融和资产定价中,主要的研究兴趣之一便是如何计算信用风险导致的违约概率.然而,如众所周知,利用结构化模型(structural models)计算违约概率会低估企业债券的信用价差,特别是债务期限较短的投资级债券.文献[1]发现,对于不同的结构化模型,如果用历史违约率和回收率数据校准模型参数,这些模型都会产生类似的信用价差,而这些信用价差均远低于实际价差的历史平均水平.实际价差与模型得到的理论价差之间存在“宽缺口”(wide gap)的现象通常被称为“信用价差之谜”[2].
通过已有的研究认识到,信用价差不仅反映了由企业信用风险导致的违约溢价,同时也反映了其它因素,如税收、宏观经济条件、流动性溢价等*众多研究已经尝试分析了影响信用价差的不同因素, 例如, Duffie和Singleton[3],Feldhutter和Lando[4],Ericsson和Renault[5]与 Longstaff等[6]..因此,近年来众多学者已从宏观经济条件、债券市场的流动性、股权溢价等这些外生的因素解释“信用价差之谜”[7-9].然而这些研究结果表明,即使考虑上述所有的外生因素,理论得到的信用价差仍显著低于实际价差.Chen等[10]指出,解释“信用价差之谜”的关键在于认识到企业违约是逆周期的.而已有的理论研究表明,代理问题也是逆周期的[11].这样,除了上述诸多外生因素外,股东与代理人之间的委托代理问题可能会内生地恶化企业信用风险,进而影响信用价差*Collin-Dufresne等[12]及王安兴等[13]分别对国外和国内公司债价差及价差变化的决定因素进行了研究, 结果发现理论上对信用价差有潜在解释力的外生因素实际上对价差及价差变动的解释能力非常有限, 即使加入所有其他已知的潜在外生变量后, 也只能解释价差变动的35%左右..但目前学术界与业界将违约溢价与代理问题独立对待,从而忽略了代理问题这个内生因素对信用风险及信用价差的影响.
本文建立了一个理论模型,分析企业中的代理问题对其信用风险的影响.具体的,本文考虑的代理问题是动态道德风险问题,它是由于代理人对风险管理所付出的努力程度无法被观察到而引起的,且道德风险问题会影响低频率的大规模损失(或称为Poisson风险)的发生概率*例如,对于工业和金融业企业而言,他们承受的大规模损失,对于前者是生产事故,对于后者是所管理资产的价值出现暴跌.而这些损失的发生与代理人不充分的风险防范相关,这意味着大规模损失的发生概率受到风险防范水平的影响,进而受到代理人对风险管理付出的努力程度的影响..代理人在工作中卸责将提高大规模损失发生的概率,而损失相应的成本都将由股东承担以避免企业破产.股东与代理人之间的这种内在矛盾表明,股东可能会选择过早违约,而这种做法导致企业的信用风险恶化.将代理人与股东之间的连续时间最优合约模型嵌入到结构化框架中[14-16].这个框架采用了Black和Cox[17]的内生违约思想,因此,对于本文讨论的问题这个研究框架是理想的.为了促使代理人努力工作,在当期没有损失发生的前提下,股东将向代理人支付额外奖金作为激励;同时,如果大规模损失发生,股东将承担产生的相应成本.上述两种成本统称为代理成本.
为了分析道德风险对企业信用风险的影响,首先研究在动态道德风险下代理人与股东之间的最优合约.基于Biais等[18]发展的连续时间委托代理模型,本文推导出最优合约的具体形式.考虑上述的代理成本,发展了Leland和Toft[15]的模型,得到股权价值.这样,股权价值由企业的基础价值(即企业无负债资产价值)和期望代理成本决定.当股权价值跌为零时,企业将内生地违约,债权人通过清算企业资产收回部分投资.同时,通过股权价值可得到企业的内生违约边界,计算出企业债券的市场价值或债券的收益率,进而得到债券的信用价差.本文得到的关键结论是,由于存在代理成本道德风险问题使得企业在拥有较高的基础价值时违约.因此,债券的信用价差相对于不考虑代理问题时将显著增加.此外,建立的模型能够量化分析道德风险问题对信用价差的内生影响.
近年来,国外已有较多研究“信用价差之谜”的相关文献.Chen等[10]通过将宏观经济条件引进到企业的融资决策中,建立了动态资本结构化模型,利用这个模型,作者对“信用价差之谜”和低杠杆之谜给出了基于风险角度的解释.He和Xiong[9]通过展期风险研究了债券市场的流动性和信用风险之间的相互影响.他们的模型表明,债券市场流动性的恶化不仅导致流动性溢价的提高,还会导致企业的信用风险增加,从而提高信用价差.Albagli等[19]则考虑分散信息这个因素,通过发展动态的理性期望均衡模型研究了“信用价差之谜”.
国内也已开展对企业债券及其信用价差的研究.谭地军等[20]对我国企业债券特征与债券风险及风险补偿的关系进行了实证研究.冯宗宪等[21]采用自回归等时间序列模型研究了国内企业债价差的时间序列性质,实证分析了各个期限的企业债券信用价差序列的异方差结构等统计特性.王安兴等[13]通过Nelson-Siegel方法计算国内公司债的价差及税收溢价,并通过时间序列回归分析和横截面回归分析的方法,研究国内公司债价差的构成以及各种外生的因素对价差和价差变化的影响.针对我国债券市场,刘善存等[22]利用遗传算法计算信用价差,并进而建立信用价差的时间序列模型研究信用价差的动态过程.此外,国内对企业债券的研究主要集中在收益率上[23-25],在此不再赘述.
1 一般模型
本文研究无穷界限(infinite-horizon)的连续时间代理问题.假定在经济系统中存在3个参与者:企业股东、企业债券持有人及代理人,其中股东与债券持有人是投资者.企业股东作为委托人雇佣职业经理(即代理人)运营企业.假设投资者与代理人均是风险中性的,并且他们的收益贴现率是无风险利率r.同时,代理人具有有限责任且无初始现金,股东能够承担所有损失成本并且也是有限责任.类似于文献[14-15]等,假设企业的基础价值{Vt∶0≤t<∞}服从几何布朗运动(Geometric Brownian motion)
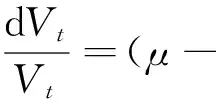
(1)其中常值μ是资产的期望收益率;φ是企业固定的红利支付比例;σ是资产价值的波动率;{Zt∶0≤t<∞}是标准布朗运动,代表着企业资产价值受到的随机冲击.
与Leland和Toft[15]以及He和Xiong[9]相同,本文假设企业具有稳定债务结构(stationary debt structure),记之为(C,P,m).即在任意时刻,企业发行债券的总本金为P,年化支付的票息(简记为票息)为C,每个债券的债务期限是m,并且距离债券到期日的时间均服从一致概率分布.这意味着在时间区间(t,t+dt]内,有dt/m比例的债券到期并且需要展期.换句话说,当一个债券到期时,企业将通过发行一个新的债券来代替它,且新发行的债券具有与之相同的债券期限、本金和票息.将企业发行的债券分为m组,这样每一组具有本金p=P/m和票息c=C/m,这些债券之间的唯一区别是距离债券到期日的时间τ∈[0,m]不相同.将d(Vt,τ)记为其中一组债券的价值,它是基础价值Vt和τ的函数.在本文的分析中,企业的杠杆(即C与P)和债券期限(即m)作为给定的变量对待.
对于债权人,当企业濒临破产时,假设他们从破产清算中能够得到企业资产的α(<1)部分,损失的企业资产便是破产成本.此外,记企业的违约破产时刻为T=inf{t≥0∶Vt≤VB},这里,VB是给定的违约边界.
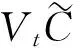
代理人是否尽职工作将决定企业不同程度的风险防范水平,进而影响大规模损失发生的概率,即代理人尽职工作会降低大规模损失在(t,t+dt]内的发生概率Λtdt.为了简单起见,本文只考虑两种工作努力程度:尽职工作与卸责,它们分别对应Λt=λ和Λt=λ+Δλ,其中λ>0,Δλ>0.如果代理人的工作努力程度不能够被股东观察到,便会导致道德风险问题以及由此产生的代理成本.为了描述不同努力程度产生的成本,本文采用与Holmstrom 和 Tirole[26]相同的方式:若代理人在t时刻卸责,即Λt=λ+Δλ,他将得到私人收益VtB,这里B是规模调整的私人收益;相反的,若代理人在t时刻尽职工作,即Λt=λ,他将没有私人收益.从现在起,本文考虑代理人是否卸责不能够被股东观察到的情形.这样,便会导致道德风险问题的产生,而其涉及的关键参数是B与Δλ:规模调整的私人收益B越大,代理人卸责的动力越大;Δλ越小,辨别代理人是否卸责的难度越大.
为了降低大规模损失发生的概率并且激励代理人尽职工作,股东与代理人之间事先签订具有激励性质的长期合约,并且假定双方都完全接受.代理人针对这个合约将选择自己的努力程度过程Λ={Λt}t≥0.假定合约规定了代理人的收入除了基本收入外还有额外的奖金Vtδt,这里,δt是t时刻的规模调整奖金额度*通常情况下,在合约期限内基本收入是不变的,不失一般性,为了简化分析,假设基本收入为零..但是只有在t时刻大规模损失没有发生的情况下,股东才会向代理人支付奖金.因而,在(t,t+dt]时间内代理人的收入为
Vtδt1{dNt=0}dt+VtB1{Λt=λ+Δλ}dt
(2)
其中第1项为股东支付的奖金,第2项为代理人卸责时得到的私人收益.为了叙述方便,记dKt=Vtδt1{dNt=0}dt.这样,代理人与股东签订的就是关于δt的合约,记为Γ={δt}t≥0.此外,由于代理人是在知道大规模损失是否发生之前选择努力程度的,因此形式上,Λ是-可预测的,这里={t}t≥0是由点过程N生成的σ-域流.
为了简化分析,假定企业资产的收益被立刻支付给股东,并且任何的损失都将通过发行更多的股票来弥补.因此,当大规模损失发生时,企业将通过发行额外的股票来偿清损失,以防止企业破产,但这会降低现有股票的价值.由前面的叙述可知,t时刻股东将支付给代理人奖金Vtδt1{dNt=0}.由此,在时间区间(t,t+dt]内,股东得到的净现金流为
Vtφdt-C(1-π)dt-
(3)
其中π是企业税率.这样,大规模损失造成的成本及股东支付给代理人的奖金都将反馈到股权价值中.当企业的资产价值降到内生违约边界VB时,股权价值降为零,此时企业违约,债权人将得到企业的清算价值αVB.
在给定合约Γ={δt}t≥0以及努力过程Λ的条件下,股东的期望收益是
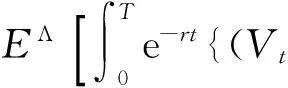
(4)
同时代理人的期望效用是
(5)
这里,EΛ是在由努力过程Λ产生的唯一概率测度PΛ下的期望算子.一个努力过程Λ关于合约Γ称为是激励相容的,如果在给定Γ的情况下,该努力过程使得代理人的期望效用式(5)最大化.在动态道德风险存在的情况下,股东面临的问题便是找到一个合约Γ和激励相容努力过程Λ,并且最大化其期望收益式(4).在连续时间合约模型框架下,在下一节求解出最优合约Γ.在此基础上,将该最优合约代入到股权价值的定价中去,从而分析股东与代理人之间存在的道德风险对企业信用风险和信用价差的影响.
2 最优激励合约
本节将求解动态道德风险存在下的最优激励合约,为此需要首先给出激励相容条件.
2.1激励相容条件
利用鞅(martingale)方法刻画激励相容条件.在给定合约Γ的情形下,当代理人在t时刻做出工作努力水平的决定时,他会考虑该决定将如何影响其自身的连续效用(continuation utility)
Wt(Γ,Λ)=
(6)
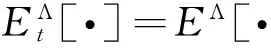
Ut(Γ,Λ)=
e-rtWt(Γ,Λ)
(7)
由式(7)知,U(Γ,Λ)={Ut(Γ,Λ)}t≥0在测度PΛ下是一个鞅.因此,利用鞅表示定理,可以给出U(Γ,Λ)的另外一种表达形式.考虑随机过程
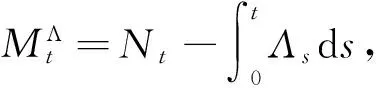
(8)
Ut(Γ,Λ)=U0(Γ,Λ)-
(9)
对式(7)求全微分,再由式(8)和式(9)得到代理人的连续效用满足如下随机微分方程
dWt=[rWt-1{Λt=λ+Δλ}VtB]dt+
Ht(Λtdt-dNt)-dKt
(10)
由式(10)可知,Ht(Γ ,Λ)是代理人的连续效用对大规模损失的敏感度,而当去掉代理人的私人收益和奖金时,其连续效用的期望变化率就等于其收益贴现率r.基于上述分析,能够得到和文献[18]性质2相似的激励相容条件,即下面的引理1.
引理1给定合约Γ={δt}t≥0,则工作努力过程Λ是激励相容的充分必要条件是:对于任意时刻t∈[0,T],Λt=λ成立当且仅当
Ht(Γ,Λ)≥Vtb
(11)
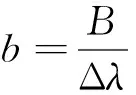
引理1的证明与文献[18]性质2的证明相同,详细证明过程请读者参见文献[18].
由式(10)可知,如果在t时刻发生大规模损失,那么代理人的连续效用将减少Ht(Γ ,Λ).引理1表明,为了促使代理人选择尽职工作提高风险防范水平,以降低大规模损失发生的概率,其连续效用的减少应不低于Vtb.这是因为卸责对代理人的吸引程度可被Vtb体现出来.令ht=Ht/Vt,则在Λt=λ下的激励约束条件式(11)可重新写为
ht≥b
(12)
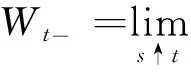
2.2最优合约
为了求解出最优合约,首先需要给出委托人(股东)在t时刻的连续效用
(13)
所满足的微分方程.
由于委托人的收益贴现率是r,因此在t时刻,其连续效用在t+dt时刻的期望值是rF(Vt,Wt-)dt,在无套利均衡状态下,这个值一定等于期望现金流和其连续效用的期望变化率之和.前者等于委托人在区间[t,t+dt]上的期望现金收益减去期望代理成本,即
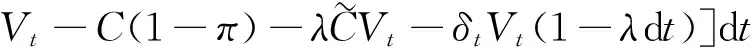
(14)
而委托人连续效用的期望变化率是E[dF(Vt,Wt-)].为了计算式期望变化率,利用代理人连续效用满足的随机微分方程式(10),并令其中的Λt=λ,应用关于Levy过程的Ito公式得到
E[dF(Vt,Wt-)]=FVVt(μ-φ)dt+
FW[rWt+λHt-Vtδt(1-λdt)]dt+
λ[F(Vt,Wt-Ht)-F(Vt,Wt-)]dt
(15)
这样,根据连续效用在t+dt时刻的期望值等于式(14)与式(15)之和,再令dt→0,可得到委托人的连续效用函数满足如下的HJB方程
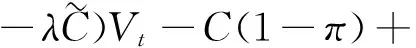
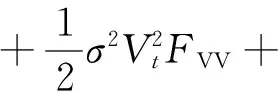
λ[F(Vt,Wt-Ht)-F(Vt,Wt-)]}
(16)
式中所要求解的最优控制变量ht和δt需要满足条件式(12)和δt≥0.
为了更深入地了解方程(16)解的结构,求解出最优合约{δt}t≥0,需要对函数F(V,W)做出进一步的限制:F(V,W)是关于代理人的连续效用W的凹函数*Sannikov[28]和 Biais等[18]分别对于连续情形和跳跃情形严格证明了委托人的连续效用函数F关于代理人的连续效用W是凹函数.本文建立的模型是文献[18]讨论情形的一种特殊情况,故在此省略证明,详细证明可参见该文献性质2的证明过程..这就表明,在HJB方程(16)中,最优的ht(或Ht)应尽量小,再由激励相容条件式(12)(或式(11))可知最优的ht是
(17)
在得到最优的ht后,下面开始求解最优合约.对于代理人,若其在任意时刻t∈[0,T]尽职工作,则没有私人收益VtB.在这种情况下,由于已经假设企业不会推迟发放奖金,因而无论代理人的连续效用Wt多大,当没有大规模损失发生(即dNt=0)时,代理人会立刻获得奖金,即其得到的现金流大于零,否则代理人得到的现金流为零.因此,利用前面推导方程(16)的方法,可得到代理人连续效用的期望变化率不大于其收益贴现率r,即
EΛ[dWt]≤rWtdt
(18)
这样,当大规模损失没有发生时,由方程式(10)和式(18)便可得到
λhtVt-δtVt≤0
(19)
由方程(16)及F关于W的凹性可知最优的δ应尽量小,再由条件式(19)得到最优合约δt满足
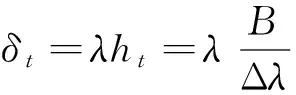
通过上面的分析,可得到下面的引理.
引理2对于任意的时刻t∈[0,T],在没有大规模损失发生的情况下,委托人与代理人签订的最优合约是
(20)
式(20)表明,代理人得到的奖金与规模调整的私人收益B和大规模损失发生的概率λ成正比,与Δλ成反比.事实上,Δλ越小表明委托人发现代理人卸责的难度越大,因而,为了鼓励代理人尽职工作,当Δλ越小时,委托人必须用较多的奖金才能够激励代理人尽职工作.而私人收益的多少将决定委托人给予代理人的奖金多少,如果奖金不如私人收益更有吸引力,则代理人将很有可能在工作时卸责.此外,Poisson风险发生的概率越大,代理人自然需要得到更多的奖金以被激励尽职工作,从而提高其风险防范水平.
3 定价与内生违约边界
在考虑道德风险存在的情形下,得到了股东与代理人的最优合约*严格地讲,第2部分得到的合约式(20)需要验证性定理(verification theorem)以证明其是最优合约.但利用文献[18]性质3的证明方法可以证明该验证性定理,由于证明过程大致相同,在此省略证明..下面将研究道德风险对于企业债券的信用价差是否产生影响,若有影响,道德风险将如何影响信用价差.在此之前,为了方便下面的分析,需要对基础价值Vt满足的随机微分方程(1)进行一个技术上的处理.根据Girsanov定理*参见文献[29]第5章定理5.2.3.,可知Vt在风险中性(risk-neutral)概率测度P下满足如下的随机微分方程
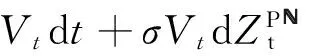
(21)
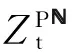
3.1债券价值
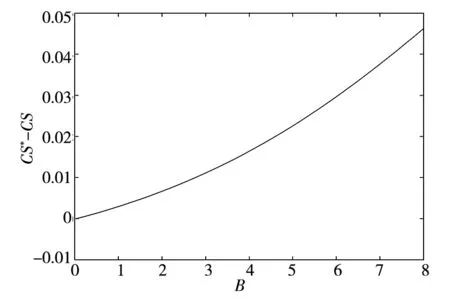
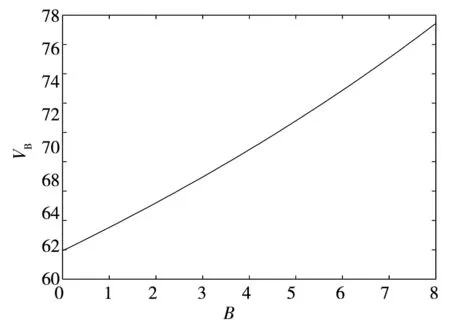
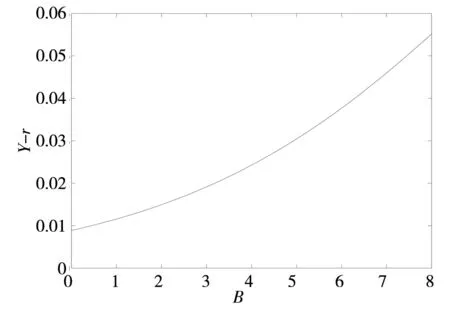
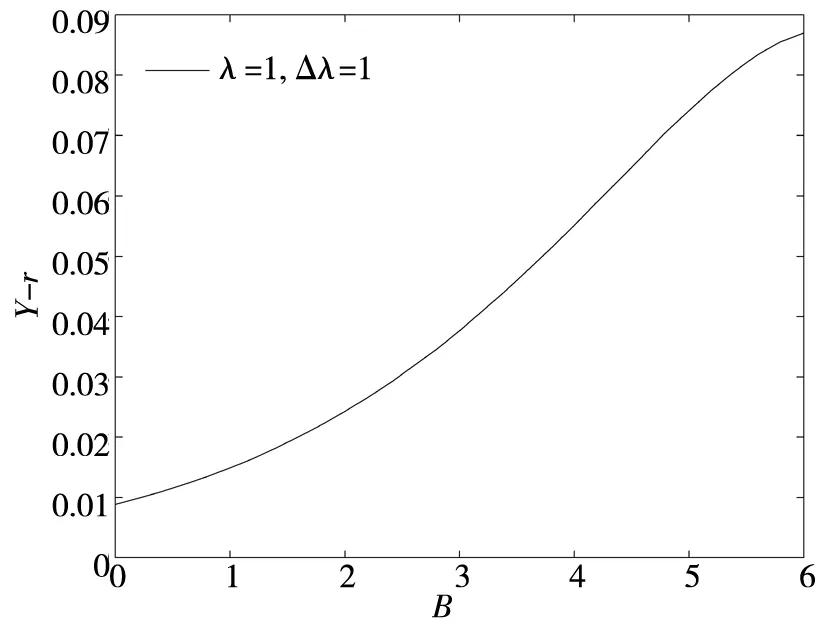
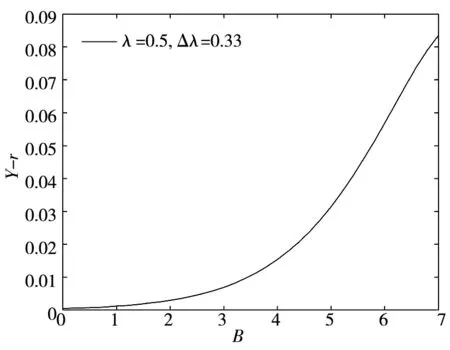
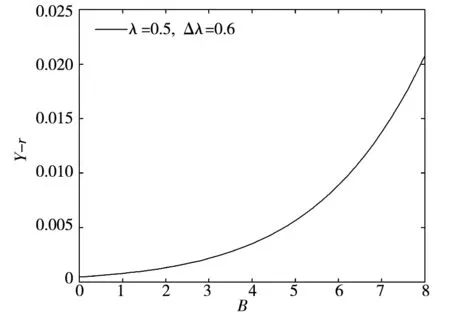
首先在假定违约边界VB给定的情况下,对企业债券进行定价.正如在第1部分中所述,d(Vt,τ;VB)是距离到期日的时间为τ (22) 式中等号左侧的rd(Vt,τ)是持有债券的期望收益;而等号右端的第1项是持有债券的期望现金流;最后3项表示债券价格随着基础价值Vt的波动而出现的预期变化. 为了求解出方程(22),需要两个边界条件.如前所述,当基础价值Vt处于违约边界VB时,债券持有者将获得企业清算后的资产价值αVB.这样,每一组债券在清算时的价值为 (23) 当τ=0时,债券到期,且若企业没有破产,那么债券持有者将得到本金p,即 d(Vt,0;VB)=p, ∀Vt>VB (24) 由边界条件(23)和(24),可以解析求得方程(22)的解 (25) 其中 (26) 在连续支付票息的情形下,给定由微分方程(22)得到的债券价格,债券的收益率可以从如下方程中求得 (27) 式中右端是基于到期日之前没有违约或者没有交易发生的条件下,本金为p且票息为c的债券价格.债券收益率Y与无风险利率r之间的价差Y-r即为债券的信用价差.由于债券价格受违约边界VB的影响,且通过下面的分析可知,VB会受到道德风险的影响,因而道德风险将影响信用价差.下面关注道德风险是如何影响企业债券的信用价差. 3.2股权价值与内生违约边界 为了求得信用价差,必须得到违约边界VB,而VB是由股权价值f(V)内生决定的.在以往文献中, Leland和Toft[15]及Chen和Kou[30]等都是间接地通过将企业总价值减去债券价值得到股权价值.企业总价值是企业的资产价值加上税盾收益,再减去企业的破产成本后得到的.然而在本文中,通过这个等式不能得到股权价值.这是因为,企业的价值被未来的损失成本和支付给代理人的奖金消费掉.这样,需要通过微分方程来直接求得股权价值.在最优合约得到的基础上,可得到股权价值f(Vt)满足如下的微分方程 (28) 对于方程(28)的求解,需要两个边界条件.由于股东具有有限责任,因此能够得到第1个边界条件f(VB)=0;再由平滑黏性条件(smooth-pasting condition),可得到第2个边界条件fV(VB)=0,其中VB是待求解的内生违约边界*对于包括有限债务期限和企业的资产价值服从跳跃-扩散过程在内的一般条件,Chen和Kou[30]在内生违约模型下严格证明了平滑过渡条件是成立的..本文将利用拉普拉斯变化求解方程(28),详细求解过程参见附录. 下面的性质1给出了关于股权价值和内生违约边界的解析表达式. 性质1股权价值f(Vt)由下式给出 (29) 内生违约边界VB是 (30) 如前诉述,B/Δλ表示对代理人选择卸责的吸引程度,λdt是在[t,t+dt]区间内大规模损失发生的概率.因此,根据性质1的结论,在其它参数固定不变的情况下,当因卸责而得到的私人收益B提高时,企业的违约边界 后面的数值分析表明,通常情况下,违约边界VB越大(但不超出一定的数值范围),则企业的违约概率越高,企业债券的信用价差也就因此越大.对于不同行业的企业,其自身所在行业的特征决定了B、λ及Δλ不尽相同,而这些都是道德风险问题涉及的关键参数.因此,道德风险问题不仅对企业债券的信用价差产生了影响,而且不同领域的企业中存在的道德风险问题对各自发行债券的信用价差的影响程度也各不相同.这对于理解不同行业的企业债券的价格差异是有帮助的.同时,对于企业债券发行和交易时的价格合理制定也具有重要的指导意义. 在对模型进行系统的理论分析之后,本节将通过数值计算量化分析道德风险对信用价差产生的影响,从而从道德风险的角度解释“信用价差之谜”. 4.1模型参数设置 表1 基本参数设置 4.2信用价差 为了分析道德风险对信用风险是否有影响,首先分别计算代理成本存在与不存在时的信用价差.采用表1中的基本参数值,并令规模调整的私人收益B取值为0~8‰,对于同一债券,图1展示了代理成本(私人收益)存在时的信用价差(记为CS*)和不存在时的信用价差(记为CS)的差别.具体的,如果私人收益B从0.1%增加到0.8%,对于债务期限为1年的债券,本文得到的信用价差大于Leland和Toft[15]模型得到的信用价差,且增幅从33个基点增加到465个基点.因而,在考虑道德风险的情形下,信用价差明显大于不考虑道德风险的情形,且随着代理成本的增加,两种情形下的信用价差的差距不断扩大. 再将表1中的基本参数值代入到式(25)、式(27)和式(30)中,可以量化分析道德风险对信用价差的影响程度.图2展示了在其它参数不变的情况下,私人收益B的增长对内生违约边界和信用价差的影响.由图2a)可知,当私人收益B增加时,违约边界会随之提高,说明企业内生违约边界VB与B是正相关关系;图2b)则展示了当私人收益B增加时, 债券的信用价差随之非线性增加,且增加幅度逐步提升.更进一步,从 B组可知,当B从0.1%增加到0.8%时,信用价差从120个基点增加到552个基点. 从图1和图2可以知道,在考虑代理问题的情况下,债券的信用价差相对于不考虑道德风险的情形会有明显的提高,且随着代理成本(如私人收益B或卸责吸引程度B/Δλ)的增加,信用价差增加的幅度不断扩大.而对于研究信用价差的已有相关文献,都没有考虑道德风险这个因素.这样,从代理人和股东之间存在道德风险问题(更广泛的是代理问题)这个角度,本文对“信用价差之谜”给出了合理解释. 图1 道德风险对信用价差的影响 a) b) 对于不同的行业,大规模损失发生的概率λ、辨别卸责的难度Δλ以及损失的成本都不尽相同.例如,对于制造业和金融业,由于金融业的随机性和金融资产价值的波动较大,而制造业的生产相对平稳,因而在两个行业的企业中,代理人卸责对大规模损失发生概率的影响程度明显不同.考虑跳跃(即Poisson风险发生)次数适度和很少两种情形,令跳跃强度分别为λ=1和λ=0.5.图3表明λ和Δλ的取值不同,产生的信用价差也不相同.具体的,a)图取λ=1,Δλ=1表示大规模损失发生次数适度;b)图取λ=0.5,Δλ=0.33;c)图取λ=0.5,Δλ=0.6,后两者表示大规模损失发生次数很少.在其它参数不变时,由图2b)和图3可知,当私人收益B的取值不是很大时,λ较小则信用价差较小,Δλ较小则信用价差较大,即信用价差与λ成正比,与Δλ成反比.直观的看,λ较大时,表明企业发生大规模损失的概率较高,因而企业违约的概率也较大;Δλ较小时,表明代理人卸责被辨别出的难度较大,这样代理人更倾向卸责,因而企业出现大规模损失的概率相比于较大的Δλ会更高,从而企业发生违约的可能性更大,导致信用价差增加. a) b) c) 通过将代理人与股东之间的连续时间最优合约模型嵌入到内生违约结构化框架中,本文建立了可以量化分析的理论模型,研究道德风险对信用风险和信用价差的影响.该模型表明,考虑道德风险得到的信用价差显著大于不考虑道德风险的情形.理论和数值分析表明,刻画道德风险的相关参数,包括规模调整的私人收益、辨别代理人卸责的难度以及大规模损失发生的概率,都对信用价差产生不同程度的影响.因此,考虑代理成本,本文的模型对“信用价差之谜”提供了一个合理解释.进一步,论文的相关量化结果可用于信用衍生品的定价研究中,拓展了信用风险的研究内容.同时,通过本文的研究,认识到管理道德风险对于企业运营的重要性,更重要的是使企业能够找到具体的参数目标来管理道德风险问题.此外,本文的模型还能够分析考虑道德风险时企业的最优资本结构,帮助企业做出融资决策,提高企业经营效率与企业价值,在以后的研究中将在这方面继续探讨. 本文建立的理论模型相对简单,对于分析一般的代理问题对信用风险的影响仅仅是开始,仍有许多方向值得深入研究.例如,本文仅讨论了特殊的代理问题,即道德风险问题,但对于一般的代理问题,尚无法解决;对于本文的理论结果,今后还需要进行深入地实证研究.这些都是今后需要研究的内容. [1]Huang J, Huang M. How much of the corporate-treasury yield spread is due to credit risk?[J]. Review of Asset Pricing Studies, 2012, 2(2): 153-202. [2]Jones E P, Mason S P, Rosenfeld E. Contingent claims analysis of corporate capital structures: An empirical investigation[J]. Journal of Finance, 1984, 39(3): 611-625. [3]Duffie D, Singleton K. An econometric model of the term structure of interest-rate swap yields[J]. Journal of Finance, 1997, 52(4): 1287-1381. [4]Feldhuuter P, Lando D. Decomposing swap spreads[J]. Journal of Financial Economics, 2008, 88(2): 375-495. [5]Ericsson J, Rnault O. Liquidity and credit risk[J]. Journal of Finance, 2006, 61(5): 263-286. [6]Longstaff F, Mithal S, Neis E. Corporate yield spreads: Default risk or liquidity? New evidence from the credit default swap market[J]. Journal of Finance, 2005, 60(5): 2213-2253. [7]Chen L, Lesmond D, Wei J. Corporate yield spreads and bond liquidity[J]. Journal of Finance, 2007, 62(1): 119-149. [8]Chen H. Macroeconomic conditions and the puzzles of credit spreads and capital structures[J]. The National Bureau of Economic Research, 2010, 65(6): 2171-2212. [9]He Z, Xiong W. Rollover risk and credit risk[J]. Journal of Finance, 2012, 67(2): 391-429. [10]Chen L, Collin-Dufresne P, Goldstein R S. On the relation between the credit spread puzzle and the equity premium puzzle[J]. Review of Finance Studies, 2009, 22(9): 3367-3409. [11]Bernanke B, Gertler M. Agency costs, net worth, and business fluctuations[J]. American Economic Review, 1989, 79(1): 14-31. [12]Collin-Dufresne P, Goldstein R S, Martin J S. The determinants of credit spread changes[J]. Journal of Finance, 2001, 56(6): 2177-2207. [13]王安兴, 解文增, 余文龙. 中国公司债利差的构成及影响因素实证分析[J]. 管理科学学报, 2012, 15(5): 32-41. Wang Anxing, Xie Wenzeng, Yu Wenlong. Empirical research on China’s corporate bond yield spread[J]. Journal of Management Sciences in China, 2012, 15(5): 32-41.(in Chinese) [14]Leland H. Corporate debt value, bond covenants, and optimal capital structure[J]. Journal of Finance, 1994, 49(4): 1213-1252. [15]Leland H, Toft K B. Optimal capital structure, endogenous bankruptcy, and the term structure of credit spreads[J]. Journal of Finance, 1996, 51(3): 987-1019. [16]He Z. A model of dynamic compensation and capital structure[J]. Journal of Financial Economics, 2011, 100(2): 351-366. [17]Black F, Cox J. Value corporate securities: Some effects of bond indenture provisions[J]. Journal of Finance, 1976, 31(2): 351-367. [18]Biais B, Mariotti T, Rochet J-C, et al. Large risks, limited liability, and dynamic moral hazard[J]. Econometrica, 2010, 78(1): 73-118.[19]Albagli E, Hellwig C, Tsyvinski A. Dynamic Dispersed Information and the Credit Spread Puzzle[R]. Yale University, 2014. [20]谭地军, 田益祥, 黄文光. 中国企业债券特征和风险补偿[J]. 数量经济技术经济研究, 2008, 25(2): 74-87. Tan Dijun, Tian Yixiang, Huang Wenguang. Characteristics and risk premium in Chinese corporate bond market[J]. The Journal of Quantitative & Technical Economics, 2008, 25(2):74-87. (in Chinese) [21]冯宗宪, 郭建伟, 孙克. 企业债的信用价差及其动态过程研究[J]. 金融研究, 2009, (3): 54-71. Feng Zongxian, Guo Jianwei, Sun Ke. Dynamic process of credit spreads of corporate bonds[J]. Journal of Finance Research, 2009, (3): 54-71.(in Chinese) [22]刘善存, 牛伟宁, 周荣喜. 基于SV模型的我国债券信用价差动态过程研究[J]. 管理科学学报, 2014, 17(3): 37-48. Liu Shancun, Niu Weining, Zhou Rongxi. Research on the dynamic process of credit spreads of China’s bonds based on SV model[J]. Journal of Manangement Sciences in China, 2014, 17(3): 37-48. (in Chinese) [23]林海, 郑振龙. 利率期限结构研究评述[J]. 管理科学学报, 2007, 10(1): 79-84. Lin Hai, Zheng Zhenlong. Term structure of interest rate: Selected literature review[J]. Journal of Management Sciences in China, 2007, 10(1):79-84. (in Chinese) [24]范龙振, 张处. 中国债券市场债券风险溢酬的宏观因素影响分析[J]. 管理科学学报, 2009, 12(6): 54-71. Fan Longzhen, Zhang Chu. Explanation of macroeconomic variables on bond risk premium in China[J]. Journal of Management Sciences in China, 2009, 12(6): 54-71.(in Chinese) [25]胡海鹏, 方兆本. 中国利率期限结构平滑样条拟合改进研究[J]. 管理科学学报, 2009, 12(1): 101-111. Hu Haipeng, Fang Zhaoben. Research on improving smoothing spline method to fit China’s term structure of interest rates[J]. Journal of Management Sciences in China, 2009, 12(1): 101-111.(in Chinese) [26]Holmstom B, Tirole J. Financial intermediation, loanable funds, and the real sector[J]. Quarterly Journal of Economics, 1997, 112(3): 663-691. [27]Bremaud P. Point Processes and Queues: Martingale Dynamics[M]. New York, Heidelberg, Berlin: Springer-Verlag, 1981. [28]Sannikov Y. A continuous-time version of the principal-agent problem[J]. Review of Economics Studies, 2008, 75(3): 957-984. [29]Shreve S E. Stochastic Calculus for Finance Ⅱ[M]. New York: Springer, 2004. [30]Chen N, Kou S G. Credit spreads, optimal capital structure, and implied volatility with endogenous default and jump risk[J]. Mathematical Finance, 2009, 19(3): 343-378. 附录: 性质1的证明 证明股权价值满足如下微分方程 (A1) 为了应用拉普拉斯变化方法求解方程(A1),首先做如下的变换v=ln(V/VB),则股权价值f满足 将上述等式代入到方程(A1)中,便得到如下方程 (A2) 且满足边界条件f(0)=0和fv(0)=l.这里,参数l由边界条件,即当v→∞时f(v)关于v是线性的所决定. 由拉普拉斯变换的定义可知L[fv]=sF(s)-f(0)=sF(s)及L[fvv]=s2F(s)-l.这样,可得到 即 (A3) (A4) 由式(A3)和式(A4)可得到 (A5) 对方程(A5)做拉普拉斯逆变换可以得到 (A6) 对于f(v),需要考虑当v→∞时,股权价值关于v将是线性增长的.因为η>1且eηv=(V/VB)η,为了避免股权价值超线性增长,式(A6)中所有含eηv项的系数之和须为零.这样便有 即 (A7) 通过方程(A7)便可以解得参数l. (A8) 最后,由平滑条件fV(VB)=0,或者fV(0)=l=0,利用式(A8)求得内生违约边界 即式(30),结论得证. Agency costs and credit spread puzzle NIU Hua-wei1, 2 1. School of Finance, Nanjing Audit University, Nanjing 211815, China;2. Jiangsu Key Laboratory of Financial Engineering, Nanjing Audit University, Nanjing 211800, China As an endogenous factor, the agency problem may deteriorate the firm’s credit risk. In this paper, the optimal contracting between the agent and equity holders is embed into the Leland-Toft endogenous default model to study the impact of moral hazard on credit risk and credit spreads. Our model shows that the agency cost induced by moral hazard can have significant impacts on credit spreads. The credit spreads are obviously larger when the moral hazard problem is considered, and our model highlights the role of the key parameters of the moral hazard in affecting the credit spreads. Thus the moral hazard could be used to explain the credit spread puzzle. The explicit formulae of the equity value and the endogenous bankruptcy barrier are also given. credit spreads; principal-agent; moral hazard; credit risk; Poisson risk 2014-03-05; 2014-12-09. 国家自然科学青年科学基金资助项目(71501099); 江苏省自然科学青年基金资助项目(BK20150725); 江苏省高校自然科学研究资助面上资助项目(15KJB110011); 江苏省金融工程重点实验室开放课题资助项目(NSK2015-01); 江苏高校品牌专业建设工程一期项目金融学资助项目(苏教高[2015]11). 牛华伟(1980—), 男, 江苏徐州人, 博士, 副教授, Email: niuhuawei@gmail.com F830.91; F224 A 1007-9807(2016)08-0054-13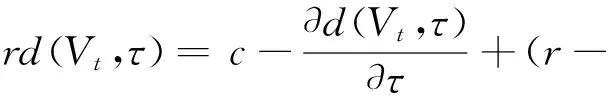
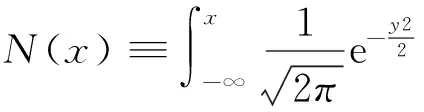
4 道德风险对信用价差的影响
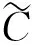

5 结束语