差异分批模式下的联合成本优化问题及算法

程八一， 黄小曼， 杨艳艳， 胡笑旋

(1. 合肥工业大学管理学院， 合肥 230009； 2. 过程优化与智能决策教育部重点实验室, 合肥 230009)



差异分批模式下的联合成本优化问题及算法

程八一1， 2， 黄小曼1， 2， 杨艳艳1， 2， 胡笑旋1， 2

(1. 合肥工业大学管理学院， 合肥 230009； 2. 过程优化与智能决策教育部重点实验室, 合肥 230009)

提出了一类制造企业的联合成本优化问题，将企业的产品制造环节和配送环节进行协同运作，实现供应链环境下的联合调度.在生产环节，考虑一类典型的差异分批制造模式，即待加工的作业尺寸有差异，而批处理设备的容量确定，设备环境为多台并行设备；在配送环节，企业采用自有车辆进行运输，车辆具有相同的运输能力；若完工的作业在当前无可用车辆进行配送，则转入产成品库存；联合成本为生产、库存和配送三阶段的总成本.本文首先构造了基于整数规划的数学模型，证明了联合成本的最小化问题是强NP-hard问题；然后设计了多项式时间的近似算法，分析了算法的时间复杂性，并证明了算法的求解性能.

供应链调度； 联合成本； 差异作业； 近似算法

0　引　言

在当前激烈的市场竞争环境下，制造型企业不再单纯的追求大批量、高速度的生产方式，而是将重点放在提高作业质量、改善客户服务水平等方面，统筹企业的采购、库存、生产与配送环节，获得经济效益的总体优化，从而提升企业的综合竞争力.供应链调度便是从制造企业所在供应链的视角出发，采用精确调度的方法，考虑面向供应链的多环节优化与调度，包括制造企业的原材料采购、生产、库存和配送过程.其思想由Hall和Potts[1]两位学者提出，他们的研究表明，在传统的制造模式下，通过供应链调度的方法，能够将制造企业的总成本降低20%以上.

近年来供应链调度的研究有了较快的进展，很多学者在供应链调度模型的构建以及优化算法的设计方面做了大量的工作.按照供应链调度所涉及的范围可以分为两阶段供应链调度和三阶段调度，其中两阶段调度问题涉及到供应商-制造企业和制造企业-客户这两类模型，三阶段调度则为供应商-制造企业-客户模型.在供应商-制造企业模型中，Chen和Hall[2]和Agnetis等[3]研究了供应商和制造企业最优方案的冲突，分别提出了一类兼顾二者利益的合作机制；Torabi等[4]考虑了供应商和制造企业的原材料库存和配送总成本，提出了优化总成本的智能算法.两阶段供应链调度问题的另一种模型便是制造企业-客户模型，Chen和Vairaktarakis[5]考虑了古典生产模式下的生产与配送调度问题，证明了该模式下优化制造跨度和成本问题均为NP-hard问题，提出了几类启发式算法；由于这类问题的计算复杂性，后期的研究集中在近似算法[6-7]和智能算法方面[8-9]，另外，学者们考虑了两阶段供应链调度问题的现实约束并设计了优化算法，这些约束包括作业保质期极短[10]和生产能力有限[11]等.另一方面，三阶段供应链调度问题，则涉及到原材料设计、生产加工和成品配送三个部分，Hall和Potts[1]系统的构造了该类问题在古典生产模式下的模型，并设计了基于动态规划的优化算法；Selvarajah和Steiner[12]设计了一类优化配送-库存联合成本的近似算法，最坏性能比为1.5；Sawik[13]考虑了一类优化库存、生产和配送总成本的问题，且作业具有很长的生命周期；Yimer和Demirli[14]则提出了一类分解算法，将三阶段问题分解为生产和运输两个子问题，并采用遗传算法进行优化；后期的研究中学者们也考虑了工业中的实际约束，包括带时间窗[15]和同步原料补给[16]的供应链调度问题.

但上述的供应链调度研究均在古典生产模式[17]下展开，这类模式的基本假定，就是加工设备同时生产一个作业或者固定数量个作业，前者称为传统生产模式，后者称为批生产模式.但在现实工业中，大量的生产问题并不属于这类生产模式，例如半导体芯片制造业、陶瓷制造业、食品加工业、金属冶炼业等，以芯片制造业为例，芯片出厂前的最后一道工序是芯片的高温预烧，工序的目的是通过高温处理发现有质量问题的芯片，从而保证出厂芯片的质量.预烧的处理时间长，是其他工序的几倍乃至几十倍，芯片有不同的尺寸和预烧时间，均由客户指定，而预烧炉的容积是确定的，在预烧时，芯片可以分批放在炉中进行，每一批芯片的总体积不能超过炉子的容积，同时，芯片的预烧时间可以大于客户要求的时间，但不能小于这个时间，因此一批芯片的处理时间等于其中芯片的最长处理时间.称这类生产模式为差异分批模式(production with batch-processing machines with arbitrary-size jobs)，在食品加工业、金属冶炼业中，同样有大量的该类问题.1994年，Uzsoy[18]提出了差异分批模式的单设备调度问题，证明了单设备的制造跨度最优化问题是强NP-hard问题，总完工时间问题是NP-hard问题，并分别设计了启发式算法；Zhang等[19]分析了Uzsoy提出的算法的性能，并进一步设计了一种最坏性能比为7/4的MLPT-FF算法；Tang等[20]针对一类考虑原材料库存的差异作业批调度问题设计了近似算法，程八一等[21]和Tang等[22]分别提出了优化流水车间问题的近似算法；文献[23,24]采用了动态规划方法对该问题进行了优化；文献[25]采用了聚类算法进行求解.除近似算法、动态规划算法和聚类算法之外，一些性能优异的智能算法也被引入到差异分批模式的优化调度中，包括遗传算法[26]、模拟退火算法[27]、蚁群算法[28-30]和微粒群算法[31]等.在作业配送方面，Sahin等[32]从经济分析的角度入手，提出了公路、铁路、海上运输等方式的优化组合方法；Rieksts等[33]和Janeiro等[34]将配送和库存环节联合起来，提出了基于库存的配送策略以获得最低的配送成本；Koca和Yildirim[35]考虑了一类特殊的成本结构，采用分级方法优化配送成本，Ghoseti和Ghannadpour[36]则采用了智能优化方法对配送成本进行优化，获得了较理想的实验结果.

但上述差异分批生产模式的研究仅限于车间内的优化调度，配送研究也仅仅针对作业配送环节，并没有立足制造企业的经营决策高度对两者进行协调优化.生产环节的研究主要通过设计生产方案来获得最低的生产成本，配送环节的研究主要是通过对车辆和产成品的获得最低的配送成本，由于两个环节内的优化目标不同，因此两者的简单相加必然不是制造企业的最优策略，这两种优化方案对制造企业的借鉴和参考价值是有限的.尤其是在当前强调企业服务水平的环境下，应对制造企业的生产、库存和配送进行集成思考和系统设计，从企业经营决策的高度给出生产-库存-配送的联合调度策略，获得作业生命周期内从安排加工直至送达客户的一体化运作方案，从而为制造企业提供全面、精细的运作支持.本文采用一类典型的差异分批制造模式，从制造企业的决策角度出发，设计集成化的分批、生产、库存和配送方案，来优化企业的供应点调度总成本.对制造企业来说，生产成本主要包括生产过程的能耗和操作人员工资费用，这些均取决于生产时间的长短；在库存环节，成本包括库存运行成本和人员工资等变动成本，库存成本取决于库存产品总量和库存时间；而在配送环节，成本则主要包括运输中的燃油费用和驾驶员工资，这些均取决于配送路线的长度和运输的次数.首先建立基于上述声明的生产-库存-配送联合成本的供应链调度模型，分析成本优化问题的计算复杂性，然后设计有效的多项式时间算法，实现联合成本的优化，以期为制造企业的运作提供直接有效的借鉴和参考.

1　整数规划模型与计算复杂性

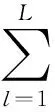
定义下述决策变量

根据上述的问题描述，建立整数规划模型如下

(1)

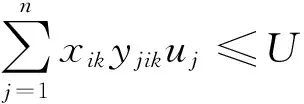
i=1,…,m; k=1,…,Ki

(2)

Tik=max{tj∶yjik=1}

i=1,…,m; k=1,…,Ki

(3)

Ci,h+1-Ti,h+1≥Cih

i=1,…,m; h=1,…,Ki-1

(4)

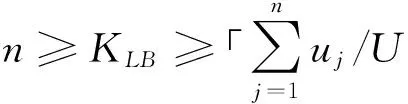
(5)

(6)

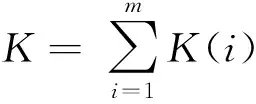
(7)

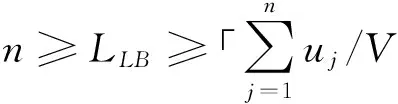
(8)

(9)

(10)

xik,yjik,wl,zjl∈{0,1}∀i,j,k

(11)

模型中，KLB和LLB分别表示总批数K和总配送次数L的下界.目标函数(1)给出了供应链调度总成本的表达式；约束条件(2)要求同一批中的所有作业总体积不能超过设备的容量，式(3)和式(4)要求批的加工不允许中断；式(5)和式(7)分别给出了总批数的上下界以及计算方法，其中「a⎤表示不小于a的最小整数；式(6)利用决策变量求出K(i)；式(8)给出了运输中车次数量的下界，式(9)则利用决策变量wl求出车次数；式(10)要求每一车作业的总体积不能超过车辆的运输能力；式(11)声明模型中的决策变量均为0-1变量.

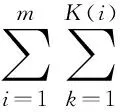
优化目标：最小化箱子的数量；

箱子容积：1；

物品j的体积：uj/U.

而上述装箱问题是强NP-hard问题，因此，有下述结论.

推论1Pm|U,uj,batch|1|v,V|TC是强NP-hard问题.

2　优化算法及其时间复杂性

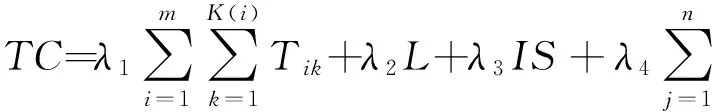
下面给出本文的算法A.

算法A

步骤1将所有作业按照加工时间非增的顺序排序，并重新编号为1, 2,…,n，即有t1≥t2≥…≥tn.

步骤2新建一个空批B1，将作业1放入B1，并将作业1从作业集J中删除；然后从u2开始，逐个将作业j加入B1中，如果总体积仍然不超过U，则j∈B1，若j加入后总体积大于U，则j∉B1，直至所有作业均判断完毕.若此时J≠φ，则新建空批B2，按上述方法组批.重复上述组批过程，直到J=φ为止.此时得到一个可行的批集合Φ = {B1,B2,…,BK}.

步骤3将B1,B2,…,BK按处理时间非增顺序排序，从处理时间最长的批开始，逐个分别安排到M1,M2,…, Mm上加工，同时将这些批从Φ中删除若Φ≠φ，则等到任意设备上有一批作业处理完毕时，将Φ中处理时间最长的批安排到该设备上加工，直至Φ=φ为止，此时所有批次均安排完毕.

步骤4将完工的作业按下述方法分组配送.将Bk(k= 1,…,K)中的作业按任意顺序排列，得到完整的作业序列1, 2,…,n.首先安排第一辆车配送的作业集d1：将作业1放入其中，对后续的所有作业，逐个放入d1，如果总容量不超过V，则j∈d1，否则j∉d1.然后按照该分组方法，依次建立d2,d3,…,dL，直至所有完工作业均安排配送为止.此时得到一个可行的配送方案{d1,d2,…,dL}.若当前批已经完工，且无可用车辆进行配送，则将完工作业转入库存.

在算法A中，步骤1-步骤2完成作业的分批，步骤3完成批次的生产加工，步骤4则获得完工作业的配送方法，故最终获得的可行解π是一个集成化的方案，给出了作业分批、生产和配送的完整过程.下面首先分析算法A的时间性能.

定理1算法A的时间复杂度为O(mn+nlnn).

证明A的时间复杂性可以通过分析4个步骤得到.

步骤1对n个作业排序， 时间复杂性为O(n×lnn).

步骤2等价于First Fit方法[18]求解装箱问题，装箱问题如推论1之前内容所示，由于First Fit算法的时间复杂度为O(nlnn)，故步骤2的时间复杂度为O(nlnn).

步骤3中，对批排序的时间复杂度为O(K×lnK)，由于K≤n，故时间复杂度小于O(nlnn)；在安排加工时，安排前m个批的时间为O(m)，后(K-m)个批中每个批搜索设备的时间为O(m)，故步骤3的时间复杂度为O(m(K-m))，显然不超过O(mn).

步骤4中的配送方法等价于First Fit算法求解下述的装箱问题：物品数量为n；物品j体积为uj/V；箱子的容积为1.而库存算法由生产、配送方案直接产生，其时间复杂度为O(n)，因此，步骤4的时间复杂度为O(nlnn).

综上，通过四个步骤的时间复杂度可知，算法A的时间复杂度为O(mn+nlnn).

证毕.

下面给出具体的算例来说明算法A的求解过程.

3　算　例

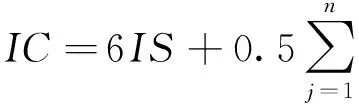
那么根据A的步骤1，将作业按照tj的非增关系排序，可获得排序后的作业序列如表2所示，表的结构与表1相同.

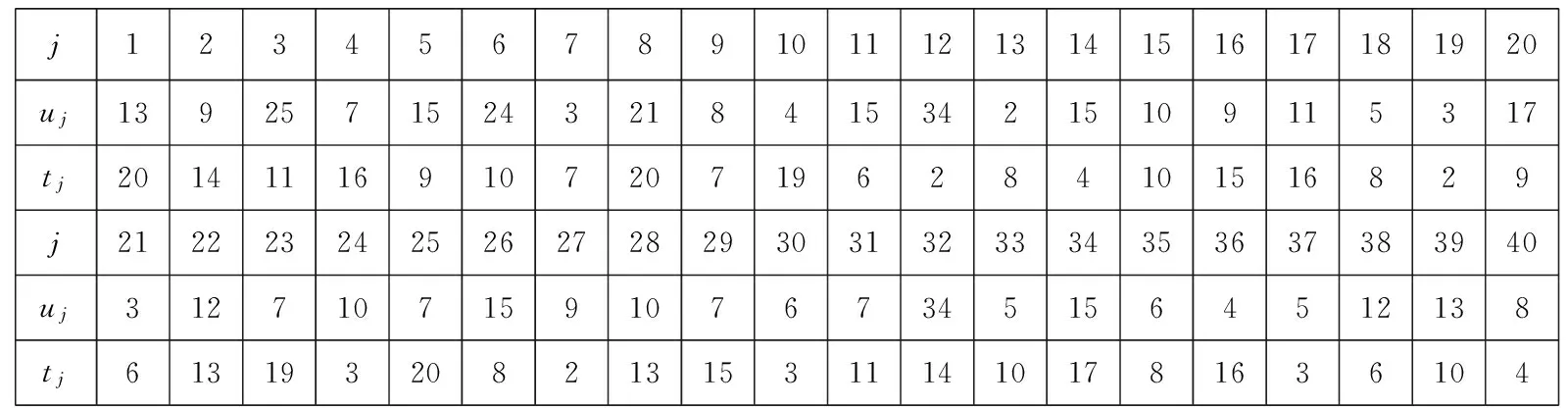
表1　作业尺寸和加工时间

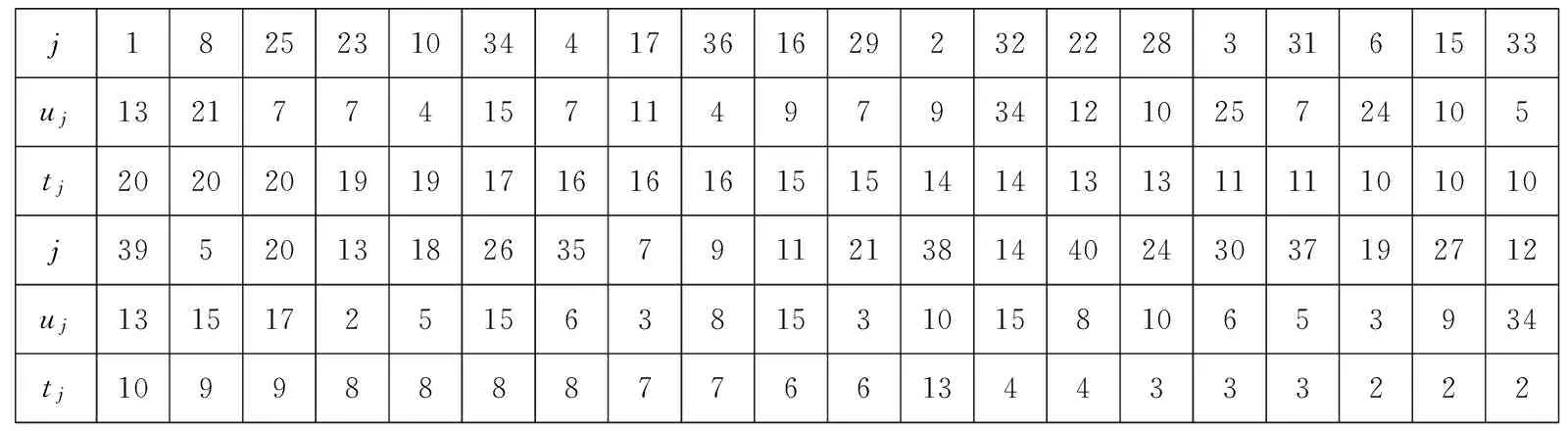
表2　按tj排序后的序列

根据步骤2和步骤3，可以获得如表3所示的分批结果.第一列表示所得的批序列，这些批尚未安排到设备上，记为ei；第二列表示分配到设备上之后的加工情况，可知在设备M1上加工的批集合为{e1,e6,e9}，M2上加工的批集合为{e2,e5,e8}，M3上加工的批集合为{e3,e4, e7}；第三列为每一个批中的作业集；第四列为每个批中作业的总体积，易见b13、b22和b33对设备容量的利用率为98%，而其他6批的利用率则均为100%；第五列表示每个批次的处理时间.

于是，根据PC的计算方法可以获得生产总成本如表4所示.其中第一列表示设备编号，第二列～第七列分别表示设备上的每个批次及完工时间，每台设备上的最后一批作业的完工时间即为设备的运行时间；第八列为每台设备的生产总成本.

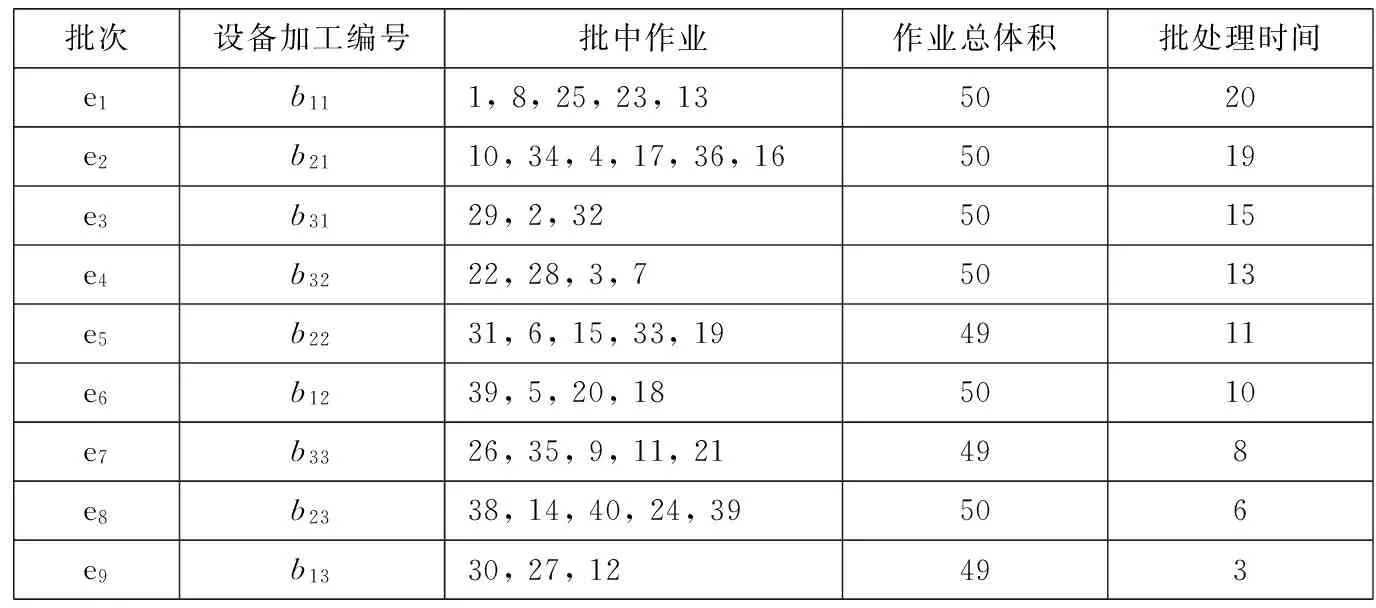
表3　分批结果

表4　设备加工时间与生产成本

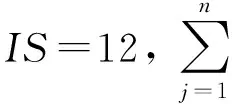
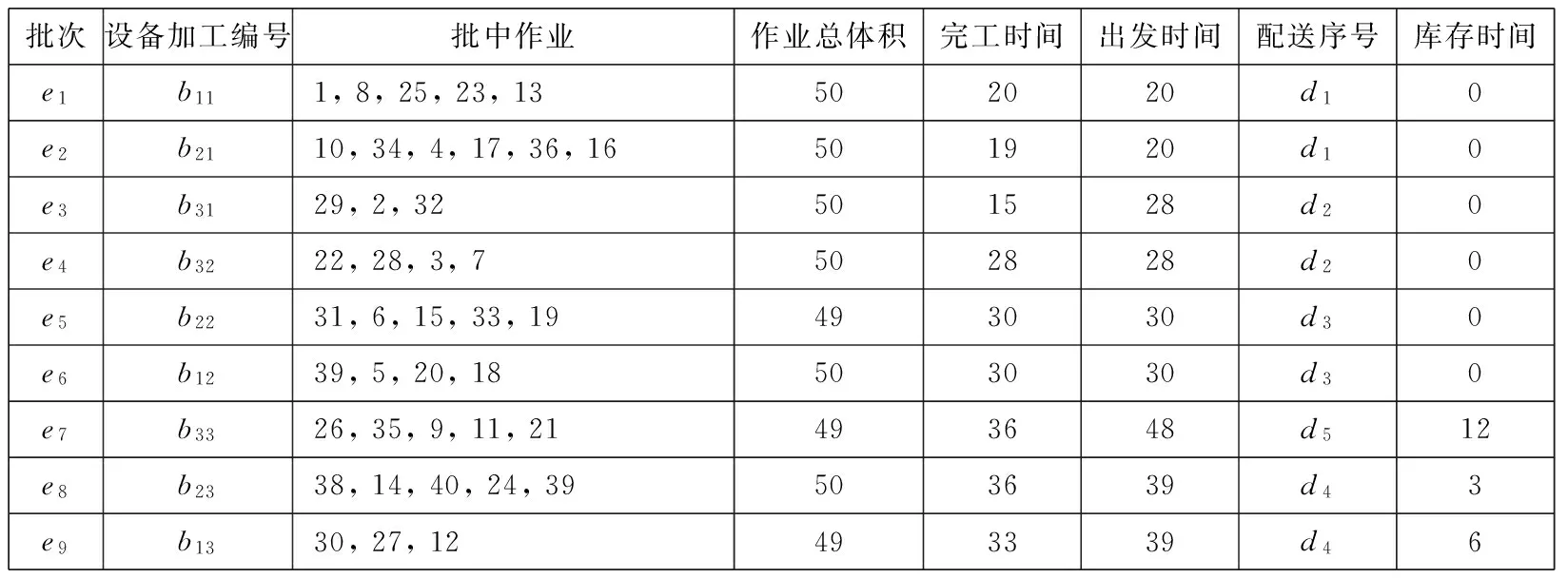
表5　库存方案

综上，算法A产生的联合调度方案总成本TC=PC+IC+DC=3 163.

下面分析A的优化性能，主要指标是A的最坏性能比.

4　优化算法的求解性能

最坏性能比，也即多项式时间算法的近似比，用R表示，对最小化问题来说，算法得出的解与理论最优解的比值即为最坏性能比，比值越接近1，说明算法的优化性能越好.在分析本文算法A的求解性能时，首先从生产环节展开分析.

引理1在生产环节，算法A产生的总批数不超过最优解的两倍.

证明从A的运行过程可以看出，产生分批方案的是步骤1和2.从步骤1和2得知，对任意的整数g,h∈[1,K]且g≠h，有

(12)

若否，则Bg和Bh中的作业可以合并到一个批中，不符合步骤2的要求.现从集合{(g,h)|g+h=K+1}中选择整数对(g,h)，根据式(12)可得

(13)

由于A产生的解π中，所有的作业均分到批中，因此有

(14)

而在最优解π*中，同理有

(15)

根据式(13)-式(15)得

(16)

也即K< 2K*.

证毕.

根据引理1，为了方便后续的证明，在A产生的可行解π中，增加(2K*-K)个虚拟批，所谓虚拟批，即该批的处理时间和作业总体积均为零.这样在π中，生产环节的总批数为2K*个.

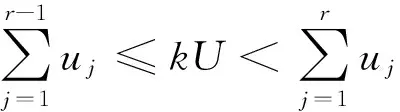
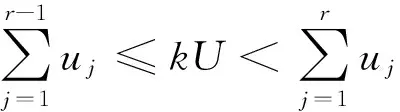
(k-1)U<(r-1)u0≤kU

(17)

结合u0>U/2得到r-1<2k，也即

r< 2k+ 1

(18)

根据式(18)，可知在Ψ2下，作业r分配在了批B1,…,B2k中，由于Ψ1和Ψ2两种情形下的批结构相同，因此在最坏情形Ψ1中，r分配在B1,…,B2k中.故对其他各种情形，r均能分配在前2k批中，引理2得证.

证毕.

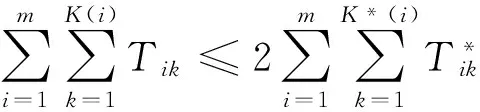
证明先将π和π*中的并行设备问题等价的转换为单设备制造跨度问题，即

(19)

(20)

同理，在最优解π*中，有

(21)

Γ2k+2≤Γ2k+1≤tr

(22)

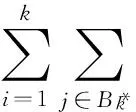
(23)

根据式(22)和式(23)得到

(24)

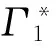
(25)

(26)

根据式(26)， 结合式(19)～式(21)知， 定理1得证.

证毕.

引理3在配送环节，算法A产生的配送成本L< 2L*.

证明算法A中，配送方案的产生在步骤4中.分析步骤4知，A产生的可行车次集{d1,…, dL}满足

∀x≠y and x,y=1,…,L

(27)

从下述集合中选取整数对(x,y)∶{(x,y)|x+y=L+1}，可得

(28)

而最优解π*中，显然有

(29)

证毕.

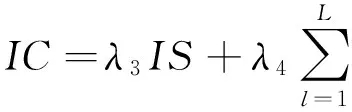
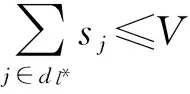
(30)

同时，在库存运行时间方面，有

2IS*=4τL*>2τL=IS

(31)

证毕.

以上对算法的生产环节和配送环节均展开了分析，下面给出算法的求解性能.

定理2在求解Pm|U,uj,batch|1|v,V|TC问题时，算法A的最坏性能比不大于2.

证明根据定理1和引理3、引理4，得到A的性能比如下

=2

定理2得证.

证毕.

5　结束语

本文考虑了制造企业的一类供应链调度问题，在生产环节，制造企业的生产设备为多台并行批处理设备，每台设备有固定的容量，而加工的作业具有任意的尺寸和处理时间，加工时分批进行，每一批作业的加工不允许中断；在配送环节中作业的配送由企业的自有车辆进行运送，车辆具有相同的运输能力；作业加工完毕后，若不能立即配送，则转入产品库存.建立了生产-库存-配送联合成本优化问题的数学模型，证明联合成本的最小化问题是强NP-hard问题，然后提出了一类O(mn+nlnn)时间的近似算法，最坏性能比不大于2.

在后续研究中，本文的供应链调度问题可以根据实际生产扩展为其他设备模型，如流水作业模型、车间作业模型等，由于单设备的供应链调度问题已经是强NP-hard问题，因此流水作业、车间作业模型下的供应链调度问题是强NP-hard问题，对优化算法的研究应集中在近似算法和智能算法两个方面.另外，本文考虑的联合成本优化问题涉及到生产、库存和配送环节，后续研究可以扩展到采购环节，将采购、生产、库存和配送等环节综合考虑，进行系统化建模，并设计有效的优化算法.

[1]Hall N G, Potts C N. Supply chain scheduling: Batching and delivery[J]. Operations Research, 2003, 51(4): 566-584.

[2]Chen Z L, Hall N G. Supply chain scheduling: Conflict and cooperation in assembly systems[J]. Operations Research, 2007, 55: 1072-1089.

[3]Agnetis A, Hall N G, Pacciarelli D. Supply chain scheduling: Sequence coordination[J]. Discrete Applied Mathematics, 2006, 154(15): 2044-2063.

[4]Torabi S A, Ghomi S M T, Karimi B. A hybrid genetic algorithm for the finite horizon economic lot and delivery scheduling in supply chains[J]. European Journal of Operational Research, 2006, 173(1): 173-189.

[5]Chen Z L, Vairaktarakis G L. Integrated scheduling of production and distribution operations[J]. Management Science, 2005, 51(4): 614-628.

[6]Selvarajah E, Steiner G. Batch scheduling in a two-level supply chain： A focus on the supplier[J]. European Journal of Operational Research, 2006, 173(1): 226-240.

[7]Averbakh I, Xue Z. On-line supply chain scheduling problems with preemption[J]. European Journal of Operational Research, 2007, 181(1): 500-504.

[8]Naso D, Surico M, Turchaiano B, et al. Genetic algorithms for supply-chain scheduling: A case study in the distribution of ready-mixed concrete[J]. European Journal of Operational Research, 2007, 177(3): 2069-2099.

[9]Zegordi S H, Abadi I N K, Nia M A B. A novel genetic algorithm for solving production and transportation scheduling in a two-stage supply chain[J]. Compters & Industrial Engineering, 2007, 58(3): 373-381.

[10]Chen Z L, Pundoor G. Order assignment and scheduling in a supply chain[J]. Operations Research, 2006, 54(3): 555-572.

[11]Hall N G, Liu Z. Capacity allocation in supply chains[J]. Operations Research, 2010, 58(6): 1711-1725.

[12]Selvarajah E, Steiner G. Approximation algorithms for the supplier’s supply chain scheduling problem to minimize delivery and inventory holding costs[J]. Operations Research, 2009, 57(2): 426-438.

[13]Sawik T. Coordinated supply chain scheduling[J]. International Journal of Production Economics, 2009, 120(2): 437-451.

[14]Yimer A D, Demirli K. A genetic approach to two-phase optimization of dynamic supply chain scheduling[J]. Computers & Industrial Engineering, 2010, 58(3): 411-422.

[15]Yeung W K, Choi T M, Cheng T C E. Supply chain scheduling and coordination with dual delivery models and inventory storage cost[J]. International Journal of Production Economics, 2011, 132(2): 223-229.

[16]Osman H, Demirli K. Economic lot and delivery scheduling problems for multi-stage supply chains[J]. International Journal of Production Economics, 2012, 136(2): 275-286.

[17]Pinedo M. Scheduling: Theory, Algorithms and Systems[M]. 2nd ed., New Jersey: Prentice-Hall, 2002.

[18]Uzsoy R. Scheduling a single batch-processing machine with arbitrary job sizes[J]. International Journal of Production Research, 1994, 32(7): 1615-1635.

[19]Zhang G, Cai X, Lee C Y, et al. Minimizing makespan on a single batch-processing machine with nonidentical job sizes[J]. Naval Research Lnistics, 2001, 48(3): 226-240.

[20]Tang L X, Gong Hua. A hybrid two-stage transportation and batch scheduling problem[J]. Applied Mathematical Modelling, 2008, 32(12): 2467-2479.

[21]程八一， 胡笑旋. 差异作业批调度的流水车间问题及近似算法[J]. 系统工程学报， 2011, 26(3): 393-399.

Cheng Bayi, Hu Xiaoxuan. Approximation algorithm for scheduling batch processing machines with non-identical job sizes in flow shop[J]. Journal of Systems Engineering, 2011, 26(3): 393-399.(in Chinese)

[22]Tang L X, Liu P. Two-machine flowshop scheduling problems involving a batching machine with transportation or deterioration consideration[J]. Applied Mathematical Modelling, 2009, 33(2): 1187-1199.

[23]Tang L X, Liu P. Minimizing makespan in a two-machine flowshop scheduling with batching and release time[J]. Mathematical and Computer Modelling, 2009, 49(5/6): 1071-1077.

[24]冯大光, 唐立新. 一类新型批处理机调度问题的理论分析[J]. 管理科学学报, 2012, 15(6): 33-48.

Feng Daguang, Tang Lixin. The oretical analysis of scheduling of a new batching machine[J]. Journal of Management Sciences in China, 2012, 15(6): 33-48. (in Chinese)

[25]杜冰, 陈华平, 杨勃, 等. 聚类视角下的差异工件平行机批调度问题[J]. 管理科学学报, 2011, 14(12): 27-37.

Du Bing, Chen Huaping, Yang Bo, et al. Scheduling parallel batching machines with non-identical job sizes from a clustering perspective[J]. Journal of Management Sciences in China, 2011, 14(12): 27-37. (in Chinese)

[26]Damodaran P, Manjeshwar P K, Srihari K. Minimizing makespan on a batch-processing machine with arbitrary job sizes using genetic algorithm[J]. International Journal of Production Economics, 2006, 103(2): 882 -891.

[27]Melouk S, Demodaran P, Chang P Y. Minimizing makespan for single machine batch-processing with arbitrary job sizes using simulated annealing[J]. International Journal of Production Economics, 2004, 87(2): 141-147.

[28]Cheng B Y, Li K, Chen B. Scheduling a single batch-processing machine with arbitrary job sizes in fuzzy environment using an improved ant colony optimization[J]. Journal of Manufacturing Systems, 2010, 29(1): 29-34.

[29]Cheng B Y, Wang Q, Yang S L, et al. An improved ant colony optimization for scheduling identical parallel batching machines with arbitrary job sizes[J]. Applied Soft Computing, 2013, 13(2): 765-772.

[30]王栓狮, 陈华平, 程八一, 等. 一种差异工件单机批调度问题的蚁群优化算法[J]. 管理科学学报, 2009, 12(6): 72-82.

Wang Shuanshi, Chen Huaping, Cheng Bayi, et al. Minimizing makespan on a single batch processing machine with non-identical job sizes using ant colony optimization[J]. Journal of Management Sciences in China, 2009, 12(6): 72-82. (in Chinese)

[31]程八一, 陈华平, 王栓狮. 基于微粒群算法的单机不同尺寸工件批调度问题求解[J]. 中国管理科学, 2008, 16(3): 84-88.

Cheng Bayi, Chen Huaping, Wang Shuanshi. Scheduling a single batch-processing machine with non-identical job sizes based on particle swarm optimization[J]. Chinese Journal of Management Science, 2008, 16(3): 84-88. (in Chinese)

[32]Sahin B, Yilmaz H, Ust Y, et al. An approach for analyzing transportation costs and a case study[J]. European Journal of Operational Research, 2009, 193(1): 1-11.

[33]Rieksts B Q, Ventura J A. Two-stage inventory models with a bi-modal transportation cost[J]. Computers & Operations Research, 2010, 37(1), 20-31.

[34]Janeiro M G, Jurado I G, Meca A, et al. A new cost allocation rule for inventory transportation systems[J]. Operations Research Letters, 2013, 41(5): 449-453.

[35]Koca E, Yildirim E A. A hierarchical solution approach for a multicommodity distribution problem under a special cost structure[J]. Computers & Operations Research, 2012, 39(11): 2612-2624.

[36]Ghoseti K, Ghannadpour S F. Multi-objective vehicle routing problem with time windows using goal programming and genetic algorithm[J]. Applied Soft Computing, 2010, 10(4): 1096-1107.

[37]Chen Z L. Integrated production and outbound distribution scheduling: Review and extensions[J]. Operations Research, 2010, 58(1): 130-148.

Algorithm for minimizing joint cost for manufacturers with batching machines and arbitrary-size jobs

CHENG Ba-yi1, 2, HUANG Xiao-man1, 2, YANG Yan-yan1, 2, HU Xiao-xuan1, 2

1. School of Management, Hefei University of Technolny, Hefei 230009, China；2. Key Laboratory of Process Optimization and Intelligent Decision-making, Hefei 230009, China

A class of problems for manufacturers are proposed to minimize joint cost. Production and outbound distribution are combined to achieve a joint scheduling in supply chain. In the production process, the manufacturers have identical parallel batching machines to process arbitrary-size jobs. The machines have a fixed capacity in size and the total size of jobs in a batch cannot exceed the machine capacity. In the distribution process, the manufacturers deliver the products using their own vehicles and the vehicles have identical transport capacities. If there are no available vehicles to deliver the products, they should be put in inventory. The total cost consists of the production cost, the distribution cost and inventory cost. An integer programming model of the problem is presented and the problem under investigation is shown to be NP-hard in the strong sense. Then a polynomial time algorithm is provided. The time complexity and performance guarantee of the proposed algorithm are analyzed.

supply chain scheduling; joint cost; arbitrary-size jobs; approximation algorithm

2013-06-04；

2015-10-30.

国家自然科学基金资助项目(71202048; 71471052; 71521001); 教育部人文社会科学基金资助项目(13YJC630051).

程八一(1981—)， 男， 安徽安庆人， 博士， 副教授. Email： bycheng@mail.ustc.edu.cn

TP301

A

1007-9807(2016)08-0102-11