基于交叉口复杂度的交叉口秩序模型

李文勇,余子威,王 涛,贺军杰,李佳杰

(1.桂林电子科技大学建筑与交通工程学院， 广西桂林541004；2.北京交通大学交通运输学院， 北京100044)



基于交叉口复杂度的交叉口秩序模型

李文勇1,余子威1,王 涛1,贺军杰1,李佳杰2

(1.桂林电子科技大学建筑与交通工程学院， 广西桂林541004；2.北京交通大学交通运输学院， 北京100044)

针对当前交叉口评价指标仅以交叉口服务水平为准，不能切实反映交叉口秩序水平的情况，通过借鉴交叉口复杂度模型，分析交叉口在不同车道配置、信号配时条件下的合流、分流、交叉冲突点数值关系，建立了交叉口静态秩序模型；叠加动态交通流参数后，建立了交叉口动态秩序模型。通过桂林市多个路口的实测数据，对所提方法进行实例验证及参数调整，结果表明了交叉口秩序的影响因素与变化规律，为交叉口交通拥堵产生率提出量化指标，并为交叉口参数与交通拥堵产生率的定量研究奠定基础。

交叉口复杂度；交叉冲突点；交叉口秩序；交通拥堵产生率

0 引 言

目前交叉口秩序水平的评价标准往往等同于交叉口的服务水平，然而实际状况中，产生拥堵的交叉口与服务水平并无直接量化关系，表明不能简单依据交叉口服务水平客观界定交叉口的秩序程度。随着城市化进程的加快，道路交叉口数量的急剧增长，如何较为全面结合交叉口信息，建立合理评价交叉口秩序状况的模型，以提高交叉口交通安全，降低交通拥堵产生率迫在眉睫[1-3]。

随着复杂网络理论研究的快速发展，其在城市交通网络中也得到了更为广泛的应用[4]。借助复杂网络理论建立交叉口复杂度模型不仅能够科学客观地反映交叉口运行状态，得出交叉口秩序的量化值，也对改善交叉口整体秩序水平、提高交通安全、避免交通堵塞具有重要意义。

交叉口复杂性主要体现于交叉口的冲突点种类及其数量，而交通流在交叉口的分流、合流、交叉是产生交叉口拥堵的根本原因。着眼于此，前苏联学者费舍里松基于冲突点的数量提出了如下的交叉口复杂度模型[5]：

C=No+3Nc+5Nj，

(1)

式(1)中：C为交叉口复杂度；No、Nc、Nj分别为车流的分流冲突点、合流冲突点和交叉冲突点数量。模型(1)仅反映了静态条件下交叉口冲突类型与交叉口复杂度的关系，但实际情况下，不同交叉口由于车道配置、信号相位的不同，静态复杂度并不相同，因此，为评价交叉口资源配置对交叉口秩序的潜在影响，有必要完善并提出交叉口静态秩序模型；对于同一交叉口而言，在不同流量条件下，其运行状态也会有较大的差别，为评估交通流对交叉口运行所造成的秩序影响程度，可建立交叉口动态秩序模型。

1 交叉口静态秩序模型

1.1 交叉口静态秩序模型定义

依据以上分析，交叉口静态秩序模型可定义：由交叉口进口道车道配置、信号配时等固定参数决定，在无交通流输入条件下，用以反映交叉口交通拥堵产生率的静态模型。

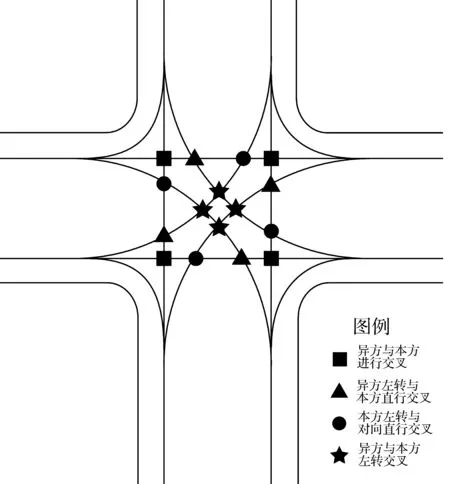
图1 无信号条件下四路交叉口交叉冲突点分析Fig.1 Conflict point analysis of the four way intersection with no signal

1.2 交叉口静态秩序模型建立

在交叉口分流、合流、交叉冲突点基础上，基于模型(1)的条件下，引入交叉口车道配置和信号配时参数，研究在四路交叉条件下交叉口冲突点规律[6-7]，从而建立基于交叉口复杂度的交叉口静态秩序模型。

车道配置影响着交叉冲突点数的数量，在无信号条件下，交叉口合流、分流冲突点仅与交叉道路数量有关，其中合流、分流冲突点仅与交叉口相交道路条数有关，较为单一；交叉冲突点数由异方与本方直行车流、异方向左转车流与本方直行车流、本方左转车流与本方对向直行车流、异方与本方左转车流交叉产生[8-10]，较为复杂。鉴于交叉口类型主要以四路交叉为主，本文从实际出发，暂不对五路交叉以上的复杂交叉口研究。

1.2.1 无信号条件下(以四路交叉口为主)交叉口静态秩序模型

依据本文分类，分析交叉冲突点如图1所示。

①异方与本方直行车流交叉点数

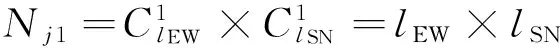
(2)

式中：Nj1为异方与本方直行车流交叉点个数；lEW为东西方向直行车道数；lSN为南北方向直行车道数。

②异方向左转车流与本方直行车流交叉点数

任一方向交叉点数为异方向左转车流左侧方向进口道直行车道数，可推出异方向左转车流与本方直行车流交叉点个数Nj2为：

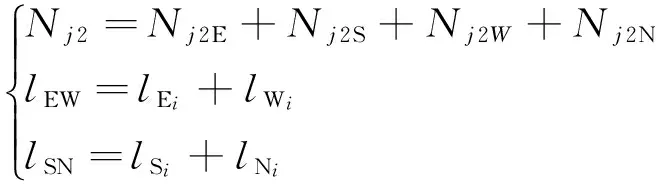
(3)

式中：Nj2为异方向左转车流与本方直行车流交叉点个数；lSi、lWi、lNi、lEi分别表示南、西、北、东方向直行车道数。

③本方左转车流与本方对向直行车流交叉点数

任一方向交叉点数为本方对向进口道直行车道数，可推出本方左转车流与本方对向直行车流交叉点个数Nj3为：

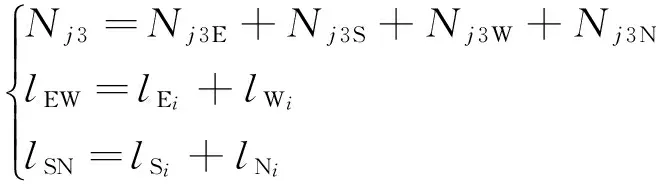
(4)

式中：Nj3为本方左转车流与本方对向直行车流交叉点个数。

④异方与本方左转车流交叉点数。

左转车流两两相交，形成了复杂网络理论中的完全规则网络——具有平移对称性的网络，任何格点的近邻数目都应相同。因此，异方与本方左转车流交叉点个数为：

Nj4=nr，

(5)

式中：Nj4为异方与本方左转车流交叉点个数；nr为相交道路条数。

由于Nj=Nj1+Nj2+Nj3+Nj4，且合流与分流冲突点仅与交叉道路数nr有关，可建立无信号条件下交叉口静态秩序模型如下：

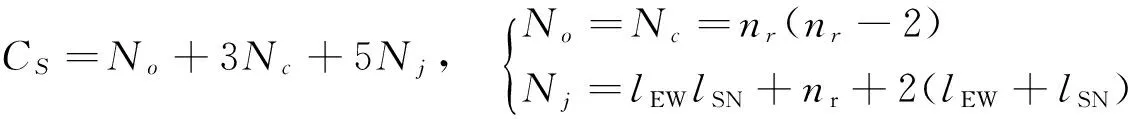
(6)

式中：CS为交叉口静态秩序值。由此，可通过相交道路直行车道数唯一确定交叉口静态秩序值。

1.2.2 信号条件下(以四路交叉口为主)交叉口静态秩序模型

在信号条件下，由于交通流的运行受到了严格制约，其冲突点个数也随相位放行方式而改变[11-13]，因此，在基于上节模型的基础上，需依据不同相位下交通流的放行方式而决定冲突类型和数量，并按一定比例加权得信号条件下的交叉口静态秩序模型。

分析每相位左转与冲突点的特征，建立信号条件下交叉口秩序模型如下：

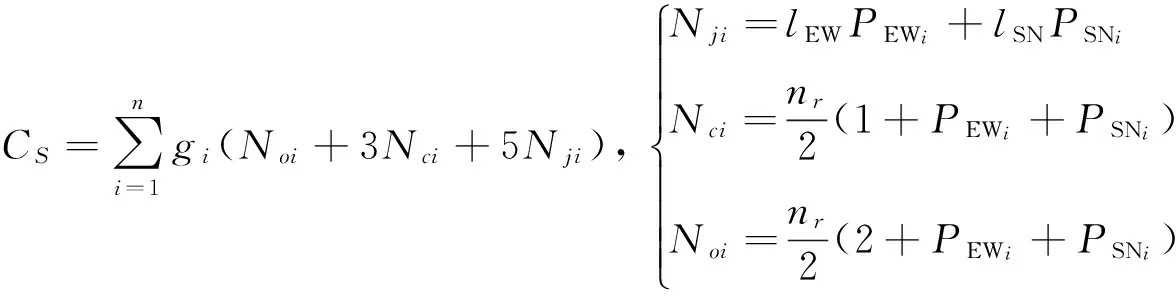
(7)

式中：gi为第i相位绿信比；Nji、Nci、Noi分别表示第i相位交叉、合流、分流冲突点数。

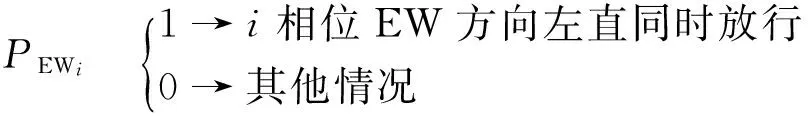
2 交叉口动态秩序模型

2.1 交叉口流量归一化

在交叉口车道配置，信号相位既定的前提下，影响交叉口动态秩序的因素为交通流(按车种将实际量标准化)，其中最突出的即为机动车与非机动车流量。而一般情况下，道路交通流以机动车为主，因此，本文借鉴吕晨曦等[14]关于电动自行车对交叉口通行能力的影响研究，依据直行非机动车令直行通行能力折减比例公式：

Ys2=2 157-0.571x6，

(8)

其中：Ys2为直行机动车饱和流率(辆/小时/车道)，x6为电动自行车流率(辆/小时)，折入直行机动车流量，则可得直行糅合流量公式为：

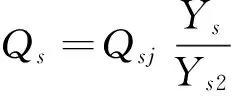
(9)

式中：Qs为直行糅合流量；Qsj为机动车直行流量；Ys为机动车最大饱和流率，即为2 157(辆/小时/车道)，则总流量Qt的计算公式为：

豆禾2∶1混播显著降低了禾草的SOD和POD活性，禾草受种间竞争胁迫影响较大。2∶2混播时，禾草和苜蓿均具有较高的SOD和POD活性，禾草生长良好，受种间竞争胁迫伤害相对较小。

(10)

式中：Qli、Qsi、Qri分别表示第i个进口道左、直、右转糅合流量。

2.2 交叉口动态秩序模型建立

2.2.1 无信号条件下(以四路交叉口为主)

在无信号条件下交叉口静态秩序模型的基础上，根据各冲突类型中，各转向流量占总流量的比值公式为：

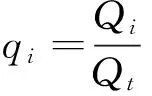
(11)

式中：qi为i的车流占总车流的比值，i代表某方向或某转向。由于处于交通流影响下，在相同车道配置、信号控制条件下，其交叉口动态秩序值即反映了交通拥堵产生率，显然与总流量呈正相关关系，另一方面，交通拥堵产生率也与冲突点类型及数量有关。因此，可假定无信号条件下交叉口动态秩序值为：

CD=Qt(No+3Nc+5Nj)。

(12)

对于合流冲突点Nc与分流冲突点No，由式(6)可知无信号条件下分流与合流机会均等，因此叠加流量后可将左转与直行的冲突点及直行与右转的冲突点等价计入模型。

对于交叉冲突点Nj，需按交叉冲突点产生类型，即异方与本方直行车流、异方左转车流与本方直行车流、本方左转车流与本方对向直行车流、异方与本方左转车流分析。

基于式(6)，异方与本方直行车流动态秩序值Nja为：

Nja=lEWlSN×qEWs×qSNs。

(13)

异方左转车流与本方直行车流动态秩序值Njb、本方左转车流与本方对向直行车流动态秩序值Njc分析如表1所示：

表1 交叉冲突点动态秩序值分析

由表1分析可得：

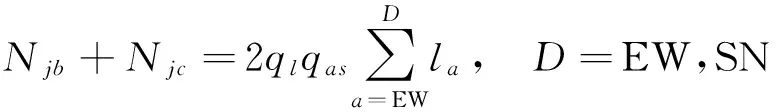
(14)

异方与本方左转车流动态秩序值Njd为：

Njd=nrqEWlqSNl。

(15)

由此确定无信号条件下交叉口动态秩序模型如下：

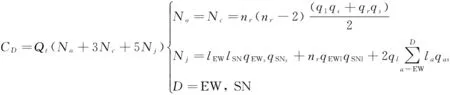
(16)

2.2.2 信号条件下(以四路交叉口为主)

本文“1.2.2”已从不同相位下左转的交叉冲突点出发，归纳了静态秩序模型，而动态条件下需结合不同相位放行方式，叠加交通流数据，从而建立科学合理的动态秩序模型。因此有必要研究不同相位下，冲突点与参与交叉流量的关系。

目前主流相位配置以提高交叉口通行能力为目标，一般采用对称形式，主要为两相位、三相位、四相位，其相位图如表2所示：

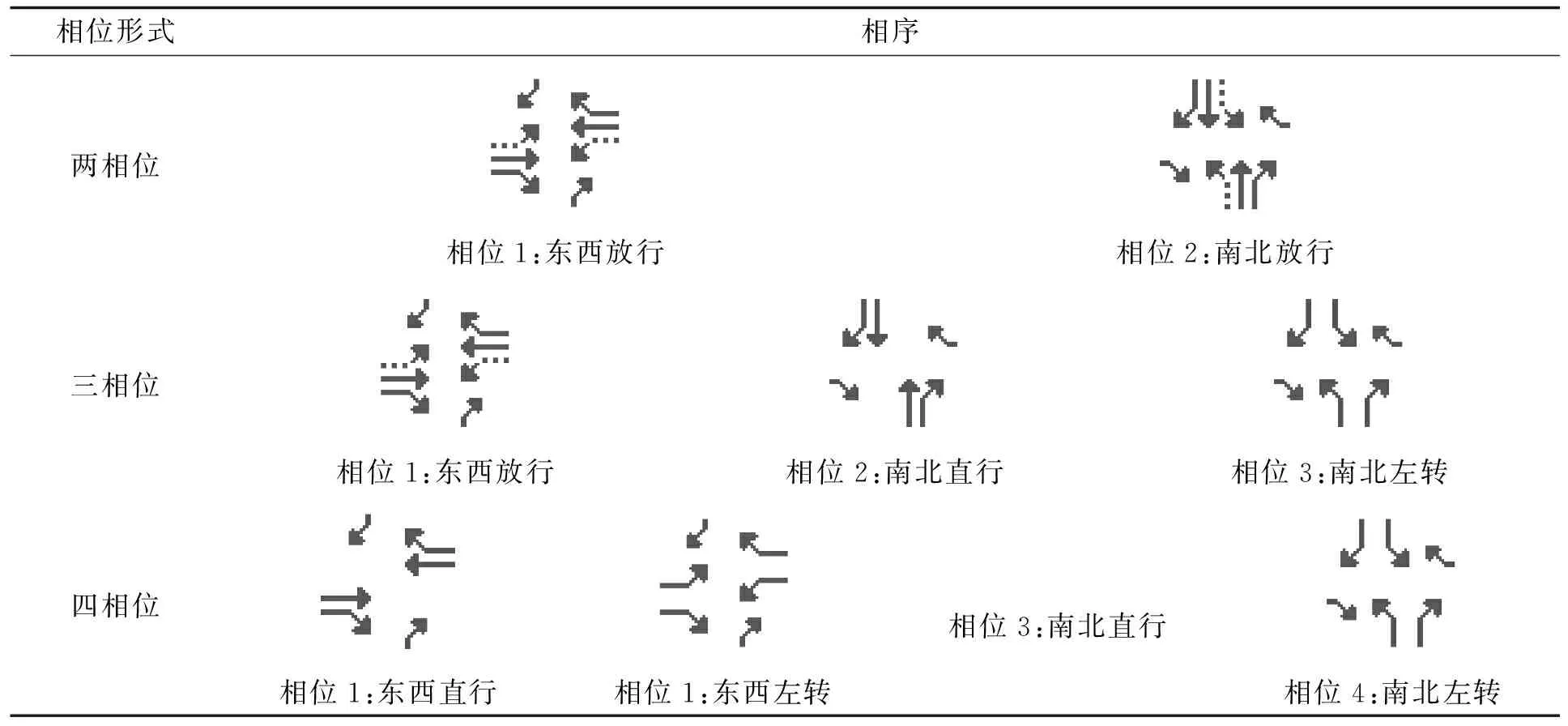
表2 主流相位配置

对信号条件下交叉口合流、分流、交叉冲突点分析如下：

①交叉冲突点Nji

按信号条件下表2的放行方式分析，交叉冲突形式仅为本方左转车流与本方对向直行车流，按不同方向可计算得：

Nji=lEWPEWiqEWlqEWs+lSNPSNiqSNlqSNs。

(17)

②合流冲突点Nci

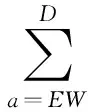
③分流冲突点Noi

由于右转车辆放行不受限制，则在全周期内均有直右分流冲突；若设有左转专用信号，则相应有左转专用车道，直左分流冲突在进入交叉口前即已完成，即直左分流冲突取决于是否有专用左转相位。

由以上分析，可建立信号条件下交叉口动态秩序模型如下：

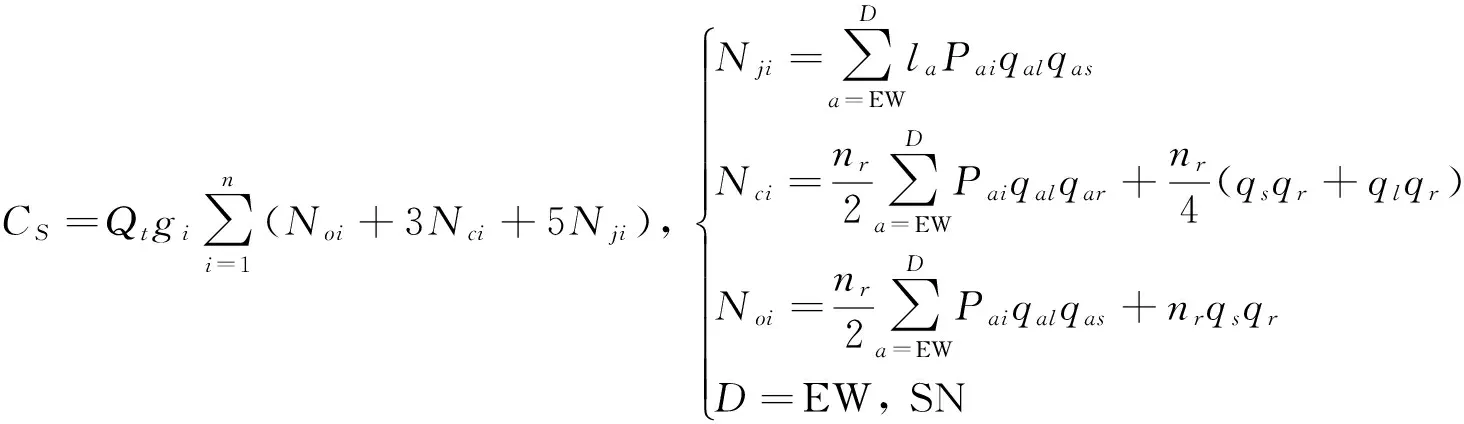
(18)

3 算 例

借助桂林市东二环路与六合路交叉口的实测数据，计算该交叉口静态、动态秩序。东二环路与六合路交叉口东接高速出口，为桂林市最主要的交通节点，日交通量较大。相交道路均为城市主干道，东二环路为双向六车道，六合路为双向四车道，其交叉口主要交通参数见图2～图5。

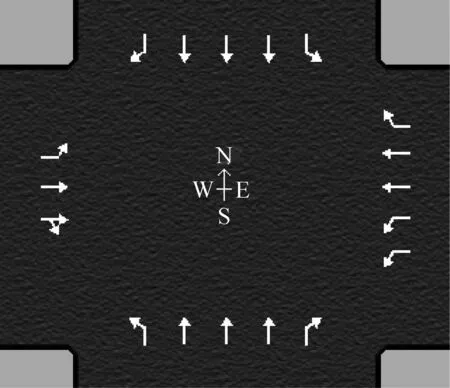
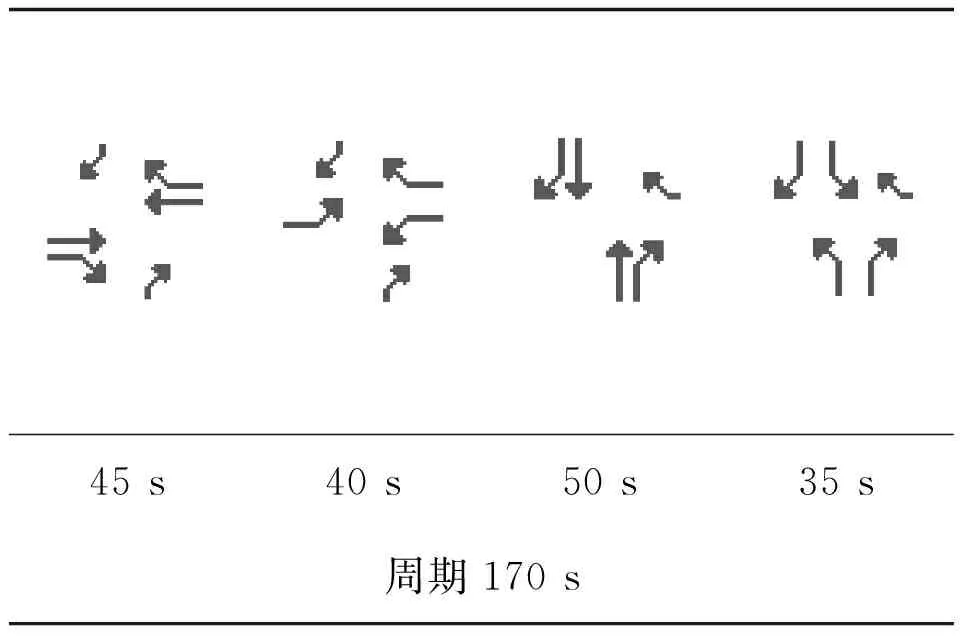
图2 进口道车道配置

图3 现状信号控制

Fig.3 Status signal control

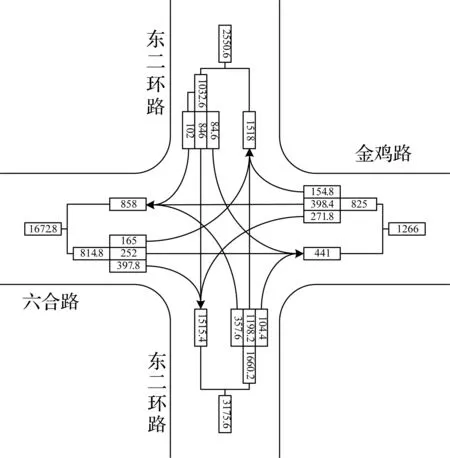
图4 早高峰机动车流量

Fig.4 Morning peak motor vehicle flow

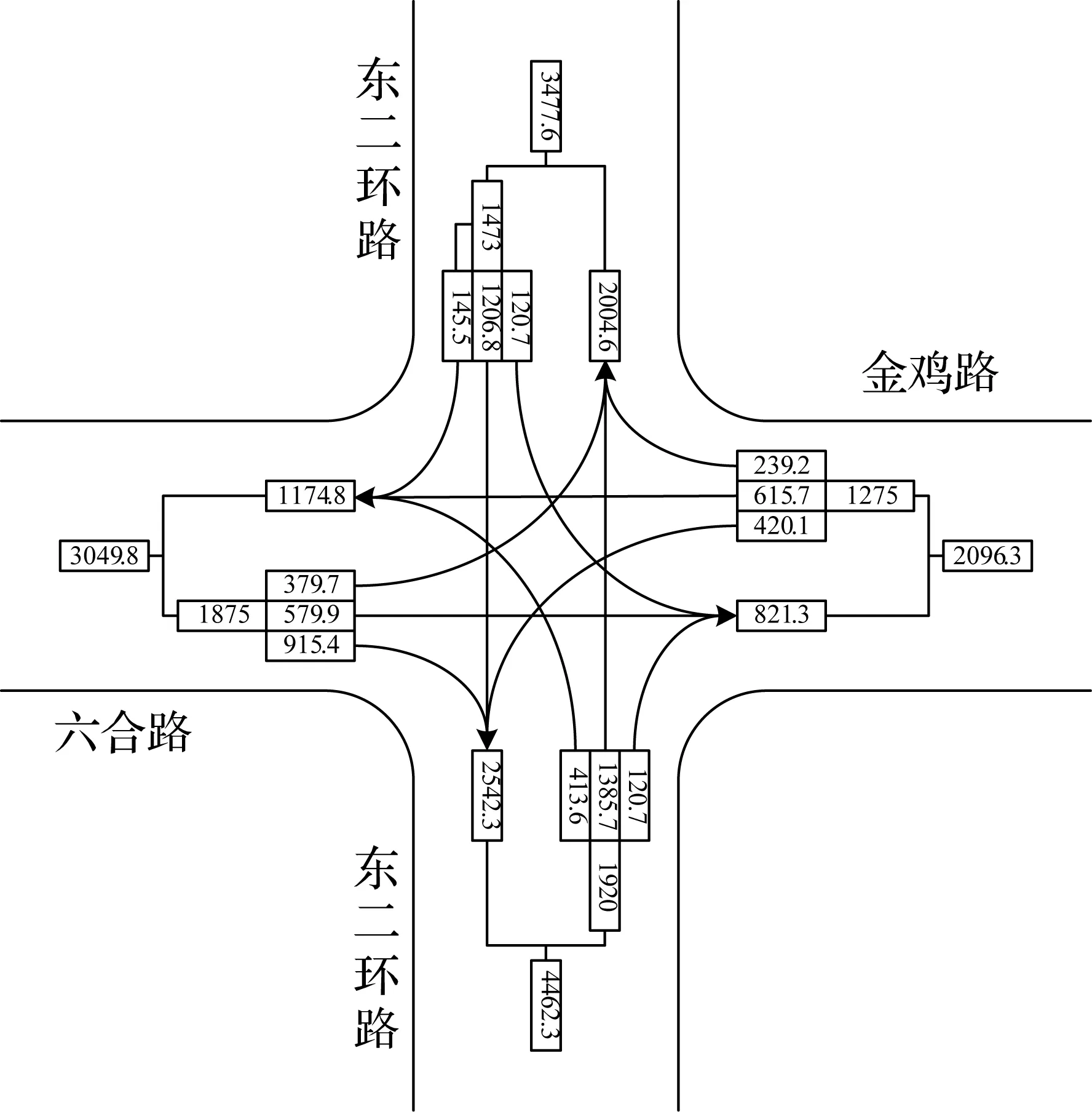
图5 早高峰非机动车流量

Fig.5 Morning peak non motor vehicle flow

依据信号条件下动静态交叉口秩序模型，运用Matlab计算结果得东二环路—六合路交叉口静态秩序为CS=10，动态秩序为CD=4 105。

若分别改变其车道配置、信号相位、流量大小，可得如下动、静态秩序值：

表3 改变条件后动静态秩序值

采集桂林市50多个不同类型四路交叉口数据，并进行秩序运算，改变多种变量测试后表明，交叉口秩序有以下规律：

①在不影响进口道分流的情况下，且交叉口内因信号控制不存在冲突点时，改变车道数并不影响交叉口动静态秩序；

②在相同车道配置、交通流状态下，采用专用左转相位可较大程度提高交叉口秩序水平；

③机动车流量与交叉口动态秩序成正相关，但影响系数不高。

4 结 语

结论与成果：

①基于交叉口复杂度概念，从合流、分流、交叉冲突点入手，结合车道配置、信号相位、交通流等参数建立了交叉口秩序模型，用以表示交叉口的运行秩序优劣状况，表征交通拥堵产生率；

②示例计算了交叉口的动静态秩序值，并通过大量实例，证明交叉口秩序与车道配置、信号相位、交通流的定性关系。

研究不足与展望：

①交叉口秩序与各交通参数间的定量关系不太确定；

②需研究交叉口秩序数值与交叉口拥堵产生率的关系，从而规定交叉口的秩序等级;

③需进一步研究交叉口服务水平与秩序之间的关系，用以定量确定交叉口效率。

[1] GAN X B,WANG Y,LI S H,et al.Vehicle routing problem with time windows and simultaneous delivery and pick-up service based on MCPSO[J]. Mathematical Problems in Engineering,2012(2)：603-621.

[2] XIE Y S,SHEN G J,CHEN X.Fuzzy neural network control technique and its application in a complex intersection[J]. Energy Procedia,2012,16:1408-1415.

[3] MICHAEL B, ANUSCH T, MICHAEL U.Coloring random intersection graphs and complex networks[J]. SIAM J Discrete Math, 2009,23(1):288-299.

[4] 吴建军,高自友,孙会君,等.城市交通系统复杂性—复杂网络方法及其应用[M]. 北京：科学出版社,2010.

[5] 费舍里松 M C.城市交通[M]. 北京:中国建筑工业出版社,1984.

[6] 刘飞.城市道路平面交叉口复杂度计量模型研究[D]. 南京：东南大学,2008.

[7] 沈家军,王炜.基于交通流动态特性的交叉口复杂度模型研究[J]. 土木工程学报,2011,44(5):131-135.

[8] 袁晶矜,袁振洲.信号交叉口通行能力计算方法的比较分析[J]. 公路交通技术,2006(5):123-128+132.

[9] 陈啸,王正.交通影响评价中交叉口服务水平综合评价研究[J]. 现代交通技术,2012,9(2):80-84.

[10]林丽.无控交叉口冲突点延误分析[J]. 南京林业大学学报,1999，23(1):83-85.

[11]刘广萍,裴玉龙.信号控制下交叉口延误计算方法研究[J]. 中国公路学报,2005，18(1):108-112.

[12]赵雨旸,曹立志,迟秋玲,等.信号交叉口HCM2000法延误计算修正模型研究[J]. 黑龙江工程学院学报,2015，29(1):1-4.

[13]张惠玲,王益,尹宝计,等.基于实时延误的交叉口控制方案优化分析[J]. 广西大学学报(自然科学版),2015，40(1):149-154.

[14]余子威,姚海星,许文俊,等.电动自行车对交叉口通行能力的影响研究[J]. 宁波工程学院学报,2014,26(4):28-33.

(责任编辑 唐汉民 梁碧芬)

An intersection order model based on intersection complexity

LI Wen-yong1， YU Zi-wei1， WANG Tao1， HE Jun-jie1， LI Jia-jie2

(1.School of Architecture and Transportation Engineering, Guilin University of Electronic Technology, Guilin 541004, China；2.School of Traffic and Transportation, Beijing Jiaotong University，Beijing 100044, China)

Nowadays, the present intersection evaluation indexes which are only evaluated by service level of intersection can not reflect the level of intersection order accurately. Based on intersection complexity model, the paper analyzes the numerical relationship of vehicle merge, split and conflict points of intersection under the condition of different lane configuration and traffic signal timings. Then a static order model of intersection is established, as well as a dynamic order model is established after superposing dynamic traffic flow parameters. Based on the measured data of multiple intersections in GuiLin, the presented method is valdated by some examples with adjusting parameters. The results show the factors and changing rules of intersection order. It provides the quantitative index for the generation rate of intersection traffic jam, and lays the foundation for quantitative analysis of intersection parameters and generation rate of intersection traffic jam.

intersection complexity; cross conflict points; intersection order; generation rate of traffic jam

2016-01-24；

2016-03-08

国家自然科学基金资助项目(51268006；51408145)；广西自然科学基金资助项目(2014GXNSFBA118255)

李文勇(1976—)，男，河南南阳人，桂林电子科技大学教授，博士;E-mail：3203354931@qq.com。

李文勇,余子威,王涛,等.基于交叉口复杂度的交叉口秩序模型[J].广西大学学报(自然科学版)，2016，41(5)：1538-1544.

10.13624/j.cnki.issn.1001-7445.2016.1538

U491

A

1001-7445(2016)05-1538-07