一类Kukles型多项式微分系统的极限环

乔建元，水树良

（浙江师范大学 数理与信息工程学院，浙江 金华 321004）

［数理科学与信息科学研究］

一类Kukles型多项式微分系统的极限环

乔建元，水树良

（浙江师范大学 数理与信息工程学院，浙江 金华 321004）

考虑一类以圆为不变曲线的Kukles型多项式微分系统。运用一阶、二阶和三阶平均理论，得到了这类系统存在从线性中心分支出极限环最多个数的一个上界。

极限环；Kukles系统；平均理论

实平面微分方程定性理论的一个主要问题是判定极限环的存在性、唯一性、个数和稳定性。对于一般的多项式系统，这些都是非常困难的问题。本文考虑下面的所谓Kukles多项式微分系统：

其中qi，i∈R和A1＞0。当n1∈｛2k，2k-1｝时，得到了从线性中心分支出至多k-2个极限环的结论。运用平均理论，文献［10-11］讨论了较一般的Kukles多项式微分系统极限环的个数问题。本文将讨论一类一般的Kukles多项式系统，运用平均理论得到了共存于不变曲线极限环的最多个数的一个上界。

1　预备知识

为了得到周期轨的存在性，本文用到了一阶、二阶和三阶平均理论［12-13］。该法为非自治周期系统和自治平均系统建立起定量的联系。考虑微分系统：

其中Fj:R×D→R和R:R×D×（-ε0，ε0）→R是连续函数，并且它们的第一个变量是T周期的，D∈R是一个开集。

假设如下的两个假设1和2成立。

假设1Fj（θ，·）∈C3-j。

其中 j=1，2，3，θ∈R，Fj，R，关于第二个变量满足局部利普希茨条件，R关于ε是二阶可微的。定义Fk，0:D→R，其中k=1，2，3。

假设2V⊂D是一个有界的开集，对于每一个ε∈（-ε0，ε0），存在aε，3∈V，使得F1，0（aε，3）+εF2，0（aε，3）+ε2F3，0（aε，3）和dB（F1，0+εF2，0+ε2F3，0，V，aε，3）≠0。那么对于充分小的ε＞0，存在一个T周期解φ（·，aε）使得当ε→0时φ（0，aε）→aε，3。表达式dB（F1，0+εF2，0+ε2F3，0，V，aε，3）≠0的意思是函数F1，0+εF2，0+ε2F3，0:V→R在点 aε，3处的Brouwer度不等于0。使得这个不等式成立的一个充分条件是函数F1，0+εF2，0+ε2F3，0在点aε，3处的雅可比行列式不等于0。

引理1如果F1，0不恒等于0，那么F1，0+εF2，0+ε2F3，0的零点主要是F1，0的零点，这叫作一阶平均理论。

引理2如果F1，0恒等于0和F2，0不恒等于0，那么 F1，0+εF2，0+ε2F3，0的零点主要是 F2，0的零点，这叫作二阶平均理论。

引理3如果F1，0和F2，0恒等于0而F3，0不恒等于0，那么F1，0+εF2，0+ε2F3，0的零点主要是F3，0的零点，这叫作三阶平均理论。

2　主要结果

考虑以下系统：

其中多项式ql（x，y）的次数是nl-2和ql（0，0）=0，Al＞0，l=1，2，3和R＞0。显然，x2+y2=R2是式（3）的不变曲线，因此要考虑的是其它极限环与x2+y2=R2的共存问题。

定理1假设A2，A3＞0和A1=0，多项式ql（x，y）（ql（0，0）=0）的次数是nl-2。kl≥2和nl∈｛2k，2k-1｝，那么对于充分小的ε，从线性中心x˙=-y，y˙=x分支出来的极限环的最大个数分别是：

3　定理的证明

3.1定理1中（Ⅰ）的证明

证明：多项式

为了计算方便，用到以下公式：

当l=1时，系统（3）可以写为：

将θ当作独立变量，系统（8）变为

其中F1（r，θ）=ε（r2-R2）q1（r，θ）sinθ，

那么

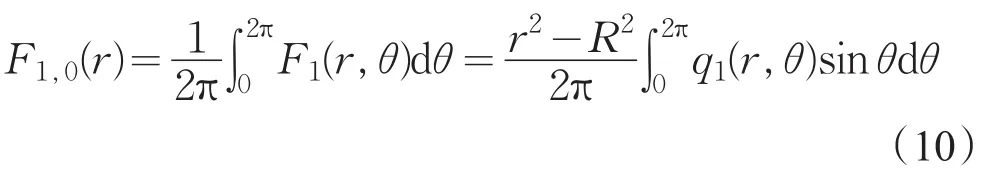
运用式（5），（7）和（10），得到

其中 A=cos2l-2iθsin2iθ，选择合适的多项式系数a2i-1，2l-1使得F1，0（r）有至多k1-1个正根，证毕。

3.2定理1中（Ⅱ）的证明

证明：同理写多项式

用式（6），当l=1，2时，系统（3）变为

式中B=-q1（r，θ）+ε（A2-q2（r，θ）。将θ当作独立变量，系统（13）变为

其中F1（r，θ）=（r2-R2）q1（r，θ）sinθ，

由引理2得F1，0（r）恒等于0。

根据式（11）得到

为了得到表达式

下面给出引理4和引理5。

证明：对式（14）中F1（r，θ）的r求导，得到

再化简式（19）得到

再对r积分并且运用

继续化简式（22）得到

其中D=cos2l-2i+2a-1θsinθ。根据

和式（23），得

证毕。

引理5

证明：根据式（14）推出

根据式（5）、（7）和（12），通过计算得

为了计算

由式（15）和（7），q1（r，θ）可写为

而由式（5）得到

其中（∗∗∗）为式（27），那么根据式（29）、（30）和（31），直接得到引理5，证毕。

根据引理4和引理5，得

其中（∗）（∗∗）为式（18），（∗∗ ∗）为式（27），对式（32）选择合适的系数使得F2，0（r）正根的最大个数是

3.3定理1中（Ⅲ）的证明

证明：多项式

将θ当作独立变量，系统（34）为

根据引理3得F1，0（r）和F2，0（r）恒等于0。由式（11）和（32）可得

为了推导出表达式

下面给出引理6～9。

引理6

证明：由式（20）和（36）得

由式（24）和（36）得

其中aj∈R，m，mj和 nj∈N。由式（5）、（41）和（42）可推出引理6成立，证毕。

引理7

证明：把F2（r，θ）分为两个部分

根据式（12）和（36），得

由式（36）中推出

由式（46）和（47）推出

根据式（5）、（41）和（51），推出引理7成立，证毕。

引理8

由式（36）得Dq2（r，θ）=0，存在j∈R和，j∈N使得

根据式（7）和（21）可得

由式（5）、（54）和（61），可推出引理8成立，证毕。

引理9

由式（5）、（57）和Dq2（r，θ）=0可得

由式（5）和q3（r，θ）知

引理9证毕。

根据引理6～9，最后推出

F3，0（r）=（r2-R2）·

4　结论

通过研究一类一般的Kukles型多项式微分系统，通过对所给多项式的合理变形，运用一阶、二阶和三阶平均理论估计了多项式正根的最多个数，也即得到了共存于不变曲线的极限环最多个数。

［1］KUKLES I S.Sur quelques cas de distinction entre un foyer et un centre［J］.C R.（Doklady）Acad Sci URSS（N S），1944，42：208-211（in French）.

［2］ROUSSEAU C，Schlomiuk D.Thibaudeau P.The centres in the reduced kukles system［J］.Nonlinearity，1995，8（4）：541-569.

［3］CHRISTOPHER C J，Lloyd N G.On the paper of X Jin and D Wang concerning the conditions for a centre in certain cubic systems［J］.Bulletin of the London Mathematical Society，1990，22（1）：5-12.

［4］GRIN A A，Schneider K R.On the construction of a class of generalized Kukles systems having at most one limit cycle［J］. Journal of Mathematical Analysis and Applications，2013，408（2）：484-497.

［5］WU Y B，CHEN G W，YANG X A.Kukles system with two fine foci［J］.Annals of Differential Equations，1990，15（4）：422-437.

［6］LIU Z H，SÁEZ E，SZÁNTÓ I.Limit cycles and invariant parabola in a Kukles system of degree three［J］.Acta Mathematica Scientia，2008，28（4）：865-869.

［7］CHAVARRIGA J，SÁEZ E，SZÁNTÓ I，et al.Coexistence of limit cycles and invariant algebraic curves for a Kukles system［J］.NonlinearAnalysis，2004，59（5）：673-693.

［8］SÁEZ E，SZÁNTÓ I.Coexistence of algebraic and nonalgebraic limit cycles in Kukles systems［J］.Periodica Mathematica Hungarica，2008，56（1）：137-142.

［9］SÁEZ E，SZÁNTÓ I.Bifurcations of limit cycles in Kukles systems of arbitrary degree with invariant ellipse［J］.Applied Mathematics Letters，2012，25（11）：1695-1700.

［10］LLIBRE J，MEREU A C.Limit cycles for generalized Kukles polynomial differential systems［J］.Nonlinear Analysis Theory Methods andApplications，2011，74（4）：1261-1271.

［11］RABANAL R.On the limit cycles of a class of Kukles type differential systems［J］.Nonlinear Analysis Theory Methods andApplications，2014，95：676-690.

［12］GINÉ J，GRAU M，LLIBRE J.Averaging theory at any order for computing periodic orbits［J］.Physica.Section D：Nonlinear Phenomena，2013，250：58-65.

［13］LI S M，ZHAO Y L，SUN Z H.On the limit cycles of planar polynomial systemwith non-rational first integral via averaging method at any order［J］.Applied Mathematics and Computation，2015，256：876-880.

Limit Cycles for a Class of Kukles Polynomial Differential Systems

QIAO Jianyuan，SHUI Shuliang
（College of Mathematics Physics and Information Engineering，Zhejiang Normal University，Jinhua 321004，Zhejiang，China）

In this paper，we consider a class of Kukles polynomial differential systems，the invariant curve of which is circle，and obtain the upper bound of the maximum number of limit cycles that bifurcate from the period orbits of linear center using the averaging theory of first，second and third order.

limit cycle；Kukles system；averaging theory

O175.25

A

1672-2914（2016）02-0037-08

2015-10-10

国家自然科学基金项目（11172269，11171309）；浙江省自然科学基金项目（Y6110195）。

乔建元（1989—），男，山西朔州市人，浙江师范大学数理与信息工程学院硕士研究生，研究方向为微分方程与动力系统。

水树良，副教授，E-mail：shuisl@zjnu.cn。