艾萨克·巴罗英文版《欧几里得原本》分析

陈梦鸽，萨日娜

（上海交通大学 科学史与科学文化研究院，上海 200240）

艾萨克·巴罗英文版《欧几里得原本》分析

陈梦鸽，萨日娜

（上海交通大学 科学史与科学文化研究院，上海 200240）

讨论巴罗拉丁文版和英译本《欧几里得原本》的底本问题，重点研究英译版本，明确其具体出处、编写目的和原因等。主要以巴罗英文版的第一卷为例，详细分析其中的定义、假定、公理、命题，考察其主要表述方式和编写特点。研究表明，巴罗在证明过程中的符号化特征明显，简洁有力的表达方式，走在同时代数学家的前列。

艾萨克·巴罗；《欧几里得原本》；英译本；第一卷

艾萨克·牛顿曾说：“如果我看得更远，是因为我站在巨人的肩膀上。”牛顿是科技历史长河中的巨人，他背后的巨人之一便是他的导师艾萨克·巴罗（Isaac Barrow，1630—1677）。巴罗是多才多艺的学者，精通希腊语、拉丁语、意大利语、法语等多种语言。他是数学家、神学家、语言学家，也是著名的教育家，又作为剑桥大学第一任卢卡斯教授，三一学院院长而负有盛名。他被评价为人谦和，曾长期致力于学校教育。巴罗一生著作丰厚，在数学方面主要翻译《欧几里得原本》①Euclid’s Elements在中国一般译为《几何原本》，这一名词是来自徐光启所译。笔者认为《几何原本》只能代表Euclid’s Elements的中译本。而本文所研究巴罗英译本Euclid’s Elements:The Whole Fifteen Books Compendiously Demonstrated如果直接译成《几何原本》不妥，这里涉及作者不同，语种不同。因此，本文中笔者都作如上翻译。（Euclid’s Elements）、《已知数》（Euclid’s Data），并撰写《光学现象讲义》（Lectiones Opticorum Phenomenon）、《光学和几何学讲义》（Lectiones Optic et Geometric）、《数学讲义》（Lectiones Mathematic）等著作。

巴罗以Piérre Hérigone翻译的《欧几里得几何学原本》②在巴罗英译本前言中，巴罗将其名字写为“Peter Herigon”，应为Piérre Hérigone的英译名。所根据的版本应是Hérigone所著Cursus Mathematicus中第一卷关于欧式几何学的内容。Hérigone版本为拉丁语和法语对照。本文均用其法语名。为底本，于1655年出版自己翻译的《欧几里得原本》（Euclid’s Elements:The Whole Fifteen Books Compendiously Demonstrated）的拉丁语译本；1660年巴罗在自己翻译的拉丁文本基础上出版了英语译本，是《欧几里得原本》各版本中数学符号化的代表之作。巴罗英译本《欧几里得原本》在英国作为标准的几何学教材长达半世纪之久。很多人对巴罗《欧几里得原本》的教育价值也作出了极高的评价。例如，John More爵士认为所有Christ’s Hospital的数学学院男生都应学习巴罗的《欧几里得原本》［1］43。在该书出版半个世纪后，John Keill也给予了很高的评价：“（他）保留了欧几里得的建构和证明……他的建构更清晰明了，更简单地呈现出古代几何学家复杂的思想。为了达到这一目的，巴罗增加了一些推论和评注，简化了后面的一些证明。”［1］43

本文拟以巴罗英译本《欧几里得原本》第一卷为例，详细分析其中的定义、假定、公理、命题、定义、问题等特点。

1　巴罗英文版《欧几里得原本》的底本、编写目的

据巴罗拉丁文版《欧几里得原本》扉页所写，1655年出版的拉丁语版是献给三位当时在校学生：Edward Cecil，John Knatchbull和Francis Willughby①参见Isaac Barrow1655年Euclid’s Elementorum Libri XV Breviter Demonstrati扉页。。巴罗当时已经在剑桥任教，书籍扉页上写着献给当时在校生，有些令人惊奇。不过这也从侧面说明巴罗致力于教育，对学生无私奉献的品质。两年后（1657年），出版商将巴罗编写的欧氏《已知数》与其《欧几里得原本》一同出版，此后这两本册子都在一起出版。本篇文章所讨论的版本是1660年出版的巴罗英文版《欧几里得原本》。巴罗版《欧几里得原本》借鉴了法国学者André Tacquet编写的八卷本《平面几何与立体几何原论》（Elementa Geometriae Planae et Solidae）中的一些内容，沿用了法国数学家Piérre Hérigone所编写的欧式几何学中的体例、命题顺序等［2］序言。这里会产生一个问题：在巴罗之前，拉丁语、希腊语各类版本的欧式几何学比比皆是，如克拉维乌斯（Clavieus）1574年第一版发行的欧式几何学曾被T L Heath评价为“非常有用的著作”［3］105，康曼迪诺（Comandinus）1572年版也被T L Heath认为是“最重要的拉丁语译本”［3］104。为什么熟知拉丁语的巴罗没有进行现在所谓的“大众化”的选择而是采用了比较“小众”②此处笔者对“大众”和“小众”的区分主要根据Heath版Euclid’s Elements前言部分对各版本的评价。对于巴罗所采用的两个版本，Heath评论极少；但对克拉维乌斯以及康曼迪诺本则有很详细的分析。很多西方版本也均是根据这两个版本编译。的版本呢？解答这一问题，要了解巴罗编写欧式几何学的动机和目的以及André Tacquet与Piérre Hérigone两个版本的特点。

首先，André Tacquet的欧式几何学内容（Elementa geometriae planae et solidae）是作为学校里的教科书供教学使用。但只有8卷，并未涉及较难的章节以及数论部分。尽管巴罗很赞赏Tacquet编写的内容，但认为这8卷并不能满足英国一些知识分子的需求［2］序言。所以巴罗编写《欧几里得原本》的动机可能认为Tacquet本过于简略，想对其进行补充，并沿用其中清晰明了的证明方式完整地展现欧氏几何学中的论证技巧和步骤。这正是当时西方发行的各版本欧式几何学中所缺的元素。虽然巴罗之前有完整的15卷本，但都会附有大量的评注和论述；简单明了的版本则内容不全。巴罗的版本涵盖了整个15卷但只有350页，便于阅读携带。这也说明了巴罗版欧式几何学已出版就十分畅销［1］43的原因。

那么，为什么巴罗不重新编纂一本欧氏几何学教科书，而是沿用Piérre Hérigone的体例呢？其一，该书成于巴罗1655年欧洲游学前夕，巴罗没有足够的时间自己重新写一个新的版本。因此选择了Hérigone在其Cursus Mathematica中第一卷欧式几何学的内容作为版本进行改写［2］序言。其二，将数学逻辑证明符号化正契合巴罗的想法。巴罗编写此书的目的是为了“帮助读者的学习”［2］序言，这一点从巴罗欧式几何学拉丁语版的扉页中可以了解。这是献给三位在校年轻学生的一本著作，因此内容简洁易懂是他撰写的目标之一。而符号化则是有力的工具。同时，巴罗对前人的版本也不是特别满意。他认为前人版本中纯语言叙述使命题累赘繁复，命题之间的相互关系不明了。证明中诸如连词和形容词的缺失也会引起很多误解和难题［2］序言。符号与语言相结合可以解决这一问题。在巴罗那个时代“（目前为止），只有Piérre Hérigone用这种方式（符号化）来阐释欧式几何学。”［2］序言同时，Hérigone在欧式几何学的第一卷命题1后面有大篇幅的关于证明过程三段论的探讨与分析，而在巴罗本中只有关于数学知识的探讨证明。此外，巴罗本中采用的符号大多数来自英国数学家 William Oughtred，因为在当时的英国，Oughtred的符号已被大多数人接受。因此不难看出，巴罗编写的目的就是方便读者学习掌握欧式几何学的知识。正如Hérigone认为，教授数学的最好方法就是将简单明了与易于掌握相结合［4］153-193。

因此可以说巴罗编写《欧几里得原本》时参考的底本主要是由于巴罗自身对书籍的定位，编书目的以及对数学的理解决定的。

2　巴罗英译本《欧几里得原本》第一卷分析

巴罗的英文版《欧几里得原本》只有350页，却涵盖了欧式原本15卷的所有命题①巴罗在前言中叙述到，因为欧几里得是柏拉图学派代表，后两卷关于五个常规立体图形的定理应为欧氏所作，不应省略。，与同类的英文版欧氏几何学著作相比，如比林斯利（H Billingysly）1570年版本（500页左右）、希思（T L Heath）13卷本，可以说内容简洁明了，非常清晰地展现出古人的数学论证方法和技巧。

由于T L Heath版《欧几里得原本》被学者认为是最接近欧几里得原著的版本，也是近代西方各版《欧几里得原本》中比较权威的版本。因此本节将以第一卷为例，以Piérre Hérigone版及T L Heath版为参照，详细分析其中的定义、公理、公设、命题、推论、评注等，揭示巴罗英译本《原本》的特点。

2.1巴罗英译本《欧几里得原本》第一卷概况

巴罗英译本大部分都根据Piérre Hérigone的Cursus Mathematicus一书中第一卷里有关欧式几何学的内容编写。大部分证明方法都是遵照欧几里得原本的做法，但在第2、7、8、9、13卷，巴罗对有些命题进行了改动。他认为一些改动可以让证明更方便简洁［2］序言。

巴罗英译本第一卷共包含36条定义，3条公设，20条公理，以及48条命题。本卷主要研究一些直线图形的相关定理，如三角形、平行四边形等。这些是最基本的图形，因此放在《欧几里得原本》的第一章。命题中运用了归谬、反证、综合等方法讨论3个方面的内容：（1）建构三角形，研究三角形角、边的特殊性质，比较三角形之间的关系；（2）研究有关平行四边形的相关定理，并由平行线的特殊性质得出构造平行四边形的方法，进一步揭示平行四边形的性质；（3）研究三角形与平行四边形的相关性质以及相互关系。

仅第一卷来说，与Piérre Hérigone版比对，笔者发现把巴罗本命题里的证明方法都没有改动，但调整了Hérigone对某些命题评注和推论的顺序，使论证更具有逻辑上的衔接性；删减了一些简单或者关联不密切的评注和推论；拓展和增加了自己的观点和理论，并在有些命题后面增加了对相应定理的应用题。笔者将在下面章节进行详细分析。

2.2巴罗英译本《欧几里得原本》第一卷定义、公理、公设特点分析

2.2.1定义特点分析

首先，巴罗定义虽然数量较多，但所占篇幅很小，省略了大量有关亚里士多德逻辑学上对各个范畴的定义评注。笔者认为这一特点十分有利于读者对数学知识的掌握。无论是比林斯利译本，还是T L Heath译本，或者是以简洁符号著称的Hérigone都包含了有关某些定义的大量评注和补充，如Piérre Hérigone就对点、线等作出详细评述。由此看来，巴罗在编写此书时似乎更注重数学知识的运用而非纯逻辑上的演绎和论述。

其次，除了一些基本定义，如点、线、面，对于其他一些较复杂的延伸概念，巴罗大部分沿用了Piérre Hérigone的体例，在定义后，配图举例及说明。如，在第一卷定义23中，巴罗在文字描述旁：“Of trilateral figures，that is an Equilateral Triangle，which hath three equal sides；such as Triangle A（等边三角形是三边相等的三角形；如三角形A）”附图1。

图1　定义23配图

同时，巴罗在某些定义叙述中也糅合了符号表示，与纯文字叙述相比十分容易理解。如关于垂线的定义10：“When a right line CG Standing upon a right line AB，makes the angles on either side thereof，CGA，CGB，equall one to the other，then both those equall angles are right angles；and the right line CG，which standeth on the other，is termed a Perpendicularto that（AB）whereon it standeth.（当直线CG在直线AB上，使所成相邻角，CGA、CGB相等，则两角为直角；当直线CG在另一直线上时，CG称为这条直线（AB）的垂线）”并配图2。

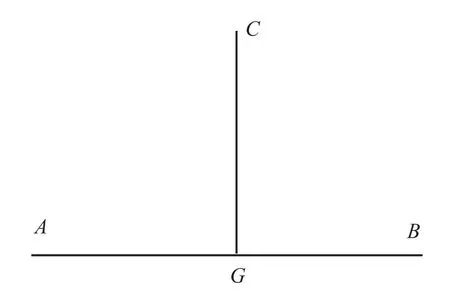
图2　定义10配图

同时，巴罗英译本在下定义时还有一个特点，就是所定义的术语巴罗通常会用两个同义词表示，一般为拉丁语术语与通俗英语表达方式相结合。如定义31：“A rhombus，or diamond figure，is that which hath four equall sides，but is not right-angled.”［2］3再如定 义 33：“All other quadrilateral figures besides these（those that have been mentioned above）are called Trapezia or Tables.”［2］4这种方式至少在Heath版中没有出现过，而Hérigone版本也只出现过一两个。笔者认为，巴罗这种叙述名词的方式十分便于理解，初学者不需耗费大量精力去记住一些专有名词。

最后，笔者拟从内容上谈谈第一卷定义中巴罗自己的特色。第一，在锐角三角形定义之后，即定义28后，巴罗补充了两个相近的概念，即等边或等角图形（equiangular or equilateral figure）及两个图形对应角或边相等。（two figures are equiangular or equilateral）。这一补充在Hérigone版里是没有的，但确实为后面命题的理解扫清了障碍。但为何没有独立成为一条定义呢？在笔者看来，可能是因为此处为巴罗自行添加，但单独成定义与整体又格格不入。定义中还有一处虽为下定义却未单独列出。即关于问题（Problem），定理（Ttheorem），引理（Lemma）以及推论（Corolary）的定义。了解这四者之间的异同能帮助读者更好的了解后面命题的内容和证明过程中的逻辑关系。而同样的，未能像Hérigone一样单独列出定义也可能是因为巴罗编写此书的目的是重在作为一本几何学的教材供大家学习，而非一般逻辑学的书籍。

总而言之，巴罗的定义部分结合了文字叙述，图形示例以及符号表述，通俗易懂地介绍了各种结合学中基本概念，并对一些后面可能出现的模糊概念作出明确。

2.2.2公设和公理特点分析

Heath版本公设（Postulates）和公理（Axioms）各5条；Hérigone版本公设4条，公理20条，且大部分公理仍会延伸出很多小公理，这些小公理是综合之前的公理推导出来的。如：在Hérigone的第12条公理中就包含一条小公理。原公理是：“两个直角相等”［5］29，而延伸的小公理为：“若三只角两两相等，若其中一个为直角，剩下两个都为直角。”［5］30同时，他的每条公理公设都配有图示和符号表述。巴罗版则大体根据Hérigone版本编写，但有些不同，公设只有前三条，公理20条。那么巴罗为什么没有将Hérigone的第四条公设纳入其中，为什么将Proclus的“Commentary on the First Book of Euclid’s Elements”中公设4和公设5列入公理12、公理13呢？可以肯定地说巴罗一定认真研读过Proclus的评论，因为卷一命题2中巴罗提到了有关Proclus的观点。首先要了解一下公理和公设的区别。西方古代学者对公理和公设的却总体来说有3类。

一类是Proclus对公理和公设的区分。Proclus认为公理和公设的区别犹如定理与问题的区分。定理中我们可以提前得到结论，而问题则让我们去找到结论或者去做某项工作。同样地，公理是不证自明的，根据我们的常识很容易理解，阐述某些必要的性质；而公设虽然也很容易理解，不需要复杂的手段，但需要我们找到某个主题（subject-matter），展示一个简单的性质［6］178-179。

第二类认为公设仅用于几何学，而公理对所有研究量和数的学科都有用［6］182。

第三类则是以亚里士多德为代表，认为公理不可证明，且对学习任何事物都十分必要；公设则是可以得到证明的，但无论学习者接受同意与否都要接受的条件。

从这3个观点来看，巴罗英译本只包括三条公设，分别是“过两点作一条直线”，“连续延长有限直线”以及“由任意圆心和半径长度作圆”［2］6。而将“所有直角都相等”以及“同平面内一条直线和另外两条直线相交，若在直线同侧的两个内角之和小于180°，则这两条直线经无限延长后在这一侧一定相交。”［2］7列入公理。由此看来，巴罗更赞同Proclus对公理公设的划分。当然，Hérigone的公设4“给定一个数，可以取比它大的数或更小的数。”［5］51也没有出现在巴罗版的公设和公理中。按照Proclus的标准这显然不在公设之列。

与Hérigone不同，巴罗的公理都是文字表述，基本没有符号语言的转述（除了较复杂的公理13）。这也从侧面证明巴罗认同公理都是一些显而易见，不证自明的定理。另外，巴罗还省略了Hérigone的21条公理，A即不大于B也不小于B则A=B。

2.2.3命题特点分析

巴罗英译本《欧几里得原本》一共有48道命题，其中包括两条延伸定理以及将三个对之前定理实际应用的求作。下面将详细分析巴罗英译本卷一命题的特点。

（1）命题中定理（Theorem）和求作（Problem）的划分。对于欧式几何学中的命题，以思波希波斯（Speusippus）和安菲诺莫斯（Amphinomus）为代表的先哲，将它们全都看作是定理，而另部分以门奈赫莫斯学派为代表的数学家则认为命题都可以看作是求作［3］125。而Proclus认为欧式几何学中的命题有定理和求作之分。他认为定理就是呈现必要的属性；而求作则包括图形的删减则增添，产生或者分割［7］77。Hérigone的Cursus Mathematicus是拉丁语和法语对照。笔者发现，Hérigone在其拉丁语版本中对命题是属于求作还是定理有详细的划分；但在法语版中却没有任何明显划分，统一称作命题（Proposition）。巴罗虽然在命题命名上没有区分定理和求作，但是在每道命题结尾都给出了详细的区分。求作的结论都为：“which/what is to be done.”定理的结论都写作：“which/what is to be Dem.”这就说明巴罗其实很赞同Proclus对命题的区分。而上述两句也正是Proclus对求作和定理区分标准［7］178-179。据此，卷一中的命题属于求作的有14条，属于定理的有34条。巴罗没有采纳Hérigone拉丁语版分开编写求作和定理的体例，笔者认为巴罗可能是担心不同编号混淆层级关系。因为巴罗在某些命题下延伸出自己的求作和定理。并用Problem和Theorem命名。

（2）命题结构特点分析。Proclus认为所有的命题（包括定理和求作）都可以分为6个部分：题述（Enunciation），题例（Setting-out），所求（Definition），构图（Construction），证明（Proof）以及结论（Conclusion）。“题述陈述了已知条件和所要求的解；题例则单独列出已知条件，并加以修改用于后面的证明；求解则清楚明白地陈述所要证明的事物或要求作的事物；构图则是为了求解而需要的图形或已知数；证明是从已知的事实科学推导出一些结论；结论则是对题述的重申。”［7］225

Hérigone版中命题形式完全符合此六分法。只是除了题述为文字表述外，其余5部分全都是由符号化的语言表述。现以命题1为例（如表1）。

由此可见，虽然巴罗声称大部分沿用Hérigone的体例，但在命题表述方面却没有如此清晰地六部分划分，而是将题述、题例和所求3部分用语言和符号糅合在一起。

巴罗这种将图形、符号、语言糅合在一起直接形成一个命题形式，十分简洁有力，省去了过多重复的赘述，又能使读者结合图示立刻理解要求证明的已知量和所求量，十分利于读者学习掌握数学知识。但巴罗对每一题的结论可以说是做到了Proclus所说的结论的两重性，即Proclus认为结论一是题例中具体的结论，二是普遍性的结论，是特殊到普遍的一种过渡。Hérigone版里没有明显体现出这种特殊到普遍的过渡，但巴罗英译本却对此有所强调。再以上述命题1为例，经过证明得出结论三角形ACB为等边三角形，这是题例中的小结论。随后的“which is to be done”则是一种普遍性的结论。

（3）命题内容分析。巴罗命题内容有如下特点：

第一，巴罗不仅在题目叙述上采用符号与语言相结合的简洁方式，其构图，证明的过程也采用此种方式，证明过程也十分简单，多用连词等，形成连贯的思维，便于理解。同时，较之于Heath版本繁琐的语言赘述，和Hérigone全符号表达式的证明过程，巴罗版则处于中间状态，既简洁又保证了思维的连贯性，十分容易理解。

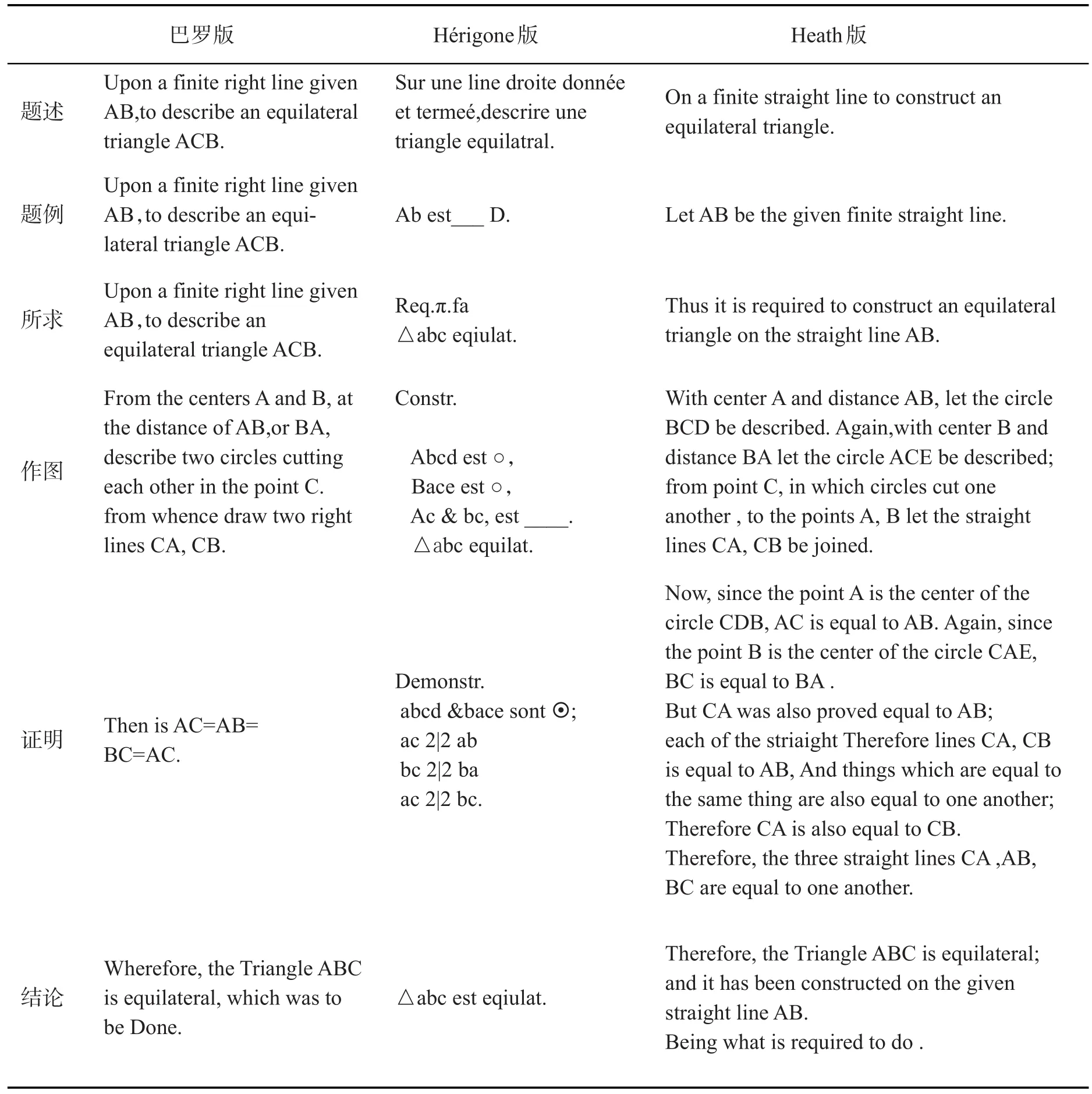
表1　巴罗版、Hérigone版、Heath版命题各部分对比

第二，巴罗英译本《欧几里得原本》可以说只关心数学问题，对于形式逻辑则没有丝毫涉及。如在Hérigone版命题1后有很长篇幅的评注，是Hérigone关于欧式几何证明过程对三段论应用的分析。而巴罗在命题1后的评注则是提及命题1的作图方法也可以做出等腰三角形。相当于利于归约法推及到更广的方面。

第三，巴罗似乎更注重命题内容的深化，注重数学知识的拓展。这一点首先体现在巴罗在命题32后增加了两条延伸定理。定理一是关于多边形内角和，来自与Herigone的评注2，而省略了Hérigone第一条关于多边形边数和所能划分成三角形个数关系的评注。自行增加了定理二，证明所有图形外角和为360°。可能巴罗认为Hérigone原来的评注一有些累赘，而进一步由多边形内角和求得外角和的定理。同时，在命题35后（要求证明两平行线内同底的长方形和平行四边形面积相等），巴罗增加了自己的评注。通过移动和分割的思想得出长方形的面积公式并进一步推出平行四边形的面积公式。这种思想可以说是有一点微积分的雏形。而这一评注也是对原命题的深化，而在命题47（关于毕达哥拉斯定理的证明）后提出3个求作，分别是求平方和线段，平方差线段和直角三角形的斜边。阐释命题应用的方法，很有启发意义。定理或求作不只是单纯的证明，更是要对定理的应用。再如，命题41（关于三角形面积与同底同高的平行四边形面积关系）后，巴罗进一步深化知识，具体推出三角形面积公式。其次，巴罗对Hérigone原有的评注、推论和作图进行取舍，丢弃与命题关联不紧密，或者特别显而易见的论述，取代为自己的一些拓展。如Hérigone在命题9（求作角平分线）和命题10（求作中线）后各附上了用圆规作图的方法，由于二者的作图方式类似，因此巴罗只在命题10后概括地提及到角平分线和中线可以由圆规和直尺作图得到［2］14；却在命题9后面将作图方法推及到4等分，8等分角。

同时，巴罗省略了Hérigone一些与本命题不直接相关的评注，调整了一些评注和推论的顺序，使整个论证逻辑更紧凑严密。如在命题16（三角形任一外角大于相对任一内角）后，Hérigone增加了一条关于直线外一点不可能向该直线作两条相等线段的命题。但与本命题关系并不紧密，巴罗删去。如：命题13（一条直线上的射线与直线形成的两个角之和为180°），Hérigone只有前两条推论即关于命题13中两个角相互关系以及若出现多条射线形成多个角之和。而巴罗的后两条关于两条直线相交形成四个角之和与交于一点的多条射线形成的多个角之和［2］16的推论在Hérigone版是放在命题15之后的。命题15是关于两相交直线对角相等的定理。显然作为推论，巴罗的安排更为合适。再如，Hérigone在命题46（给定线段求作正方形）后附加如下评注：证明定理等边长的正方形面积相等以及面积相等的正方形边长相等［6］54。而巴罗将此作为延伸定理单独列在命题48后，因为在命题48的证明过程中会用到这一延伸定理的结论。

因此，巴罗英译本《欧几里得原本》第一卷，从形式上说，命题内容上更加简洁易懂，更注重数学知识的拓展应用，整个逻辑顺序更加严密。

3　结语

从巴罗英译《欧几里得原本》第一卷可以略窥巴罗本的特点，总结如下：

第一，符号、图形、语言相结合，简洁清楚地展现欧式几何证明的思路，有利于读者对数学知识的掌握和学习。当时传统西方数学惯例基本为纯语言逻辑演绎，不添加任何符号；也有极少数数学家以“符号化”为代表；但巴罗本在命题证明解说过程中，糅合了符号与语言，在当时是不多见的。这种做法更符合现代数学教材的惯例。

第二，注重数学知识的深化而非形式逻辑的探讨，省去了很多关于亚里士多德对于定义、范畴、三段论的解析。没有搜集各类前人的评注，只是增添了某些自己对命题相关知识的拓展，是一部学习初等几何的优秀教材。

总而言之，巴罗的英译本《欧几里得原本》具有极高的教学价值，可以说是当时涵盖命题内容较全面又非常简明的一本几何学教材。

［1］FEINGOLD M.Before Newton：The life and times of Isaac Barrow［M］.Cambridge：Cambridge University Press，1990.

［2］BARROW I.Euclid’s Elements：The whole fifteen books compendiously demonstrated［M］.London，1660.

［3］HEATH T L.The thirteen books of Euclid’s Elements［M］. Cambridge：Cambridge University Press，1908.

［4］ROSA M，ESTEVE M.The role of symbolic language in the transformation of mathematics［J］.Philosophica，2012（87）：153-193.

［5］HAMILTON J.Memoir of isaac barrow［M］//Works of Isaac Barrow.New York:John C.Riker，1845.

［6］HERIGONE P.Cursus mathemticus［M］.Paris：Henry le Gras，639.

［7］MORROW G R.Proclus：A commentary on the first book of Euclid’s Elements［M］.Princeton:Princeton University Press，1970.

［8］莫德.中国人研究《几何原本》的历史意义和存在的问题［C］//莫德，朱恩宽.欧几里得几何原本研究论文集.呼和浩特：内蒙古文化出版社，2006：1-27.

［9］纪志刚.汉译《几何原本》的版本整理与翻译研究［J］.上海交通大学学报（哲学社会科学版），2013，21（3）：27-72.

［10］白尚恕.再论《几何原本之名称》［J］.北京师范大学学报（自然科学版），1993，29（2）：270-275.

［11］HILL A.A life of isaac barrow［M］//Works of Isaac Barrow. New York：John C.Riker，1845.

Isaac Barrow’s Euclid’s Elements（English Version）Analyzed

CHEN Mengge，SARina
（School of History and Culture of Science，Shanghai Jiaotong University，Shanghai 200240，China）

The author discussed the original sources for Isaac Barrow’s Euclid’s Elements（English Version and Latin Version）by clarifying its origins，the motivation of Isaac Barrow and the readers of this book.Then，the paper offered a detailed analysis of the forms and features of the first book through a detailed study of the definitions，postulates，axioms and propositions presented.It can be safely concluded that Barrow’s Euclid’s Elements bears a similar tradition with the modern mathematical textbooks due to its elegant proofs and applications of notations.

Isaac Barrow；Euclid’s Elements；English version；the first volume

N09

A

1672-2914（2016）02-0018-07

2015-11-25

国家社会科学基金项目（13AZS002）；上海市教委创新项目（14ZS0292012）。

陈梦鸽（1990—），女，安徽巢湖市人，上海交通大学科学史与科学文化研究院硕士研究生，研究方向为早期近代西方数学史。

萨日娜，副教授，Email：sarina@sjtu.edu.cn。