基于空间相互作用模型和Markova链的人口流动分析——以江西省抚州市为例

刘军辉张家历

（1.东华理工大学地球科学学院，江西 南昌 330013；2.西南科技大学土木工程与建筑学院，四川 绵阳 621010）

基于空间相互作用模型和Markova链的人口流动分析
——以江西省抚州市为例

刘军辉1张家历2

（1.东华理工大学地球科学学院，江西 南昌 330013；2.西南科技大学土木工程与建筑学院，四川 绵阳 621010）

文章根据地区经济发展水平估算抚州市的合理人口，以此作为空间相互作用模型的到达数量，利用空间相互作用模型计算抚州市人口流动的合理格局，并运用 Markov链预测未来抚州市人口流动的趋势。研究得出，临川区无论是人口流动还是远期的人口占比与抚州市其余县相比均有显著的优势。

空间相互作用模型；Markov链；抚州市

1 引言

根据抚州市人口和产业分布现状，如何分析并预测未来抚州市的人口分布和流向；如果预测存在困难，则退而求其次，如何根据现状资料给出比较合理的人口分配和流动图式。为此，可以采用各区的现实人口作为流动的源人口，即出发人口；然后以各区经济实力水平为权重计算一个合理分布的人口，以此作为汇人口，即到达人口［1］。有了源、汇人口测度，加之区与区之间的交通里程尺度，就可以借助引力模型开展人口流动的动态趋势分析。

在此基础上，将人口流动过程近似视为随机过程，不难运用Markov链［2］的方法预测未来人口分布格局。

2 研究区域概况

抚州市［3］是江西省下辖的地级市，位于江西省东部，地理坐标介于东经115°35′～117°18′，北纬26°29′～28 °30′之间，南北长约222 千米，东西宽约169 千米。抚州市地貌以山地、丘陵为主，全市境内东西南三面环山，中部丘陵与河谷盆地相间，主要有东部的武夷山脉和西南部的雩山。抚州市地处亚热带季风气候，降水量大，水资源丰富，自然资源也很丰富。抚州市东临福建省，南接赣州市，北部与进贤县、余干县毗邻，西连丰城市。抚州市现辖1 区（临川区）10 县（东乡县、金溪县、崇仁县、资溪县、南城县、宜黄县、乐安县、黎川县、南丰县和广昌县）。

图1 研究区域

3 空间相互作用分析

借助空间相互作用模型，研究抚州市人口的空间流动问题。空间相互作用模型有多种形式，最著名的就是Wilson的最大熵模型［4-6］。基于最大熵思想的空间相互作用模型也被视为地理引力模型之一［6-7］，其实它是一种流量的空间分布模型。采用该模型族中的旅行工作模型可以分析并预测一个城市中各个区县之间的人口流动情况。

3.1 空间相互作用模型

假定将一个城镇划分为两类区域：初始区（O）和目的区（D）。初始区也可以叫做源区、出发区，或者叫做发点，目的地也可以叫做汇区、到达区，或者叫做到点。用 Oi表示第 i个初始区的出发量，用Dj表示第j个目的区的到达量，我们需要预测的是各条路上的通行量。于是基于最大熵原理的产生—吸引双重约束引力模型可以表作：

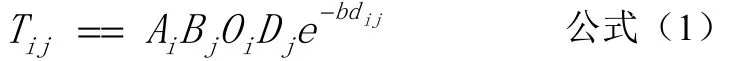
Αi、Bj为2个针对全部出发地Oi和目的地Dj的标度因子的集合，被定义为：

这里序号 i，j=1，2，…，n.标度因子的这种定义形式是为了满足如下约束条件：

上述条件对于所有的Dj和所有的Oi的都能成立，进而保证如下条件成立：

这意味着，所有出发的流等于所有到达的流，等于所有路上的流。式中符号含义如下：Tij为从 i到 j的流动量；dij为从i到j的距离，也可以用流动时间表示；Oi为离开一个地区的人数，即一个地区产生的出发量；Di为根据一个区域吸引的人数估计的工作岗位数目，或者能够接受的人口量。在具体的应用过程中，上述各个公式的符号的含义可以视具体的问题而区别对待。

3.2 数据和分析过程

要开展基于空间相互作用的人口流动分析，我们需要如下数据：出发地的人口，即抚州市各县、区各有多少人口可以出发；到达地的人口，即11个县、区各应该到达多少人口；区与区之间的交通里程或者旅行时间。现在，出发地的人口不成问题，我们不妨采用各县、区总人口为规模测度。虽然一个区域的人口不可能全部出动，但引力分析的有效结果通常也不是绝对的数量，而是相对的比例关系。此外，区与区之间的空间距离也可以借助通常的交通地图估算（表1）。

表1 抚州市辖区的基本数据及其处理结果（2011年）

笔者缺乏的数据在于两个方面：其一，各个区应该到达的人口数量；其二，区与区之间的现实的人口流量。

首先考虑一个合理的人口比例，据此估算各个区理当到达的人口数量。经验表明，人类的行动总是与经济利益有关。经济发达的地区对人群有更大的吸引力，我们假定合理的人口分布与地区生产总值（GDP）成比例。各个区的合理人口规模计算公式如下：

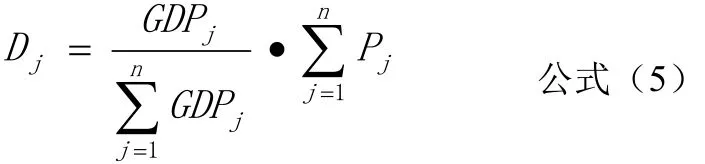
式中：n=11表示区域数；GDPj表示第j个区的地区生产总值（按当年价格计算）；Pj表示第j个地区的人口数量。利用上述公式估算一个合理的人口比例，以此作为到达区人口数量（表1）。区际交通里程可以根据江西省抚州市交通图估算（表2非对角线元素）。至于区内交通里程，经验表明，可以采用下述公式计算：

也就是说，区内交通里程取各个区域面积等效半径的一半长度。将表1中的面积数据代入上式，立即得到区内交通里程的估算数据（表 2对角线元素）。这种定义方式带有一定的主观性，对整个区域人口流动分析有一定影响。不过，笔者关注的是区际人口流动比例。数值模拟实验分析表明，不同的区内里程确定方式对区际人口分配比例的预测影响不大。

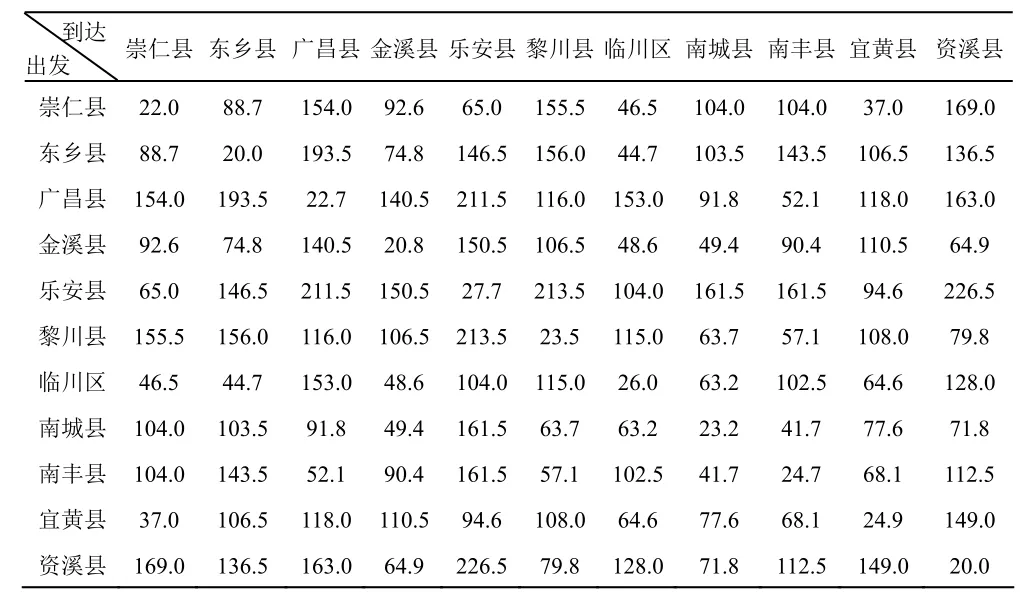
表2 从不同出发区到不同到达区的交通里程（km）

根据表 2中的交通数据，容易计算平均运行距离。在做平均计算时只需要将对角线和对角线以上或者以下的数值加和。简而言之，由于对称性，只需考虑上三角形矩阵或者下三角矩阵。计算结果为：

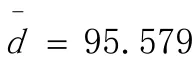
因此，根据经验，距离摩擦系数b值的取值范围应该是：

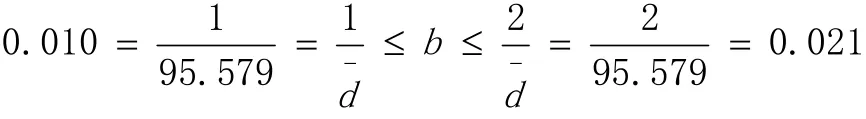
不妨取 0.010和 0.021的中点位置即平均值，于是b=1.5/95.579=0.016。

作为初始值，假定起初区际没有人口交流。这样，各县、区的人口仅仅流入本地；到达人口规模采用基于GDP比例重新分配的人口（表3）。

表3 从不同出发区到不同到达区的初始人口和预期合理人口数

前所述，将人口流动视为产生——吸引双重约束问题，出发人数和到达人数明确，需要预测的是路上的交通流量。这个可以借助空间相互作用的双约模型开展预测分析。首先计算标度因子，麻烦在于两个标度因子相互交织。因此有必要利用迭代法进行参数校验。第一步可设Αi=1（i=1，2…11），运用公式计算Bj值，将Bj值的计算结果代入公式的另一个式子计算Αj值，如此循环往复，直到在一定误差范围内参数值不再变化。在7位小数点以内，计算到第6步的结果与第7步的结果没有分别（表4）。因此，可以在第7步终止迭代过程。但准确起见，不妨往下多迭代几步，本文采用第30步的结果作为标度因子值。有了标度因子值，借助表 3数据，利用Tij的公式，就可以预测理论上的或者合理的区际人流，计算结果列入下表：

表4 标度因子的迭代校准过程（参数0.016）

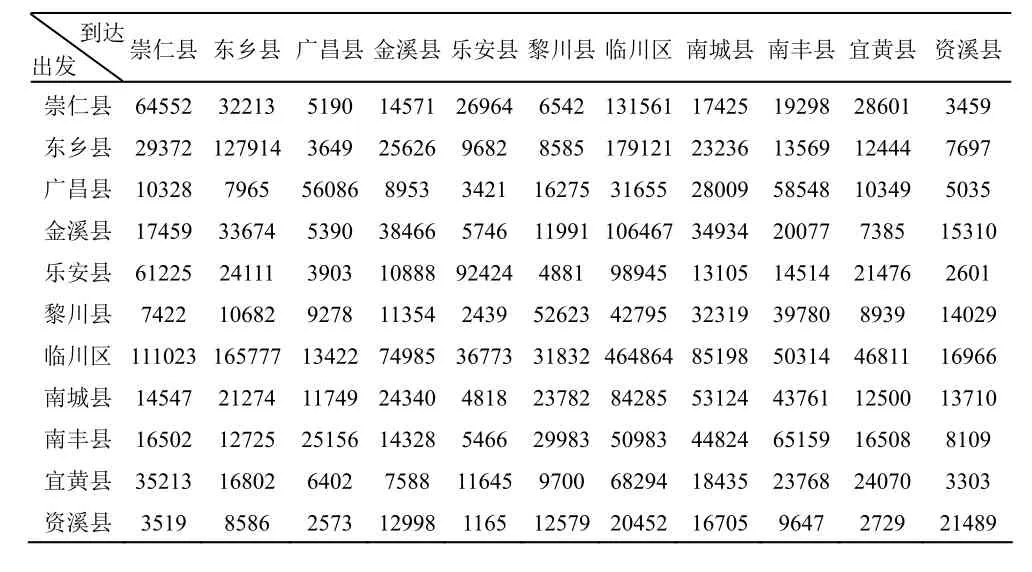
表5 从不同出发区到不同到达区的合理人口

图2 抚州市各县、区流动到各地区的人口占比

3.3 小结

根据上述结果，可以得到如下基本结论。特别强调，由于我们缺乏现实的人口流动数据，下面的分析主要是一种理论上的、基于优化思想的讨论，数据强调的是相对的比例关系，而不是绝对份量。而且，区内流动份量与区际流动份量不具备严格的可比性。不过，区内与区内、区际与区际的份量是可以比较的，正是这方面的结论为未来的城市交通设计提供了可资参考的有用信息。

表6 抚州市人口流动的区内分异

第一，人口流动的区内分异。从表 6可以看出，抚州市10个县的区内流动比例都未超过0.3，而临川区作为抚州市经济政治中心，人口区际外流的动力较小。其区内人口流动比例达 0.42。东乡县虽然距离临川区很近，但由于其自身经济条件也不差，故区内流动比例达到了 0.29；而广昌县虽然经济条件较差，但因为距离临川区很远，其区内人口流动比例还是达到了0.24。

表7 抚州市人口流动的区际差异

第二，人口流动的区际差异。临川区与崇仁县之间的人口流动最为密切，这是因为崇仁县经济状况较差且到临川区的距离近；区际人口流动最弱的是资溪县与乐安县，这主要是因为两地交通不便，即区际可达性差，而且两地经济状况相差不大，故人口流动的动力小。

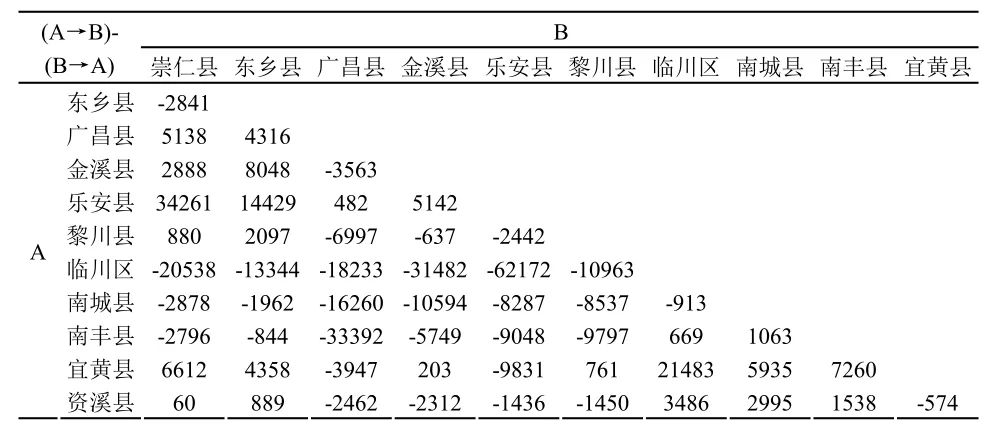
表8 抚州市人口对流的不对称性

第三，人口对流的不对称性。从临川区到乐安县的人口远小于乐安县到临川区的人口，这意味着，相对于临川区，乐安县人口过剩，乐安县应该作为临川区一小部分人口的生活区；此外，从表中容易得出抚州市区际人口更倾向于涌入临川区，而临川区人口则有极小一部分净流入南城县。

4 Markov链分析

Markov链的应用需要一定的前提条件，那就是地理过程为具有无后效性的随机过程。区域和城市的人口迁移一般不具备无后效性质，采用Markov链分析未必合适。但是，在没有更好的预测方法的前提下，可以利用Markov链进行概略的估计。通过上面的引力计算，我们得到一个人口流动的数量分配表（表5）。将表中数据按行加和，计算一个地区流到本区和其他地区的人口比例，就可以得到一个反映区内、区际人口变动倾向的概率转移矩阵（表9）。

表9 区内、区际人口变动的转移概率矩阵（基于空间相互作用）

用表 9初始阶段的概率转移矩阵反复自乘，最后可以得到一种稳定的概率分布，这个分布揭示未来可能的一种人口格局见图3。

图3 抚州市人口远期分配比例

可以看出，未来抚州市一种可能的人口格局是：临川区占33.70%，崇仁县、东乡县和南城县合占31.16%，其余县合占35.14%。这意味着未来抚州市人口会更加紧密的集中在临川区，其人口占比对比2011年上升了5.82个百分点。因此，为了引导人口的合理流向和分布，今后应该进一步加强临川区的基础设施建设和产业发展份量。

5 结论

通过空间相互作用模型和Markov链分析了抚州市的人口流动并预测了抚州市人口的远期分配比例，据此得出，临川区作为抚州市政治、经济、文化以及教育的中心，无论是人口流动还是远期的人口占比与其他县相比都有显著的优势。

［1］ 陈彦光.人口流动的空间相互作用、Markov链和线性规划分析——地理研究中综合应用数学方法的一个实例［J］.信阳师范学院学报:自然科学版，2009，22（2）:216-221.

［2］ 张雯，靳军会.Markov链在中国人口年龄结构预测中的应用［J］.河南商业高等专科学校学报，2008，21（4）:45-48.

［3］ 360百科.抚州市［EB/OL］.http://baike.so.com/doc/5333731-5569168.html.2016-05-16.

［4］ Taylor P J. Quantitative methods in geography:an introduction to spatial analysis［M］.Illinois:Waveland Press，Inc，1983:2972302.

［5］ Wilson Α G. Entropy in urban and regional modelling［M］. London: Pion Press，1970.

［6］ Wilson Α G.地理学与环境:系统分析方法［M］.蔡运龙，译.北京:商务印书馆，1997.

［7］ Wilson Α G.Complex spatial system s:the modelling foundations of urban and regional analysis［M］.Singapore:Pearson Education Αsia PteLtd，2000.

Population flow analysis based on the spatial interaction model and Markova chain——Taking Fuzhou city,Jiangxi Province as an example

Αccording to regional economic development level， this article estimates the reasonable population of Fuzhou city， as the arrival quantity of spatial interaction model， and calculates the reasonable pattern of Fuzhou population flow by this model， and uses Markov chain to predict the future trend of Fuzhou population flow. Study shows that the population flow and long-term population proportion of LinChuan district have significant advantage in comparison to the rest county of Fuzhou.

Spatial interaction model； Markova chain； Fuzhou city

F241；C922

Α

1008-1151（2016）06-0135-04

2016-05-11

刘军辉（1989-），男，江西抚州人，东华理工大学地球科学学院硕士研究生，研究方向为土地资源管理、区域可持续发展。