立体几何“动态”问题处理策略

吴乐军

(四川省成都市中和中学，610212)



立体几何“动态”问题处理策略

吴乐军

(四川省成都市中和中学，610212)

立体几何中涉及空间点线面变动的问题,对空间想象力要求较高,学生难于把握,普遍感到无从下手.现举数例,对此类空间动态问题的处理策略进行提炼,但愿能助力大家对此类问题的理解．

策略1化空间动态为平面动态

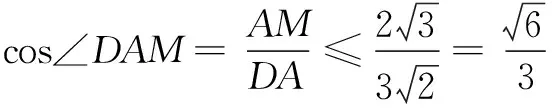
策略2依据“运动的相对性”化繁为简

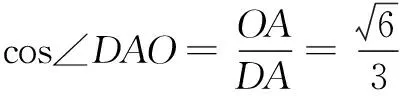
策略3纳入空间坐标，利用多变量设而不求转化

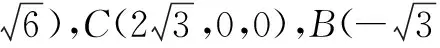
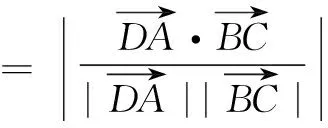
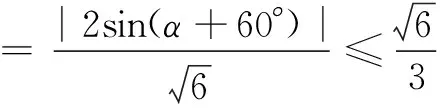
分析当MN为内切球的直径时，其长度最长，此时MN=2.建立如图6所示的空间直角坐标系，易知内切球的圆心为(1，1，1).由于MN可动，故设M(a,b,c),则N(2-a,2-b,2-c).设正方体表面的动点P(x,y,z)，则

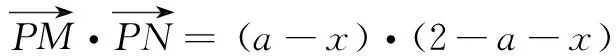
+(b-y)(2-b-y)

+(c-z)(2-c-z)

=(x-1)2+(y-1)2+(z-1)2

-[(a-1)2+(b-1)2+(c-1)2].

策略4依托空间基底，探究变量的相互关系

(A)存在某个位置，使得直线AC与直线BD垂直

(B)存在某个位置，使得直线AB与直线CD垂直

(C)存在某个位置，使得直线AD与直线BC垂直

(D)对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直

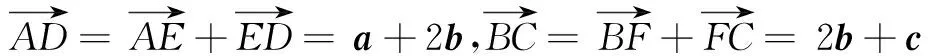
策略5恰当引入变量，视变量为常数寻求恒定关系建立函数获解

分析当正四棱锥V-ABCD绕着AB任意旋转时，它相对于平面α的位置可以通过平面VAB与平面α所成的锐二面角θ(30°≤θ≤90°)来体现.设线段CD的中点为M，线段AB的中点为N，当|CO|取得最大值时，V，C在平面α上的投影位于AB的异侧.

在Rt∆VON中，

|NO|=|NV|cos θ=2cos θ.

在Rt∆CMO中，

|MO|2=|MN|2+|NO|2

-2|MN||NO|cos(θ+60°)

故|CO|2=|CM|2+|MO|2

策略6以动制静，以静解动

例6已知点E，F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点，点M，N分别是线段D1E与C1F上的点，则与平面ABCD平行的直线MN有()

(A)0条(B)1条

(C)2条(D)无数条

分析如图9，将底面ABCD向上平移，与线段D1E，C1F必有交点，则两个交点的连线必与面ABCD平行，因此这样的直线有无数条，故选D.

例7正方体ABCD-A1B1C1D1中，与直线AA1,BD,C1D1同时相交的直线有()

(A)1条(B)2条

(C)3条(D)无数条

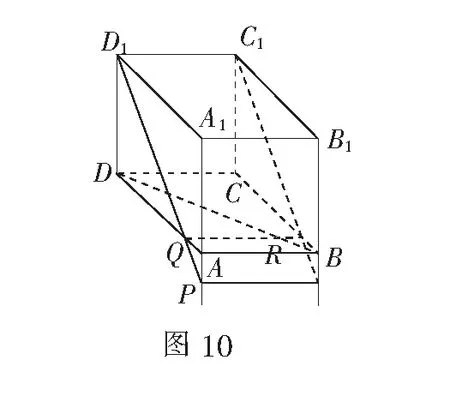
分析如图10，在线段A1A的延长线上任取一点P，则直线C1D1与点P确定一平面α，α与平面ABCD相交于直线QR，与直线BD交于点R.易知C1D1∥QR，而C1D1与PR必然相交，故在平面α内，存在直线PR能与直线AA1,BD,C1D1同时相交.当所取点P在线段A1P的延长线上变动时，将出现不同的直线PR，故符合条件的直线有无数条，选D.

策略7利用交轨法转化

例8(2015年浙江高考题)如图11，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是()

(A)直线(B)抛物线

(C)椭圆(D)双曲线的一支

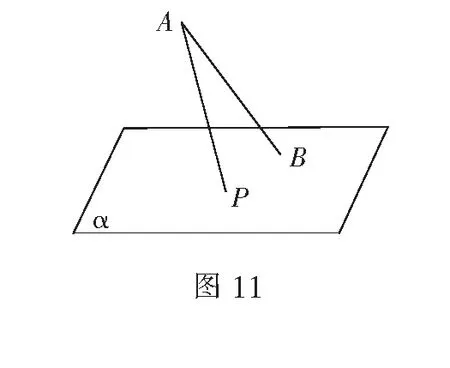
分析在空间中，假设AB垂直平面α，则满足条件的AP绕AB旋转形成一个圆锥，用一个与圆锥成60°角的平面截圆锥，所得图形为椭圆，故选C.

a·3n+1-a·3n=2a·3n=3n,