松弛型阻尼隔振模型的动刚度试验研究
刘兴天,钟 鸣,申军烽,周徐斌
(上海卫星工程研究所 空间机热一体化技术实验室,上海 201109)
松弛型阻尼隔振模型的动刚度试验研究
刘兴天,钟鸣,申军烽,周徐斌
(上海卫星工程研究所 空间机热一体化技术实验室,上海 201109)
针对松弛型阻尼隔振模型,从动刚度角度分析其与传统隔振模型的区别。通过求解松弛型阻尼隔振模型的传递率,说明系统最优传递率和动刚度的联系。使用波纹管提供刚度及密封,采用小孔阻尼结构形式,设计松弛型阻尼隔振器并对系统的阻尼系数求解。对所设计的松弛型阻尼隔振器进行了动刚度的测试,实验结果和理论预测吻合较好。研究对松弛型阻尼隔振器的优化设计具有很强的指导作用。
振动与波;松弛型阻尼;隔振器;动刚度;振动控制
随着航天事业的发展,一大批对地观测卫星、激光通讯卫星等即将立项研制。这些卫星的指向精度和分辨率等性能指标相比以往有了很大提高,其搭载的各种高性能载荷对星上微振动环境越来越敏感,在卫星平台的研制过程中,必须对微振动进行抑制[1-2]。微振动控制技术无疑将成为下一代高分辨率卫星的核心技术之一。
诱发航天器微振动的主要因素包括:星载各类转动部件高速转动、可控构件驱动机构工作、大型柔性构件进出阴影以及航天器变轨调姿期间,推力器的工作等[3]。这些振动分布频带广,幅值小,给控制带来很大困难。被动隔振器因可靠性高,实现性强,被各国广泛使用。宏观上来讲,隔振器的性能主要由刚度和阻尼决定。刚度控制着隔振系统的共振频率,而阻尼则控制着共振时的响应幅值。然而,阻尼的设计不能过大,因为较大的阻尼在降低共振峰值的同时,会使得隔振器在较高频的衰减效果降低。而阻尼过小则会引起共振峰的放大,不利于隔振。松弛型阻尼隔振器[4-5]能够克服以上矛盾,具有共振大阻尼,低频小阻尼的特性,近年来受到广泛关注[6-7]。明确松弛型液体阻尼隔振器的设计要点及机理对进行微振动控制具有重要意义。
本研究主要集中于松弛型阻尼隔振器的最优传递率及动刚度之间的联系,从动刚度试验出发,揭示松弛型阻尼隔振器的设计要点,为此类隔振器的设计提供指导。
1 松弛型阻尼隔振器模型
一般来讲,被动隔振器可以简化为图1(a)所示的刚度阻尼两参数Kevin模型[8],在Kevin模型的阻尼元件上串联一个松弛弹簧便组成了松弛型阻尼的三参数模型如图1(b)所示。

图1 隔振模型
隔振模型的动刚度定义为

Kevin模型的动刚度为

松弛型阻尼隔振模型的动刚度为
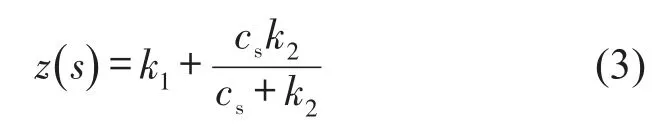
对于动刚度,代入s=jw,可以得到动刚度的模以及阻尼角。
不同阻尼系数下,典型的Kevin隔振模型和松弛型阻尼隔振模型的动刚度及阻尼角度分别见图2和图3。
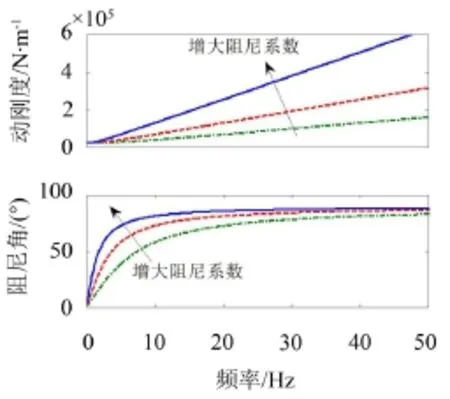
图2 阻尼系数对Kevin隔振模型动刚度和阻尼角的影响
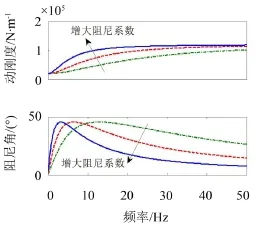
图3 阻尼系数对松弛型阻尼隔振模型动刚度和阻尼角的影响
从图中可以看出,相比于传统的Kevin隔振模型,松弛型阻尼的动刚度不会随着频率的增加而持续增大,同时,其阻尼角存在明显峰值。
实际上,松弛型阻尼隔振模型的这种特性使得其在高频时获得更好的振动衰减效果;而在共振处,若阻尼角和动刚度配合得当,能获得大阻尼所具有的良好共振峰抑制能力。
2 松弛型阻尼模型最优传递率
对于松弛型阻尼隔振模型,设被隔振物体的质量为m,不难推出其振动传递率的表达式[9]

阻尼系数对松弛型阻尼隔振系统传递率的影响如图4所示。

图4 松弛型阻尼隔振系统传递率以及对应的阻尼角
对于松弛型阻尼隔振模型,存在最优阻尼系数,使得传递率的峰值最小,即放大系数最小。而且传递率的峰值对应着松弛型阻尼隔振模型动刚度的阻尼角峰值。对于固定的隔振模型,其最优传递峰值为[9]

因此,获取松弛型阻尼隔振器的动刚度对于隔振系统的设计至关重要,只有准确获取隔振模型的动刚度,才能设计出共振放大系数最小,又保持高频衰减性能的隔振装置。
3 松弛型隔振器设计
使用波纹管来实现对液体的密封,上连接相对下连接运动时,液体通过小孔在阻尼腔之间流动产生阻尼力,对应图1(右图)中的阻尼系数c,阻尼腔的波纹管提供支撑刚度k1,缓冲腔对阻尼力进行缓冲,避免高频刚度硬化,缓冲腔的波纹管提供刚度k2。由于被隔振物体完全由k1承载,而单个松弛型隔振器的承载约为2 kg,固有频率为5 Hz,故尔将k1设计为2 000 N/m,而共振放大倍数应在1.5倍以下,根据前文最优传递率表达式,k2定位10 000 N/m。
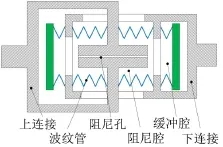
图5 松弛型阻尼隔振器设计原理图
两个波纹管的流体通过阻尼长孔流动产生阻尼力,如图6所示。

图6 阻尼长孔模型
设波纹管有效直径为D,阻尼通道直径为d,长度为L,流体的运动黏度为m。则隔振器被压缩的位移为x时,所产生的流体体积变化量为

设阻尼孔两端的压差为Δp,由流体的本构方程[10]可得
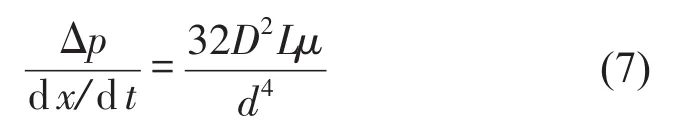
两端压差乘以小孔面积为阻尼力,阻尼系数和阻尼力成正比,可以得到阻尼系数C为[11]

4 动刚度实验
对所设计的松弛阻尼型隔振器进行实验研究,测试隔振器的动刚度,使用激振器产生正弦扫频激励,力信号使用力传感器采集,隔振器端部的位移由激光位移传感器测量。
针对两种隔振器进行试验,并选择不同的激励幅值进行测量。测得的隔振器动刚度曲线如图8和图9所示。

图7 松弛型阻尼隔振器动刚度测试图

图8 隔振器A动刚度曲线
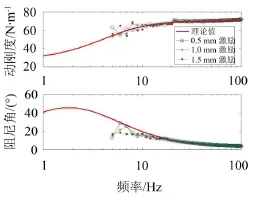
图9 隔振器B动刚度曲线
两个隔振器的阻尼系数分别为CA=2 000 N(m/s)和 CB=3 000 N(m/s),对 应 的 KA=2 000 N/m,KB=10 000 N/m。从图中可以看出,阻尼系数的设计值和试验值吻合良好,且激励幅值对阻尼系数的影响有限。由于所采用的激振器低频效果欠佳,因此没有取得5 Hz以下动刚度数据。但不影响使用该方法进行松弛型阻尼隔振器的设计。
5 结语
(1)采用松弛型阻尼隔振器进行振动控制能够获取良好的高频衰减性能以及较小的共振峰值,松弛型阻尼隔振器在取得最优传递率时,其对应共振频率处的动刚度阻尼角达到最大值。
(2)松弛型阻尼隔振器的动刚度测试曲线和理论预测值吻合良好,激励幅值对隔振器的动刚度影响较小,系统呈现良好的线性特性。
(3)在工程使用此类型隔振器时,应进行动刚度计算及试验,获取隔振器动刚度及阻尼角参数,进而获取具有最优传递率的隔振器。
[1]董瑶海.航天器微振动—理论与实践[M].北京:中国宇航出版社,2015.
[2]孙晓芬,杨斌堂,赵龙.巨磁致伸缩自适应精密驱动和振动控制[J].噪声与振动控制,2014,34(5):16-21.
[3]石新宇,周徐斌,申军烽,等.航天器电磁变频吸振器性能分析与测试[J].噪声与振动控制,2015,35(5):60-64.
[4]DAVIS P,CUNNINGHAM D,HARRELL J.Advanced 1.5 Hz passive viscous isolation system[C].Procedings of the 35thAIAA/ASME/ASCE/AHS/ASC structures,structural dynamics and materials conference,Hilto Head,SC,USA:2655-2665,1994.
[5]ZHANG Y,ZHANG J,XU S.Parameters design of vibration isolation platform for control moment gyroscopes[J].ActaAstronautica,2012,81(2):645-659.
[6]DAVIS L P,WILSON J F.Hubble space telescope reactionwheelassemblyvibrationisolationsystem. Structural dynamics and control interaction of flexible structures[R].NASAReport N87-22702(1986):669-690.
[7]WILSON G W,WOLKE P J.Performance Prediction of DStrut Isolation Systems[C].Passive Damping and Isolation Conference,San Diego CA,March:3-4,1997.
[8]丁旭杰.非线性隔振抗冲器的设计与建模研究[D].上海:上海交通大学,2008.
[9]丁文镜.减振理论[M].北京:清华大学出版社,1988.
[10]盛敬超.液压流体力学[M].北京:机械工业出版社,1980.
[11]杨庆俊,廖蕾.波纹管式流体阻尼隔振器研究[J].液压与气动,2006(7):27-28.
ExperimentalAnalysis of the Dynamic Stiffness of a Vibration Isolation System with Relaxation Type Damping
LIU Xing-tian,ZHONGMing,SHEN Jun-feng,ZHOU Xu-bin
(Laboratory of Space Mechanical and Thermal Integrative Technology,Shanghai Institute of Satellite Engineering,Shanghai 201109,China)
The dynamic stiffness of a virration isolation model with relaxation type damping is deduced and compared with that of a traditional Kelvin vibration isolation model.The relationship between the transmissibility and dynamic stiffness of the relaxation type damping vibration isolation model is discussed.The isolator with relaxation type damping is designed by adopting bellow and small hole to generate the damping force.The damping force is obtained analytically for the small holes.The dynamic stiffness of the designed isolator is measured experimentally.The result is found to be in good accordance with the theory.This research is of significant guidance for optimal design of the relaxation type damping isolators.
vibration and wave;relaxation type damping;vibration isolator;dynamic stiffness;vibration control
TH133.1;TB535;TP273
ADOI编码:10.3969/j.issn.1006-1335.2016.05.037
1006-1355(2016)05-0180-03+200
2016-02-25
国家自然科学基金资助项目(51505294);上海市科委资助项目14XD1423000
刘兴天(1984-),男,江苏省徐州市人,博士,主要研究方向为非线性动力学、结构振动控制。E-mail:xtliu509@126.com

