基于加速老化试验的IGBT寿命预测模型研究

张亚玲，李志刚

（河北工业大学电气工程学院，天津 300130）

基于加速老化试验的IGBT寿命预测模型研究

张亚玲，李志刚

（河北工业大学电气工程学院，天津 300130）

绝缘栅双极型晶体管（insulated gate bipolar transistor，IGBT）在工作过程中经常要承受过热和较大的温度波动，当热损伤达到一定程度时，模块极有可能出现失效，这会给电力系统造成巨大的危害。如果能根据寿命预测模型提前预估模块的寿命，便可以在模块即将失效之前进行更换，从而避免模块突然失效带来的损失。因此，考虑在检测模块壳温的条件下进行IGBT的温度循环试验，研究工况中易获得的壳温与IGBT寿命的关系模型。在已有寿命模型的基础上，提出改进的寿命预测模型，经试验数据验证准确度更高。

绝缘栅双极型晶体管；温度循环；寿命预测模型

在智能电网建设的大背景下，IGBT作为新型电力电子器件的典型代表，在智能电网的相关设备如光伏逆变器、风能变流器、储能逆变器、柔性直流换流阀等中起着至关重要的作用［1］。

IGBT经常工作在过载、过热等恶劣环境中，当受到电应力或热应力的反复冲击时，会发生疲劳损伤，引发器件失效［2］。以往文献主要以结温为主要对象研究IGBT在功率循环下的寿命［3］，其中应用较广泛的是Coffin-Manson模型［4］和LESIT模型［5］。实施功率循环试验的基本问题是试验条件的选取，由疲劳损伤理论可知在给定正向电流和试验持续时间ton的条件下，目标ΔTj是耗散能量和热阻的函数，所以很难在完全相同的试验条件下重复一个试验。并且，功率循环寿命预测模型中结温为IGBT内部芯片的最高温度，工况下很难获得，因此，本文考虑在监测模块壳温的条件下进行IGBT的温度循环试验，研究工况中更易获得的壳温，探索壳温与IGBT寿命的关系模型。

1 加速试验应力的确定

正常工作情况下IGBT模块的寿命约为10 a，在正常工作下研究其退化规律花费时间过长，因此考虑加速老化实验。产品加速寿命试验的应力确定主要包括应力的类型、施加方式、施加范围等内容。

1）应力类型。IGBT在使用过程中主要受电应力和热应力的影响。文献［6］指出，近60%的器件失效由热应力引起，因此本文中加速寿命试验将选取温度作为加速试验的应力类型。

2）应力施加方式。根据应力变化形式的不同，常见的加速寿命试验应力施加方式有恒定应力、步进应力和序进应力。由于恒定应力加速试验具有试验方法简单、试验设备要求不高、试验理论较为成熟等优点，因此本文采用恒定应力的施加方式，即将IGBT在固定的温度波动速率下进行寿命加速试验。

3）应力施加范围。器件在承受过应力（包括过压、过流、过热及过高的电流上升率di/dt与过高的电压上升率du/dt等）时会引发器件失效。器件工作在额定应力下时，当受到电应力或热应力的反复冲击时，会发生疲劳损伤。损伤达到一定程度会导致焊料层出现裂纹与空洞、键合引线发生熔化导致脱焊、金属表面产生剥离等情况，使得器件可靠性下降，引发器件失效。其中额定应力范围内的失效更能反映器件实际的老化过程，因此选择温度范围为40～100℃（不超过器件的极限值130℃），通过加速温度的波动速率来加速器件的老化，从而在不改变器件失效机理的情况下，进行加速老化试验。

2 实验原理和实验平台

2.1 试验方案

图1所示为加速老化实验的电路原理图，图中DUT为试验器件；PWR为程控试验电源5 V/ 300 A；VG为G脚程控电0～15 V；RG为G脚串联电阻10 Ω/2W；RIS为电流互感器0～300A。

图1 IGBT老化实验电路图Fig.1 Electrical circuit of IGBT accelerated aging test

试验方案如下：对6个IGBT模块进行温度循环老化试验，试验条件设置如表1所示，其中N为试验模块序号；IC为加热电流（A）；ΔTc为壳温波动范围，测试模块在不同试验条件下失效前的温度循环周期数。

表1 加速寿命试验方案Tab.1 The program of accelerated lifetime test

2.2 加速老化试验平台

加速老化实验系统采用上位机控制方式。系统配置10个相对独立的老化实验区，每个老化实验区由加热电路（提供0～300 A直流电流）、驱动电路（提供0～20 V的驱动电压）和冷却系统（风机和散热器）组成。模块底部装有温度探头，可以将铜底板温度实时传递给上位机，再通过上位机中的程序控制IGBT的通断，以40～90℃为例，铜底板温度达到90℃后模块进入关断状态，在散热器的作用下，模块不断冷却到40℃后模块重新导通，使模块重复相同的温度循环过程。表2为加速寿命试验的试验结果。

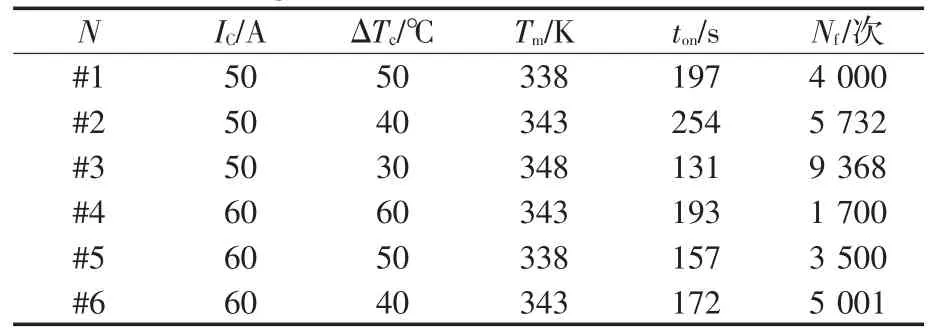
表2 IGBT模块加速寿命试验数据Tab.2 The figure of IGBT model accelerated lifetime test

3 IGBT寿命预测模型研究

3.1 基于功率循环的IGBT寿命预测模型研究

3.1.1 Coffin-Manson模型

Coffin-Manson模型能很好地表征材料在周期性应力作用下发生疲劳及随疲劳程度增加而导致材料变形和断裂的过程。这个过程与IGBT模块失效过程一致，比如焊接层的疲劳破裂和键合引线的断裂等。因此广泛运用于功率循环下的IGBT寿命预测。

这个基本的寿命预测模型假设模块功率循环次数NfJ只与结温变化幅度有关，模块寿命可以用下式来预估：

其中，NfJ为模块的功率循环次数；α和n为能够反映材料塑性应变能力和实验中器件周期性疲劳程度的常数，这2个数据可以通过实验数据拟合得到。模型中器件的寿命仅受到结温变化范围ΔTj的影响，因此误差较大。

3.1.2 LESIT模型

20世纪90年代初期实施了一个确定标准模块寿命的项目。这个命名为LESIT的项目，对欧洲和日本等不同供应商的模块进行试验，探究IGBT的寿命预测模型。研究发现循环温度的平均值对器件的寿命有显著影响，模块循环寿命可看作是结温变化幅度和平均结温的函数，如下式：

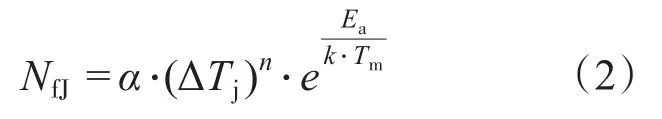
式中：Ea为硅芯片激活能，Ea=7.8×104J/mol；k为气体常数，k=8.314 J/mol；Tm为平均结温，K；α，n为常数，由试验数据拟合得到。

该模型包含Coffin-Manson模型和表征温度绝对值的平均结温，比Coffin-Manson模型能更好地描述模块的失效机制。然而该模型不能反映焊料失效过程，因为焊料的疲劳受周期时间和形状（温度保持时间、上升下降时间）的影响。

3.2 基于温度循环的IGBT寿命预测模型研究

考虑到功率循环与温度循环对器件寿命的影响有一定的相似性，首先考虑运用已有的功率循环寿命预测模型，用壳温变化幅度替代结温变化幅度对温度循环试验结果进行预测分析。

3.2.1 Coffin-Manson模型

采用最小二乘法，以Coffin-Manson模型为基础，对表2所示的加速寿命试验数据进行拟合，得到α=22 140，n=-2.258 8，相应的寿命预测模型M1为

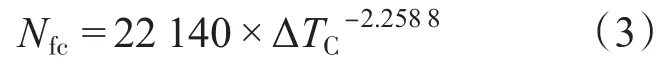
式中：Nfc为模块温度循环周期数；ΔTC为壳温波动范围。

3.2.2 LESIT模型

以LESIT模型为基础，对表2所示的加速寿命试验数据进行拟合，得到α=7.266 5×10-4，n=-3.126 3，相应的寿命预测模型M2为

由图2可知，基于Coffin-Manson模型的M1反而比基于LESIT模型的M2有更高的预测精度，这与功率循环寿命预测模型的结果不符，分析可能是因为功率循环中每次循环时间较短（一般为几s），而温度循环中每次循环时间较长。因此，考虑提出含有导通时间的改进模型探讨平均温度对寿命的影响。

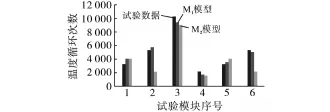
图2 寿命预测模型结果对比图Fig.2 The contrast diagram of different lifetime prediction models

3.2.3 改进模型

考虑到Coffin-Manson模型和LESIT模型没有涉及加热电流和循环时间，而这些都是影响模块寿命的因素，因此提出包含更多参数的改进模型。器件寿命不止受温度的波动范围影响，也会受温度变化速率影响，而在本次试验中模块的导通时间和关断时间均与循环温度和试验环境有关，且关断时间在循环温度和试验环境一定的情况下，为1个定量，所以模型中加入导通时间参量，忽略通断时间。故在Coffin-Manson模型的基础上提出改进的寿命预测模型M3为

式中：ton为每个温度循环中IGBT模块的导通时间，s；ΔTC/ton为温度变化速率；IC为加速寿命试验中模块的加热电流；n1，n2，n3，n4为未知参数，由试验数据拟合得到。

为分析平均温度在温度循环中对寿命的影响，在LESIT模型的基础上提出改进的寿命预测模型M4为

式中：n1,n2,n3,n4为未知参数，由试验数据拟合得到。

利用表2数据对模型M3作最小二乘法拟合，得n1=551526，n2=-0.0119，n3=-2.0318，n4=-1.022，得到M3为

利用表2数据对模型M4作最小二乘法拟合，n1=1.91×10-3，n2=-0.087 1，n3=-2.984 2，n4=-0.406 2得到M4为

4 寿命预测模型对比分析

各个寿命预测模型的结果对比如表3所示。

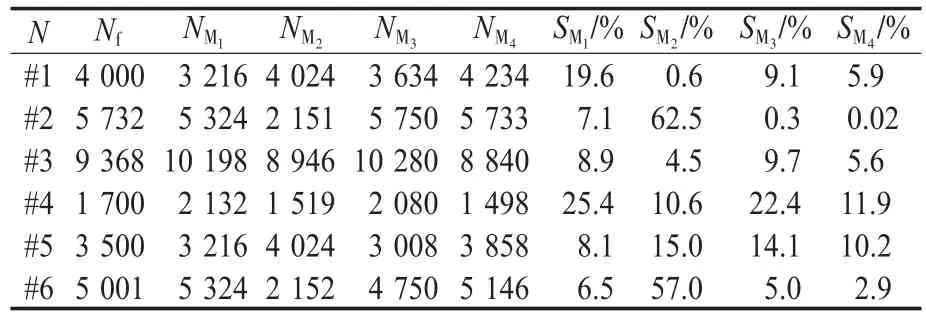
表3 加速寿命试验误差分析Tab.3 The error analysis of accelerated lifetime test

表3中，NMi（i=1，2，3，4）分别为模型M1，M2，M3，M4在对应序号试验条件下的预测值，为模型预测值对应序号试验条件下的误差，为了能更直观地看出各个模型的优劣性，设

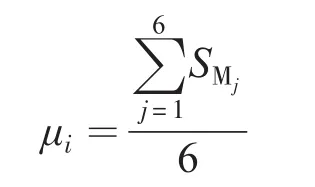
式中：i为预测模型的编号，i=1，2，3，4；j为试验模块的序号，j=1，2，3，4，5，6；μi为各个模型的平均误差，计算得到 μ1=9.3%，μ2=25%，μ3= 10.1%，μ4=6.5%。

Coffin-Manson模型只考虑温度波动值对器件寿命的影响，参数单一，精度不高。LESIT模型为Coffin-Manson模型的修正模型，将温度的绝对值（平均壳温）考虑进去，在功率循环的寿命预测中拥有更高的预测精度。但由试验结果分析可知在基于温度循环的试验中LESIT模型却比Coffin-Manson模型预测精度低，为验证温度循环中带有平均壳温的指数项是否对器件寿命有影响，比较寿命预测模型M3和M4，通过试验结果发现，有平均壳温参数的模型M4比没有平均壳温参数的模型M3预测精度更高。因此，在温度循环试验中平均壳温依然对器件寿命有影响，至于LESIT模型比Coffin-Manson模型预测精度低可能是因为平均温度对器件寿命的影响被其他因素所掩盖。

寿命预测模型均是基于相同重复的功率周期，但在实际应用中模块的损伤往往是由各种不同的功率周期累加而成。针对这一问题，文献［8］中学者提出采用线性疲劳损伤积累理论，即Miner定理，预测不同ΔTj周期的共同作用效果。但Miner定理假设不同ΔTj周期的作用效果是相同的，而文献［9］则表明具有高ΔTj的周期在器件失效中起主导作用。一个更好的办法是采用雨流计数法，运用雨流计数法进行寿命预测，首先需要将产品的任务曲线转换成温度曲线。然后将实际温度曲线简化成比较规则的曲线，采用雨流法对温度循环计数，根据模型采用作出寿命预测。文献［10］表明利用Miner规则和雨流法，可以估算系统在复杂工作状态下的疲劳寿命。建立可靠的寿命预测模型后，可参考功率周期中疲劳累积理论，计算模块实际运行中的等效疲劳损伤，从而实现工况下模块剩余寿命的预测。

5 结论

加速寿命试验结果表明将功率循环的寿命预测模型运用于温度循环寿命预测时，Coffin-Manson模型比LESIT模型有更高的预测精度。但添加了加热电流和模块导通时间后有平均温度指数项的改进模型M4在温度循环的寿命预测中有更好的适应性。

［1］金锐，于坤山，张朋，等.IGBT器件的发展现状以及在智能电网中的应用［J］.智能电网，2013，1（2）：11-16.

［2］BERG H，WOLFGANG E.Advanced IGBT Modules for Railway Traction Applications：Reliability Testing［C］//9th European Symposium on Reliability of Electron Devices，Failure Physics and Analysis（ESREF1998），1998：1319-1323.

［3］Marco Denk，Bakran Mark-M.Comparison of Counting Algorithms and Empiric Lifetime Models to Analyze the Load-profile of an IGBT Power Module in a Hybrid Car［C］//Electric Drives Production Conference（EDPC），2013 3rd，2013：1-6.

［4］杜熠，李璠，曾照洋，等.IGBT性能退化模型构建方法研究［J］.电力电子技术，2013，47（1）：104-106.

［5］Hamidi A，Beck N，Thomas K，et al.Reliability and Lifetime Evaluation of Different Wire Bonding Technologies for High Power IGBT Modules［C］//10th European Symposium on Reliability of Electron Devices，Failure Physics and Analysis（ESREF1999），1999：1153-1158.

［6］Fabis P M，Shum D，Windischmann H.Thermal Modeling of Diamond-based Power Electronics Packaging［C］//Proceeding of Fifteenth IEEE Semiconductor Thermal Measurement and Management Symposium.Piscataway，NJ，USA：IEEE，1999：98-104.

［7］Held M，Jacob P，Nicoletti G，et al.Fast Power Cycling Test of IGBT Modules in Traction Applica-tion［C］//Power Electronics and Drive Systems，1997：425-430.

［8］Miner M A.Cumulative Damage in Fatigue［J］.Applied Mechanics，1945（12）：159-164.

［9］Feller M，Lutz J，Bayerer R.Power Cycling of IGBT Modules with Superimposed Thermal Cycles［C］//Proceeding of the PCIM，2008：1-6.

［10］Matsuishi M，Fndo T.Fatigue of Metals Subjected to Varying Stress-fatigue Lives Under Random Loading［C］//Proc of the Kyushu District Meeting.The Japan Society of Mechanical Fngineers，1968：37-40.

Research on IGBT Lifetime Prediction Models Based on Accelerated Lifetime Test

ZHANG Yaling，LI Zhigang
（School of Electrical Engineering，Hebei University of Technology，Tianjin 300130，China）

Insulated gate bipolar transistor（IGBT）often works in overheating and large temperature fluctuating conditions，when the heating damage accumulates to a certain degree，the failure of IGBT module is most likely occur，which leads to huge losses in electric system.If we can estimate the life of the module according to lifetime prediction model，the module can be replaced before it is going to fail，so it is possible to avoid losses caused by sudden failure of the module.Therefore，the IGBT temperature cycling test was done and the case temperature was detected simultaneously，then researched the relationship between IGBT lifetime and case temperature which was more accessible.Based on the existing life models，provided an improved lifetime prediction model which is proved having the higher accuracy.

insulated gate bipolar transistor（IGBT）；temperature recycle；lifetime prediction models

TM322

A

10.19457/j.1001-2095.20161016

2015-09-07

修改稿日期：2016-04-11

国家科技支撑计划资助项目（2015BAA09B01）；河北省科技支撑计划资助项目（13214303D；14214503D）

张亚玲（1988-），女，研究生，Email：yaling_zhang616@163.com