光学中三个疑点问题的教学处理

张修文

摘 要：如何引导学生进行合作学习、科学探究，怎样有效培养学生良好的思维品质、严密的逻辑推理和较强的定性分析能力，如何运用知识解决遇到的问题等是物理教学中应该高度重视的问题。本文以光学中学生的三个疑点问题的教学处理为案例，就操作层面上记录成文。

关键词：问题提出；实验观察；递进引导；自主学习；合作研究

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2016）8-0066-3

1 疑点一：在水面上方看到的水中物体像的位置究竟在哪里？它与眼睛的位置有关吗？

在高中光学新课教学中，提出上述问题时总是听到不少“在物体正上方”的回答。于是，笔者拿出了从水产市场借来的无盖容器（底和壁都不透明），盛满水后再放进一枚石子，让学生仔细观察现象并把离容器近些观察到的像的位置和离得远些观察到的位置作比较，看有没有变化，怎样变化？

学生通过观察，初步获得了如下结论：对于水下的同一物体，不同的观察者看到的情况具有相同的成像规律——像变浅（像向水面靠近）、变近（向观察者靠近）；但变浅、变近的程度随眼睛位置变化，眼睛的位置越偏，像的位置就越浅、越近、越模糊。

用实验获得了初步结论后，笔者并不急于给学生作理论分析，而是把学生分成几个研究小组，让各组在课后进行研究、讨论，作出定性的理论分析，以待日后在课堂上与全体同学一起研究。

经过学生在课后的研究，有的研究小组写出了定性分析的实验报告，整理抄录如下：如图1所示，水下的物体S（以点表示）入射到水面上靠得极近（才能进入人眼瞳孔）的两条光线的入射点为A1、A2，入射角分别为θ1、θ2；对应其折射光线和折射角分别为A1B1、A2B2和β1、β2。由折射规律知 β1>θ1、 β2>θ2、 β2>β1，所以，两折射光线A1B1、A2B2的反向延长线的交点，即人眼所见像S'的位置必然向上和向前移动；当人眼越偏，能进入眼睛的光线的入射点A1、A2就离O点越远，折射角β1、β2就越大，两折射光线A1B1、A2B2的反向延长线的交点，即人眼所见像S'的位置就向上和向前移动越多，同时反射光线越强，能进入人眼的折射光线越弱，所以像越模糊。

对观察到的实验结论找到了充足的理论依据之后，学生们的研究热情高涨。又有人提出：“像能在物体的正上方吗？应在什么位置观察？”的问题。

在前述研究的基础上，很快便有研究小组找到了理论上的结论：在物体的正上方观察时，像就在物体的正上方。理由如下：当眼睛在物点正上方观察时，进入眼睛的任何一条光线都必有一条关于y轴的对称光线，这些对称光线的折射光线也关于y轴对称，而所有折射光线的反向延长线相交的点（像点）就在y轴上，但比像的位置高。这个理论分析得到了所有学生认可的时候，我们又用前述实验进行检验。

至此，通过学生们共同参与研究，在研究中相互学习，相互从思考中提示、补充和完善，对水中物体像的位置作了较深入的定性研究，并获得了较完善的定性结论，取得了好的效果。

2 疑点二：光速之快，人类初期是怎样测出来的呢？

面对学生提出的问题，笔者推荐了经全国中小学教材委员会2002年审查通过，人民教育出版社出版的全日制普通高中教科书（必修加选修）《物理》第3册阅读教材“光速的测定”内容中美国物理学家“迈克耳逊的旋转棱镜法测光速”的实验。

学生阅读后又问：迈克耳逊是怎样在八面镜的高速旋转中选择出符合要求的转速的？

针对学生的问题，笔者让学生再仔细阅读下述推荐材料并思考、讨论后面两个梯级递进的问题。

材料内容：

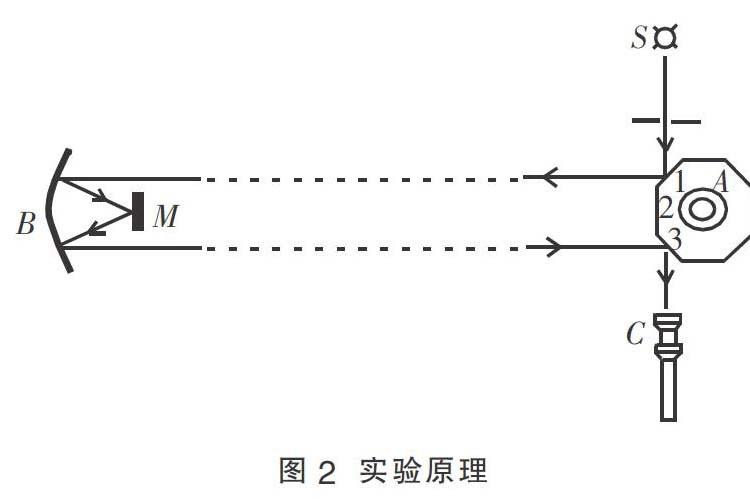
如图2，迈克耳逊选择了两座山峰，测出两山峰间的距离，在第一个山峰上安装一个强光源S和一个正八面棱镜A。光源S发出的光，经过狭缝射到八面镜A的面1上，反射后射到放置在另一个山峰上的凹面镜B上，又反射到平面镜M上，经过M反射后，再由B反射回第一个山峰。如果八面镜静止不动，反射回来的光就射到八面镜的另一个面3上，经面3反射后，通过望远镜C进入观察者的眼中，看到光源S的像。

如果使八面镜转动。那么，光反射回来时八面镜的面3已经偏离了原来的取向。经面3反射后的光不再进入望远镜中，观察者就看不到光源S的像了。适当调节八面镜的转速。使反射回来的光到达八面镜时，八面镜恰好转过1/8转，面2正好转到面3原来的位置，经面2反射后的光进入望远镜中，就可以重新看到S的像。根据八面镜转过1/8转所用的时间和两山峰间的距离，就可以算出光在空气中的速度。

两个递进引导的问题：

（1）在八面镜尚未转动时用望远镜观察到光源的像之后，当八面镜在转动过程中，仍要由转到原来面3位置的反射面反射光线进入望远镜而重新看到S的像的话，望远镜还能移动位置吗？

（2）迈克耳逊是如何在八面镜的高速旋转中选择出了符合“光在两山仪器间往返的时间内恰转1/8转”的转速要求的？

同学们经过再次阅读并思考，很快明确了：当八面镜在转动过程中，仍要由转到原来面3位置的反射面反射光线进入望远镜而重新看到S的像的话，则望远镜必须固定不动。

接下来，同学们各抒己见，充分研究和讨论后又明白了：当望远镜固定不动，旋转八面镜仍能从望远镜中再次观察到光源的像，八面镜的旋转速度必须是在光传播时间内转过1/8转、1/4转、3/8转、1/2转、5/8转……要能“重新见到光源S的像”时，八面镜的最低转速应该是1/8转。

至此，笔者引导学生得出了：迈克耳逊正是把能“重新见到光源S的像”时，八面镜的最低转速确定为“符合要求的转速的”。

实际上，光速之大，在有限的地面实际距离传播时间很短，要求八面镜具有极高转速的技术难度很大，迈克耳逊在测定光速的一次实验中，测得两山峰间的距离为35373.21米，从望远镜中看到光源的像时，八面镜的最低转速达到了528转/秒。如果还要提高八面镜的转速，技术要求会更高，而最容易做到的，是重新见到光源S的像时，八面镜恰好转过1/8转，对应八面镜的转速最低。因此，也可以说迈克耳逊是把最容易“重新见到光源S的像”时，八面镜的转速确定为“符合要求的转速的”。

3 疑点三：利用光的干涉检查平整度时，如何从条纹弯曲方向判定被检平面在此处是凹下还是凸起？

在经全国中小学教材委员会2005年初审通过，人民教育出版社出版的普通高中课程教材实验教科书《物理》选修3-4第十三章第七节的“科学漫步”栏目中“利用光的干涉检查平整度”阅读材料部分中，有关于条纹弯曲方向与被检表面凹凸情况的判定问题。

针对学生不清楚的现象，笔者仍然采取了以下分层递进的教学方法与学生讨论，学生反应良好。

如图3所示，若被检表面为平面，空气层厚度相同的各点就位于一条直线上，产生的干涉条纹（以亮纹为例）是平行的直线（设在图中aa1、bb1、cc1上方）；而出现亮纹的地方空气层厚度d与照射的单色光波长λ之间的关系为：2d=kλ，式中k=0、1、2……即出现相邻亮纹处的空气厚度差Δd都为λ/2，由数学易知这些位置间必然等间距（即，ab=bc）。所以，若被检表面为平面，干涉条纹为等距离平行直条纹。

若在图3被检表面原来产生亮条纹的b位置出现凹陷，则原来在该处的亮纹移动到与原来空气层等厚度的地方。如图4所示，由平行线间各处距离相等，过原b点作标准样板OA的平行线与凹陷面相交于b1'，再过b1'作bb1的平行线与OA交于b2'，则原来在bb1上方的亮纹移动到b1'b2'的上方。即，有凹陷时条纹向劈尖方向弯。

同理，若在图3被检表面原产生条纹的b位置出现凸起，如图5所示，由平行线间各处距离相等，过原b点作标准样板OA的平行线与凸起面相交于b1'，再过b1'作bb1的平行线与OA交于b2'，则原来在bb1上方的亮纹移动到b1'b2'的上方。即，有凸起时条纹向远离劈尖方向弯。

参考文献：

[1]人民教育出版社物理室.全日制高级中学教科书（必修加选修）第三册 物理[M].北京：人民教育出版社，2002.

[2]人民教育出版社物理室.高级中学实验课本（修订本）第一册 物理[M].北京：人民教育出版社，1995.

[3]人民教育出版社物理课程教材研究开发中心.普通高中课程标准实验教科书（选修3-4） 物理[M].北京：人民教育出版社，2010.