掀开你的红盖头
——利用通性通法对一道联考题的探究与推广
张 琳
安徽省凤阳县临淮中学 (233100)
掀开你的红盖头
——利用通性通法对一道联考题的探究与推广
张琳
安徽省凤阳县临淮中学(233100)
解题是数学教学的重要组成部分,解题技巧是绕不开的话题,波利亚说过“问题是数学的心脏,解题是数学的灵魂,掌握数学意味着就是善于解题”.考试大纲明确指出:“考查时要从学科整体意义和思想含义上立意,注重通性通法,淡化特殊技巧.”为此笔者和学生一起从通性通法的这一角度对一道期末联考题进行探究与推广.

一、小荷才露尖尖角
二、乱花渐欲迷人眼

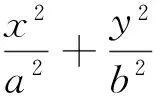
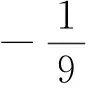
“猜想只合‘情’但未必就合‘理’,正确的结论需经过严格地推理论证,请同学们尝试一下能否证明?”
同学们纷纷行动,由于对于本题通性通法的解题操作已经熟练,稍后一位性格内向的学生4给出了推导过程,简录如下.
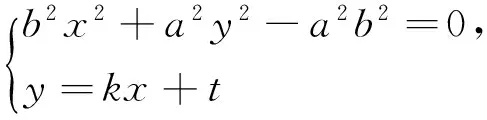
(b2+k2a2)x2+2a2ktx+a2t2-a2b2=0,
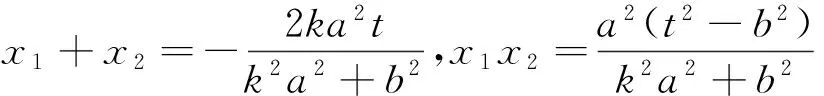
对这位同学的较强计算能力给予了高度地赞扬,随即提出:“这位同学的推理步骤中是否有漏洞?”
学生5:应考虑直线MN方程的斜率不存在情形.“ 能否加以验证?”
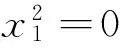
太棒了!命题1终于甩掉了“猜想”的帽子,名正言顺地跨入“定理”的行列.
三、万紫千红总是春
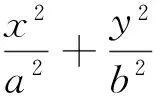
命题7已知P是抛物线Γ: y2=2px(p>0)顶点,M、N是抛物线Γ上异于点P的不同两点,且满足PM⊥PN.则直线MN恒过定点(2p,0).
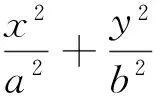
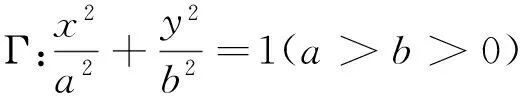

命题10已知P(x0,y0)是抛物线Γ: y2=2px(p>0)任意一点,M、N是抛物线Γ上异于点P的不同两点,且满足PM⊥PN.则直线MN恒过定点(x0+2p,-y0).
既然椭圆、双曲线及抛物线的方程可统一表述成二次曲线方程Ax2+By2+Cx+Dy+E=0(A2+B2≠0)形式,上述10个命题能否进一步推广呢?这时下课铃已响,带着这个疑问笔者果断决定继续完成余下的推广工作,部分同学表现出同样饱满的探究热情,加入“探险”行列.
四、众里寻他千百度
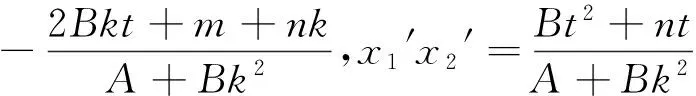
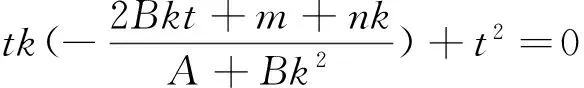

五、掀开你的盖头来
学生的脸上绽放出幸福的微笑,于是一个重要的结论千呼万唤始出来.
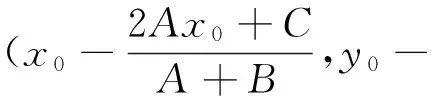

掀开你的红盖头,原来的你如此美丽.

