一类二元二次函数取值范围问题的几何解法

祁学军

宁夏中卫市中宁县大战场镇北滩小学　(755100)



一类二元二次函数取值范围问题的几何解法

祁学军

宁夏中卫市中宁县大战场镇北滩小学(755100)

1.引言

类似“实数x,y满足Ax2+Bxy+Cy2=D(D≠0)，求S=ux2+vxy+wy2的取值范围”的问题在各级各类数学竞赛中经常出现，而且在各类数学报刊杂志中给出了不同的解法(如文[1]、[2])．最近文[3]用三角换元法给出了此类问题的又一新解法，并指出三角换元是处理这类问题的比较有效的一般方法．本文笔者再通过构造直线与圆锥曲线，利用直线与圆锥曲线的位置关系简单而巧妙的解决这一问题，供大家参考．

2.应用举例

例1(2011年浙江理科第16题)设x,y∈R，若4x2+y2+xy=1，则2x+y的最大值是 ．

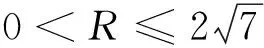
例3(2006年安徽省高中数学竞赛初赛题)设x,y是实数且满足x2+xy+y2=3，则x2-xy+y2的最大值与最小值是.

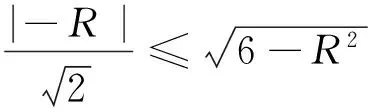
例4(1997年莫斯科大学化学系入学考试数学试题)设x2-xy+2y2=1，求表达式x2+2y2的最大值与最小值．

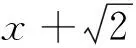
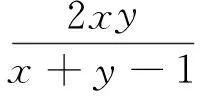
为进一步掌握此类问题的几何解法，下面再给出几个例子．

例7(1993年全国高中数学联赛试题)

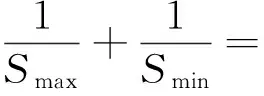
例8(2001年全国初中数学竞赛题)已知实数a,b满足a2+ab+b2=1，且t=ab-a2-b2，则t的取值范围是．

例9(1998年湖北黄冈市初中数学竞赛题)已知实数a,b满足a2+ab+b2=1，求a2-ab+b2的取值范围．

3.结语

由上可知，只要我们根据已知条件和所求式子的特征，联立方程组，把问题转化为含有Ax+By+C=0(A2+B2≠0)和ux2+vy2=w(uv≠0)，然后构造直线与圆锥曲线方程，问题就会迎刃而解．当然，这样的例子还有很多，请大家继续研究和探讨．

[1]张勇赴，姜官扬．一类二元二次函数的取值范围问题之通解[J]．中学数学教学参考(上旬)，2009(9)．

[2]蔡祖才．一类二元二次函数的取值范围的统一解法[J]．高中数学教与学，2011(8)．

[3]查正开．一类二元条件函数取值范围问题的解法研究[J]．中学数学月刊，2012(4).