一道课本数列题解法的探究

白亚军

甘肃省永昌县第一高级中学　(737200)



一道课本数列题解法的探究

白亚军

甘肃省永昌县第一高级中学(737200)

人教A版《必修5》第二章数列复习参考题B组第6题如下:

已知数列{an}中,a1=5,a2=2,an=2an-1+3an-2(n≥3),对于这个数列的递推公式作一研究,能否写出它的通项公式?

点评:递推公式是给出数列的一种常用方法,由递推关系式求数列的通项公式,方法多样,而本题解析过程是教师教学用书的解法,下面总结递推公式an+2=pan+1+qan(其中p≠0,q≠0的常数)求通项公式的方法,采用构造法,转化为新的等差或等比数列.

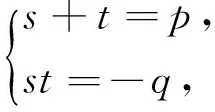
下面通过例题对这一问题进行具体探究.

(1)求数列{an}和{bn}的通项公式；

(2)记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn

本文仅对数列{an}的通项公式的求解作一探讨.

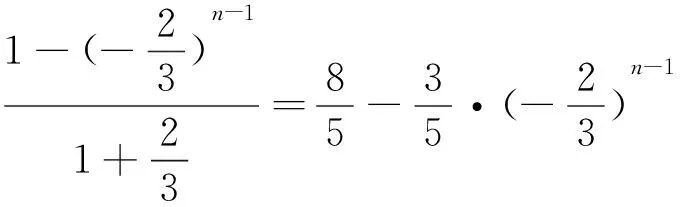
点评:转化是求解递推数列通项的通性通法,从近年来的高考题中时有出现,因而在教学中注意对这类问题进行归类解析.

人教A版《必修5》第二章数列p32阅读与思考中提到斐波那契数列,斐波那契数列是从动物的繁殖问题引出的,满足的就是递推公式an+2=pan+1+qan,下面从高等数学角度进行探究,而构造法不再赘述.

例2设数列{an}满足a1=1,a2=1,an+1=an+an-1(n≥2)，求数列{an}的通项公式.

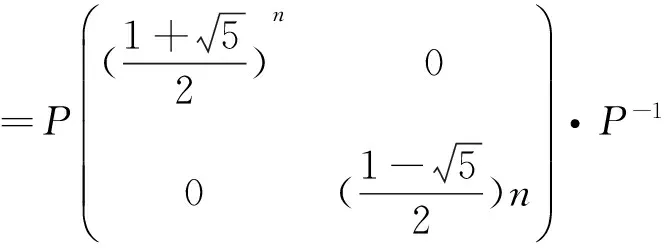
经计算An-1=

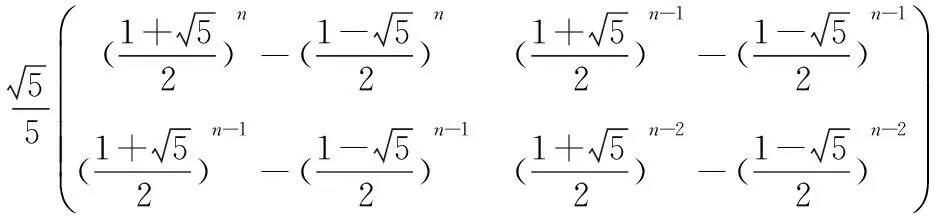
点评：在日常的中学数学教学中,能够用高等数学的思想和方法去处理的中学数学问题很多,张奠宙教授说过,作为一名数学老师,应该具有居高临下的意识,这样才能真正发挥其对中学数学教学的指导作用.