一种提高奇偶交错体积阵处理速度的分解方法*

黄　迪　楼万翔

(杭州应用声学研究所　杭州　310012)



一种提高奇偶交错体积阵处理速度的分解方法*

黄迪楼万翔

(杭州应用声学研究所杭州310012)

针对奇偶交错体积阵无法使用整齐布阵的快速处理方法造成计算量成倍增加的问题，文章详细分析了奇偶交错体积阵的处理过程，提出将奇偶交错体积阵按奇数号阵元和偶数号阵元进行分解，重新组合形成两个新的体积阵，然后分别对两个体积阵使用整齐布阵的快速处理方法，最后对两阵处理结果进行加权组合得最终结果，从而大大提高了奇偶交错体积阵的处理速度。通过仿真数据处理证明该方法的结果与直接计算的结果完全重合，但是处理速度远远大于直接计算的速度。

奇偶交错体积阵; 奇数号阵元; 偶数号阵元

Class Number

1　引言

体积阵可以在三维空间对信号进行空间采样，是当前声纳中最常用的阵型之一。体积阵在布阵时将奇数层阵元和偶数层阵元在水平方向上交错水平阵元间距的一半，或者奇数列阵元和偶数列阵元在垂直方向上交错垂直阵元间距的一半 (如图1所示)，可以使得水平维等效阵元间距是整齐布阵(即每列奇偶阵元在同一垂线上，每行阵元在同一平面上，如图2下面两图所示)的一半，可以在不增加阵元数的基础上，提高基阵的频带处理上限，降低了布阵的经济成本，是当前体积阵的一种常用布阵形式[3～4]。

现在针对整齐布阵的体积阵通常存在快速处理方法[1～2]，可以成倍的提高基阵的处理速度，降低基阵信号处理的经济成本，但是对于奇偶交错的体积阵由于奇数层和偶数层(或者奇数列和偶数列)交错，不适用这些快速处理方法。现有针对奇偶交错体积阵的处理方法都是对每个阵元的数据根据阵元坐标和预成角度逐个进行相位补偿，这样产生的计算量成倍的增加，增加了基阵信号处理的经济成本。在基阵阵元数众多的情况下，一定程度上会抵消奇偶布阵阵元数减少带来的成本优势，为此提出一种针对交错阵的快速处理方法显得非常必要。

本文详细分析了奇偶交错体积阵的波束形成的处理过程，发现将处理结果可以分解成奇数号阵元处理结果和偶数号阵元处理结果加权求和的形式，特别是权系数与阵元位置无关，进而可以将奇偶交错体积阵等效分解为奇数号阵元和偶数号阵元组合成的新的体积阵，新的体积阵是整齐布阵的形式可以采用整齐布阵的快速处理方法，从而大大提高了奇偶交错体积阵的处理速度。

2　算法原理

2.1算法思想

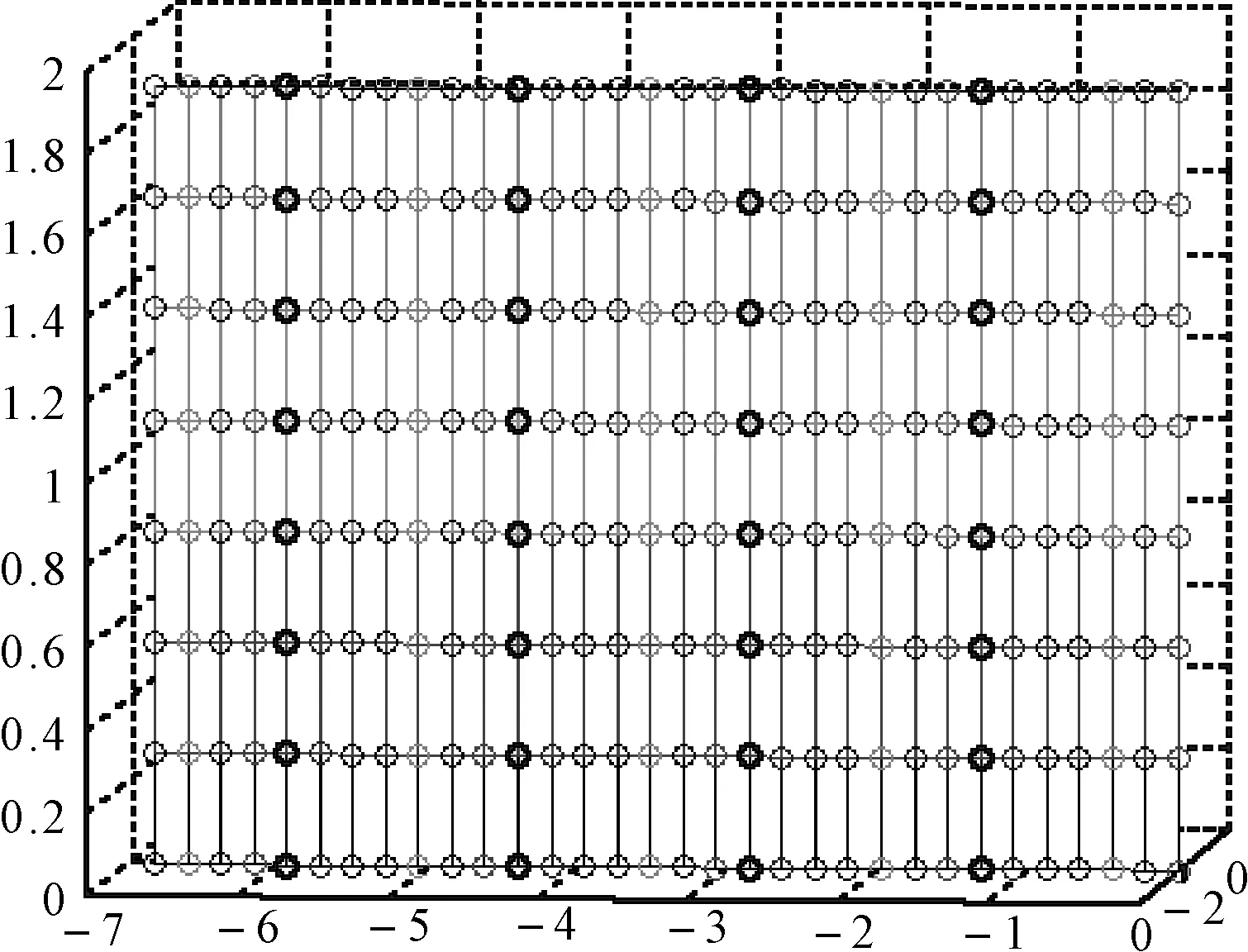
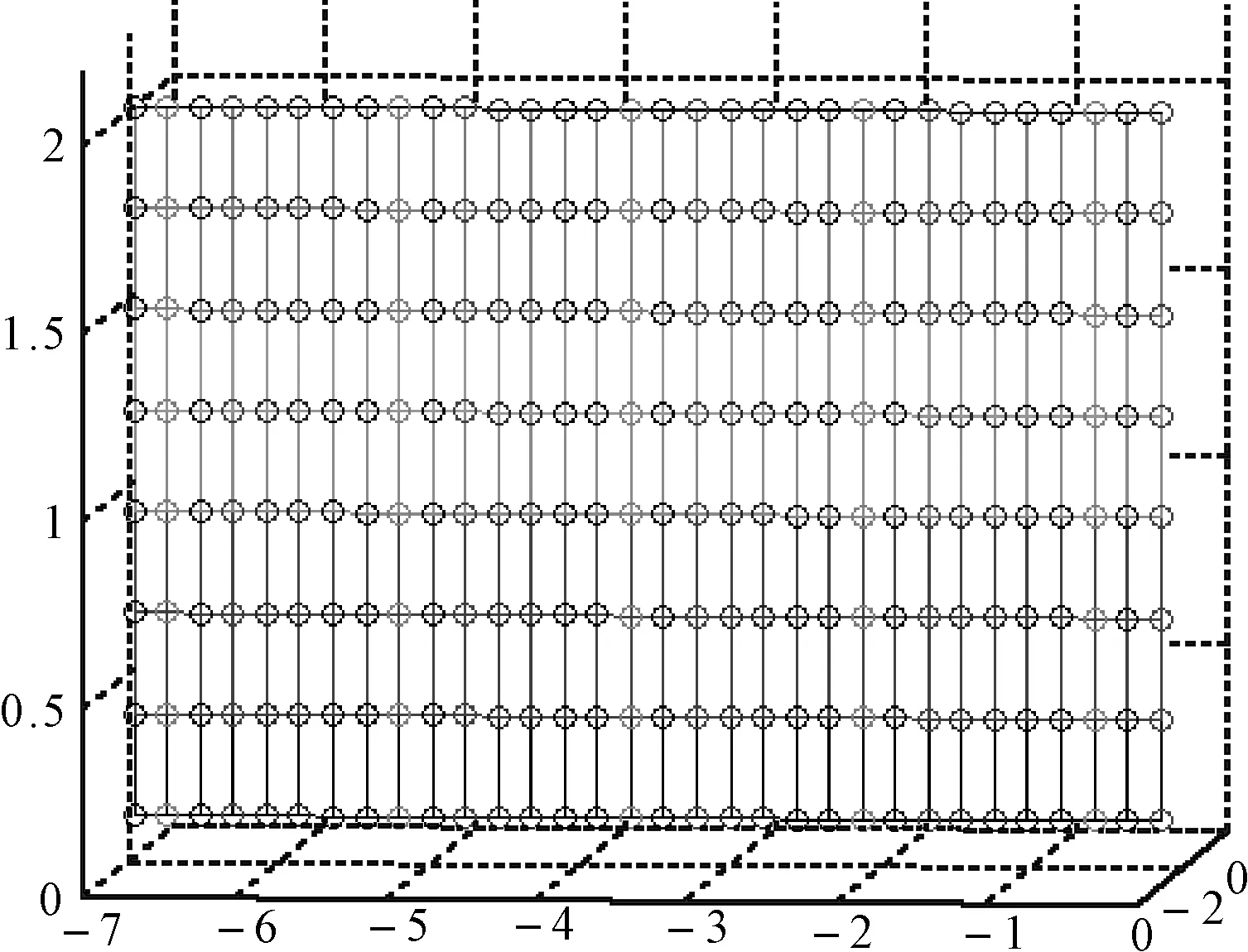
本方法针对奇偶交错的体积阵，将每一列奇数号阵元和偶数号阵元分开，形成两个垂直阵元均在一条直线上(如图2，图3)，垂直阵元间距是原来两倍的新的体积阵，然后采用整齐布阵体积阵的快速处理方法分别对两个新阵进行处理，根据两新阵的相对位置将两阵处理结果进行加权求和，最后得到交错阵的处理结果。

(a)

(b)

(a)

(b)

(c)

(a)

(b)

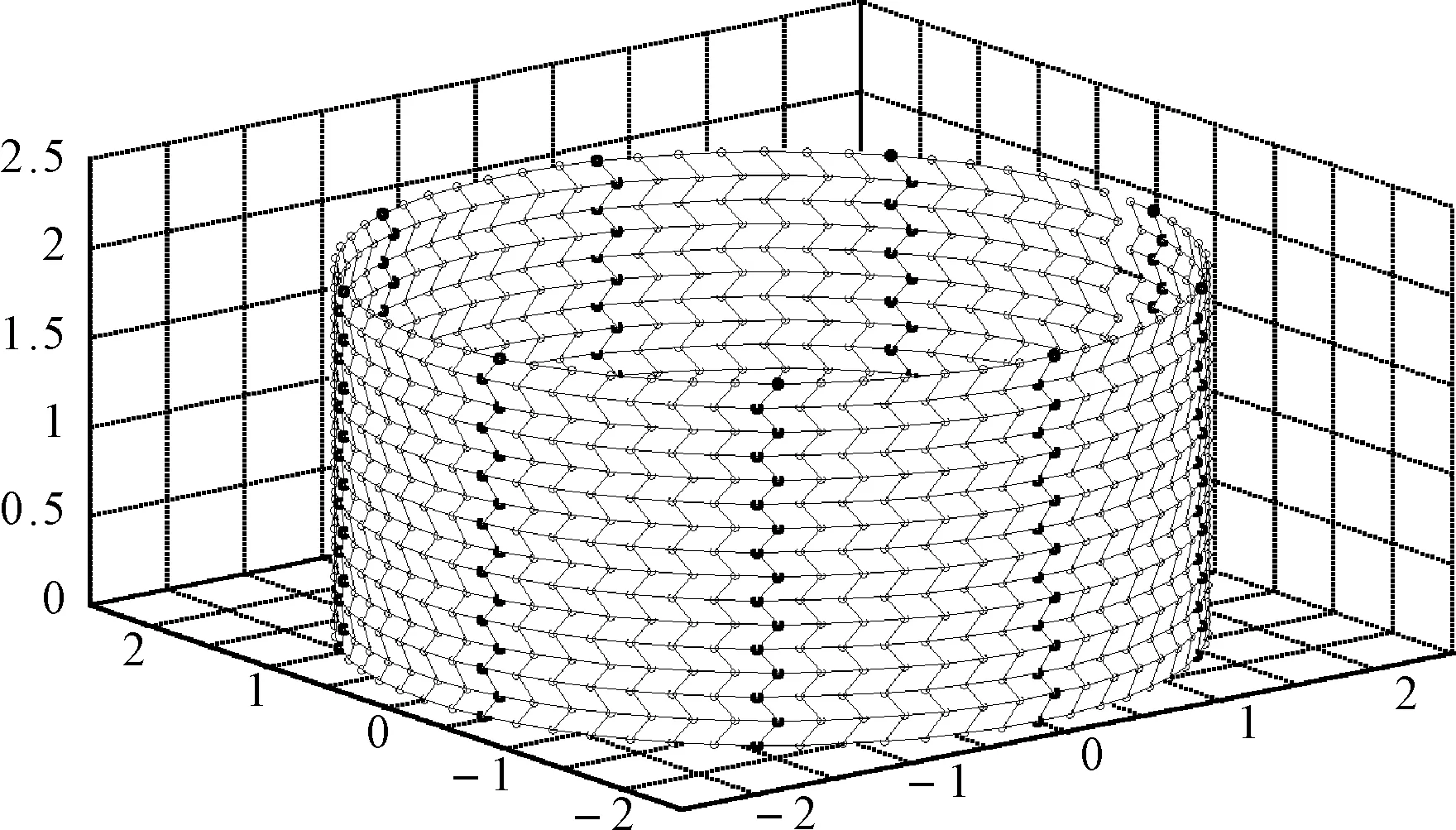
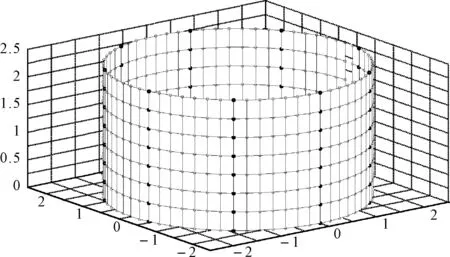
(c)图3　交错圆柱阵(a)变为奇数圆柱阵(b)和偶数圆柱阵(c)分解图

此方法将交错体积阵分解为奇数阵和偶数阵，避免了将交错阵看作整齐阵处理引入的偏差，形成的奇数阵和偶数阵可使用整齐阵的快速处理方法，和根据阵元坐标逐个进行相位补偿的方法相比，大大提高了处理速度。

2.2算法原理

下面以奇偶交错的平面阵为例介绍一下实现原理，(其它体积阵例如圆柱阵原理相同)：

设平面阵(如图2(a)图)共MH层，每层阵元数为ML，阵元间距为d，奇数号阵元和偶数号阵元上下交错。以平面阵底层阵元为xy平面，阵元坐标可以表示为

-R,(mh-1)h}

(1)

其中mh为层数(从1开始)，ml为水平第ml个阵元(从1开始)，R为平面阵距原点的距离，h为层高，%为取余运算。

设信号的入射方位角为θ，俯仰角为φ，则入射的方位矢量为

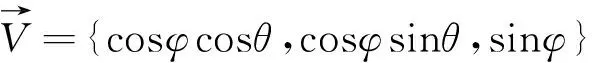
(2)

阵元对应的时延

(3)

这里mh和ml均从0开始。

将交错平面阵分解为奇数阵和偶数阵(如图2)。

体积阵处理都是从波束形成开始的，在某个频点对各阵元补相位求和得：

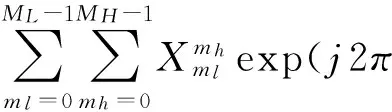
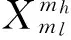
(4)

(5)

(6)

(7)

(8)

从上面的表达式可以看出Ψ与阵元位置无关，Φo,Φi为奇数号阵元和偶数号阵元组成的新的体积阵的结果，所以使用平面阵整齐布阵时的快速算法进行计算。

3　算法流程

1) 根据坐标系确定阵元坐标

2) 将每一列奇数阵元和偶数阵元分开得到奇数阵和偶数阵

3) 使用整齐阵快速算法分别计算奇数阵和偶数阵的结果

4) 计算两阵的加权系数，这里平面阵为

圆柱阵为

其中MR为水平维阵元数，mr为水平维阵元编号，mθ为水平维预成波束角度。

5)将奇数阵和偶数阵结果加权求和得交错阵结果

有的交错体积阵描述时采用水平维奇偶阵元上下交错垂直阵元间距的一半，这和垂直阵元间距是原阵一半，垂直阵元数是原阵两倍，水平阵元间距是原阵两倍，水平阵元数是原阵一般的垂直维交错阵描述的是同一阵型，也可以使用本文的分解方法。

4　算法仿真

设平面阵长7.2m，高2.2m，共8层，每层有64个阵元均匀分布，每层奇数阵元和偶数阵元上下交错。接收的信号为2000Hz的单频信号，采样频率为12kHz，处理的频带宽度为200Hz，信噪比为-20dB。分别比较目标俯仰角为0°，方位角分别为30°、60°、120°、150°快速算法和常规算法的水平维的结果,目标方位角为90度，俯仰角分别为-20°、-10°、10°、20°快速算法和常规算法的垂直维的结果。从两图可以看出快速算法与常规算法的结果完全重合。

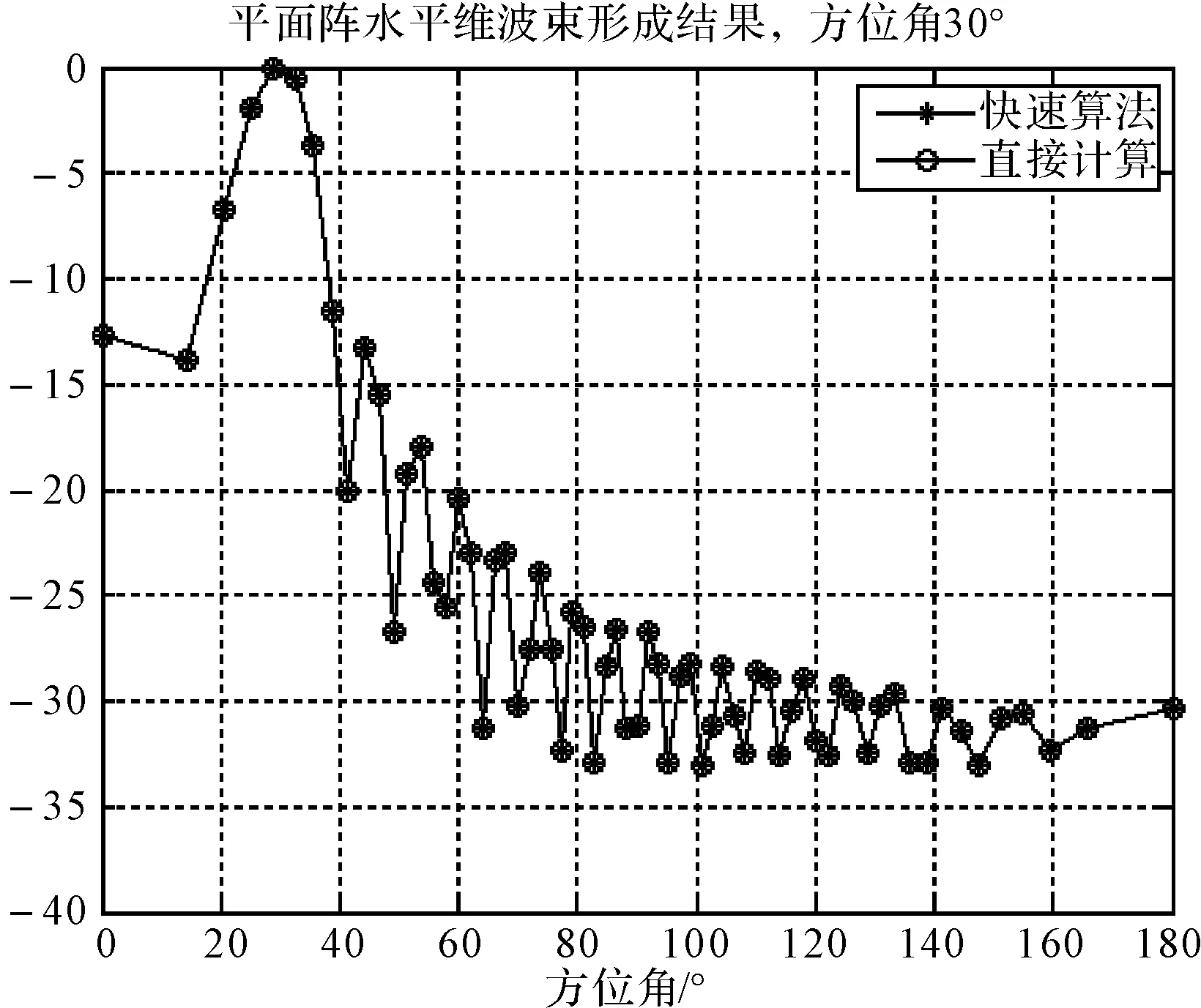
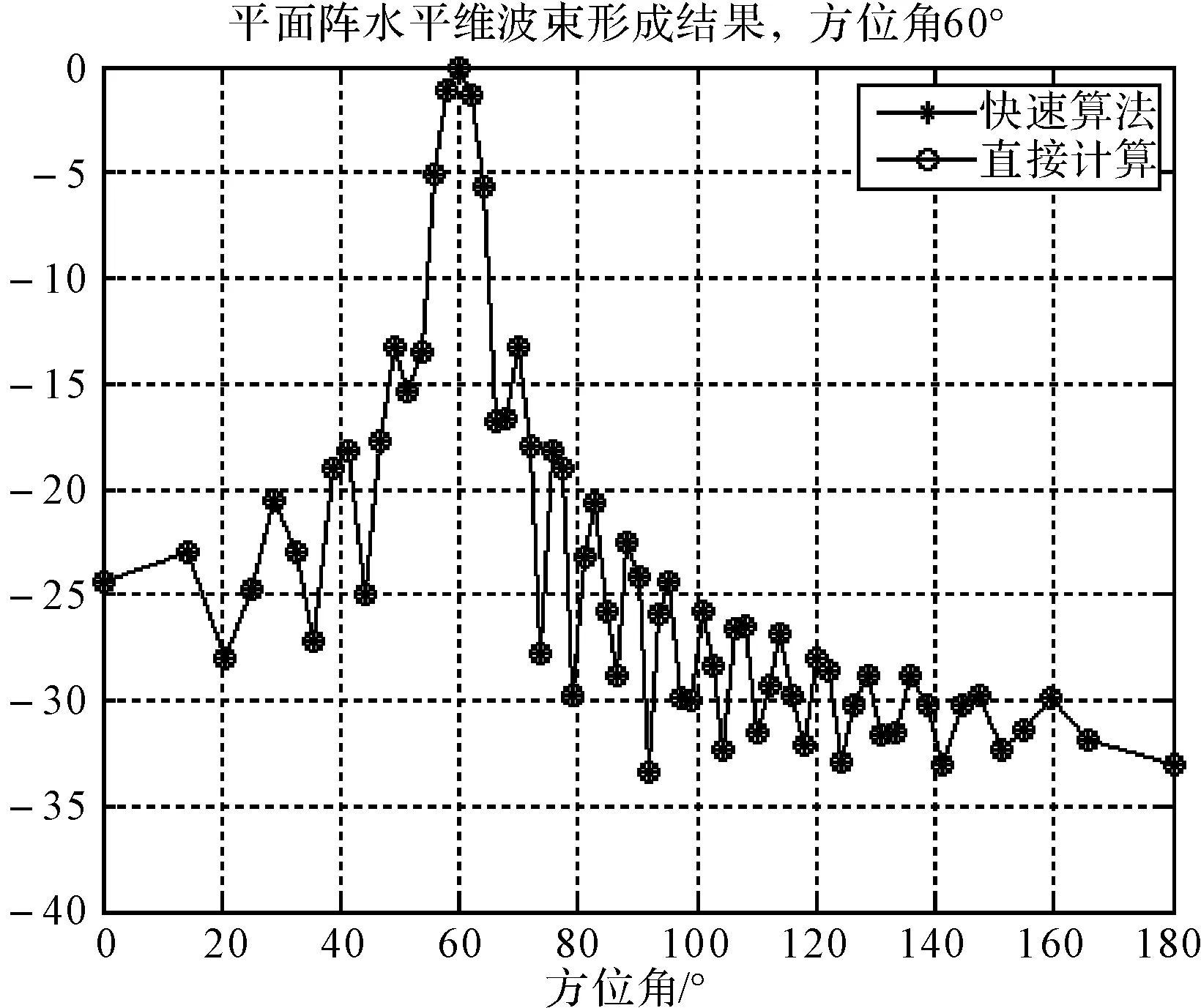
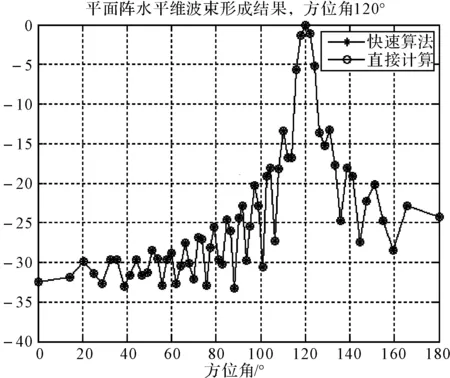
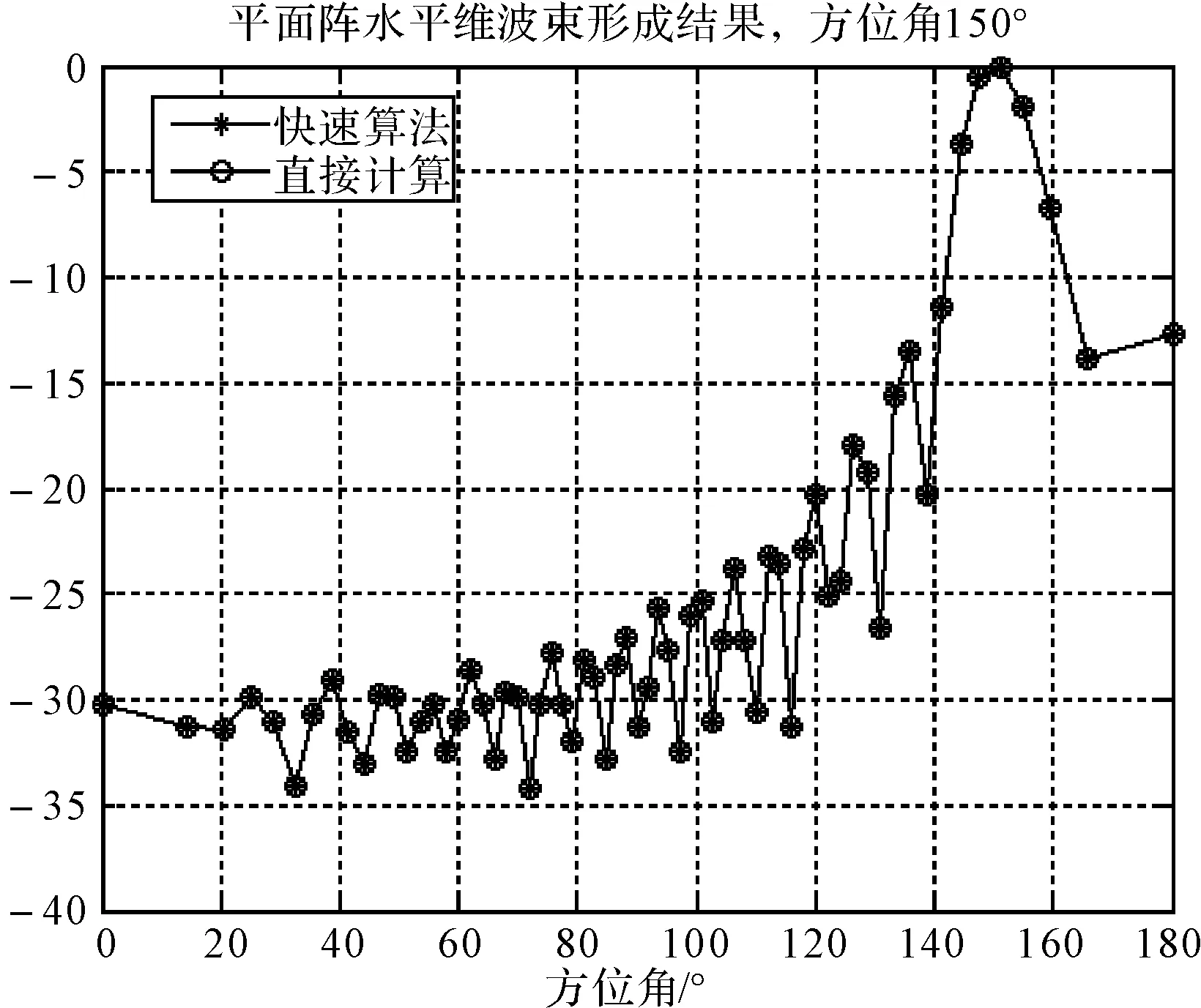
图4　交错平面阵分解后使用快速方法与对直接计算的水平维波束形成结果比较

图5　交错平面阵分解后使用快速方法与直接计算的垂直维波束形成结果比较

表1为不同方位入射时交错平面阵分解后使用快速算法和直接计算的运行时间，从表中可以看出分解后使用快速算法运算速度远远大于分解前直接计算的速度。

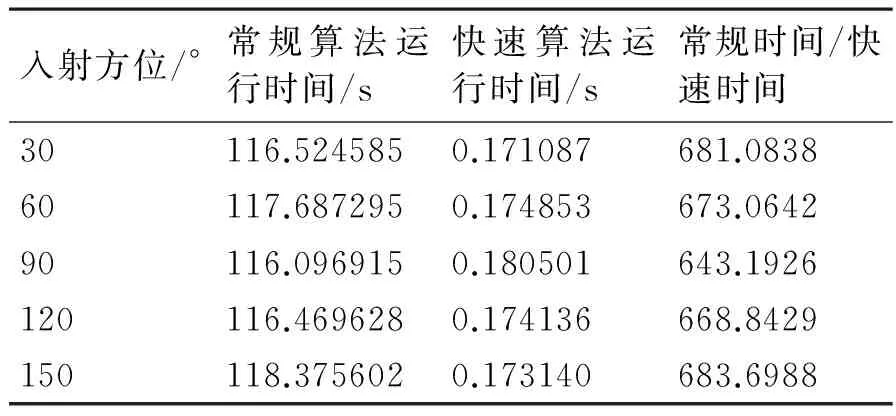
表1　垂直阵元数为16，水平阵元数为32，目标俯仰为0°的分解后使用快速算法和直接计算运行时间

5　结语

本文针对奇偶交错体积阵无法使用整齐布阵的快速处理算法造成计算量成倍增加的问题，分析了奇偶交错体积阵的计算过程，提出将奇数号阵元和偶数号阵元进行分解，重新组合形成两个新的体积阵，然后分别对两个体积阵使用整齐布阵的快速处理方法，最后对两阵处理结果进行组合，从而大大提高了奇偶交错体积阵的处理速度。通过仿真数据处理证明本方法的结果与直接计算的结果完全重叠，但是处理速度远远大于直接计算的速度。

[1] 罗雪松,刘建涛.频域波束形成的FRFT实现[J].声学与电子工程,2005(4):12-18.

[2] 庞振,刘辉涛.调频Z变换实现多阵元线阵频域快速波束形成[J].声学与电子工程,2011(2):21-24.

[3] Josefsson.L, Persson.P.著，肖绍球等译. 共形阵阵列天线理论与应用[M].北京：电子工业出版社,2012:35-47

[4] 王建，郑一农，何子元.阵列天线理论与工程应用[M].北京：电子工业出版社,2015:363-372.

[5] 刘慧霞.天波超视距雷达数据处理若干关键技术研究[D].西安：西北工业大学，2008.

[6] 王增福，潘泉，梁彦，等.天波超视距雷达数据处理算法综述[J].中国电子科学研究院学报，2011,6(5):477-484.

[7] G. W. Pulford. OTHR Multipath Tracking with Uncertain coordinate Registration[J]. IEEE Transactions on Aerospace and Electronic systems,2004,40(1):38-56.

[8] S. B. Colegrov, S. J. DAVEY. PDAF with Multiple Cluster Regions and Target Models[J]. IEEE Transactions on Aerospace and Electronic systems,2003,39(1):110-124.

[9] S. B. Colegrov, S. J. DAVEY, B.Cheung. PDAF Versus PMHT Performance on OTHR Data[C]//Proceedings of the 2003 IEEE Radar Conference Huntsville, AL, United States,2003.

[10] R. P. S. Mahler. Multitarget bayes filtering via first-order multitarget moment[J]. IEEE Transactions on Aerospace and Electronic systems,2003,39(4):1152-1178.

A Decomposition Method To Improve Processing Speed of Odd-even Staggered Volume Array

HUANG DiLOU Wanxiang

(Hangzhou Applied Acoustics Research Institute, Hangzhou310023)

After analyzing the processing of the odd-even staggered volume array in detail, this paper proposes a method to solve the problem that the fast methods of the tidy volume arrays can not be used to deal with the odd-even staggered volume arrays so that the calculation increases greatly. This method decomposes the odd-even staggered volume array to two new arrays, one is composed of the odd elements of the old array, another is composed of the even elements, then the fast methods of the tidy volume arrays are used to calculate the beam-forming of the two new arrays, finally the two results are composed together. This method improves the processing speed greatly. Through dealing with the simulation experimental data, it is proved that the result of this method is the same with the result of common method, but the speed is greatly faster.

odd-even staggered volume array, odd elements, even elements

2016年4月3日,

2016年5月20日

黄迪,男,硕士,工程师,研究方向：声呐总体设计及信号处理。楼万翔,男,硕士,助理工程师,研究方向：声呐总体设计及信号处理。

TN929

10.3969/j.issn.1672-9730.2016.10.035