基于速度匹配的舰载导弹SINS原位标定方法研究*
庞晓楠 王 磊 李向阳
(1.海军潜艇学院 青岛 266000)(2.海军航空工程学院指挥系 烟台 264001)
基于速度匹配的舰载导弹SINS原位标定方法研究*
庞晓楠1王磊2李向阳2
(1.海军潜艇学院青岛266000)(2.海军航空工程学院指挥系烟台264001)
提出了一种基于速度匹配的多种发射装置通用的舰载导弹捷联惯导原位标定方法,分析了标定参数误差对于导航精度的影响,设计了标定方案和标定流程,研究了标定算法,试验结果验证了所提方法的可行性和有效性。
舰载导弹; 速度匹配; SINS; 原位标定方法
Class NumberTN 957.51
1 引言
惯导系统经过长时间的使用和贮存,其惯性器件(陀螺和加速度计)参数如零偏和标度因数都会发生变化,参数变化会惯导系统使用精度下降。造成参数变化的主要因素有[1~2]:
1) 惯性器件内部环境如磁性环境随时间发生变化,造成器件标度因数变化;
2) 惯性器件其结构材料本身的弹性后效、弹性滞后、材料蠕变以及加工过程中的残余应力等造成偏值随时间的变化;
3) 安装惯性器件的结构件变形;
4) 与惯性器件配套的电路板用元器件零件或其他特性发生变化,也会表现为惯性器件的零偏或者标度因数变化。
2 误差分析
惯性器件误差主要包括陀螺常值漂移、陀螺标度因数误差、加速度计常值零偏、加速度计标度因数误差和惯性器件的安装误差等[3~6]。
2.1陀螺常值漂移
1) 水平陀螺常值漂移
水平陀螺的常值漂移εx和εy,引起水平姿态误差角变化:
(1)
其中,变量下标x表示载体侧向,y表示载体纵向,z表示载体垂向。
水平姿态误差角使得水平方向的加速度计算时引入重力加速度g的投影分量,从而造成速度和
位置误差,分别为
(2)
(3)
2) 方位陀螺常值漂移
方位陀螺常值漂移εz,引起的航向姿态误差为
φz(t)=εz×t
(4)
速度误差为
ΔVx(t)≈V·εz·t
(5)
位置误差为
(6)
2.2陀螺标度因数误差
1) 水平陀螺标度因数误差
陀螺标度因数误差主要在角运动中表现出来。假设飞行过程中惯导俯仰角转动Δθ,引起的俯仰角姿态误差:
φx=Δθ×δKgx
(7)
速度和位置误差为:
ΔVy(t)≈g·Δθ·δKgx·t
(8)
(9)
2) 方位陀螺标度因数误差
当载体飞行航向中存在双边角度机动,例如蛇行机动,正负方向投影误差可以相互抵消。而当载体飞行航向存在单边大角度运动时,陀螺标度因数误差将产生航向误差。
假设载体飞行过程中航向转动Δψ,方位陀螺标度因数引起的航向误差为
φz=Δψ·δKgz
(10)
速度误差为
ΔVx(t)≈V·Δψ·δKgz
(11)
位置误差为
ΔSx(t)≈V·Δψ·δKgz·t
(12)
2.3加速度计零偏
加速度计零偏引起的速度和位置误差为
(13)
(14)
2.4加速度计标度因数误差
加速度计标度因数引起的速度和位置误差为
ΔVy(t)=δKay·V
(15)
ΔSy(t)=δKay·V·t
(16)
2.5陀螺安装误差
1) 等效误差
载体没有大的角运动时,陀螺的安装误差等价于陀螺的常值漂移误差。若安装误差变化量为6″,则产生0.0004°/h的等效陀螺漂移,可以忽略不计。
2) 航向角运动投影误差
当导弹存在单边大角度运动时,陀螺安装误差将产生角速度投影误差。假设导弹在平飞过程中航向转动Δψ,安装误差产生俯仰角投影误差和滚动角投影误差。
(1)滚动角误差
φy=Δψ·δKgyz
(17)
速度和位置误差为
ΔVx(t)≈g·Δψ·δKgyz·t
(18)
(19)
(2)俯仰角误差
φx=Δψ·δKgxz
(20)
(21)
3) 俯仰角运动投影误差
导弹垂直发射转平飞过程中俯仰角运动转动Δθ,安装误差产生滚动角投影误差和航向角投影误差。
(1)滚动角误差
φy=Δθ·δKgyx
(22)
速度和位置误差为
ΔVx(t)≈g·Δθ·δKgyx·t
(23)
(24)
(2)航向角误差为
φz=Δθ·δKgzx
(25)
速度和位置误差为
宋明理学包含两大流派——“程朱理学”和“陆王心学”,这两大流派代表人物的观点中有相同之处也有不同之处,学生难以区分,因此教师可提供以下几则材料帮助学生分析理解“程朱理学”与“陆王心学”的异同。
ΔVx(t)≈V·Δθ·δKgzx
(26)
ΔSx(t)≈V·Δθ·δKgzx·t
(27)
2.6加速度计安装误差
1) 等效误差
当载体匀速飞行时,加速度计的安装误差等效于加速度计常值零偏。
速度和位置误差
(28)
(29)
2) 投影误差
当载体加速飞行时,纵向存在线加速度过程,安装误差将在侧向产生加速度投影误差:
ΔVx(t)=δKaxy·V
(30)
ΔSx(t)=δKaxy·V·t
(31)
2.7误差分析小结
假设惯导系统参数变化如下:陀螺常值漂移变化0.1°/h,陀螺标度因数变化200ppm,加速度计零偏变化0.1mg,加速度计标度因数变化200ppm,陀螺和加速度计的安装误差变化6″。
惯性器件误差造成的导航误差见表1。
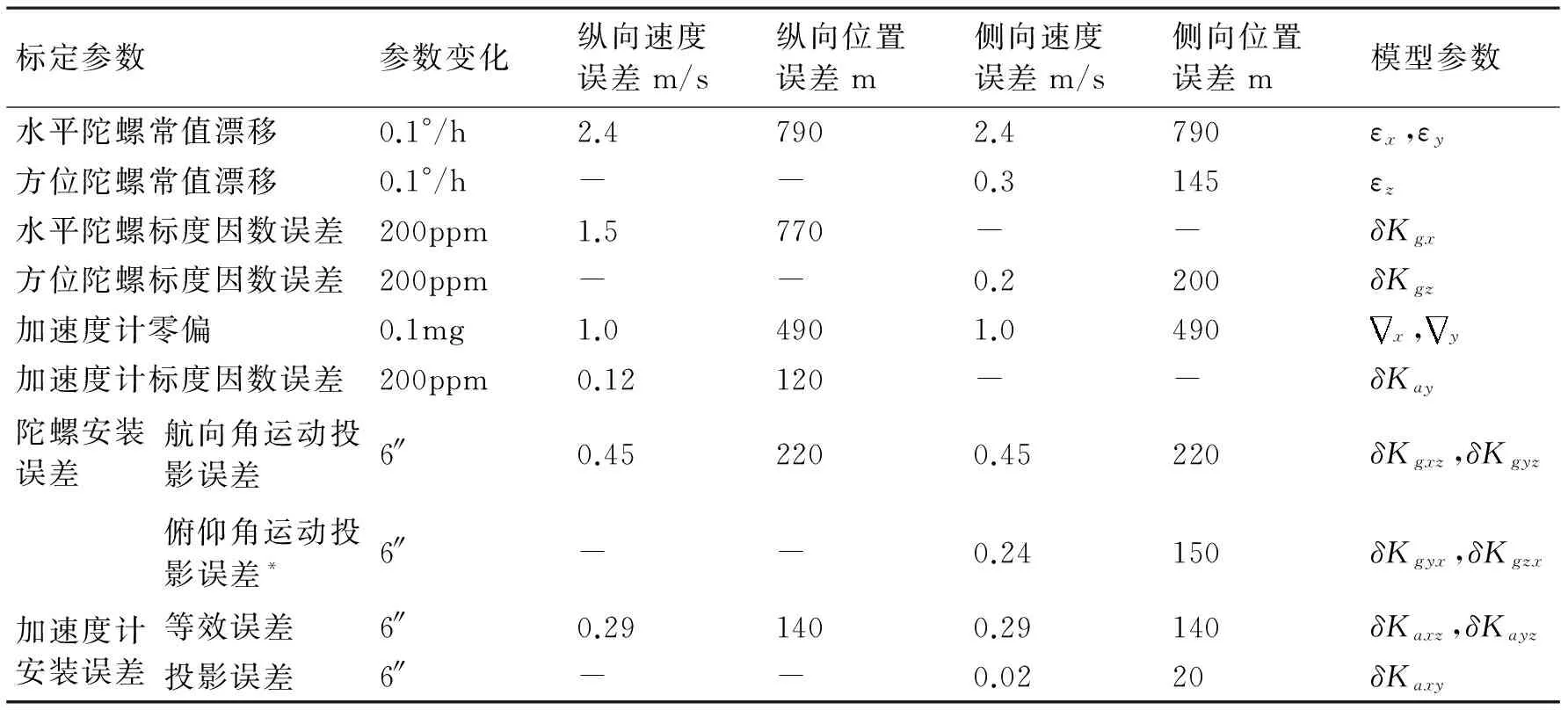
表1 导航误差
3 基于速度匹配的原位标定方法
3.1标定方案
原位标定技术方案原理如图1所示。
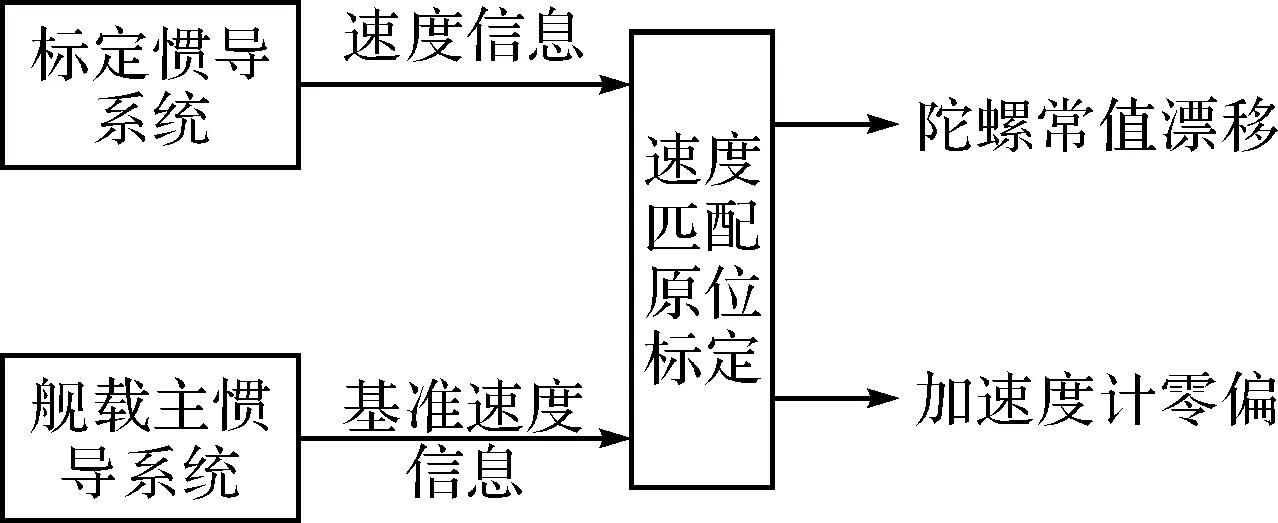
图1 原位标定技术方案原理
3.2标定方案流程
标定流程如图2所示。
3.3标定误差模型
状态变量选取15维状态参数,包括:经度误差、纬度误差、高度误差,东、北、天向的速度误差,东、北、天向姿态误差,三个轴向的陀螺漂移和加速度计零偏:

(32)
1) 状态方程
状态方程由惯导系统的位置、速度误差方程和姿态误差方程组成:
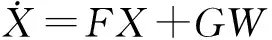
(33)
其中,G表示系统噪声矩阵,W表示系统噪声。

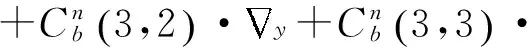
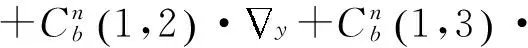
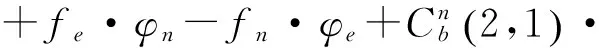
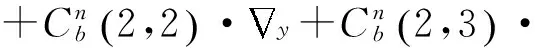

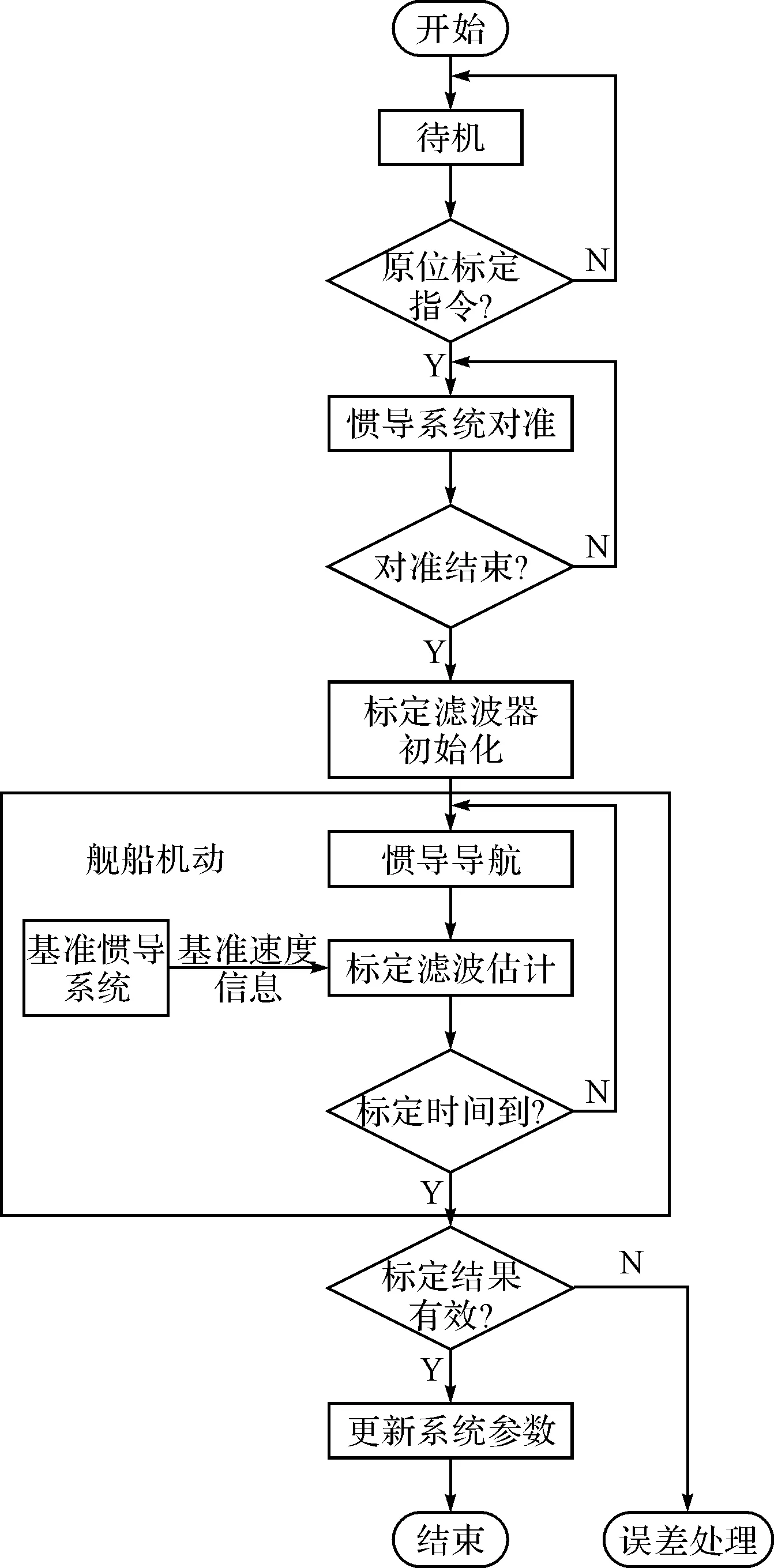
图2 标定方案流程
2) 量测方程
Z=HX+R
观测量Z是标定惯导系统的速度与基准惯导系统速度之差,计算公式如下:
(34)
其中,Vme,Vmn,Vmu是基准惯导速度。
3.4可观性分析

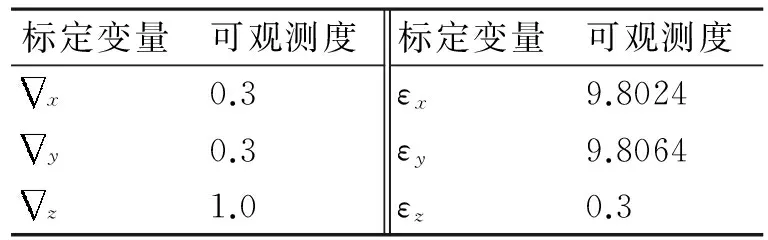
表2 复合运动条件下标定变量的可观测度
可以看出,在复合运动条件下,标定参数全部可观测,而且可观测度较好。
4 杆臂效应补偿
杆臂效应误差与基准惯导和标定惯导的安装位置、舰船的航行状态有关,图3给出了杆臂效应的示意图。
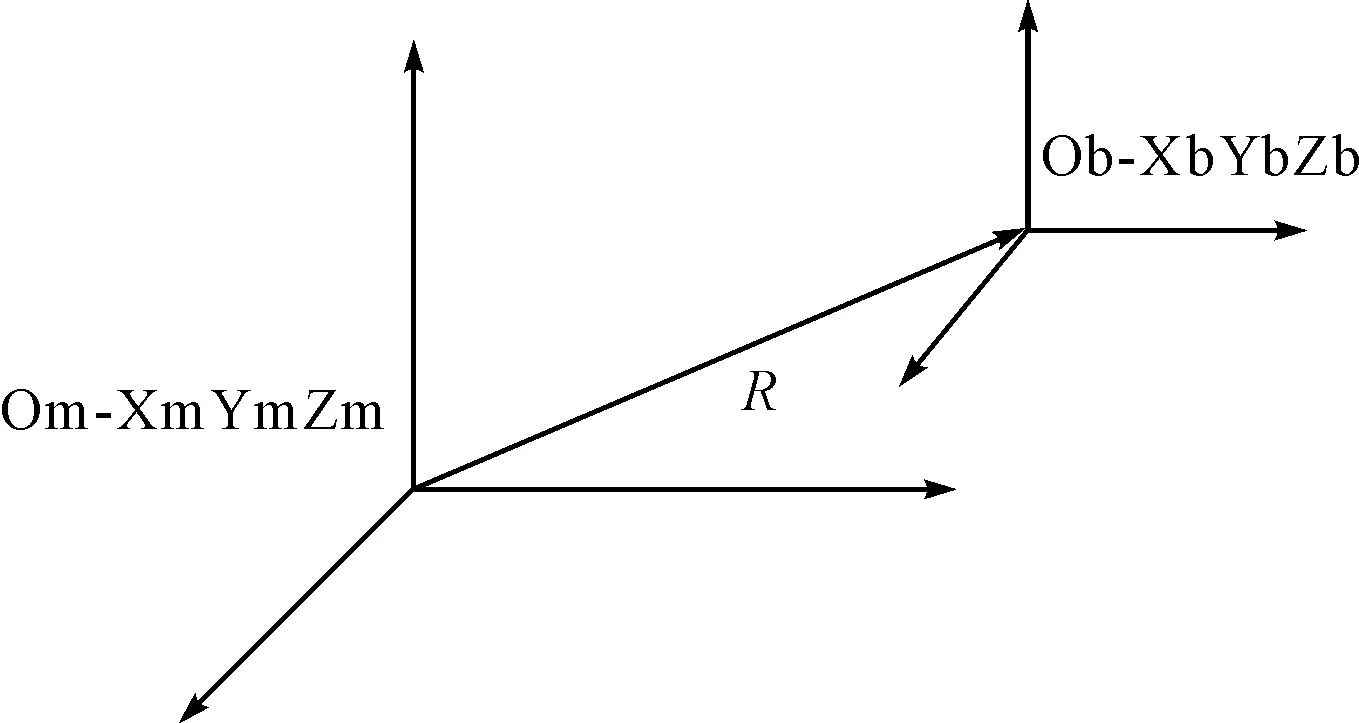
图3 杆臂效应示意图
对杆臂效应的补偿主要有滤波估计补偿法、低通滤波方法和计算补偿法三种方法[7~8]。
这里采用杆臂速度误差计算补偿方法来减小杆臂效应的影响,从而提高标定精度。杆臂速度可由下式计算得到:
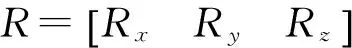
因此,式(4)~式(34)描述的速度误差观测量计算公式修正为
Z=Vb-Vm-VR
(36)
5 仿真验证
数据设定:纬度φ=30°,舰船初始航向角45°、俯仰角0°、滚动角0°,速度20m/s。标定过程中舰船机动过程,线加速运动是北向和东向的线加速度为0.05G;角运动是航向角半圆型机动(单边S型机动),变化幅值45°,航向角变化公式为
(37)
航向角变化曲线如图4所示。
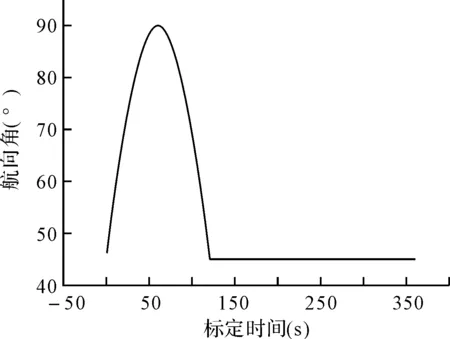
图4 航向角变化曲线
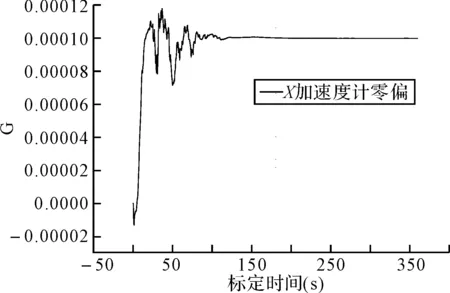
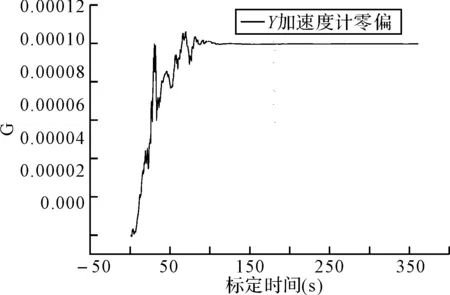
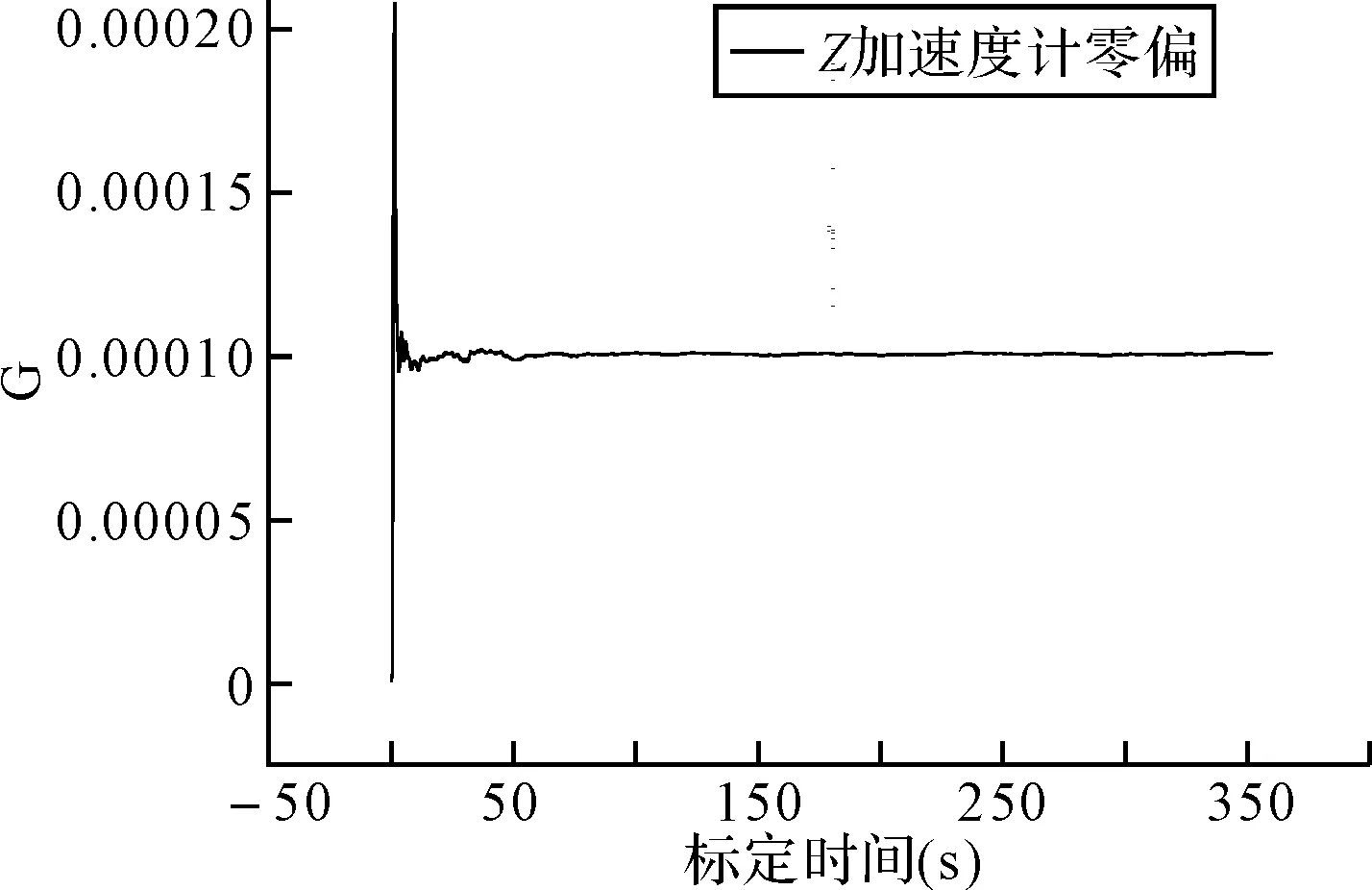
惯性器件误差设定:X,Y,Z陀螺常值漂移为-0.01°/h,X,Y,Z加速度计零偏为0.1mG。标定滤波周期为1s。仿真结果图5所示。
6 结语
本文在分析标定参数误差对于导航精度影响的基础上,设计了标定方案和标定流程,研究了标定算法,提出了一种基于速度匹配的多种发射装置通用的舰载导弹捷联惯导原位标定方法,并通过仿真验证了所提方法的可行性和有效性。
[1] 袁信,俞济祥,陈哲.导航系统[M].北京:航空工业出版社,1993.
[2] 孙昌跃,王司,邓正隆.舰载武器惯导系统对准综述[J].中国惯性技术学报,2005,13(4):81-88.
[3] 李蓓,高伟,王嘉男,等.传递对准中杆臂效应误差的补偿研究[J].弹箭与制导学报,2008(6):49-52.
[4] 房建成,周锐,祝世平.捷联惯导系统动基座对准的可观测性分析[J].北京航空航天大学学报,1999,25(1):714-719.
[5] Fang J C, Wan D J. A fast initial alignment method for strapdown inertial navigation system on stationary base[J]. IEEE Transactions on Aerospace and Electronic Systems,1996,32(4):1501-1505.
[6] Geshen-Meskin D, Bar-Itzhack I Y. Observability analysis of piece-wise constant systems-part I: Theory [J]. IEEE Transactions on Aerospace and Electronic systems,1992,28(4):1056-1067.
[7] 刘毅,刘志俭.捷联惯性导航系统传递对准技术研究现状及发展趋势[J],航天控制,2004(10):51-55.
[8] 李蓓,高伟,王嘉男,等.传递对准中杆臂效应误差的补偿研究[J].弹箭与制导学报,2008(6):49-52.
[9] 房建成,周锐,祝世平.捷联惯导系统动基座对准的可观测性分析[J].北京航空航天大学学报,1999,25(1):714-719.
[10] 胡鑫,韩崇伟,李伟,等.基于四位置转位法实现激光捷联惯性测量组合标定[J].科学技术与工程,2010,10(8):2034-2038.
Research for In-situ Calibration Method of Ship-launched Missile Strapdown Inertial Navigation System Based on Velocity Matching
PANG Xiaonan1WANG Lei2LI Xiangyang2
(1. PLA Navy Submarine Academy, Qingdao266000)(2. Department of Command, Naval Aeronautical and Astronautical University, Yantai264001)
An all types of missile launcher shared and velocity matching based shipboard missile based in-situ calibration technology is proposed. The SINS parameter error influence on the navigation accuracy is discussed, and the calibration scheme and procedure are designed. The simulation results show the feasibility and effectiveness of the proposed approach.
ship-launched missile, velocity matching, SINS, In-situ calibration
2016年4月1日,
2016年5月20日
庞晓楠,男,讲师,研究方向:导航制导与控制。王磊,男,博士,讲师,研究方向:海军兵种作战运用研究,航空兵作战仿真模型。李向阳,男,博士研究生,研究方向:海军兵种作战运用研究。
TN 957.51
10.3969/j.issn.1672-9730.2016.10.012

