适应性预期条件下的双边平台动态最优价格研究

邹 佳，　郭立宏，　张 伟

(西安理工大学 经济管理学院，陕西 西安 710048)



适应性预期条件下的双边平台动态最优价格研究

邹 佳，郭立宏，张 伟

(西安理工大学 经济管理学院，陕西 西安 710048)

本文研究了当市场两边的用户序贯加入时，在先加入一边的用户对后加入一边的用户的数量形成适应性预期的条件下，双边平台的动态最优价格。本文建立了适应性预期的双边市场最优控制模型，在垄断和双寡头两种市场结构中分别使用欧拉方程和拉格朗日乘子法求解出了两种不同表现形式的最优价格序列，前者表现为任意一期最优价格与以往最优价格之间的关系，后者表现为从初始期到终止期的最优价格的完整序列，分别适用于解决平台在以往最优价格已知或以往最优价格未知但终止时间既定这两种情况下的定价问题。最终根据后一种价格序列进行了数值仿真。

序贯加入；适应性预期；最优控制模型；最优价格序列

1　引言

在双边市场中，市场一边的用户使用平台所获得的价值取决于市场另一边的用户数量，正是因为这种组间外部性的存在，使双边市场任意一边的需求都取决于另一边的需求[1,2]。但是当市场的两边并不是同一时间加入平台时，先加入一方的用户就无法观察到后加入一方的实际需求。例如零售平台和B2C电子商务平台通常会先引入卖家，然后才会有买家加入，在决定是否加入平台时，买家可以通过直接观察卖家的实际数量进行决策，但是卖家却无法观察到买家的实际数量，同样的情况也会出现在电脑操作系统、电子游戏以及广告等不同类别的双边市场中。在这种情况下，先加入一方用户只能依据对另一方用户数量的预期进行决策。但是当先加入一方的用户所获得的信息并不充分时，例如无法观察到平台在市场另一边的价格或者无法准确判断市场另一边的价格对该边需求的影响时，就不能使自己的需求预期对价格的反应与实际的需求反应保持一致[3]。

对于缺乏信息的用户来说，适应性预期(adaptive expectation)是一种合理的假设，因为采用适应性预期的用户只需要通过观察市场另一边以往的实际需求和预期需求就可以形成新预期并不断自我修正，相比较使预期需求与实际需求总是保持一致所需的信息，适应性预期所需的信息通常更容易获得。适应性预期的概念最早由Cagan[4]提出，用于解释人们对通货膨胀的预期，随后Phelps[5]和Friedman[6]使用适应性预期描述了Phillips曲线。在通货膨胀、同业拆借市场、股票价格和农产品市场等多个方面，都有研究证实了适应性预期的存在[7～15]。

本文将离散时间形式的适应性预期模型[4,5]引入到双边市场的研究中，用于研究当市场两边序贯加入时，双边平台在先加入一方用户缺乏信息和非理性条件下的动态最优价格。本文假定平台能够对价格进行动态调整，先加入一方的用户会根据以往的实际需求和预期需求而形成新的预期，预期和价格会相互影响而不断发生变化，在此条件下对平台的最优价格进行了研究。

与现有的双边市场研究相比，本文的创新点如下：(1)将适应性预期用于双边市场的研究中。现有研究对预期的假设分为三种：第一种假定用户拥有充足的信息，预期能够积极地响应平台价格的变动，也就是预期需求与实际需求总是能够保持一致，这种预期被称为响应性预期(responsive expectation)[3]，大多数研究都采用这种假设[6～22]。

其余两种是消极性预期(passive expectation)[23]和谨慎性预期(wary expectation)，它们都假定用户缺乏信息，前者指用户对市场另一边的需求形成一个固定的预期而不随价格发生变化，后者指用户通过观察本方价格而预测平台在另一方的最优价格及最优需求，并将这种最优需求作为预期[3]。Gabszewicz和Wauthy[23]首次将消极性预期用于双边市场，研究了消极性预期条件下垄断市场和具有纵向差异的双寡头市场的产出，并与响应性预期的情况进行了比较；Hagiu和Halaburda[3]将Gabszewicz和Wauthy[23]的研究推进了一步，系统地研究了用户在不同信息水平下所形成的预期对垄断市场和具有横向差异的双寡头市场的均衡价格和利润的影响，作者除了对纯粹的响应性预期和消极性预期进行了比较之外，还比较了二者的混合模式并新引入了谨慎性预期。

适应性预期的特点是用户能够通过观察过去的经验而形成当下的预期，因此在动态过程中当用户既缺乏信息又不会保持预期固定不变，而且还非理性时，适应性预期是更加符合现实的假设。

(2)使用动态模型刻画了价格和预期的变化过程。双边市场的静态均衡研究只能对达到稳定状态的价格进行研究，而且通过假定预期一定会实现而完全省略了在形成均衡的过程中预期和价格的变化过程[1～3,16～23]。本文所建立的动态模型以参与者每个时期的行为作为基础，考虑到了各个参与者决策的变动过程，因此对解决短期的或非均衡状态的平台定价问题会更加有效。

现有的双边市场动态研究并没有重点对用户预期问题进行过分析，也没有对预期类型提出过明确的假设，例如：Damiano和Lam[24]对存在使动态配对市场趋向稳定的配对策略的一般性条件的探讨，Satterthwaite和Shneyerov[25]，Shneyerov和Wong[26]对商品保留价格和成本方面信息不对称的配对交易市场的研究，Kim和Tse[27]，Kang和Downing[28]对在位者和进入者之间竞争的研究，Koh和Fichman[29]在买方用户多归属条件下对买方用户对相互竞争的两个平台中某个特定平台的偏好与该平台的买卖交易量之间的关系的研究等。这部分研究都没有考虑当一边用户无法积极响应另一边用户的行为时的情况，因此本文与这部分研究的主要区别在于：在一边用户无法积极响应另一边用户行为的假定下对平台的动态价格进行研究，着重考虑预期对平台价格的影响，并且能够以解析的形式求解出价格、预期需求、实际需求和利润的动态变化过程。

(3)考虑了市场两边的用户序贯决策的情况。当市场两边的用户并不是同一时间加入平台，且平台按照两边加入的顺序序贯定价时，两边用户的决策就是序贯的。因为在行动时先加入一方用户无法观察到后加入一方的价格及需求反应，而后加入一方用户则可以观察到先加入一方的价格和需求。在动态过程中这是一种合理的假设，因为平台的价格和需求有可能随时间发生变化，先加入一方无法根据以往的经验来消除决策时所面临的不确定性，而无论对方的需求如何变化，后加入一方在决策时都可以观察到一个确定的结果。但现有的动态和静态研究都没有考虑过这种情况[1～3,16～29]。

2　基本假设

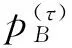
π(τ)是平台在第τ期的利润。为了简化模型假定平台没有成本，利润函数为

(1)

3　垄断市场

3.1最优控制模型

在每一个时期内平台都会和用户进行一轮博弈，博弈顺序为：(1)平台决定卖方价格；(2)卖方用户观察到平台卖方价格后决定是否使用平台；(3)平台观察到卖方用户数量后决定买方价格；(4)买方用户观察到卖方用户数量以及买方价格后决定是否使用平台。通过倒序求解后三阶段博弈可以将买方最优价格、平台最优需求和最优利润变为卖方最优价格的函数，由于卖方价格取决于用户的预期需求，而预期需求会与实际需求相互影响而不断发生变化，因此卖方最优价格要通过建立以预期需求作为状态变量的最优控制模型来求解。本小节将在求解后三阶段博弈的基础上建立最优控制模型，而随后的两个小节则对最优控制模型进行求解。

(2)

π(τ)为凹函数的二阶条件为αB<2。

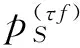
(3)

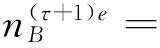
(4)

3.2欧拉方程解

欧拉方程可以表示出动态最优条件下不同时期的控制变量之间的关系，因此通过求解欧拉方程可以获得平台当期最优价格与以往最优价格之间的关系，当平台能够获得有关以往最优价格的信息时，就可以按照这种方法制定价格。

将(2)式代入该式进行计算并结合上一小节的内容，可得出平台任意一个时期的最优价格应满足的条件为

(5)

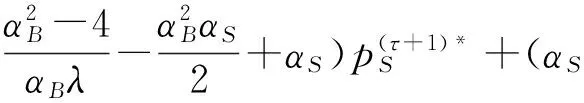
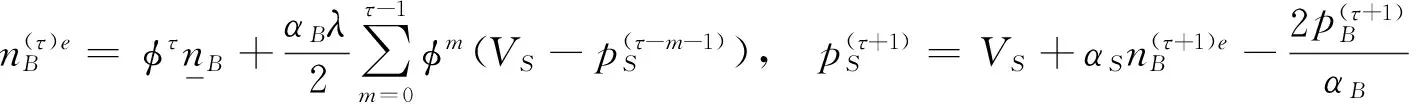
由(5)式可以看出，垄断平台任意一期的买方和卖方的最优价格都取决于上一期的买方或卖方的最优价格和买方需求的预期，而任意一期买方需求的预期则取决于买方或卖方以往所有时期的最优价格，因此在初始预期已知的条件下，当平台能够获得买卖两方中任何一方以往最优价格的所有信息时，便可以按照这种方法制定当期和随后无限时期的价格。

3.3拉格朗日乘子法解

当平台无法获得有关以往价格的信息时就无法使用(5)式所示的方法定价，例如一个提供新型服务的初创平台既没有自己的历史信息也无法参考其他平台的价格。因此本小节使用拉格朗日乘子法求解模型，获得在终止时间既定条件下的完整的最优价格序列，作为平台在该情况下的定价方法。

(6)

4　双寡头市场

4.1最优控制模型

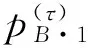
在最优状态下平台在买方的最优价格和市场份额为

(7)

平台1在第τ期的利润为

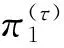
(8)

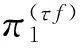
(9)

(10)

4.2欧拉方程解

(11)

与垄断的情况不同，双寡头平台在买方的最优价格仅与差异化水平相关，而任意一个时期的卖方最优价格仅取决于上一个时期的卖方最优价格。在初始预期已知的条件下，通过(7)式和(11)式，平台可以根据以往任意一期的卖方最优价格制定当期及随后无限时期的价格。

4.3拉格朗日乘子法解

(12)

5　数值仿真

6　结论

本文在用户采用适应性预期的条件下建立了双边市场的最优控制模型，在垄断和双寡头两种市场结构中，分别通过欧拉方程和拉格朗日乘子法求解出两种不同表现形式的最优价格序列，对平台的动态最优价格进行了研究，最终得出以下结论：

(1)在垄断市场中，在初始预期已知的条件下，平台任意一期的买方和卖方的最优价格都可以表示为买卖两方中任何一方以往所有时期的最优价格的函数或者时间的函数，二者分别由文中的(5)式和(6)式给出。当任何一方以往所有时期的最优价格都已知时，平台可以按照(5)式制定当期和随后无限时期的买方和卖方价格；当以往价格未知但终止时间既定时，平台可以按照(6)式制定自初始期到终止期的买方和卖方价格。

(2)在对称的双寡头市场中，平台的买方最优价格等于平台之间的差异化程度而与时间无关；在初始预期已知的条件下，任意一期的卖方最优价格可以表示为上一期卖方最优价格的函数或者时间的函数，二者分别由文中的(11)式和(12)式给出。当以往任意一期的卖方最优价格已知时，平台可以按照(11)式制定当期和随后无限时期的卖方价格；与垄断的情况相同，当以往价格未知但终止时间既定时，平台可以按照(12)式制定自初始期到终止期的卖方价格。

本文的研究还可以在预期类型和市场结构两方面进行拓展。通过对模型中的状态方程进行调整，可以将研究拓展到其他类型预期的市场；对双寡头市场的研究可以通过Salop环[32,33]的方法拓展到一般性的差异化多寡头市场，同时也可以稍加改变就拓展到两边都具有差异化且单归属的寡头市场。

本文的主要不足在于没有考虑用户采用不同预期时的情况。在今后的研究中，作者将对适应性预期条件下双边市场趋于稳态的一般性条件进行探讨，并且还要以某个具体的双边市场为例对用户预期的类型进行实证检验。

[1] Rochet J C, Tirole J. Platform competition in two-sided markets[J]. Journal of the European Economic Association, 2003, 1(4): 990-1029.

[2] Rochet J C, Tirole J. Two-sided markets: a progress report[J]. The RAND Journal of Economics, 2006, 37(3): 645- 667.

[3] Hagiu A, Halaburda H. Information and two-sided platform profits[J]. International Journal of Industrial Organization, 2014, 34(1): 25-35.

[4] Cagan P. The monetary dynamics of hyperinflation[A]. In Friedman M, ed. Studies in the Quantity Theory of Money[C]. Chicago: University of Chicago Press, 1956. 25-117.

[5] Phelps E S. Phillips curves, expectations of inflation and optimal unemployment over time[J]. Economica, 1967, 34(3): 254-281.

[6] Friedman M. The role of monetary policy[J]. American Economic Review, 1968, 58(1): 1-17.

[7] 杨继生.通胀预期、流动性过剩与中国通货膨胀的动态性质[J].经济研究，2009，(1)：106-117.

[8] 李永宁,赵钧,黄明皓.经济学家的通货膨胀预期：理论与实证[J].经济理论与经济管理，2010，(4)：25-32.

[9] 于光耀，徐娜.中国通货膨胀预期：理性还是适应性[J].财经科学，2011，(11)：1-10.

[10] Chow G C. Rational versus adaptive expectations in present value models[J]. Review of Economics and Statistics, 1989, 71(3): 376-384.

[11] 王曦，陈淼.理性预期还是适应性预期：基于同业拆借市场的检验[J].学术研究，2013，(1)：75- 81.

[12] Chow G C, Fan Z Z, Hu J Y. Shanghai stock prices as determined by the present-value model[J]. Journal of Comparative Economics, 1999, 27(3): 553-561.

[13] 危慧惠.基于红利贴现的适应性预期股价决定模型研究[J].数学的实践与认识，2005，35(8)：36- 40.

[14] Nerlove M. The dynamics of supply: retrospect and prospect[J]. American Journal of Agricultural Economics, 1979, 61(5): 874- 888.

[15] 陈飞，范庆泉，高铁梅.农业政策、粮食产量与粮食生产调整能力[J].经济研究，2010，(11)：101-114.

[16] Caillaud B, Jullien B. Chicken & egg: competition among intermediation service providers[J]. RAND Journal of Economics, 2003, 34(2): 309-328.

[17] Armstrong M. Competition in two-sided markets[J]. The RAND Journal of Economics, 2006, 37(3): 668- 691.

[18] Armstrong M, Wright J. Two-sided markets, competitive bottlenecks and exclusive contracts[J]. Economic Theory, 2007, 32(2): 353-380.

[19] Hagiu A. Two-sided platforms: product variety and pricing structures[J]. Journal of Economics & Management Strategy, 2009, 18(4): 1011-1043.

[20] Weyl E G. A price theory of multi-sided platforms[J]. American Economic Review, 2010, 100(4): 1642-1672.

[21] Bedre-Defolie O, Calvano E. Pricing payment cards[J]. American Economic Journal: Microeconomics, 2013, 5(3): 206-231.

[22] Reisinger M. Two-part tariff competition between two-sided platforms[J]. European Economic Review, 2014, 68: 168-180.

[23] Gabszewicz J J, Wauthy X Y. Vertical product differentiation and two-sided markets[J]. Economics Letters, 2014, 123(1): 58- 61.

[24] Damiano E, Lam R. Stability in dynamic matching markets[J]. Games and Economic Behavior, 2005, 52(1): 34-53.

[25] Satterthwaite M, Shneyerov A. Convergence to perfect competition of a dynamic matching and bargaining market with two-sided incomplete information and exogenous exit rate[J]. Games and Economic Behavior, 2008, 63(2): 435- 467.

[26] Shneyerov A, Wong A C L. Bilateral matching and bargaining with private information[J]. Games and Economic Behavior, 2010, 68(2): 748-762.

[27] Kim K, Tse E. Dynamic competition strategy for online knowledge-sharing platforms[J]. International Journal of Electronic Commerce, 2011, 16(1): 41-76.

[28] Kang J S, Downing S. Keystone effect on entry into two-sided markets: an analysis of the market entry of WiMAX[J]. Technological Forecasting & Social Change, 2015, 94: 170-186.

[29] Koh T K, Fichman M. Multi-homing users’ preferences for two-sided exchange networks[J]. MIS Quarterly, 2014, 38(4): 977-996.

[30] 扬奎斯特,萨金特.递归宏观经济理论[M].第2版.杨斌等译.北京：中国人民大学出版社,2010.66-72.

[31] 刘斌.动态随机一般均衡模型及其应用[M].北京：中国金融出版社，2010.14-19.

[32] Salop S C. Monopolistic competition with outside goods[J]. Bell Journal of Economics, 1979, 10(1): 141-156.

[33] 张凯.存在水平差异化的多寡头双边平台企业竞争研究[J].运筹与管理,2013,22(2):249-255.

The Dynamic Optimal Prices of Two-sided Platform with Adaptive Expectations

ZOU Jia, GUO Li-hong, ZHANG Wei

(SchoolofEconomicsandManagement,Xi’anUniversityofTechnology,Xi’an710048,China)

We study the dynamic optimal prices of two-sided platforms which the two sides of users sequentially join and the users of firstly joining side form adaptive expectations to the quantity of the users of secondly joining side. We build up the optimum control model of two-sided market based on adaptive expectation and respectively solve the model through Euler equation and Lagrangian multiplier method in order to obtain two optimal prices sequences which differ in the types of expression in each of the monopoly and duopoly market. The two sequences, which the former one is shown as the relation between the optimal prices of the current period and the optimal prices of past periods and the later one is shown as the complete optimal prices sequence from initial period to terminal period, would respectively apply to the pricing problem of platforms under different conditions that the optimal prices of past periods are given or the time of termination is given rather than that of the past optimal prices. Finally, we simulate the numerical values of optimal prices based on the later sequence.

sequential joining; adaptive expectation; optimum control model; optimal prices sequences

2015- 05-18

国家自然科学基金资助项目(71172201)；陕西省社会科学基金资助项目(107-221450)

F224.32

A

1003-5192(2016)04- 0069- 06

10.11847/fj.35.4.69