高中数学课堂中“少教多学”教学模式的尝试

陈　昊

(四川省泸县第五中学，646105)



高中数学课堂中“少教多学”教学模式的尝试

陈昊

(四川省泸县第五中学，646105)

知识要过手才能内化为学生的东西,通过前段时间对西峡中学的“三疑三探”和洋思中学的“先学后教,当堂训练”等模式的思考,感受最深的是学生学习的积极性和参与热情度不是传统课堂能比的．作为一线老师,我们应该明白教育要培养什么样的人，国家和社会需要什么样的人,而我们实际上又培养了什么样的人,应该怎样去培养人.“少教多学”是借鉴西峡中学的“三疑三探”和洋思中学的“先学后教,当堂训练”的模式构思的.这一模式的根本点在于将课堂的主动权赋予学生,学习活动的主人由教师变为学生.摆脱传统教育的外在性和被动性,进一步激发学生的能动性和独立性,提高课堂教学效果．

全国各地都在大力提倡教育改革，为进一步发展教育实践提供了新的契机.传统教学中所采用的教学形式和枯燥、单一的教学手段无法充分调动学生的积极性和主动性，教学过程中忽视学生的主体地位，教师按照自己的节奏进行教学活动，严重阻碍了学生自主学习能力的提升.数学教育的核心是适应社会的高速发展培养具有创新能力和创新意识的人,因此，对学生进行数学创新能力的培养和训练成为数学教学的关键．在数学课堂教学过程中教师要重视对学生学习能力的培养,不断提高学生的数学实践能力，新课改更是要求在教学过程中培养学生实际动手操作能力及自主学习和合作探究的能力．要通过老师的正确引导和帮助,让学生掌握高中数学学习的基本方法,培养独立思考、独立学习的创新型学生．在数学课堂教学中通常有两种模式:一种是老师分析、讲解甚至演算解决问题；另一种是让学生思考、尝试自己解决问题.后一种模式更能让学生掌握知识,更能体现新课程理念.通过自主学习,主动探究,学生可以体验数学发展和创造的功程.以下结合自身的教学实践活动为例,对“少教多学”教学模式如何操作进行分析．

一、将“教”转化为“学”,充分利用好导学案

强调老师为主导,老师可以通过“奖励”去激发学生的学习积极性,引导学生自己去探究知识,掌握知识基础运用,这就需要老师给学生提供更多的时间和亲身参与数学活动的机会,利用好导学案.在课堂前,强化学生预习了解本节课的大体知识结构,明白本节课的重点和难点，将知识点转化为问题留给学生预习.老师在此环节需要注意导学案的编写和批改检查.在编写导学案时应注意知识的迁移,教材重点的突出以及怎样突破难点，怎样提出的问题更有效；在批改过程中老师不仅要全批全改还应做好登记，做到心中有数．在课堂教学中老师需要多提出问题,引导学生从问题入手分析知识点,归纳解题策略,从一个问题的多个角度入手,鼓励一题多探,一题多思,一题多解.学生按照老师所引导的突破口入手,思考探究与理解,通过讨论形成互补．完善知识结构总结出规律,从而显示出学生的主体地位，提高学生数学能力．在与学生的交流中，我们更应该问的是“为什么”而不是“有没有听懂”．

在这个环节,导学案的编写十分重要.比如在编写“二元一次不等式与平面区域”这一节导学案时,将学生判断平面区域的过程作为本节内容的重点.为了突出重点，可设置以下几个问题:

(1)在平面直角坐标系中,怎样判断一个点在直线的上方或下方?

(2)如何判断点P的坐标是否为不等式的解?

(3)是否与点P同侧的点的坐标都满足不等式?

(4)思考另一侧的点的坐标是否满足不等式?

前3个问题层层递进,螺旋上升，目的在于由易到难突破思维的局限性．第4个问题有两层意思：一是让学生学会用辩证的思维处理问题,体会数学的严谨性；二是为学生提供展示的机会,因为该问题可由第3个问题类比迁移得到．

二、分层教学,上好每一个学生都能听懂的数学课

经常听到老师吐槽“上课没人听”.需要思考为什么没人听,其实学生上课不听的原因很简单,是因为他们听不懂,毫无疑问每个同学都希望自己能听懂.我们的做法是：针对班级有每次能考120多分的,也有考20多分的,安排分层教学,将学生分为A、B、C三档.A等生是在数学方面总体基础知识扎实,分析解决问题能力、自主学习能力较强,学习态度端正，成绩稳定；B等生是在基础知识方面比较扎实,计算环节较弱,成绩不够稳定,需要老师督促学习；C等生是在数学方面总体能力欠缺的人.通过安排学科座位,将A等生和C等生随机安排在若干小组,每探究一个问题或知识结构,由C等生展示,B等生评价补充,A等生归纳总结，从而达到人人参与数学,人人收获数学.所以分层教学的前提是对学生分层,而分层的目的是为了人人都能进步,学生可以各尽其能,各有收获．

三、给课堂探究环节留足时间

从教育理论上来说教师是课堂的“主导”、学生是课堂的“主体”.但传统的数学课堂中,通常由老师掌控,教师满堂灌,不停地问“懂了没?有没有问题?”没有给学生思考的机会和时间,甚至还会利用课余时间传授理论知识,害怕没有讲到某个知识点或细节.数学教学的规律在于学生逐步地将外在形式的教学活动演化为内在思维,由旧知识迁移新知识,用新知识内化旧知识,形成系统．应该重视学生探究思考这个过程,向学生提供探究的资料或问题,督促学生利用课余时间动脑思考,然后小组进行合作探究,让学生自己发现问题、探讨问题、解决问题并进行展示.这样可以创新学生的解题方法,提高学生的解题能力和思维水平,从而可以达到让学生共同进步的目的．

四、有效反思,活用解题理论

高中生必然要面对高考,应对高考必须学会解题.学会解题既需要老师适时的引导更需要解题经验的积累,这就要求老师积累大量的解题策略和解题理论，以便引导学生正确解题．波利亚将解决数学问题归结为四个阶段:弄清问题——拟定计划——实现计划——回顾解答．我们解题教学却是重视“实现计划”阶段忽略了“拟定计划”和“回顾解答”阶段．“拟定计划”是培养学生分析问题能力和探究意识不可缺少的过程,而“回顾解答”引导学生进行反思、总结、拓展是开发元认知的重要过程，而元认知的开发是生成解题智慧的必要条件.罗增儒教授认为解题分析是思维过程的暴露,是一个不断暴露解题过程、循环提升理解能力的探究活动,在过程中既有思路探求的暴露也有结果反思的暴露．在思维上,既有数学家的思维也包括了老师和学生的思维,所以要特别重视个例研究．他还提出了“通过有限道题的学习去顿悟那种解无限道题的数学机智”.每个问题都可以总结,每个知识点都可以整合.新思想的产生一般不遵循逻辑的规律,而常常是突发地、偶然地、整体地出现．要注意有效的反思,适时的反思孕育解题方法．

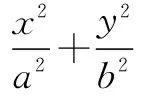
解法1在解这道几何题时首先可以考虑将几何问题转化为代数问题.设点P(x0,y0)，则可以得到

从而可得

4a2b2-3a2c2=c4-4b2c2+4b4,

解法2利用几何关系设中点为M,OM为∆F2PF的中位线，于是得到PF2=2b,满足勾股定理:

(a-b)2+b2=c2,

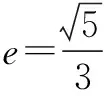
此题找准几何关系后容易解答,但部分同学根据经验容易采用常规解答，运算量大，耗费时间．所以,回顾解答,有效反思,我们可以从一个题的学习顿悟出解一类题的思想方法,提高课堂效率．

五、鼓励学生提出自己的想法,开发元认知

元认知是美国心理学家弗拉维尔在1976年提出的.元认知就是对认知的认知,是个人对自己的认知加工过程的自我觉察、自我评价、自我调节.一个元认知能力强的人在认知活动中会表现出高度的自觉性,能够根据自己的认知结构的特点以及当前的问题情境,恰当地选择思维方法和策略,从而提高自己认知活动的效果．提倡学生一题多解、一题多用、一题多探、一题多变、一题多引,鼓励学生提出自己的想法和认识,然后大家进行讨论、检验并内化为自己的知识．

“少教多学”是教育改革下产生的创新性教学模式.一方面能充分调动起学生学习的积极性；另一方面能够充分发挥学生学习的主动性,提高自主学习的能力，进而加强对数学认识的理解,全面提高数学教学的结果．应当看到，教育改革任重道远,需要且行且思且试验．